当前位置： 首页 > news >正文

【Unity的 Built-in 渲染管线下实现好用的GUI模糊效果_Blur_案例分享(内附源码)】

news 2026/2/8 8:43:56

CGPROGRAM实现好用的GUI模糊效果

  • 实现Blur模糊方式1
    • C#代码如下
    • 方式1_Shader代码如下
  • 实现Blur模糊方式2
    • 方式2_Shader如下

实现Blur模糊方式1

其他的模糊效果，在这一篇。

效果如图：
在这里插入图片描述

新建一个C#文件，命名为"CommandBlur"，打开C#，删除内容，复制粘贴下面的代码：

C#代码如下

using UnityEngine;
using Unit

相关文章：

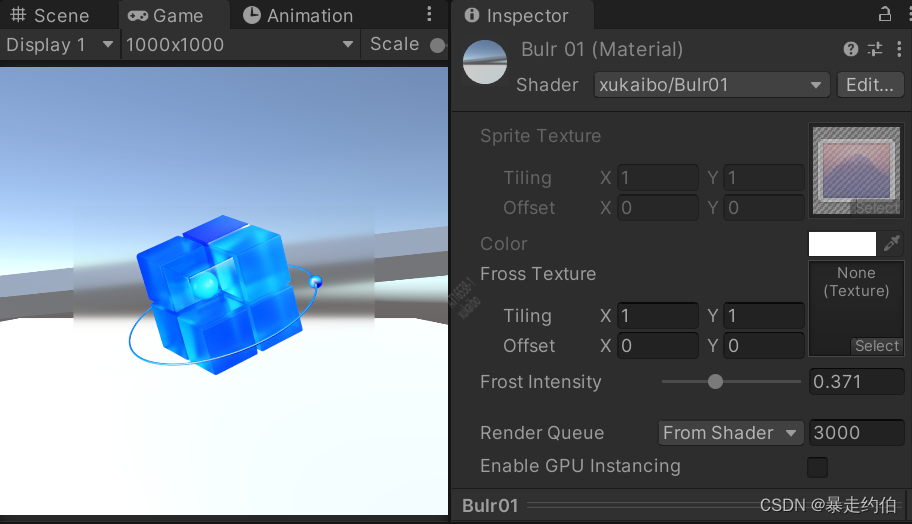
【Unity的 Built-in 渲染管线下实现好用的GUI模糊效果_Blur_案例分享(内附源码)】

CGPROGRAM实现好用的GUI模糊效果 实现Blur模糊方式1C#代码如下方式1_Shader代码如下实现Blur模糊方式2方式2_Shader如下实现Blur模糊方式1 其他的模糊效果，在这一篇。 效果如图： 新建一个C#文件，命名为"CommandBlur"，打开C#，删除内容，复制粘贴下面的代码：…...

编程日记 2023/9/30 13:42:34

AR智能眼镜：提升现场服务技能、效率与盈利能力的利器（一）

随着技术的不断进步，现场服务组织正朝着远程支持转变，用以解决技能差距和生产力问题，提高员工培训和操作效率，同时为企业提高利润率，创造竞争优势。 本文将探讨增强现实（AR）、辅助现实&#xf…...

编程日记 2023/9/30 13:41:33

ChatGPT 在机器学习中的应用

办公室里一个机器人坐在人类旁边，Artstation 上的流行趋势，美丽的色彩，4k，充满活力，蓝色和黄色， DreamStudio出品 一、介绍 大家都知道ChatGPT。它在解释机器学习和深度学习概念方面也非常高效，…...

编程日记 2023/9/30 13:40:32

【JavaEE】锁策略

文章目录 前言1. 乐观锁和悲观锁2. 重量级锁和轻量级锁3. 自旋锁和挂起等待锁4. 公平锁和非公平锁5. 可重入锁和非可重入锁6. 读写锁Java synchronized 分别对应哪些锁策略1. 乐观锁和悲观锁2. 重量级锁和轻量级锁3. 自旋锁和挂起等待锁4. 公平锁和非公平锁5. 可重入锁和非可重…...

编程日记 2023/9/30 13:37:30

在 SDXL 上用 T2I-Adapter 实现高效可控的文生图

T2I-Adapter 是一种高效的即插即用模型，其能对冻结的预训练大型文生图模型提供额外引导。T2I-Adapter 将 T2I 模型中的内部知识与外部控制信号结合起来。我们可以根据不同的情况训练各种适配器，实现丰富的控制和编辑效果。 同期的 ControlNet 也有类似的…...

编程日记 2023/9/30 13:33:25

Python分支结构和循环结构

嗨喽~大家好呀，这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 一.分支结构 分支结构是根据判断条件结果而选择不同向前路径的运行方式，分支结构分为：单分支，二分支和多分支。 1&#xff0…...

编程日记 2023/9/30 13:32:24

Unity调用API函数对系统桌面和窗口截图

Unity3D调用WINAPI函数对系统窗口截图 引入WINAPI函数调用WINAPI函数进行截图使用例子 引入WINAPI函数 using System; using System.Collections; using System.Runtime.InteropServices; using System.Drawing;[DllImport("user32.dll")]private static extern Int…...

编程日记 2023/9/30 13:29:22

【问题思考总结】CPU怎么访问磁盘？CPU只有32位，最多只能访问4GB的空间吗？

问题 在学习操作系统的时候发现了这样一个问题，32位的CPU寻址空间只有4GB，难道只有4GB的空间可以使用吗？以此为始，我开始了一些思考。 思考 Q1：首先，我似乎混淆了一个概念，内存和外存&#x…...

编程日记 2023/9/30 13:27:20

UG NX二次开发(C++)-CAM-根据刀具对程序组进行重新分组

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 1、前言2、在UG NX中创建一个三维模型3、在UG NX/CAM中创建多个加工程序4、采用UG NX二次开发（NXOpen）实现按照刀具分组程序组4.2 创建UI Styler4.1 实现逻辑4.2 生成的代码如下：4.3 测试效果4.…...

编程日记 2023/9/30 13:23:17

Unity如何实现TreeView

前言 最近有一个需求，需要实现一个TreeView的试图显示，开始我一直觉得这么通用的结构，肯定有现成的UI组件或者插件可以使用，结果，找了好久，都没有找到合适的插件，有两个效果差强人意。 最后在回家的路上突然灵光一闪，想到了一种简单的实现方式，什么插件都不用，仅使用…...

编程日记 2023/9/30 13:22:16

Android widget 小部件使用指南强化版

Android widget 小部件使用指南强化版 一、简单UI的小部件二、含集合的小部件三、可配置的小部件四、可控制的小部件五、Android 12 Widget 更新 小部件是主屏幕定制的一个重要方面。您可以将它们视为应用程序最重要的数据和功能的“概览”视图，这些数据和功能可以直…...

编程日记 2023/9/30 13:21:15

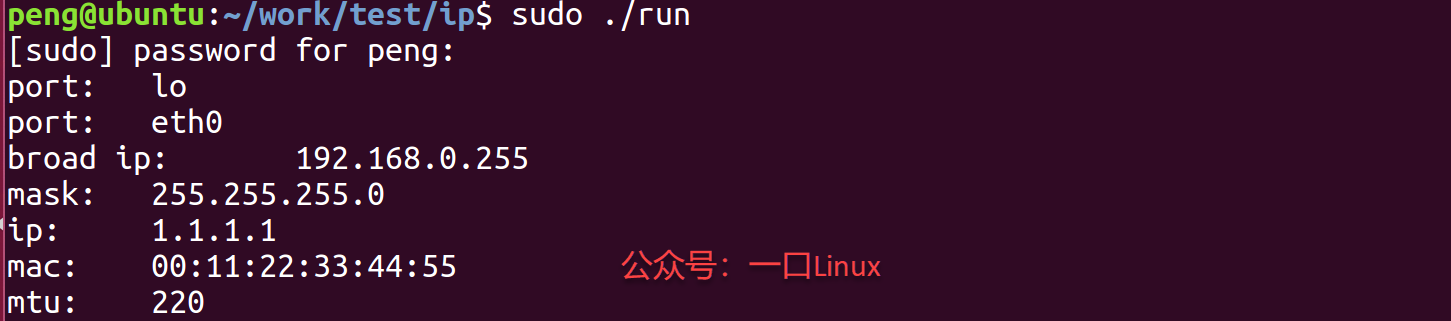
Linux下C语言操作网卡的几个代码实例？特别实用

前面写了一篇关于网络相关的文章：如何获取当前可用网口。 《简简单单教你如何用C语言列举当前所有网口！》 那么如何使用C语言直接操作网口？ 比如读写IP地址、读写MAC地址等。 一、原理 主要通过系统用socket()、ioctl()、实现 int sock…...

编程日记 2023/9/30 13:18:12

noip2011选择旅馆

1.审题：第一个人与第二个人入住的旅馆要求是同色的； 两个人去消费的旅馆并没有要求与入住的旅馆是同色的（这点要小心） 2.要求记录以下数据： 1）a[color]表示当前同为颜色color的旅馆数 2）b[co…...

编程日记 2023/9/30 13:16:10

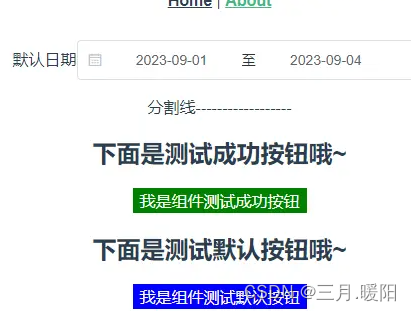
vue造轮子完整指南--npm组件包开发步骤

一、项目包文件的创建和初始化。 1. 新建项目包。 vue create <Project Name> //用于发布npm包的项目文件名 ps:一般选择自定义&#xff0c;然后不需要Vuex和Router&#xff0c;其他选项按自己实际情况选择安装即可。 2.修改原始src文件名、新增组件项目存放文件和修改…...

编程日记 2023/9/30 13:14:09

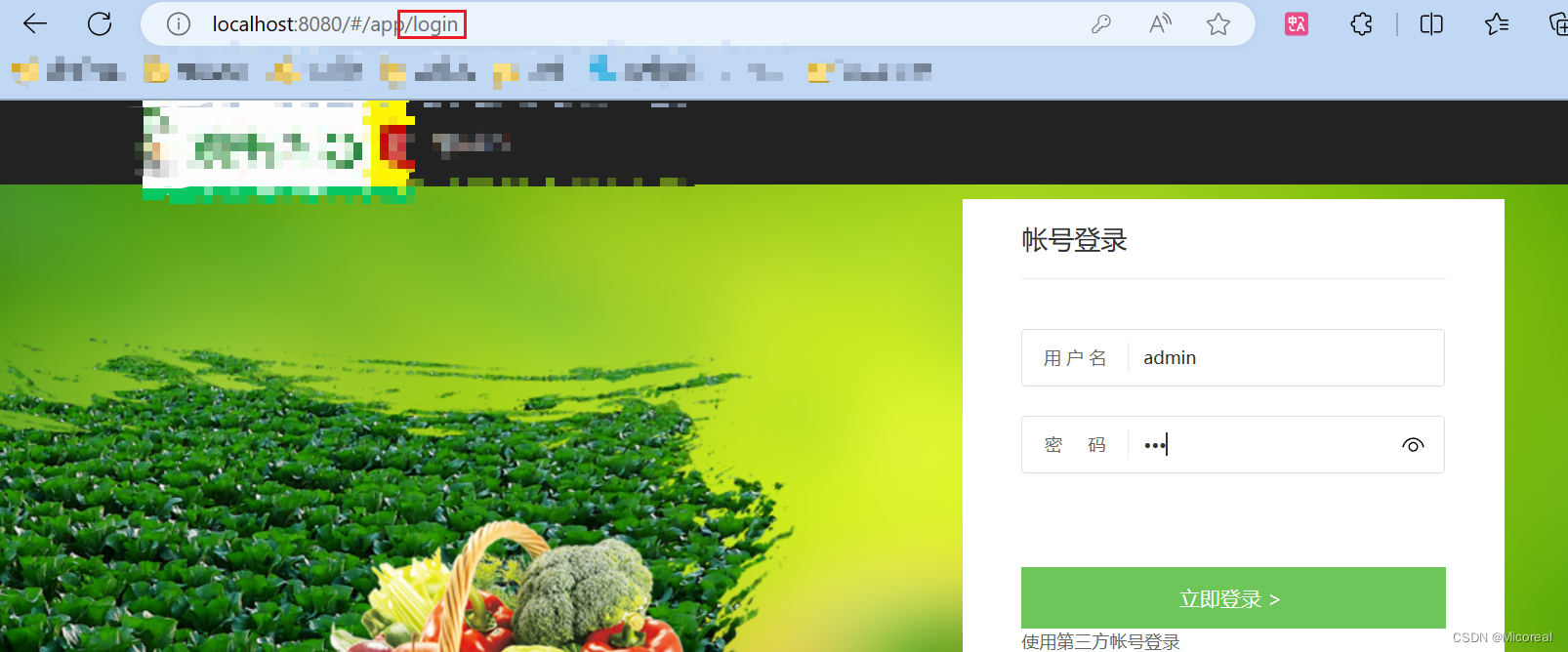
28 drf-Vue个人向总结-1

文章目录 前后端分离开发展示项目项补充知识开发问题浏览器解决跨域问题 drf 小tips设置资源root目录使用自定义的user表设置资源路径media数据库补充删除表中数据单页面与多页面模式过滤多层自关联后端提交的数据到底是什么jwt token登录设置普通的 token 原理使用流程解析 jw…...

编程日记 2023/9/30 13:06:01

线性代数(七) 矩阵分析

前言 从性线变换我们得出&#xff0c;矩阵和函数是密不可分的。如何用函数的思维来分析矩阵。 矩阵的序列 通过这个定义我们就定义了矩阵序列的收敛性。 研究矩阵序列收敛性的常用方法&#xff0c;是用《常见向量范数和矩阵范数》来研究矩阵序列的极限。 长度是范数的一个特…...

编程日记 2023/9/30 13:02:58

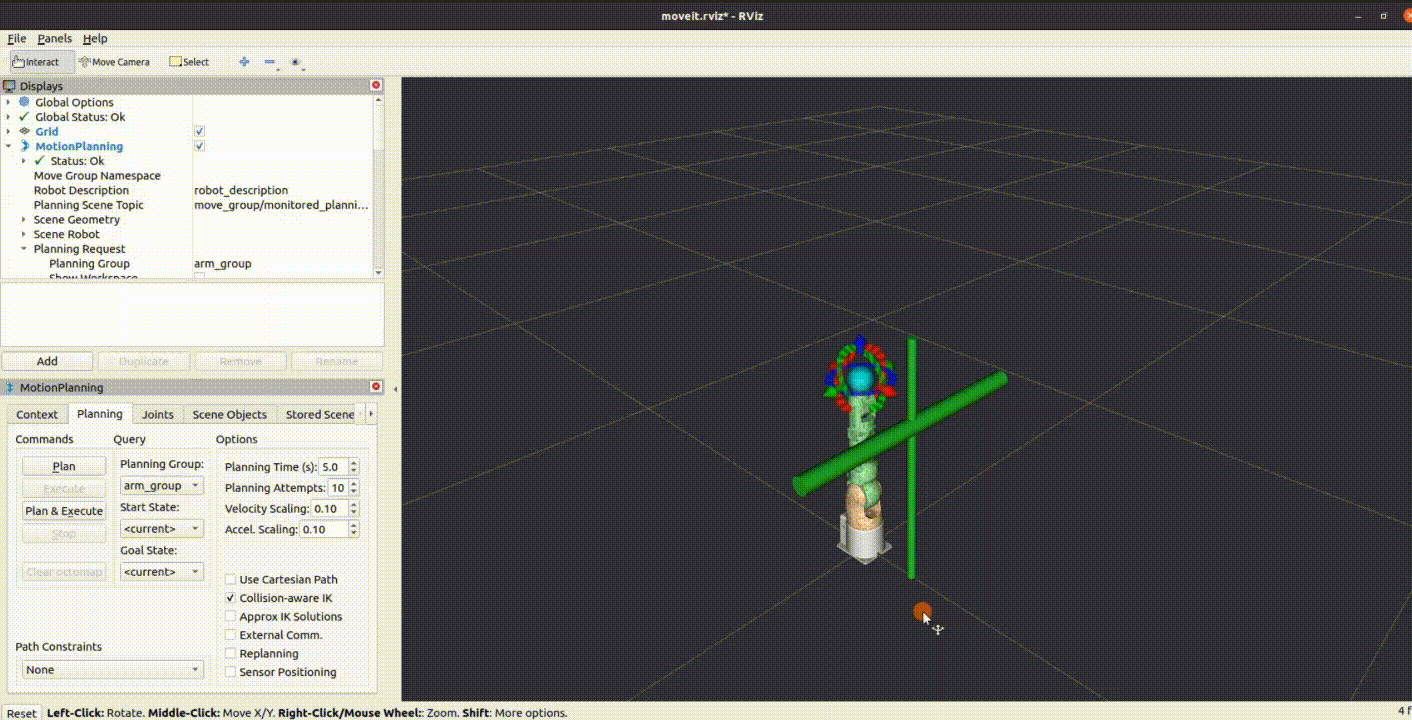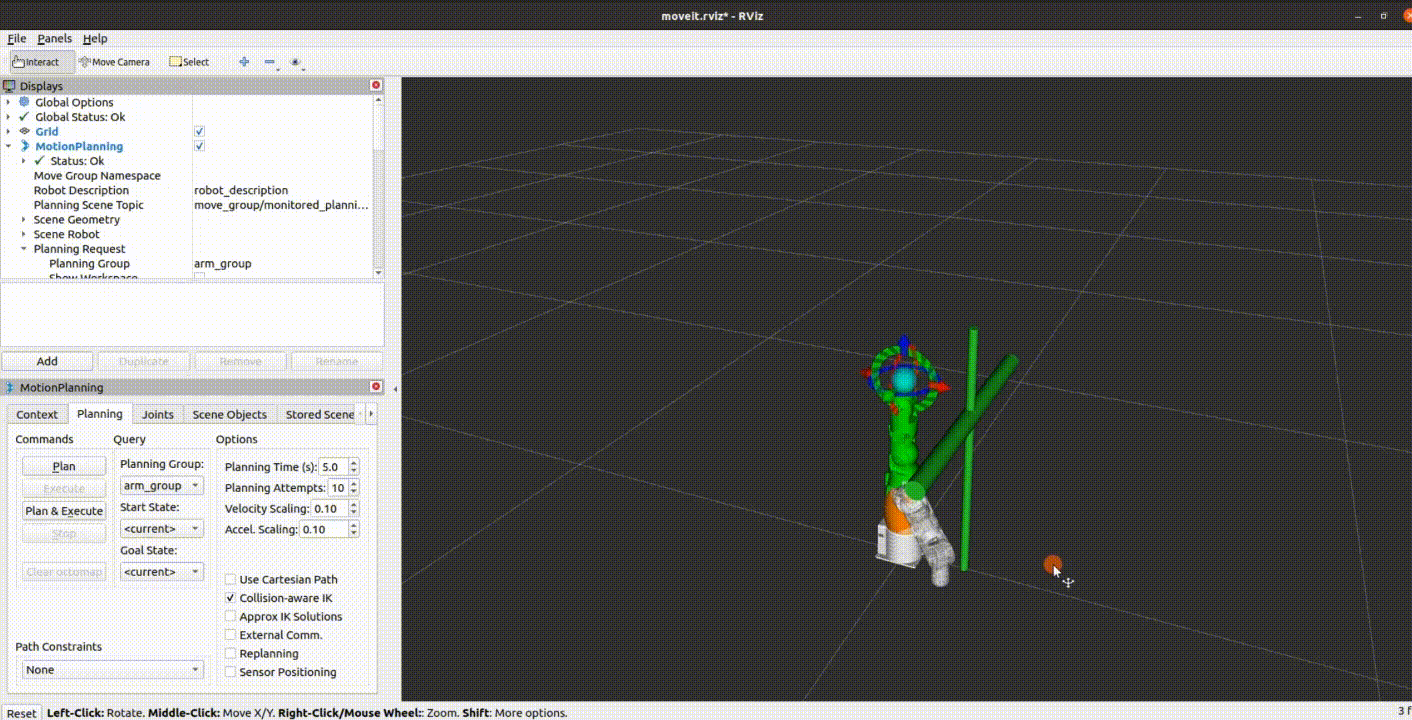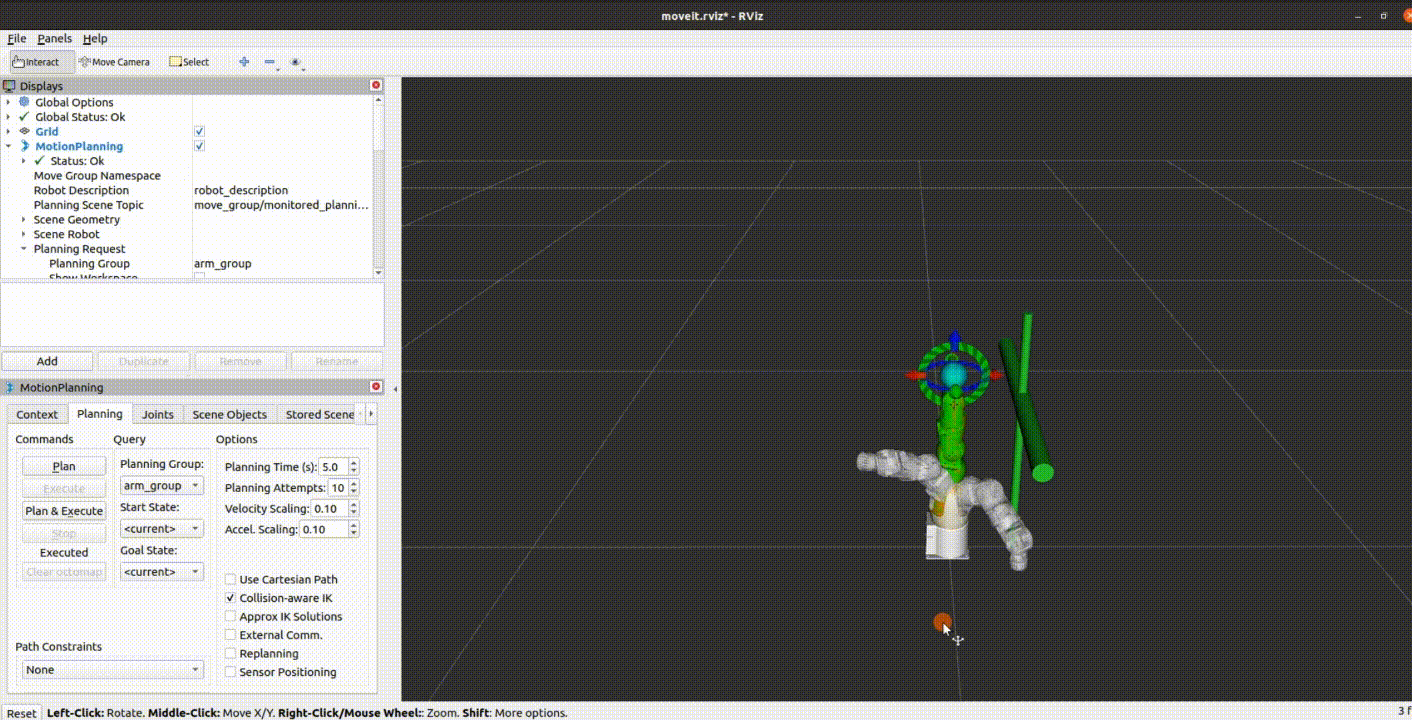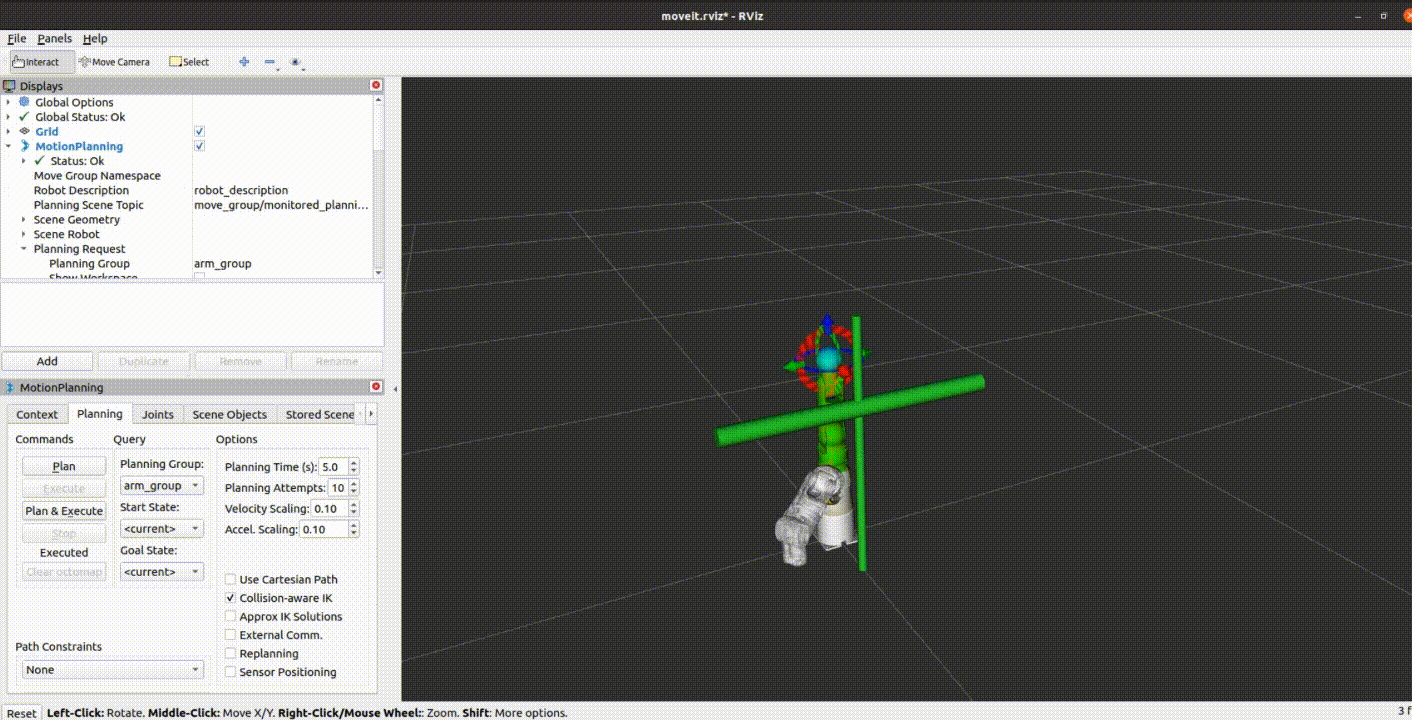
myArm 全新七轴桌面型机械臂

引言 在不断演进的科技世界中&#xff0c;我们始终追求创新和卓越&#xff0c;以满足客户的需求并超越他们的期望。今天&#xff0c;我们很高兴地宣布我们的最新产品——myArm 300 Pi&#xff0c;一款七轴的桌面型机械臂。这款产品的独特之处在于其灵活性和可编程性&#xff0c…...

编程日记 2023/9/30 12:59:54

tomcat乱码解决

解决乱码 1、修改bin\catalina.bat配置文件 修改tomcat的配置文件&#xff0c;找到tomcat路径下的\bin目录下的catalina.bat文件&#xff0c;修改 set “JAVA_OPTS%JAVA_OPTS% %JSSE_OPTS% -Dfile.encodingUTF-8 -Dsun.jnu.encodingUTF-8 ” 2、修改conf\logging.properties配置…...

编程日记 2023/9/30 12:57:52

【Linux】详解线程第三篇——线程同步和生产消费者模型

线程同步和生消模型 前言正式开始再次用黄牛抢票来讲解线程同步的思想通过条件变量来实现线程同步条件变量接口介绍初始化和销毁pthread_cond_waitsignal和broadcast 生产消费者模型三种关系用基本工程师思维再次理解基于生产消费者模型的阻塞队列版本一版本二多生多消 利用RAI…...

编程日记 2023/9/30 12:56:51

k8s 安装

文章目录 k8s 客户端安装k8s集群minikubekindkubeadm 验证 k8s 客户端 用于连接k8s集群&#xff0c;建议下载1.23.x的版本&#xff0c;其他的版本本地运行可能会有莫名其妙的报错 https://dl.k8s.io/release/v1.23.16/bin/linux/amd64/kubectl 安装k8s集群 minikube Minik…...

编程日记 2023/9/30 12:55:50

汽车生产虚拟实训中的技能提升与生产优化​

在制造业蓬勃发展的大背景下&#xff0c;虚拟教学实训宛如一颗璀璨的新星&#xff0c;正发挥着不可或缺且日益凸显的关键作用&#xff0c;源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例&#xff0c;汽车生产线上各类…...

编程新知 2026/1/27 7:46:36

蓝牙 BLE 扫描面试题大全(2)：进阶面试题与实战演练

前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1)&#xff1a;从基础到实战的深度解析-CSDN博客&#xff0c;但实际面试中&#xff0c;企业更关注候选人对复杂场景的应对能力&#xff08;如多设备并发扫描、低功耗与高发现率的平衡&#xff09;和前沿技术的…...

编程新知 2026/2/5 3:41:42

页面渲染流程与性能优化

页面渲染流程与性能优化详解&#xff08;完整版&#xff09; 一、现代浏览器渲染流程&#xff08;详细说明&#xff09; 1. 构建DOM树 浏览器接收到HTML文档后&#xff0c;会逐步解析并构建DOM&#xff08;Document Object Model&#xff09;树。具体过程如下&#xff1a; (…...

编程新知 2026/1/31 11:58:35

跨链模式：多链互操作架构与性能扩展方案

跨链模式&#xff1a;多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈&#xff1a;模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展&#xff08;H2Cross架构&#xff09;&#xff1a; 适配层&#xf…...

编程新知 2026/2/5 14:15:13

从零实现STL哈希容器：unordered_map/unordered_set封装详解

本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说&#xff0c;直接开始吧&#xff01; 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

编程新知 2026/1/31 12:47:25

Unit 1 深度强化学习简介

Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库&#xff0c;例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体&#xff0c;比如 SnowballFight、Huggy the Do…...

编程新知 2025/9/18 1:39:03

根据万维钢·精英日课6的内容，使用AI（2025）可以参考以下方法：

根据万维钢精英日课6的内容&#xff0c;使用AI&#xff08;2025&#xff09;可以参考以下方法&#xff1a; 四个洞见 模型已经比人聪明&#xff1a;以ChatGPT o3为代表的AI非常强大&#xff0c;能运用高级理论解释道理、引用最新学术论文&#xff0c;生成对顶尖科学家都有用的…...

编程新知 2026/1/10 1:08:51

C++八股 —— 单例模式

文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全&#xff08;Thread Safety&#xff09; 线程安全是指在多线程环境下&#xff0c;某个函数、类或代码片段能够被多个线程同时调用时&#xff0c;仍能保证数据的一致性和逻辑的正确性&#xf…...

编程新知 2025/12/2 3:35:50

docker 部署发现spring.profiles.active 问题

报错&#xff1a; org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

编程新知 2025/9/20 12:14:18

算法笔记2

1.字符串拼接最好用StringBuilder&#xff0c;不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

编程新知 2026/1/27 12:17:05