排序:基数排序算法分析
1.算法思想
假设长度为n的线性表中每个结点aj的关键字由d元组 ( k j d − 1 , k j d − 2 , k j d − 3 , . . . , k j 1 , k j 0 ) (k_{j}^{d-1},k_{j}^{d-2},k_{j}^{d-3},... ,k_{j}^{1} ,k_{j}^{0}) (kjd−1,kjd−2,kjd−3,...,kj1,kj0)组成,
其中, 0 < = k j i < = r − 1 ( 0 < = j < n , 0 < = i < = d − 1 ) 0<=k_{j}^{i}<=r-1(0<=j<n,0<=i<=d-1) 0<=kji<=r−1(0<=j<n,0<=i<=d−1),r称为“基数”。
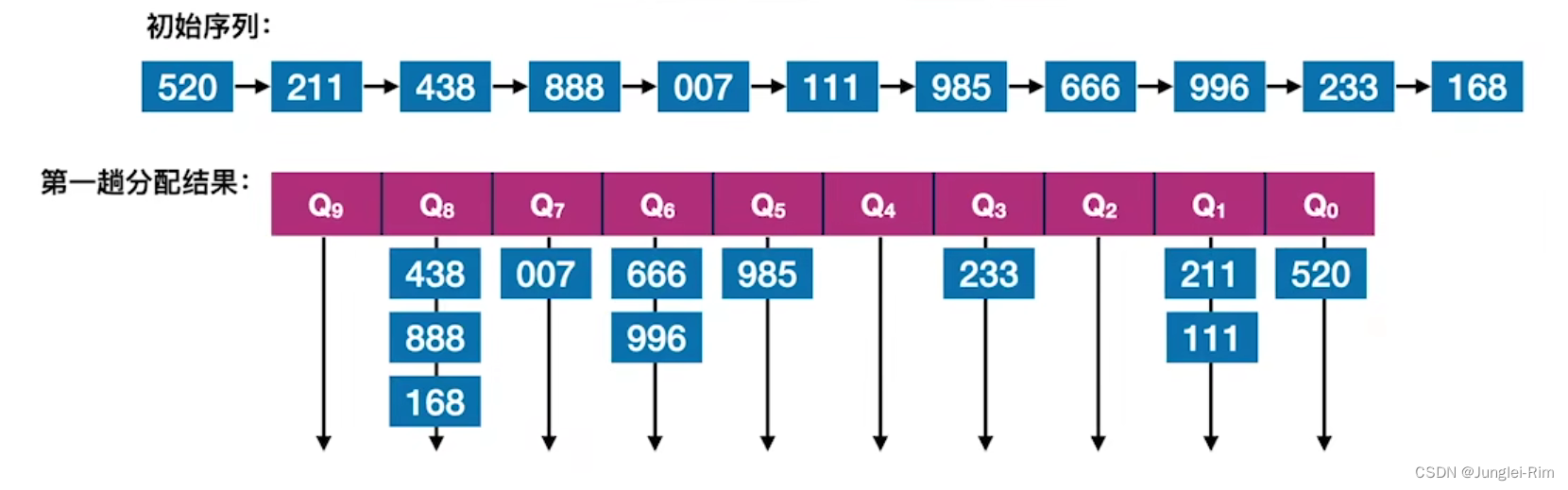
基数排序得到递减序列的过程如下:
- 初始化︰设置r个空队列, Q r − 1 , Q r − 2 , . . . , Q 0 Q_{r-1},Q_{r-2,}...,Q_0 Qr−1,Qr−2,...,Q0
- 按照各个关键字位权重递增的次序(个、十、百),对d个关键字位分别做“分配”和“收集”
- 分配:顺序扫描各个元素,若当前处理的关键字位,则将元素插入Qx队尾,一趟分配耗时O(n)
- 收集:把 Q r − 1 , Q r − 2 , . . . , Q 0 Q_{r-1},Q_{r-2},...,Q_0 Qr−1,Qr−2,...,Q0各个队列中的结点依次出队并链接,一趟收集耗时O(r)
例如:收集:得到一个按“百位”递减排列的序列,若“百位”相同则按“十位"递减排列,若“十位”还相同则按“个位”递减排列。
基数排序不是基于“比较”的排序算法。
2.算法效率分析
基数排序通常基于链式存储实现:
typedef struct LinkNode {ElemType data;struct LinkNode *next;
} LinkNode, *LinkList;
链式队列设计:
typedef struct {//链式队列LinkNode *front, *rear;//队列的队头和队尾指针
} LinkQueue;
1.空间复杂度
需要r个辅助队列,空间复杂度= O(r)。
2.时间复杂度
一趟分配O(n),一趟收集O(r),总共d趟分配、收集,总的时间复杂度=O(d(n+r))
3.稳定性
基数排序是稳定的。
3.基数排序的应用
1.学生年龄排序
某学校有10000学生,将学生信息按年龄递减排序
生日可拆分为三组关键字:年(1991-2005)、月(1-12)、日(1-31)
权重:年>月>日,年、月、日越大,年龄越小。
- 第一趟分配、收集(按“日"递增)
- 第二趟分配、收集(按“月”递增)
- 第三趟分配、收集(按“年”递增)
若采用基数排序,时间复杂度= O(d(n+r)),约等于 O(30000)
若采用 O ( n 2 ) O(n^2) O(n2)的排序,约等于 O ( 1 0 8 ) O(10^8) O(108)
若采用 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)的排序,约等于O(140000)
可以看到这里采用基数排序时间复杂度会更低。
2.基数排序适合解决的问题
- ①数据元素的关键字可以方便地拆分为d组,且d较小(反例:给5个人的身份证号排序)
- ②每组关键字的取值范围不大,即r较小(反例:给中文人名排序)
- ③数据元素个数n较大(擅长:给十亿人的身份证号排序)
相关文章:

排序:基数排序算法分析
1.算法思想 假设长度为n的线性表中每个结点aj的关键字由d元组 ( k j d − 1 , k j d − 2 , k j d − 3 , . . . , k j 1 , k j 0 ) (k_{j}^{d-1},k_{j}^{d-2},k_{j}^{d-3},... ,k_{j}^{1} ,k_{j}^{0}) (kjd−1,kjd−2,kjd−3,...,kj1,kj0)组成, 其中&am…...
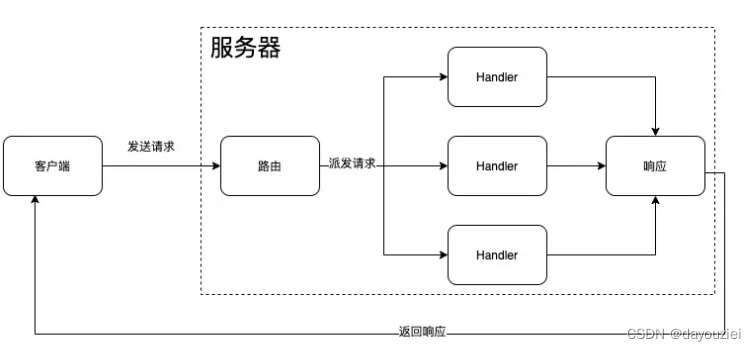
用go实现http服务端和请求端
一、概述 本文旨在学习记录下如何用go实现建立一个http服务器,同时构造一个专用格式的http客户端。 二、代码实现 2.1 构造http服务端 1、http服务处理流程 基于HTTP构建的服务标准模型包括两个端,客户端(Client)和服务端(Server)。HTTP 请求从客户端…...

幂级数和幂级数的和函数有什么关系?
幂级数和幂级数的和函数有什么关系? 本文例子引用自:80_1幂级数运算,逐项积分、求导【小元老师】高等数学,考研数学 求幂级数 ∑ n 1 ∞ 1 n x n \sum\limits_{n1}^{\infty}\frac{1}{n}x^n n1∑∞n1xn 的和函数 ÿ…...

Git多账号管理通过ssh 公钥的方式,git,gitlab,gitee
按照目前国内访问git,如果不科学上网,我们很大可能访问会超时。基于这个,所以我现在的git 配置已经增加到了3个了 一个公司gitlab,一个git,一个gitee. 以下基于这个环境,我们来说明下如何创建配置ssh公钥。…...

在nodejs常见的不良做法及其优化解决方案
在nodejs常见的不良做法及其优化解决方案 当涉及到在express和nodejs中开发应用程序时。遵循最佳实践对于确保项目的健壮性、可维护性和安全性至关重要。 在本文中,我们将探索开发人员经常遇到的几种常见的错误做法,并通过代码示例研究优化的最佳做法&…...

关于layui upload上传组件上传文件无反应的问题
最近使用layui upload组件时,碰到了上传文件无反应的问题,感到非常困惑。 因为使用layui upload组件不是一次两次了,之前每次都可以,这次使用同样的配方,同样的姿势,为什么就不行了呢? 照例先…...

容器网络之Flannel
第一个问题位置变化,往往是通过一个称为注册中心的地方统一管理的,这个是应用自己做的。当一个应用启动的时候,将自己所在环境的 IP 地址和端口,注册到注册中心指挥部,这样其他的应用请求它的时候,到指挥…...
:如何进行乳腺癌检测?)
SVM(下):如何进行乳腺癌检测?
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。 🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、…...

嵌入式Linux应用开发-第十五章具体单板的按键驱动程序
嵌入式Linux应用开发-第十五章具体单板的按键驱动程序 第十五章 具体单板的按键驱动程序(查询方式)15.1 GPIO操作回顾15.2 AM335X的按键驱动程序(查询方式)15.2.1 先看原理图确定引脚及操作方法15.2.2 再看芯片手册确定寄存器及操作方法15.2.3 编程15.2.3.1 程序框架15.2.3.2 硬…...
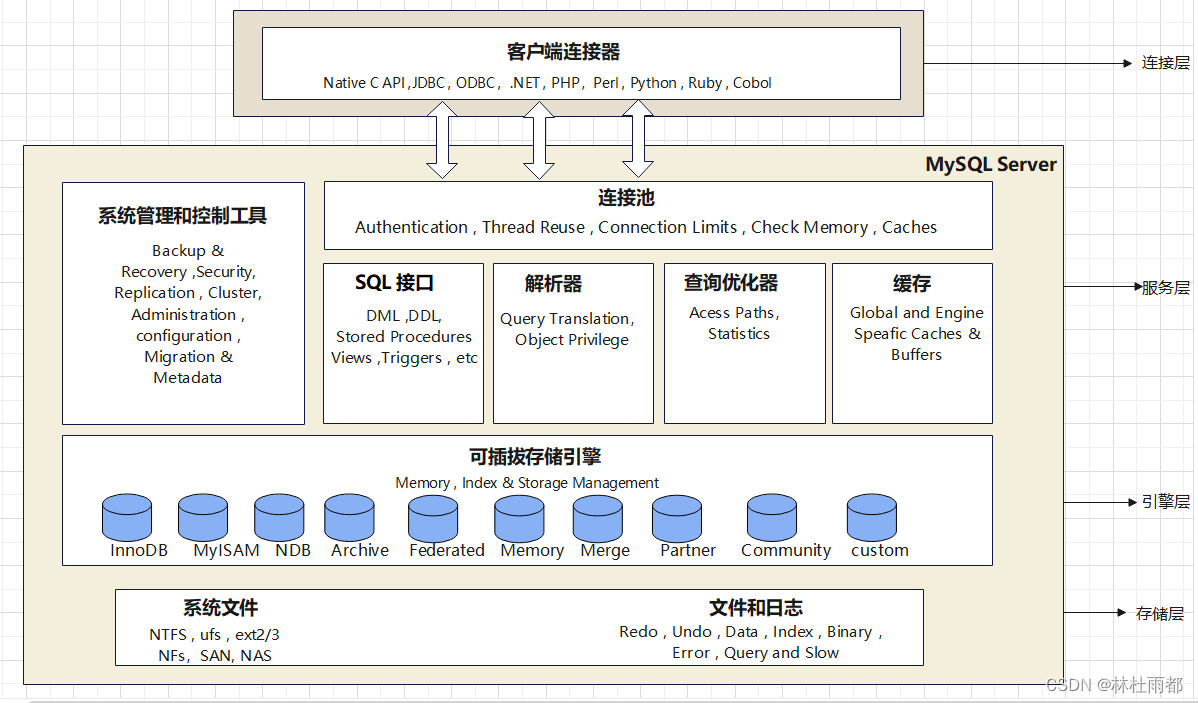
MySQL体系结构和四层架构介绍
MySQL体系结构图如下: 四层介绍 1. 连接层: 它的主要功能是处理客户端与MySQL服务器之间的连接(比如Java应用程序通过JDBC连接MySQL)。当客户端应用程序连接到MySQL服务器时,连接层对用户进行身份验证、建立安全连接并管理会话状态。它还处理…...

【产品运营】如何做好B端产品规划
产品规划是基于当下掌握的多维度信息,为追求特定目的,而制定的产品资源投入计划。 产品规划是基于当下掌握的多维度信息(客户需求、市场趋势、竞争对手、竞争策略等),为追求特定目的(商业增长、客户满意等&…...

ruoyi-启动
1 springboot 版本 git 地址 ruoyi-vue-pro: 🔥 官方推荐 🔥 RuoYi-Vue 全新 Pro 版本,优化重构所有功能。基于 Spring Boot MyBatis Plus Vue & Element 实现的后台管理系统 微信小程序,支持 RBAC 动态权限、数据权限…...
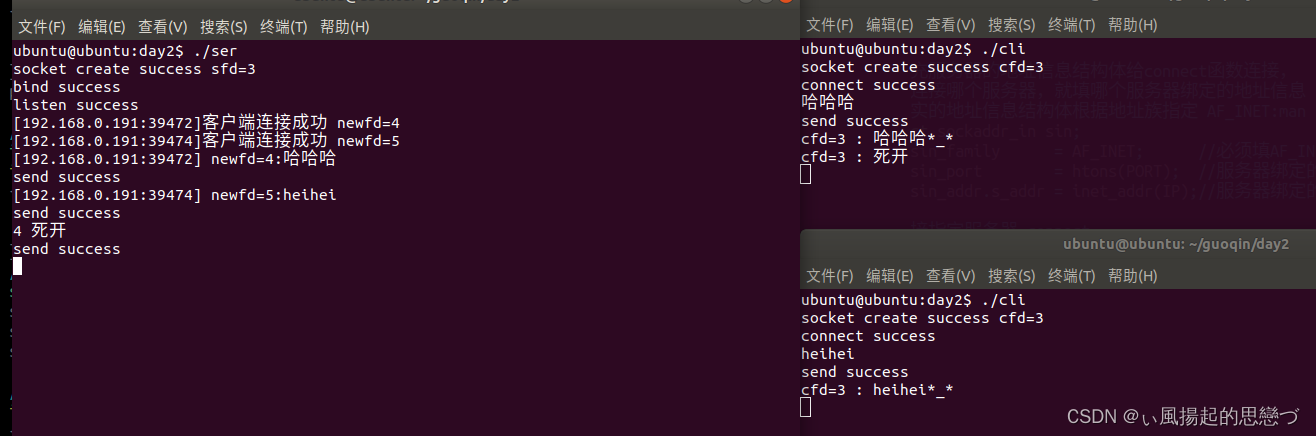
select完成服务器并发
服务器 #include <myhead.h>#define PORT 4399 //端口号 #define IP "192.168.0.191"//IP地址//键盘输入事件 int keybord_events(fd_set readfds); //客户端交互事件 int cliRcvSnd_events(int , struct sockaddr_in*, fd_set *, int *); //客户端连接事件 …...
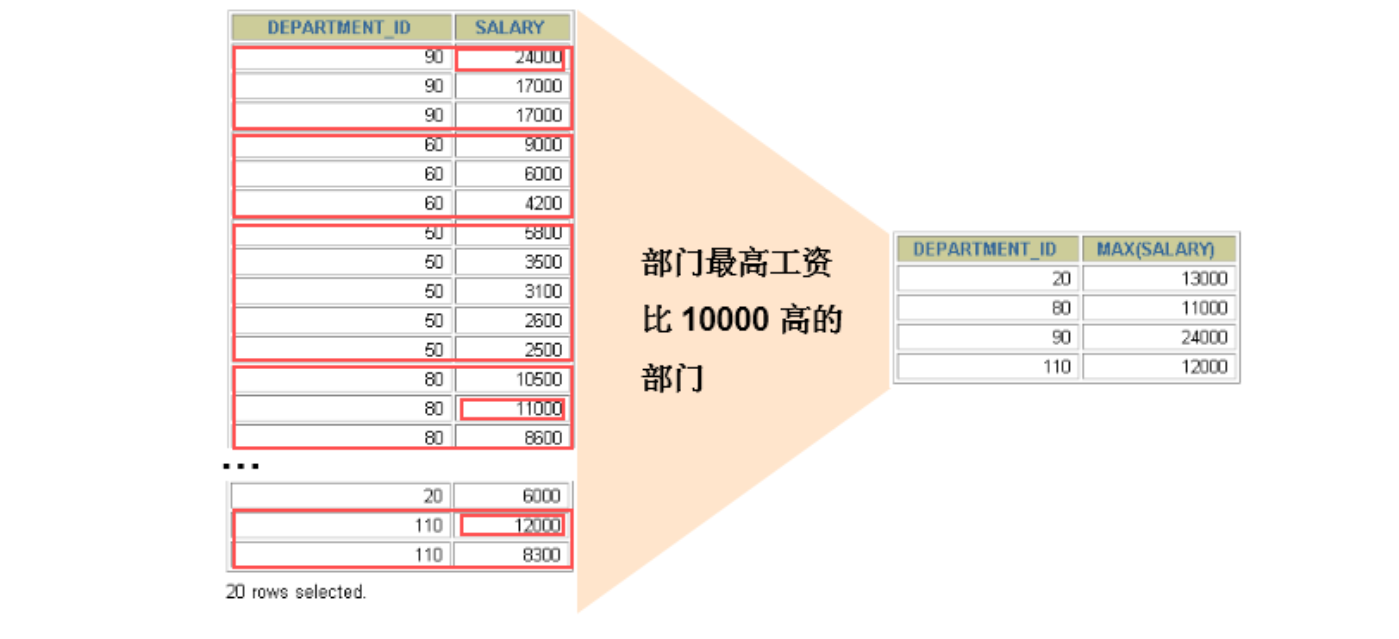
初级篇—第四章聚合函数
文章目录 聚合函数介绍聚合函数介绍COUNT函数AVG和SUM函数MIN和MAX函数 GROUP BY语法基本使用使用多个列分组WITH ROLLUP HAVING基本使用WHERE和HAVING的对比开发中的选择 SELECT的执行过程查询的结构SQL 的执行原理 练习流程函数 聚合函数介绍 聚合函数作用于一组数据&#x…...
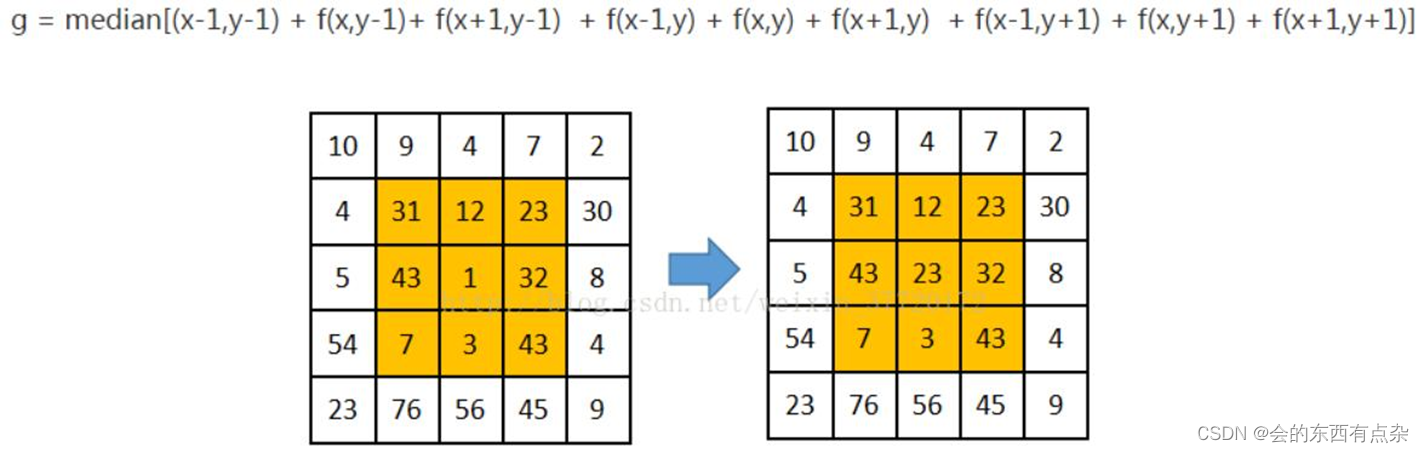
计算机图像处理-中值滤波
非线性滤波 非线性滤波是利用原始图像跟模版之间的一种逻辑关系得到结果,常用的非线性滤波方法有中值滤波和高斯双边滤波,分别对应cv2.medianBlur(src, ksize)方法和cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]])方法。 …...

Golang中的包和模块设计
Go,也被称为Golang,是一种静态类型、编译型语言,因其简洁性和对并发编程的强大支持而受到开发者们的喜爱。Go编程的一个关键方面是其包和模块系统,它允许创建可重用、可维护和高效的代码。本博客文章将深入探讨在Go中设计包和模块…...
web:[极客大挑战 2019]Upload
题目 页面显示为一个上传,猜测上传一句话木马文件 先查看源代码看一下有没有有用的信息,说明要先上传图片,先尝试上传含有一句话木马的图片 构造payload <?php eval($_POST[123]);?> 上传后页面显示为,不能包含<&…...
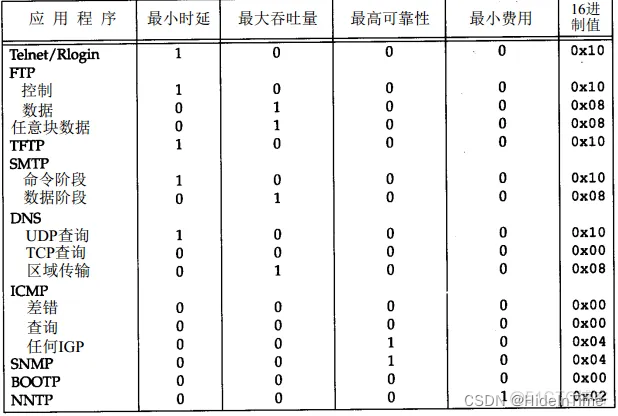
ICMP差错包
ICMP报文分类 Type Code 描述 查询/差错 0-Echo响应 0 Echo响应报文 查询 3-目的不可达 0 目标网络不可达报文 差错 1 目标主机不可达报文 差错 2 目标协议不可达报文 差错 3 目标端口不可达报文 差错 4 要求分段并设置DF flag标志报文 差错 5 源路由…...
算法基础课第二部分
算法基础课 第四讲 数学知识AcWing1381. 阶乘(同余,因式分解) 质数AcWing 866. 质数的判定---试除法AcWing 868. 质数的判定---埃氏筛AcWing867. 分解质因数---试除法AcWing 197. 阶乘---分解质因数---埃式筛 约数AcWing 869. 求约数---试除法AcWing 870. 约数个数-…...

【数据结构】外部排序、多路平衡归并与败者树、置换-选择排序(生成初始归并段)、最佳归并树算法
目录 1、外部排序 1.1 基本概念 1.2 方法 2、多路平衡归并与败者树 2.1 K路平衡归并 2.2 败者树 3、置换-选择排序(生成初始归并段)编辑 4、最佳归并树 4.1 理论基础编辑 4.2 构造方法 编辑 5、各种排序算法的性质 1、外部排序 1.1 基本概…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
