在比特币上支持椭圆曲线 BLS12–381
通过使用智能合约实现来支持任何曲线
BLS12–381 是一种较新的配对友好型椭圆曲线。 与常用的 BN-256 曲线相比,BLS12-381 的安全性明显更高,并且安全目标是 128 位。

所有其他区块链,例如 Zcash 和以太坊,都必须通过硬分叉才能升级到新曲线,因为所使用的曲线是在协议级别进行硬编码的。 Zcash 花了一年多的时间在 Sapling 中升级。 以太坊 和 Tezos 在 2.5 多年前提出升级后仍未升级,如果他们打算升级的话。
比特币可以以智能合约的形式在本地运行 BLS12–381,无需任何重大更改。 下面的库为此提供了基础,使比特币成为目前唯一支持两条曲线的区块链,这要归功于其可编程性和可扩展性。 通过在智能合约中实施它们,可以类似地支持更多曲线,如 MNT4/6 和 BW。
以下内容最初由 Walker 发布在 Github 上,Walker 在首届比特币零知识证明黑客马拉松中获得第一名。
用于比特币零知识证明智能合约支持的 sCrypt BLS12–381 库。 目前的sCrypt零知识证明库是基于BN256,比特币的BLS12-381库是第一个在比特币上实现BLS12-381曲线配对验证的库。 现在您可以选择使用 BN256 或 BLS12–381 来实现零知识证明应用。 比特币是目前唯一支持零知识证明且可以选择多条曲线的区块链。
对于与平台无关的应用程序,选择需要在性能 (BN254) 和安全性 (BLS12–381) 之间进行权衡。 我们建议选择 BLS12–381,因为它更安全,速度也足够实用,但比 BN254 慢。
- BN254 (254bit, 32byte P):

- BLS12–381 (381bit, 48byte P):

参考:
- Groth16
- Efficient zk-SNARKs on Bitcoin: Technical Explainer
- BLS12–381 For The Rest Of Us
目录
- 曲线
- 曲折
- 高效配对
- 坐标系
- 蒙哥马利形式
- 先决条件
- 如何在本地运行
- 图书馆
- 应用程序接口
- 验证密钥和证明数据
- 测试
1. 曲线 BLS12–381
曲线 BLS12–381 既对配对友好(使其对数字签名有效)又对构建 zkSnarks 有效。 BLS12-381 的安全目标是 128 位。
1.1 曲线
BLS12–381 处理两条曲线,

配对是一个双线性映射,它以两个点作为输入,每个点来自一组相同阶数 r。 这两组称为 G1 和 G2 。
1.2 twist 扭曲
BLS12–381 使用扭曲,将扩展场的程度降低了六倍。 因此,扭曲曲线上的 G2 可以在 Fq2 而不是 Fq12 上定义,这大大节省了复杂性,在 Fq12 中进行算术运算非常复杂且效率低下。

这改变了原始曲线

进入曲线

所以这些是我们将使用的两个组:

1.3 高效配对
配对的计算有两个部分:
米勒循环:递归计算两个输入点 f(pointG1, pointG2) 的中间函数
最后求幂:将 f 提高到 c 的大幂
等式 1:

1.3.1 减少到 3 对
验证等式2:

其中 α 和 β 在设置时已知,因此我们可以预先计算第二对 e(α, β) 并用它替换 α 和 β 作为验证密钥的一部分,从而节省一对。
1.3.2 最终一次求幂
等式 2 可以重写为:

e是双线性的,把指数(-1)移到括号里。

代入等式 1,我们得到:

而不是计算 4 次计算密集型的最终指数,我们最后只需要做一次。
注意,snarkjs/circom 的 verification_key.json 输出文件中,有一个 vk_alphabeta_12 预计算项,但是你不能用它来预计算 f(α,β),这个数据是通过miller循环和finanl求幂 f( α, β)^c 。 您可以在调试模式下运行 testcase1.scrypt 合约以获取预先计算的 f(α, β) 数据。
1.4 坐标系
查找域元素的逆是一项昂贵的操作,因此椭圆曲线算法的实现会尽量避免它。
1.4.1 仿射坐标
仿射坐标是仅具有 (x, y) 坐标对的点的传统表示,其中 x 和 y 满足曲线方程。 这是我们通常在存储和传输点时使用的。
基本思想是使用名义分数来表示坐标,减少所需的实际除法运算次数。 为此,引入了第三个坐标并使用 (X, Y, Z) 作为点的内部表示。
1.4.2 雅可比(Jacobian)坐标
雅可比点 (X, Y, Z) 表示仿射点 (X/Z², Y/Z³)。 曲线方程变为:

请注意,导入仿射点 (x,y) 的最简单方法是将其映射到 (x, y, 1)。
1.5 蒙哥马利形式
一种不需要除法的模数计算方法是所谓的蒙哥马利乘法。 要计算模乘运算,
- 将乘数转换为蒙哥马利形式
- 使用蒙哥马利乘法
- 转换蒙哥马利形式的结果
2. 准备
- Visual Studio Code(VSC)
- sCrypt IDE
- Node.js,
version >= 12 - PC CPU >= 2.6GHz, Memory >= 24GB
3.如何在本地运行
运行 npm install 来安装依赖
从 VSCode GUI 运行测试用例,选择 testcase0.scrypttest.js 文件,在文件编辑窗口单击鼠标右键,选择菜单 Run sCrypt Test
4. 库和 API
4.1 库
├─ contracts
│ ├─ bls12381.scrypt # bls12-381 library
│ ├─ bls12381pairing.scrypt # bls12-381 ZKP lib(Optimized 3-pairs)
│ └─ zksnark12381.scrypt # zk-SNARKs verifier contract example
└─ tests└─ js├─ testcase0.scrypttest.js # simple testcase├─ testcaseAzksnark.scrypttest.js # testcase A├─ testcaseBzksnark.scrypttest.js # testcase B├─ testcaseCzksnark.scrypttest.js # testcase C└─ testcaseDzksnark.scrypttest.js # testcase D
4.2 API
static function pairCheck3Point(PointG1 a0, PointG2 b0,fe12 millerb1a1,PointG1 a2, PointG2 b2,PointG1 a3, PointG2 b3) : bool
参数 (3对 pairing and 1 对预先计算好的pairing):
- a0 : A, b0 : B
- millerb1a1 : 预先计算
miller(α, β) - a2 : L, b2 : ϒ
- a3 : C, b3 : δ

验证等式 2:

4.2.1 从 snarkjs/Circom 验证密钥和证明数据

您可以通过 scrypt.io 找到 zkSNARK snarkjs/Circom 教程
执行snarkjs/Circom命令时需要选择bls12381曲线命令行选项,因为默认是bn128曲线。 例如,
- 编译电路
circom ../work_circom/factor.circom --r1cs --wasm --prime bls12381
- 开始新的 powers of tau 仪式
snarkjs powersoftau 新 bls12-381 12 pot12_0000.ptau
然后可以确认输出的 verification_key.json 和 proof.json 文件中有一个"curve": “bls12381"项,而不是"curve”: "bn128"项。
从 proof.json 文件中获取A、B、C参数,从 verification_key.json 文件中获取 α、β、ϒ、δ参数,使用 public.json 文件中的ic item和公共输入计算 L 参数:

其中公共输入 w = (1, w1, …, wi)
4.2.2 verification_key.json
测试用例 B verification_key.json
{"protocol": "groth16","curve": "bls12381","nPublic": 1,"vk_alpha_1": ["32346008969010......", "760490433841......", "1"],"vk_beta_2": [["62735191543702......", "379194604638......"],["94606778762315......", "299061862927......"],["1", "0"]],"vk_gamma_2": [["3527010695874......", "305914434424......"],["1985150602287......", "927553665492......"],["1", "0"]],"vk_delta_2": [["1895592553603......", "338057034563......"],["1793381858589......", "319699776756......"],["1", "0"]],"vk_alphabeta_12": [[["29062082199832......", "29798557291243......"],["20107026956616......", "32289268603827......"],["37794026319284......", "20272682142916......"]],[["11743275386962......", "32259555688411......"],["30689582621397......", "26992620205415......"],["75601830939387......", "26615242825680......"]]],"IC": [["179858356000600......", "10944984983678......", "1"],["341669953409364......", "26956794051246......", "1"]]
}
4.2.3 proof.json
测试用例 A proof.json
{"pi_a": ["386406607244204......", "3355814159298......", "1"],"pi_b": [["28933956745182......", "3829761206156......"],["36211079726457......", "6620758983513......"],["1", "0"]],"pi_c": ["302947598381396......", "3994710045276......", "1"],"protocol": "groth16","curve": "bls12381"
}
4.2.4 public.json
测试用例 A public.json
["13221"
]
5. 测试用例
5.1 设计电路
用 Circom 语言实现一个电路。 例如,这个简单的证明人们知道将整数 n 分解为两个整数而不透露整数。 该电路有两个名为 p 和 q 的私有输入以及一个名为 n 的公共输入。
// p and q are factorizations of n
pragma circom 2.0.0;template Factor() {// Private Inputs:signal input p;signal input q;// Public Inputs:signal output n;assert(p > 1);assert(q > 1);n <== p * q;
}
component main = Factor();
5.2 测试用例 A, B, C, D
两个私有输入 p 和 q,以及一个公共输入 n。

5.3 测试网部署
合约:
zksnark12381deploy.scrypt
部署和解锁

测试网部署交易:
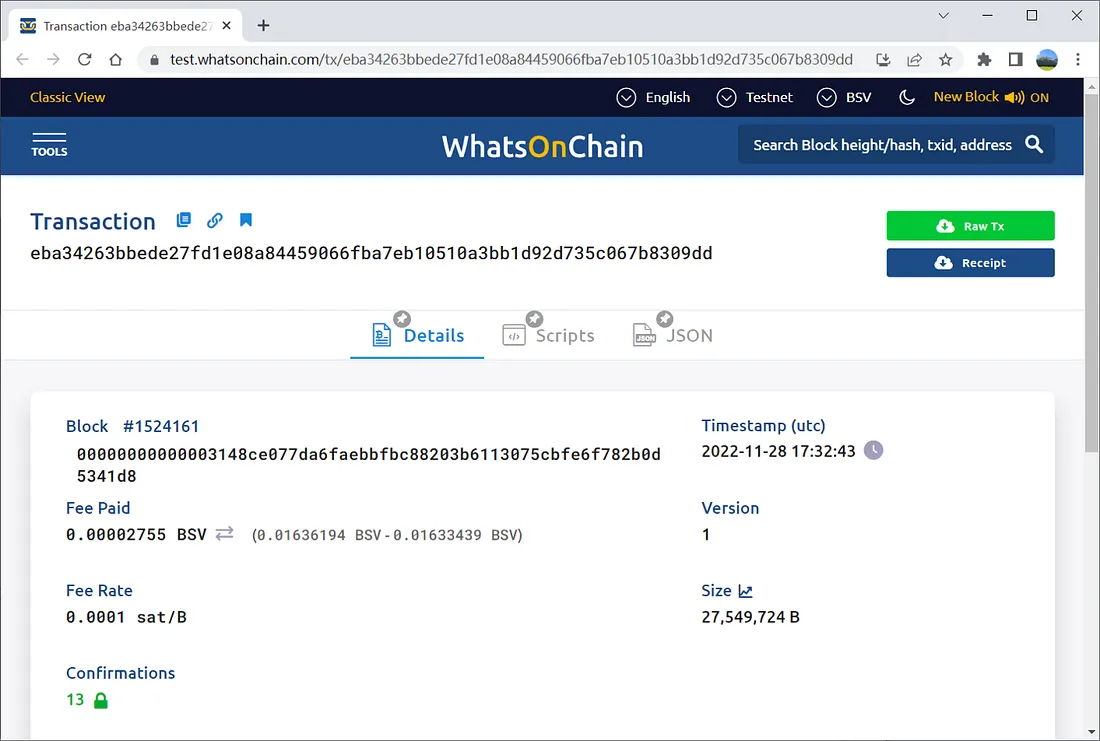
交易: eba34263bbede27fd1e08a84459066fba7eb10510a3bb1d92d735c067b8309dd
相关文章:

在比特币上支持椭圆曲线 BLS12–381
通过使用智能合约实现来支持任何曲线 BLS12–381 是一种较新的配对友好型椭圆曲线。 与常用的 BN-256 曲线相比,BLS12-381 的安全性明显更高,并且安全目标是 128 位。 所有其他区块链,例如 Zcash 和以太坊,都必须通过硬分叉才能升…...
简单讲解 glm::mat4
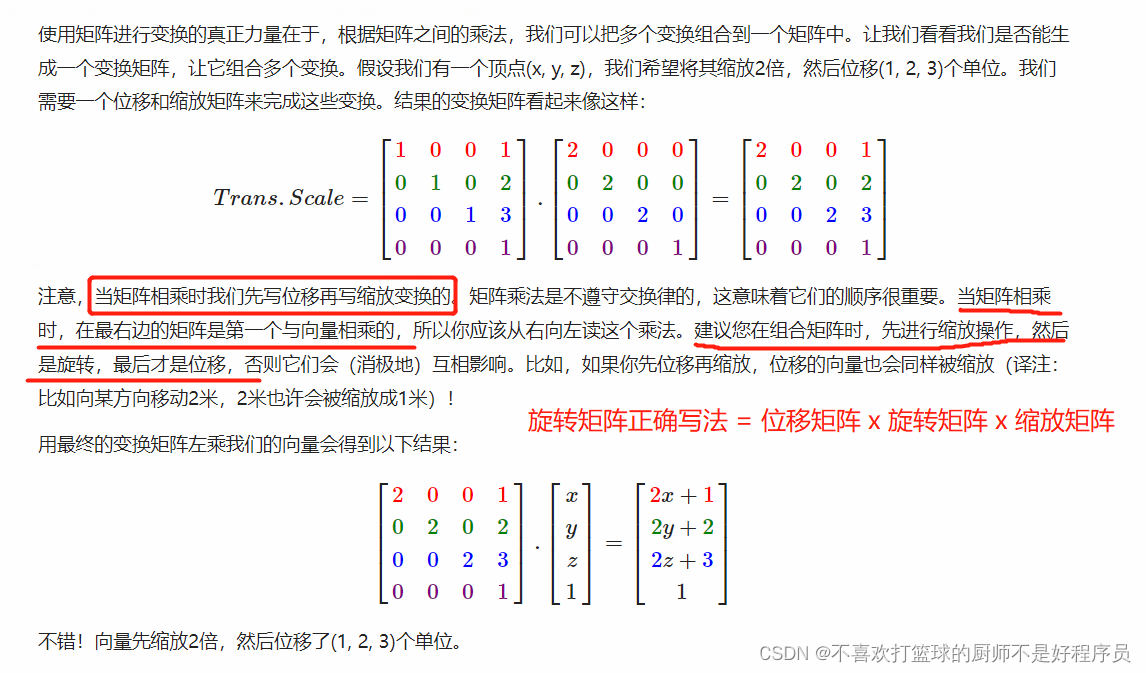
文章目录 前言一、下载glm库二、基本数学知识1. 三维中的 4 x 4 矩阵2.旋转3. 位移4. 缩放5. 组合 三、行向量或列向量四、总结 前言 glm库是OpenGL的官方数学库,里面内置多种跟几何变换相关的函数,熟练掌握glm库可以省下很多麻烦。 因为最近在项目中主…...

第3章-指标体系与数据可视化-3.1.1-Matplotlib绘图库
目录 3.1 Python可视化 3.1.1 Matplotlib绘图库 1. 线图 2. 饼图 3. 条形图 4. 直方图 5.散点图...

探索视听新纪元: ChatGPT的最新语音和图像功能全解析
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🤖 人工智能 AI: 🧠 Machine …...
华为乾坤区县教育安全云服务解决方案(1)
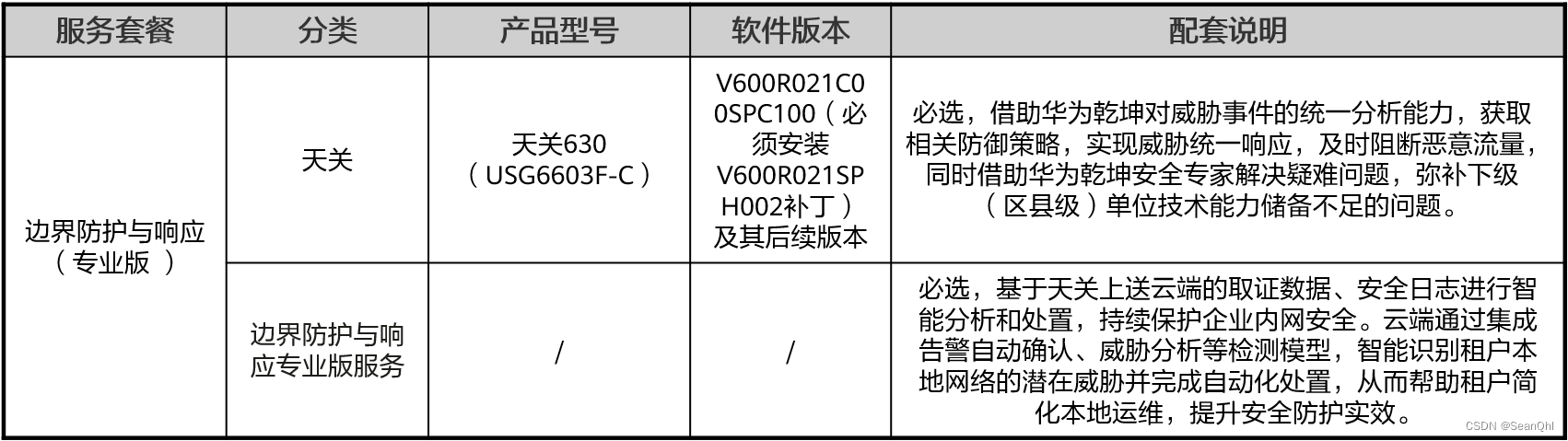
华为乾坤区县教育安全云服务解决方案(1) 课程地址方案背景客户痛点分析区县教育网概述区县教育网业务概述区县教育网业务安全风险分析区县教育网安全运维现状分析区县教育网安全建设痛点分析 安全解决方案功能概述架构概述方案架构设备选型 课程地址 本…...

《Jetpack Compose从入门到实战》第三章 定制 UI 视图
目录 配置颜色、字体与形状Welcome PageLogin PageHome Page 主题CompositionLocal 配置颜色、字体与形状 -ui.theme.Color.kt val pink100 Color(0xFFFFF1F1) val pink900 Color(0xFF3F2C2C) val white Color(0xFFFFFFFF) val white850 Color(0xD9FFFFFF) val gray Col…...
Kubernetes组件和架构简介
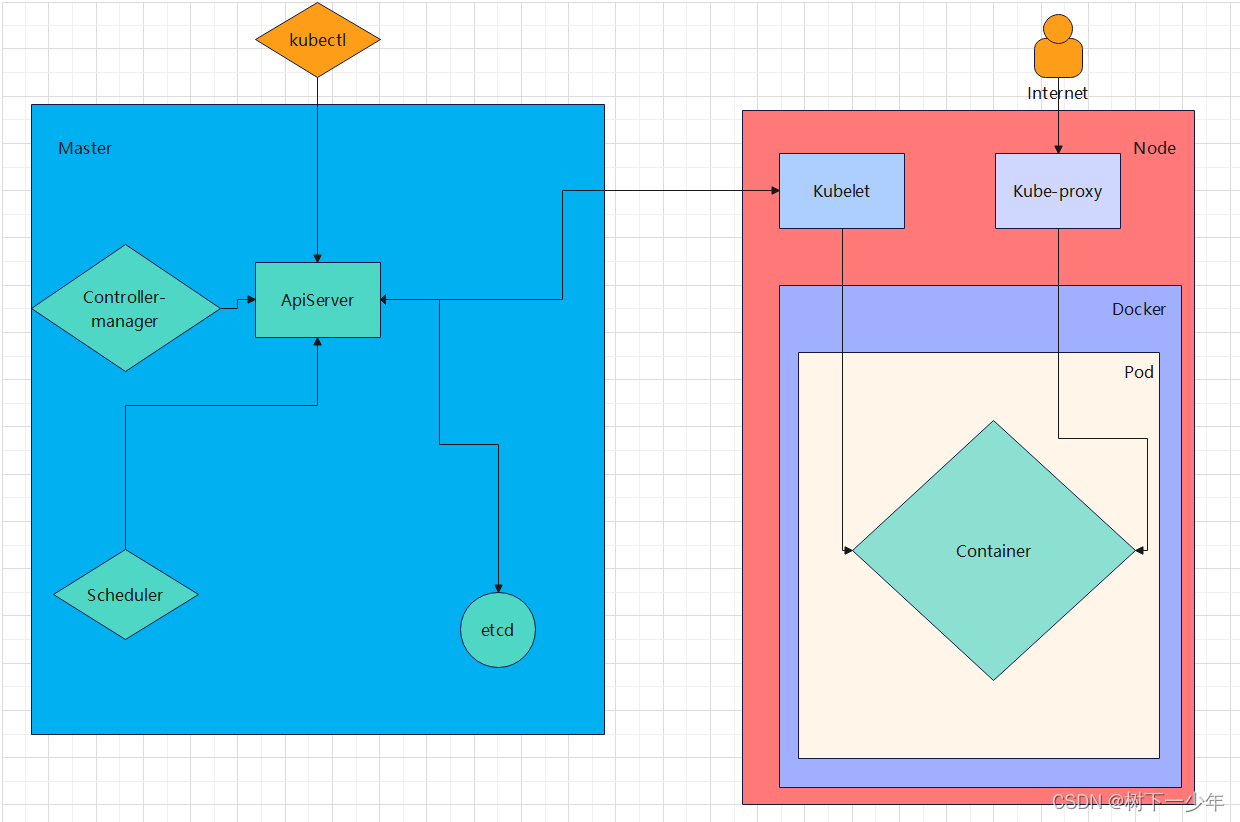
目录 一.概念简介 1.含义: 2.主要功能: 3.相关概念: 二.组件和架构介绍 1.master:集群的控制平面,管理集群 2.node:集群的数据平面,为容器提供工作环境 3.kubernetes简单架构图解 一.概…...
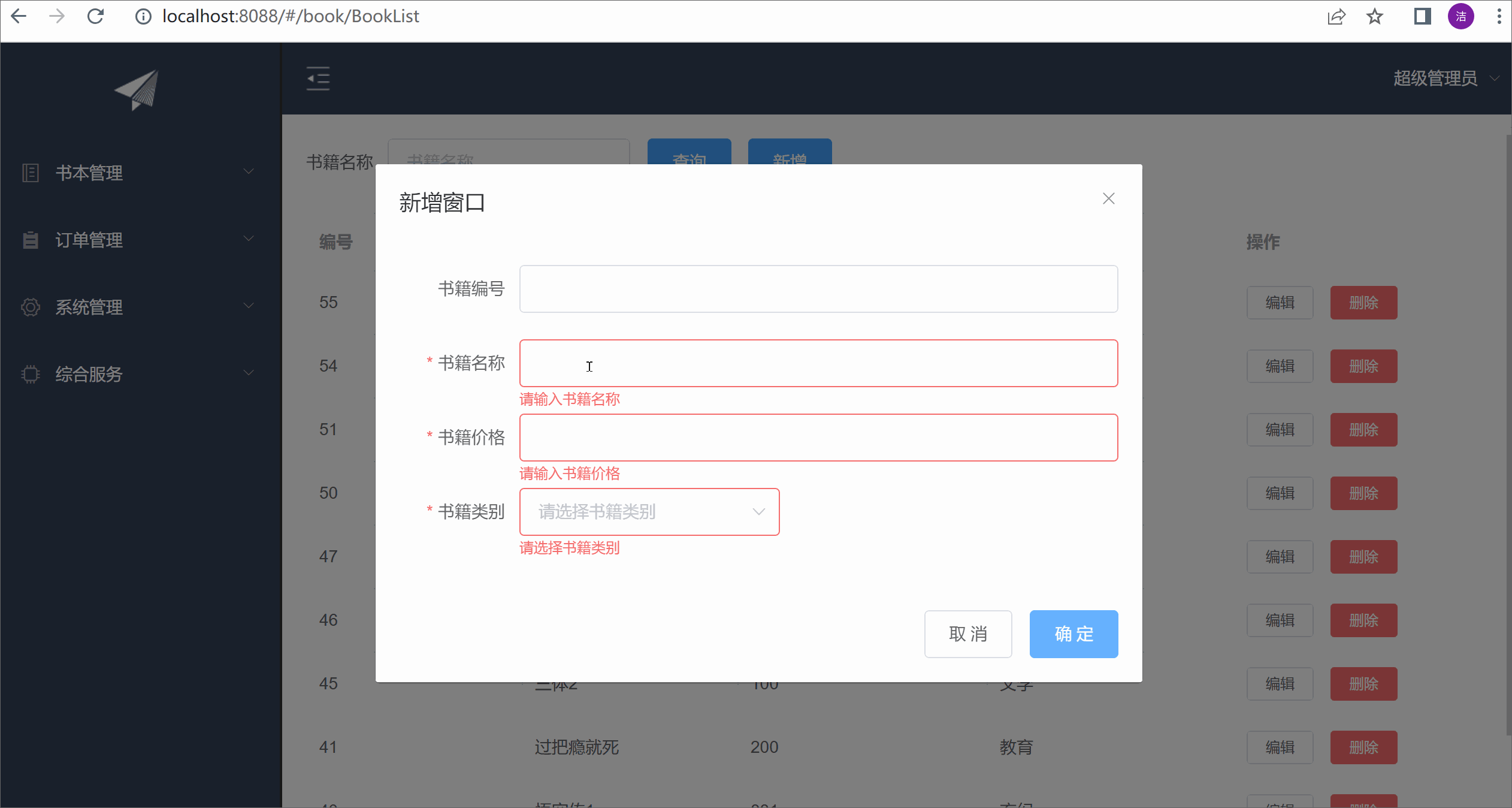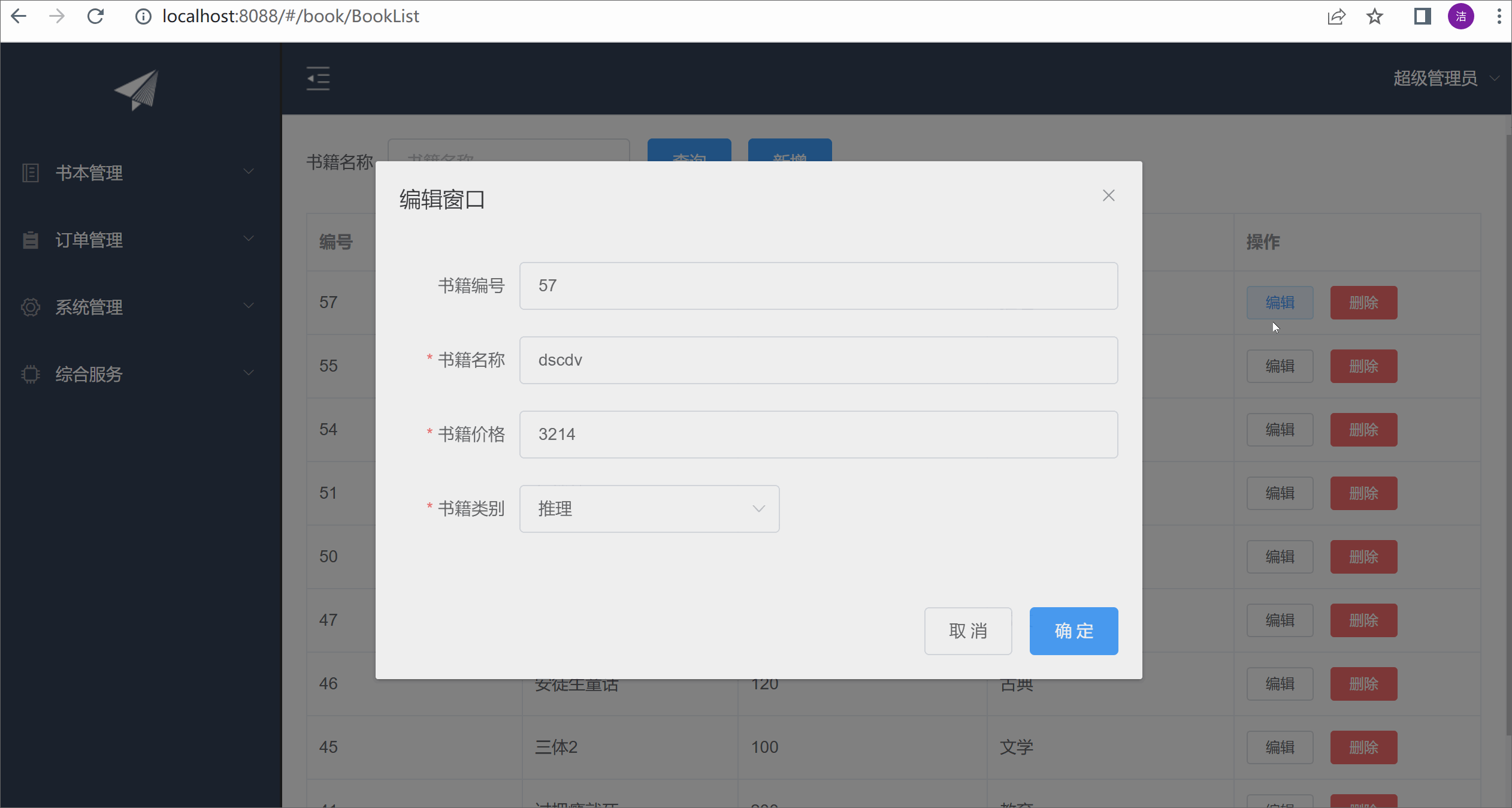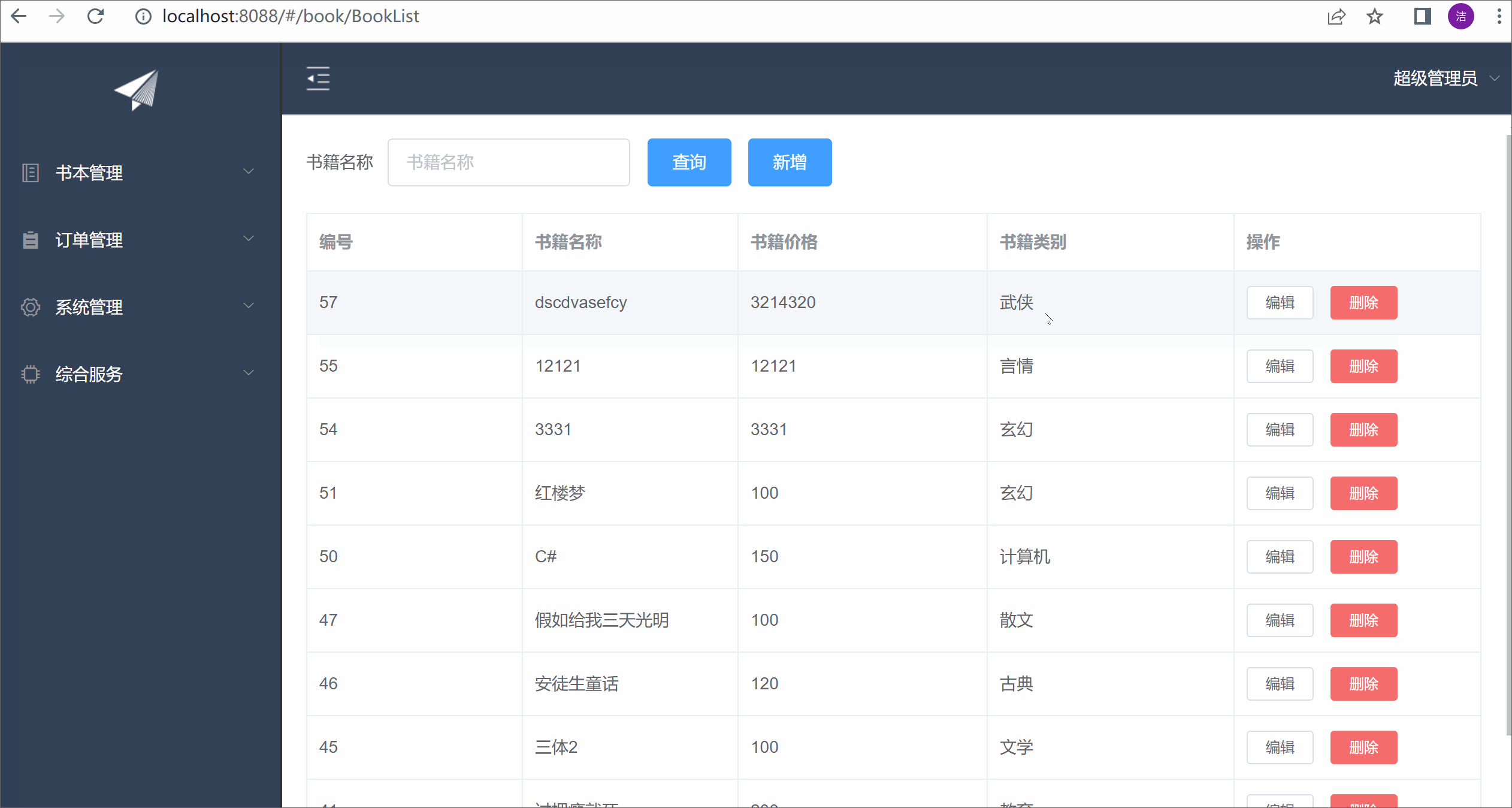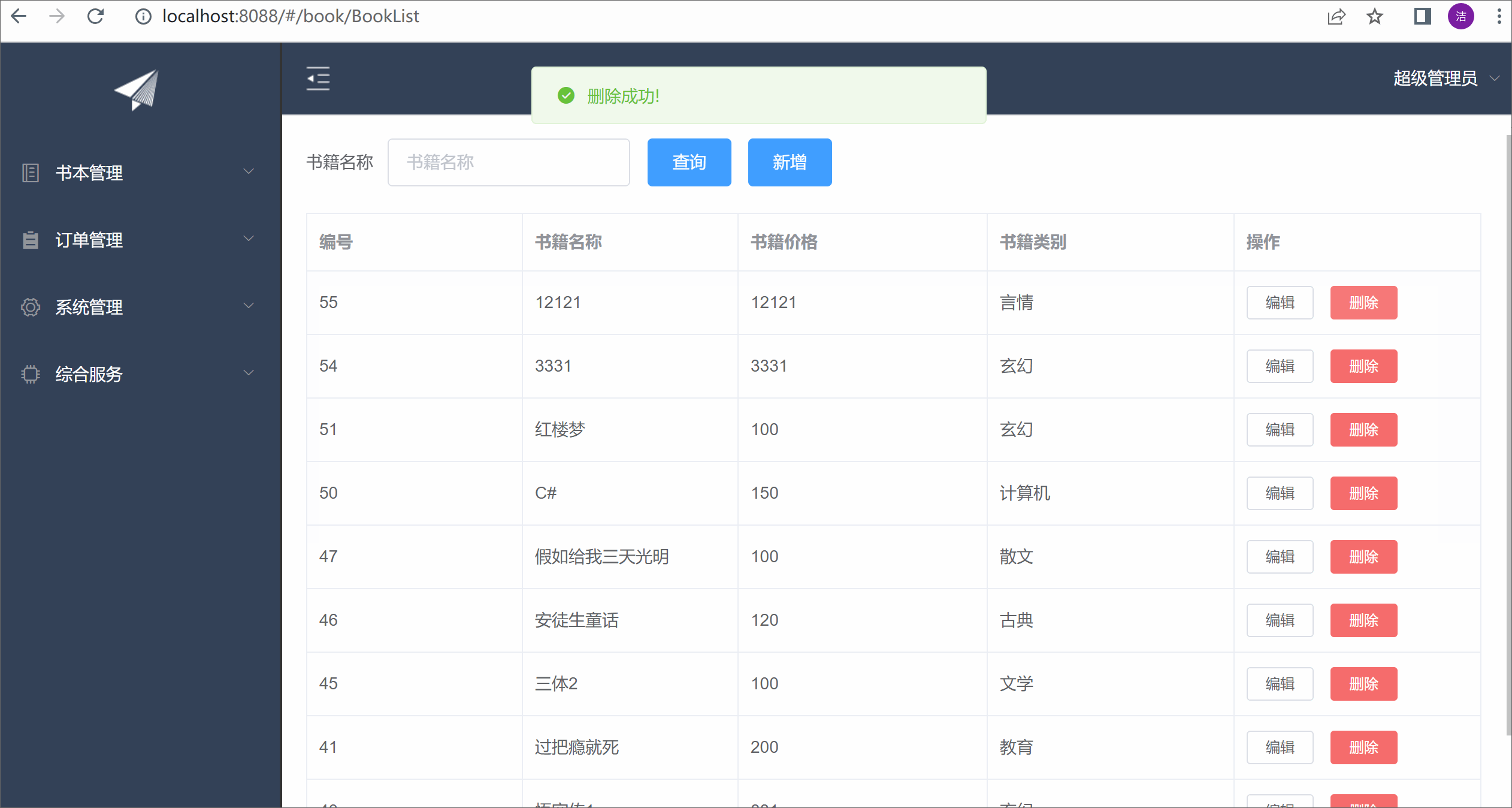
ElementUI实现增删改功能以及表单验证
目录 前言 BookList.vue action.js 展示效果 前言 本篇还是在之前的基础上,继续完善功能。上一篇完成了数据表格的查询,这一篇完善增删改,以及表单验证。 BookList.vue <template><div class"books" style"pa…...

C++中有哪些运算符以及它们的优先级?
C中常用的运算符包括算术运算符、赋值运算符、关系运算符、逻辑运算符、位运算符等。这里列举一些常见的运算符以及它们的优先级(从高到低): 圆括号()一元正号、一元负号-数组下标[]成员选择符(点号.、箭头…...

uboot启动流程-涉及_main汇编函数
一. uboot启动流程涉及函数 本文简单分析一下 save_boot_params_ret调用的函数:_main汇编函数。 本文继之前文章的学习,地址如下: uboot启动流程-涉及s_init汇编函数_凌肖战的博客-CSDN博客 二. uboot启动流程涉及的 _main汇编函数 经过之…...

此芯科技加入百度飞桨硬件生态共创计划,加速端侧AI生态布局
近日,此芯科技(上海)有限公司(以下简称“此芯科技”)与百度签署硬件生态共创计划合作协议,正式加入由百度发起的硬件生态共创计划。双方将共同推动端侧AI和大模型在个人计算、车载计算以及元宇宙计算等领域…...
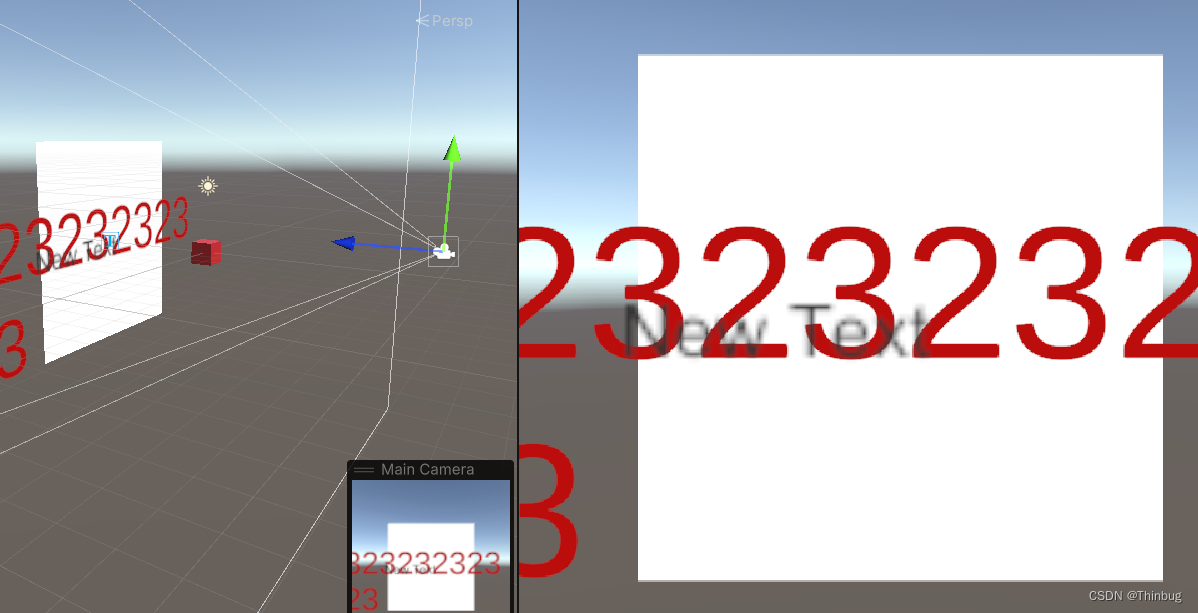
Unity把UGUI再World模式下显示到相机最前方
Unity把UGUI再World模式下显示到相机最前方 通过脚本修改Shader 再VR里有时候要把3D的UI显示到相机最前方,加个UI相机会坏事,可以通过修改unity_GUIZTestMode来解决。 测试用例 测试用例如下: 场景包含一个红色的盒子,一个UI…...
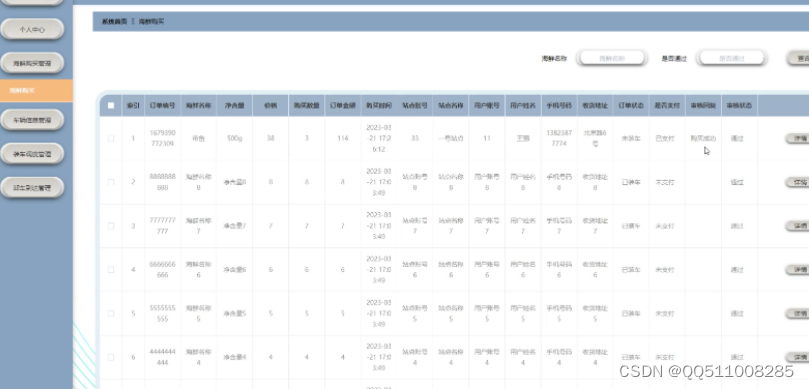
nodejs+vue活鲜物流监控系统elementui
第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:技术背景 5 3.2.2经济可行性 6 3.2.3操作可行性: 6 3.3 项目设计目标与原则 6 3.4系统流程分析 7 3.4.1操作流程 7 3.4.2添加信息流程 8 3.4.3删除信息流程 9 第4章 系统设计 11 …...
数据集划分——train_test_split函数使用说明
当我们拿到数据集时,首先需要对数据集进行划分训练集和测试集,sklearn提供了相应的函数供我们使用 一、讲解 快速随机划分数据集,可自定义比例进行划分训练集和测试集 二、官网API 官网API sklearn.model_selection.train_test_split(*a…...

Pytorch中关于forward函数的理解与用法
目录 前言1. 问题所示2. 原理分析2.1 forward函数理解2.2 forward函数用法 前言 深入深度学习框架的代码,发现forward函数没有被显示调用 但代码确重写了forward函数,于是好奇是不是python的魔术方法作用 1. 问题所示 代码如下所示: cla…...
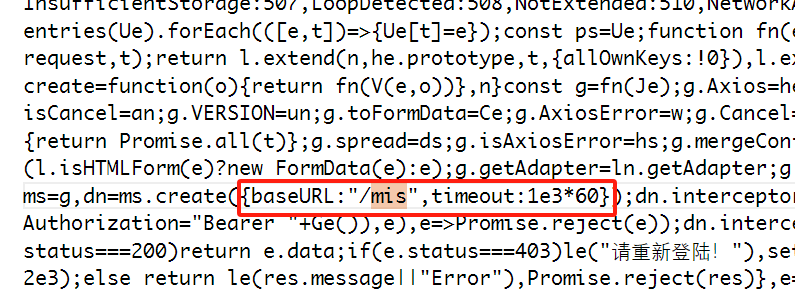
vite跨域proxy设置与开发、生产环境的接口配置,接口在生产环境下,还能使用proxy代理地址吗
文章目录 vite的proxy开发环境设置如果后端没有提供可以替换的/mis等可替换的后缀的处理办法接口如何区分.env.development开发和.env.production生产环境接口在生产环境下,还能使用proxy代理地址吗? vite的proxy开发环境设置 环境: vite 4…...
【嵌入式】使用MultiButton开源库驱动按键并控制多级界面切换
目录 一 背景说明 二 参考资料 三 MultiButton开源库移植 四 设计实现--驱动按键 五 设计实现--界面处理 一 背景说明 需要做一个通过不同按键控制多级界面切换以及界面动作的程序。 查阅相关资料,发现网上大多数的应用都比较繁琐,且对于多级界面的…...

【数据结构】树的概念理解和性质推导(保姆级详解,小白必看系列)
目录 一、前言 🍎 为什么要学习非线性结构 ---- 树(Tree) 💦 线性结构的优缺点 💦 优化方案 ----- 树(Tree) 💦 树的讲解流程 二、树的概念及结构 🍐 树的概念 &…...
融合之力:数字孪生、人工智能和数据分析的创新驱动
数字孪生、人工智能(AI)和数据分析是当今科技领域中的三个重要概念,它们之间存在着紧密的关联和互动,共同推动了许多领域的创新和发展。 一、概念 数字孪生是一种数字化的模拟技术,它通过复制现实世界中的物理实体、…...

Spring的注解开发-Spring配置类的开发
Bean配置类的注解开发 Component等注解替代了<bean>标签,但像<import>、<context:componentScan>等非<bean>标签怎样去使用注解去替代呢?定义一个配置类替代原有的xml配置文件,<bean>标签以外的标签ÿ…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
)
使用python进行图像处理—图像滤波(5)
图像滤波是图像处理中最基本和最重要的操作之一。它的目的是在空间域上修改图像的像素值,以达到平滑(去噪)、锐化、边缘检测等效果。滤波通常通过卷积操作实现。 5.1卷积(Convolution)原理 卷积是滤波的核心。它是一种数学运算,…...

Vue 实例的数据对象详解
Vue 实例的数据对象详解 在 Vue 中,数据对象是响应式系统的核心,也是组件状态的载体。理解数据对象的原理和使用方式是成为 Vue 专家的关键一步。我将从多个维度深入剖析 Vue 实例的数据对象。 一、数据对象的定义方式 1. Options API 中的定义 在 Options API 中,使用 …...
