数据结构第12周 :( 有向无环图的拓扑排序 + 拓扑排序和关键路径 + 确定比赛名次 + 割点 )
目录
- 有向无环图的拓扑排序
- 拓扑排序和关键路径
- 确定比赛名次
- 割点
有向无环图的拓扑排序
【问题描述】
由某个集合上的一个偏序得到该集合上的一个全序,这个操作被称为拓扑排序。偏序和全序的定义分别如下:若集合X上的关系R是自反的、反对称的和传递的,则称R是集合X上的偏序关系。设R是集合X上的偏序,如果对每个x,y∈X必有xRy或yRx,则称R是集合X上的全序关系。由偏序定义得到拓扑有序的操作便是拓扑排序。
拓扑排序的流程如下:
-
在有向图中选一个没有前驱的顶点并且输出之;
-
从图中删除该顶点和所有以它为尾的弧。
重复上述两步,直至全部顶点均已输出,或者当前图中不存在无前驱的顶点为止。后一种情况则说明有向图中存在环。
在本题中,读入一个有向图的邻接矩阵(即数组表示),建立有向图并按照以上描述中的算法判断此图是否有回路,如果没有回路则输出拓扑有序的顶点序列。
【输入形式】
输入的第一行包含一个正整数n,表示图中共有n个顶点。其中n不超过50。
以后的n行中每行有n个用空格隔开的整数0或1,对于第i行的第j个整数,如果为1,则表示第i个顶点有指向第j个顶点的有向边,0表示没有i指向j的有向边。当i和j相等的时候,保证对应的整数为0。
【输出形式】
如果读入的有向图含有回路,请输出“ERROR”,不包括引号。
如果读入的有向图不含有回路,请按照题目描述中的算法依次输出图的拓扑有序序列,每个整数后输出一个空格。
请注意行尾输出换行。
【样例输入】
4
0 1 0 0
0 0 1 0
0 0 0 0
0 0 1 0
【样例输出】
3 0 1 2
【说明】请注意采用邻接表存储结构时,链表创建需采用尾插法,以保证后续结点从小到大排列。
在本题中,需要严格的按照题目描述中的算法进行拓扑排序,并在排序的过程中将顶点依次储存下来,直到最终能够判定有向图中不包含回路之后,才能够进行输出。
另外,为了避免重复检测入度为零的顶点,可以通过一个栈结构维护当前处理过程中入度为零的顶点。
#include<iostream>
#include<stdlib.h>
#include<stack>
#define N 50
using namespace std;typedef struct node
{int data;struct node * next;
}ArcNode;typedef struct
{int in; //表示该节点的入度int vertex; // 该节点的信息int flag; //判断该节点是否入栈的标志ArcNode * firstedge;
}ALGraph;ALGraph G[N];
int res[N];void TopoSort(int limit)
{stack<ALGraph*> s;int count = 0;int i = 0;for(i = 0; i < limit; i ++){if(G[i].in == 0){s.push(&G[i]);G[i].flag = 0;}}while(!s.empty()){ALGraph * pos = s.top();s.pop();count ++;res[count] = pos->vertex;ArcNode * p = pos->firstedge;while(p != NULL){int num = p->data;G[num].in --;p = p->next;}for(i = 0 ; i <limit; i ++){if(G[i].in == 0 && G[i].flag == 1){s.push(&G[i]);G[i].flag = 0;}}}if(count == limit){for(i = 1; i <= limit; i ++){cout<<res[i]<<" ";}}else{cout<<"ERROR";}
}int main()
{int NodeNum = 0;cin>>NodeNum;int i = 0;int j = 0;for(i = 0; i < NodeNum; i ++) //邻接表初始化{G[i].in = 0;G[i].vertex = i;G[i].flag = 1;G[i].firstedge = NULL;}for(i = 0; i < NodeNum; i ++){for(j = 0; j < NodeNum; j ++){int num;cin>>num;if(num == 0) continue;else{ArcNode * temp = (ArcNode*)malloc(sizeof(ArcNode));temp->data = j;temp->next = NULL;ArcNode * pos = G[i].firstedge;while(1){if(pos == NULL) break;if(pos->next == NULL) break;elsepos = pos->next;}if(pos == NULL){G[i].firstedge = temp;}else{pos->next = temp;}G[j].in ++;}}}TopoSort(NodeNum);return 0;
}
拓扑排序和关键路径
【问题描述】若在带权的有向图中,以顶点表示事件,以有向边表示活动,边上的权值表示活动的开销(如该活动持续的时间),则此带权的有向图称为AOE网。如果用AOE网来表示一项工程,那么,仅仅考虑各个子工程之间的优先关系还不够,更多的是关心整个工程完成的最短时间是多少;哪些活动的延期将会影响整个工程的进度,而加速这些活动是否会提高整个工程的效率。因此,通常在AOE网中列出完成预定工程计划所需要进行的活动,每个活动计划完成的时间,要发生哪些事件以及这些事件与活动之间的关系,从而可以确定该项工程是否可行,估算工程完成的时间以及确定哪些活动是影响工程进度的关键。
【输入形式】第一行输入两个数字,分别表示顶点数和边数;从第二行开始,输入边的信息,格式为(i,j, weight)
【输出形式】关键路径的总时间(最大路径长度),代表关键活动的边,格式为(顶点1,顶点2),按大小顺序排列
【样例输入】
6 8
0 1 3
0 2 2
1 3 2
1 4 3
2 3 4
2 5 3
3 5 2
4 5 1
【样例输出】
8
0 2
2 3
3 5
#include<iostream>
#define N 50
#include<stack>
#include<stdlib.h>
using namespace std;typedef struct node
{int NodeId;int weight;int edgeId;struct node * next;
}ArcNode; //邻接结点结构体typedef struct
{int in;int out;int flag;int vertex;ArcNode * firstedge;
}ALGraph; //邻接表结构体ALGraph G[N];
int Relation[N][N];
int VE[N];
int VL[N];
int EE[N];
typedef struct
{int Weight;int node1;int node2;
}point;
point EL[N];
int el[N];
int count = -1;void MaxPathLen(int limit)
{int i = 0;stack<ALGraph*> S;//用入度来处理正向拓扑排序(填充VEfor(i = 0; i < limit; i ++){if(G[i].in == 0){S.push(&G[i]);G[i].flag = 0;}}while(!S.empty()){ALGraph * temp = S.top();S.pop();ArcNode * p = temp->firstedge;while(p != NULL) //弹出的节点的相邻节点的入度减一,填充VE{G[p->NodeId].in --;if(VE[temp->vertex] + p->weight > VE[p->NodeId]){VE[p->NodeId] = VE[temp->vertex] + p->weight;//cout<<p->NodeId<<" "<<VE[p->NodeId]<<endl;}p = p->next;}for(i = 0; i < limit; i ++){if(G[i].in == 0 && G[i].flag == 1){S.push(&G[i]);G[i].flag = 0;}}}for(i = 0; i < limit; i ++){G[i].flag = 1; //将标记初始化}int max = -1;int maxid = 0;for(i = 0; i < limit; i ++){if(VE[i] > max){max = VE[i];maxid = i;}}VL[maxid] = max;//用出度来处理逆向拓扑排序(填充VLfor(i = 0; i < limit; i ++){if(G[i].out == 0){S.push(&G[i]);G[i].flag = 0;}}while(!S.empty()){ALGraph * temp = S.top();S.pop();for(i = 0; i < limit; i ++){if(Relation[temp->vertex][i] == 1){G[i].out --;Relation[temp->vertex][i] = 0;ArcNode * pos = G[i].firstedge;while(pos->NodeId != temp->vertex) pos = pos->next;if(VL[i] == 0){VL[i] = VL[temp->vertex] - pos->weight;}if(VL[temp->vertex] - pos->weight < VL[i] ){VL[i] = VL[temp->vertex] - pos->weight;//cout<<temp->vertex<<" "<<VL[temp->vertex]<<" "<<pos->weight<<endl;}}}for(i = 0; i < limit; i ++){if(G[i].out == 0 && G[i].flag == 1){S.push(&G[i]);G[i].flag = 0;}}}//计算EE[N],EL[N]for(i = 0; i <= count; i ++){int e = EE[i];int l = EL[i].node2;EE[i] = VE[e];el[i] = VL[l] - EL[i].Weight;}cout<<max<<endl;for(i = 0; i <= count; i ++){if(EE[i] == el[i])cout<<EL[i].node1<<" "<<EL[i].node2<<endl;}
}int main()
{int NodeNum;int EdgeNum;cin>>NodeNum>>EdgeNum;int i, j;for(i = 0; i < NodeNum; i ++){VE[i] = 0;VL[i] = 0;}for(i = 0; i < EdgeNum; i ++){EE[i] = 0;el[i] = 0;EL[i].Weight = 0;EL[i].node1 = 0;EL[i].node2 = 0;}for(i = 0; i < NodeNum; i ++) //表的初始化{G[i].in = 0;G[i].out = 0;G[i].flag = 1;G[i].vertex = i;G[i].firstedge = NULL;}for(i = 0; i < NodeNum; i ++){for(j = 0; j < NodeNum; j ++){Relation[i][j] = 0;}}i = EdgeNum;while(i --) //表的填充{int node1;int node2;int w;cin>>node1>>node2>>w;Relation[node2][node1] = 1;ArcNode * temp = (ArcNode *)malloc(sizeof(ArcNode));temp->NodeId = node2;temp->weight = w;temp->next = NULL;count ++;EE[count] = node1;EL[count].node1 = node1;EL[count].node2 = node2;EL[count].Weight = w;temp->edgeId = count;G[node1].out ++;G[node2].in ++;ArcNode * pos = G[node1].firstedge;if(pos == NULL){G[node1].firstedge = temp;}else{while(1){if(pos->next == NULL) break;elsepos = pos->next;}pos->next = temp;}}MaxPathLen(NodeNum);return 0;
}
确定比赛名次
【问题描述】
此题为ACM竞赛真题,更强大的测试数据请自行前往以下链接进行代码提交验证。Problem - 1285 (hdu.edu.cn)
有N个比赛队(1<=N<=500),编号依次为1,2,3,。。。。,N进行比赛,比赛结束后,裁判委员会要将所有参赛队伍从前往后依次排名,但现在裁判委员会不能直接获得每个队的比赛成绩,只知道每场比赛的结果,即P1赢P2,用P1,P2表示,排名时P1在P2之前。现在请你编程序确定排名。
【输入形式】
输入有若干组,每组中的第一行为二个数N(1<=N<=500),M;其中N表示队伍的个数,M表示接着有M行的输入数据。接下来的M行数据中,每行也有两个整数P1,P2表示即P1队赢了P2队。
【输出形式】
给出一个符合要求的排名。输出时队伍号之间有空格,最后一名后面没有空格。
【样例输入】
4 3
1 2
2 3
4 3
【样例输出】
1 2 4 3
【样例说明】
符合条件的排名可能不是唯一的,此时要求输出时编号小的队伍在前;输入数据保证是正确的,即输入数据确保一定能有一个符合要求的排名。
#include<iostream>
#define N 50
#include<stdlib.h>
#include<stack>
using namespace std;typedef struct node
{int nodeId;struct node * next;
}ArcNode;typedef struct
{int in;int flag;int advtex;ArcNode * firstedge;
}ALGraph;ALGraph G[N];int main()
{int NodeNum;int EdgeNum;cin>>NodeNum>>EdgeNum;int i = 0;for(i = 1; i <= NodeNum; i ++){G[i].advtex = i;G[i].in = 0;G[i].flag = 1;G[i].firstedge = NULL;}i = EdgeNum;while(i --){int node1;int node2;cin>>node1>>node2;G[node1].advtex = node1;G[node2].in ++;ArcNode * pos = G[node1].firstedge;ArcNode * temp = (ArcNode*)malloc(sizeof(ArcNode));temp->nodeId = node2;temp->next = NULL;if(pos == NULL)G[node1].firstedge = temp;else{while(1){if(pos->next == NULL)break;elsepos = pos->next;}pos->next = temp;}}stack<ALGraph*> S;for(i = 1; i <= NodeNum; i ++){if(G[i].in == 0){S.push(&G[i]);G[i].flag = 0;break;}}while(!S.empty()){ALGraph * p = S.top();S.pop();cout<<p->advtex<<" ";ArcNode * pos = p->firstedge;while(pos != NULL){G[pos->nodeId].in --;pos = pos->next;}for(i = 1; i <= NodeNum; i ++){if(G[i].in == 0 && G[i].flag == 1){S.push(&G[i]);G[i].flag = 0;break;}}}return 0;
}
割点
【问题描述】
求一个无向连通图的割点。割点的定义是:若删除此结点和与其相关联的边,无向图不再连通。
ACM竞赛中有一些涉及到连通分量、割点、割边、缩点等知识点相关的题目,做完此题大家可自行前往以下链接查看并思考类似的题目,自行提交代码验证。Problem - 4587 (hdu.edu.cn)
【输入形式】
第一行是顶点个数及边的条数,后续每一行是每条边的两端关联的两个顶点
【输出形式】
割点,若没有割点,则输出NO
【样例输入】
7 8
A B
A D
B C
C D
C G
D E
D F
E F
【样例输出】
C D
【样例输入】
5 7
A B
B C
B D
A D
C D
A E
E C
【样例输出】
NO
#include<iostream>
#define N 50
using namespace std;int R[N][N];
int Dfn[N];
int Low[N];
int root = 0;
bool res[N];
int timestamp = 0;
int NodeNum; //节点个数
int RelationNum; //边的条数void Tarjan(int p)
{Dfn[p] = Low[p] = ++ timestamp;int i = 0;int cnt = 0;for(i = 0; i < NodeNum; i ++){if(R[p][i] == 1){if(Dfn[i] == 0){Tarjan(i);Low[p] = min(Low[p], Low[i]);if(Dfn[p] <= Low[i]){cnt ++;if(p != root || cnt >= 2){res[p] = 1;}}}elseLow[p] = min(Low[p], Dfn[i]);}}
}int main()
{cin>>NodeNum>>RelationNum;int i, j;for(i = 0; i < NodeNum; i ++){for(j = 0; j < NodeNum; j ++){R[i][j] = 0;}}i = RelationNum;while(i --){char node1;char node2;cin>>node1>>node2;int n1 = int(node1) - 65;int n2 = int(node2) - 65;R[n1][n2] = R[n2][n1] = 1;}for(root = 0; root < NodeNum; root ++){if(Dfn[root] == 0) Tarjan(root);}bool IsGe = false;for(i = 0; i < NodeNum; i ++){if(res[i]){ cout<<char(i + 'A')<<" ";IsGe = true;}}if(IsGe == false) cout<<"NO";return 0;
}
相关文章:
)
数据结构第12周 :( 有向无环图的拓扑排序 + 拓扑排序和关键路径 + 确定比赛名次 + 割点 )
目录有向无环图的拓扑排序拓扑排序和关键路径确定比赛名次割点有向无环图的拓扑排序 【问题描述】 由某个集合上的一个偏序得到该集合上的一个全序,这个操作被称为拓扑排序。偏序和全序的定义分别如下:若集合X上的关系R是自反的、反对称的和传递的&…...
)
Linux安装docker(无网)
1. 下载Docker安装包 下载地址:https://download.docker.com/linux/static/stable/x86_64/ 如果服务器可以联网可以通过wget下载安装包 wget https://download.docker.com/linux/static/stable/x86_64/docker-18.06.3-ce.tgz2. 解压安装 tar -zxvf docker-18.06…...

解决JNI操作内核节点出现写操作失败的问题
Android 9.0下,因为采取了SEAndroid/SElinux的安全机制,即使拥有root权限,或者对某内核节点设置为777的权限,仍然无法在JNI层访问。 本文将以用户自定义的内核节点/dev/wf_bt为例,手把手教会读者如何在JNI层获得对该节…...

纵然是在产业互联网的时代业已来临的大背景下,人们对于它的认识依然是短浅的
纵然是在产业互联网的时代业已来临的大背景下,人们对于它的认识依然是短浅的。这样一种认识的最为直接的结果,便是我们看到了各式各样的产业互联网平台的出现。如果一定要找到这些互联网平台的特点的话,以产业端为出发点,无疑是它…...

干翻 nio ,王炸 io_uring 来了 !!(图解+史上最全)
大趋势:全链路异步化,性能提升10倍 随着业务的发展,微服务应用的流量越来越大,使用到的资源也越来越多。 在微服务架构下,大量的应用都是 SpringCloud 分布式架构,这种架构总体上是全链路同步模式。 全链…...
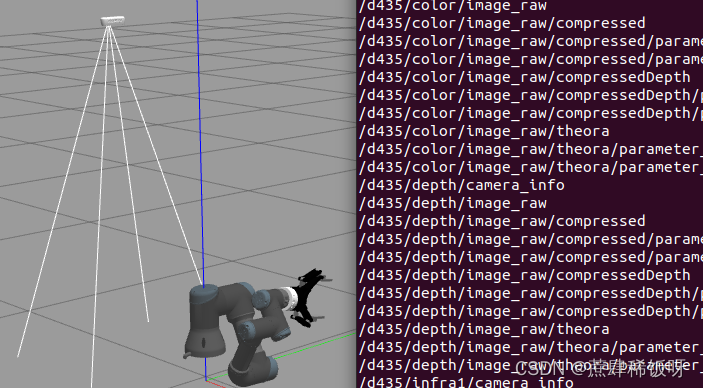
ur3+robotiq ft sensor+robotiq 2f 140+realsense d435i配置rviz,gazebo仿真环境
ur3robotiq ft sensorrobotiq 2f 140realsense d435i配置rviz,gazebo仿真环境 搭建环境: ubuntu: 20.04 ros: Nonetic sensor: robotiq_ft300 gripper: robotiq_2f_140_gripper UR: UR3 reasense: D435i 通过下面几篇博客配置好了ur3、力传…...

ASP.NET Core MVC 项目 AOP之Authorization
目录 一:说明 二:传统鉴权授权的基本配置 三 :角色配置说明 四:策略鉴权授权 五:策略鉴权授权Requirement扩展 总结 一:说明 鉴权:是指验证你是否登录,你登录后的身份是什么。…...
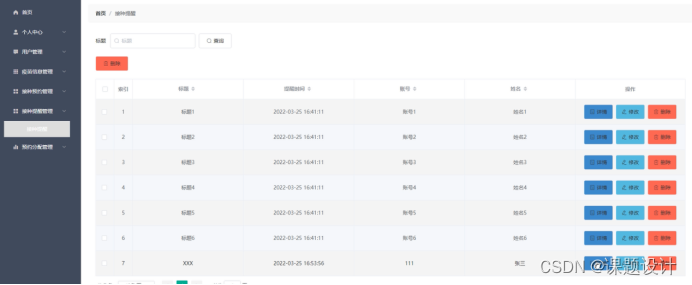
智能新冠疫苗接种助手管理系统
项目背景介绍 近几年来,网络事业,特别是Internet发展速度之快是任何人都始料不及的。目前,由于Internet表现出来的便捷,快速等诸多优势,已经使它成为社会各行各业,甚至是平民大众工作,生活不可缺少的一个重…...

Python+Selenium4元素交互1_web自动化(5)
目录 0. 上节回顾 1. 内置的等待条件 2. 元素属性 1. Python对象属性 2. HTML元素属性 3. 元素的交互 1. 输入框 2. 按钮 3. 单选框和复选框 0. 上节回顾 DEBUG的方式:JS断点 Python断点编程语言提供的等待方式:sleepselenium提供的等待方式&…...

2023双非计算机硕士应战秋招算法岗之深度学习基础知识
word版资料自取链接: 链接:https://pan.baidu.com/s/1H5ZMcUq-V7fxFxb5ObiktQ 提取码:kadm 卷积层 全连接神经网络需要非常多的计算资源才能支撑它来做反向传播和前向传播,所以说全连接神经网络可以存储非常多的参数,…...

Python opencv进行矩形识别
Python opencv进行矩形识别 图像识别中,圆形和矩形识别是最常用的两种,上一篇讲解了圆形识别,本例讲解矩形识别,最后的结果是可以识别出圆心,4个顶点,如下图: 左边是原始图像,右边是识别结果,在我i5 10400的CPU上,执行时间不到8ms。 识别出结果后,计算任意3个顶点…...

网安入门必备的12个kali Linux工具
kali Linux工具帮你评估 Web 服务器的安全性,并帮助你执行黑客渗透测试。 注意:这里不是所提及的所有工具都是开源的。 1. Nmap Nmap ( 网络映射器 )是一款用于 网络发现 和 安全审计 的 网络安全 工具. 主机发现,端口扫描,版本…...
【测试面试】头条大厂,测试开发岗真实一面。你能抵得住吗?
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 小吴: 现…...
分享app的测试技巧
前言 今天笔者想和大家来唠唠app测试,现在的app有非常的多,这些app都是需要经过测试之后才能发布到应用市场中,app已经成为了我们日常生活中不可或缺的一部分了,但它的功能必须强大,才能受到消费者的重视,…...

HTML 基础【快速掌握知识点】
目录 一、什么是HTML? 二、HTML的发展史 三、HTML5的优势 四、HTML基本结构 五、DOCTYPE声明 六、title标签 七、meta标签 八、标题标签 九、段落标签 十、换行标签 十一、水平线标签 十二、字体样式标签 十三、特殊符号 十四、图像标签 十五、链接标…...
SpringBoot入门(二)
这里写目录标题一、SpringBoot整合Junit1.1 搭建SpringBoot工程1.2 引入starter-test起步依赖1.3 编写类1.4 测试二、SpringBoot整合mybatis2.1 搭建SpringBoot工程2.2 引入mybatis起步依赖,添加驱动2.3 编写DataSource和MyBatis相关配置2.4 定义表和实体类2.5 编写…...
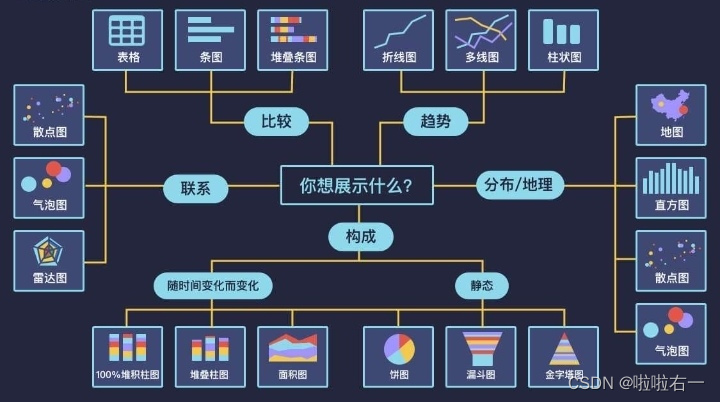
大数据|大数据基础(概念向)
目录 📚大数据概念 🐇常见数据存储单位 🐇大数据的特点(5V) 🐇大数据 VS 数据库 🌟数据库 🌟大数据 📚大数据业务分析基本步骤 🐇收集数据 Ǵ…...

若依配置教程(九)若依前后端分离版部署到服务器Nginx(Windows版)
搭建若依环境 要部署到服务器上,首先要在本地运行若依系统 文章目录搭建若依环境后端部署1.在application.yml中修改后台端口,这里默认是8080。2.在application-druid.yml中修改正式环境数据库。3.后端打包部署前端部署下载安装NginxNginx代理配置启动N…...
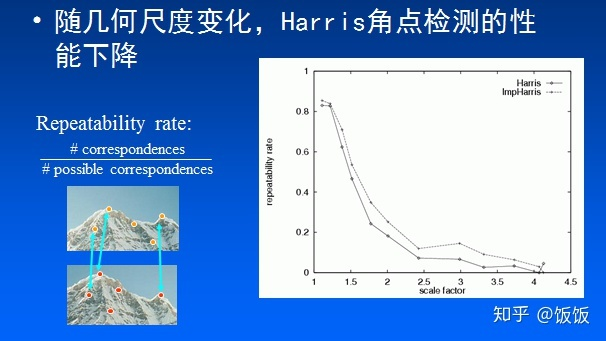
【仔细理解】计算机视觉基础1——特征提取之Harris角点
Harris角点是图像特征提取中最基本的方法,本篇内容将详细分析Harris角点的定义、计算方法、特点。 一、Harris角点定义 在图像中,若以正方形的小像素窗口为基本单位,按照上图可以将它们划分三种类型如下: 平坦区域:在任…...
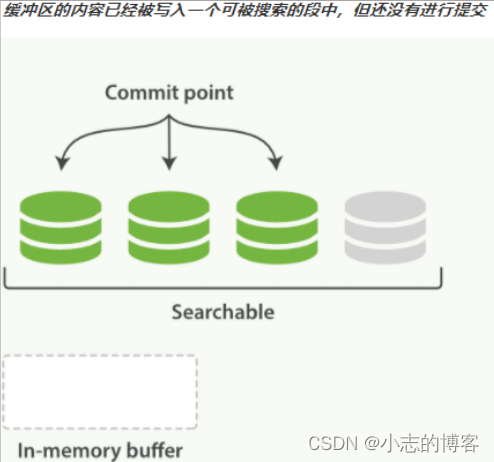
Elasticsearch7.8.0版本进阶——近实时搜索
目录一、近实时搜索的概述1.1、按段(per-segment)搜索1.2、更轻量的方式搜索二、为什么Elasticsearch是 近 实时搜索三、如何解决索引了一个文档然后却没有搜到四、哪种情况不需要每秒刷新4.1、使用 Elasticsearch 索引大量的日志文件4.2、使用 Elastics…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
