EM@坐标@函数@图象的对称和翻折变换
文章目录
abstract
- 坐标@函数@图象的对称和翻折变换
翻折变换
关于坐标轴翻折
- 此处我们通过研究图象上的点来间接图象变换,设图象的方程为 y = f ( x ) y=f(x) y=f(x), f ( x ) f(x) f(x)的定义域为 D f D_f Df
f ( − x ) , f ( x ) f(-x),f(x) f(−x),f(x)
- 函数 f ( − x ) f(-x) f(−x)可以看作是函数 u = − x u=-x u=−x和 y = f ( u ) y=f(u) y=f(u)复合而成的函数
- x ∈ D u = R x\in{D_u}=\mathbb{R} x∈Du=R
- 设函数 f ( x ) f(x) f(x)的定义域为 D f {D_f} Df,对于 g ( x ) = f ( − x ) g(x)=f(-x) g(x)=f(−x), − x ∈ D f -x\in{D_f} −x∈Df,即 x ∈ − D f x\in{-D_f} x∈−Df或作 D g = − D f D_g=-D_f Dg=−Df(表示 f , g f,g f,g的定义域关于原点对称)
- 若 a ∈ D f a\in{D_f} a∈Df,在 x = a x=a x=a处,可以取函数 f ( x ) f(x) f(x)上的点 A ( a , f ( a ) ) A(a,f(a)) A(a,f(a));
- − a ∈ D g -a\in{D_g} −a∈Dg, g ( x ) g(x) g(x)上一定存在点 B ( − a , f ( a ) ) B(-a,f(a)) B(−a,f(a));
- 显然 A , B A,B A,B关于 y y y轴对称,对定义域内所有 x x x对应的点 ( x , f ( x ) ) (x,f(x)) (x,f(x))和 ( x , f ( − x ) ) (x,f(-x)) (x,f(−x))关于y轴对称
- 从而 f ( x ) , g ( x ) f(x),g(x) f(x),g(x)关于 y y y轴对称,即 f ( x ) , f ( − x ) f(x),f(-x) f(x),f(−x)关于 y y y轴对称
- 例如:
- f ( x ) = sin ( x ) f(x)=\sin(x) f(x)=sin(x),则 f ( − x ) = sin ( − x ) = − sin x f(-x)=\sin(-x)=-\sin{x} f(−x)=sin(−x)=−sinx和 f ( x ) = sin ( x ) f(x)=\sin(x) f(x)=sin(x)关于 y y y轴对称
- 对于 f ( x ) = cos x f(x)=\cos{x} f(x)=cosx, f ( − x ) = cos ( − x ) f(-x)=\cos{(-x)} f(−x)=cos(−x)= cos x \cos{x} cosx, f ( − x ) , f ( x ) f(-x),f(x) f(−x),f(x)关于 y y y轴对称,即函数 cos x \cos{x} cosx自身关于 y y y轴对称
− f ( x ) , f ( x ) -f(x),f(x) −f(x),f(x)
- 和上面的分析类似,取点分析:若函数 f ( x ) f(x) f(x),上存在 A ( a , f ( a ) ) A(a,f(a)) A(a,f(a)),则函数 − f ( x ) -f(x) −f(x)上一定相应地存在 B ( a , − f ( a ) ) B(a,-f(a)) B(a,−f(a))
- 显然两点关于 x x x轴对称,而 x x x是定义域内的任意点,故而 − f ( x ) -f(x) −f(x)和 f ( x ) f(x) f(x)关于 x x x轴对称
偶函数@奇函数
- 偶函数:若函数 f ( x ) f(x) f(x)的定义域关于原点对称且满足 f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x),则函数 f ( x ) f(x) f(x)是偶函数,显然 f ( x ) f(x) f(x)关于 y y y轴对称
- 若 f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x),那么 f ( − x ) , f ( x ) f(-x),f(x) f(−x),f(x)关于 y y y轴对称就变成了 f ( x ) , f ( x ) f(x),f(x) f(x),f(x)关于 y y y轴对称( f ( x ) f(x) f(x)和 f ( − x ) f(-x) f(−x)重合),即 f ( x ) f(x) f(x)关于 y y y轴对称
- 奇函数:若函数 f ( x ) f(x) f(x)的定义域关于原点对称且满足 f ( − x ) = − f ( x ) f(-x)=-f(x) f(−x)=−f(x),则函数 f ( x ) f(x) f(x)是奇函数,显然 f ( x ) f(x) f(x)关于坐标原点对称
- 可以 f ( x ) f(x) f(x)关于原点对称的图形理解为两部分: f ( x ) f(x) f(x)关于 y y y轴对称的图形和 f ( x ) f(x) f(x)关于 x x x轴对称的图形如果重合,那么 f ( x ) f(x) f(x)就是关于原点对称的奇函数
小结
- The graph of f ( − x ) f(−x) f(−x) is the mirror image of the graph of f ( x ) f(x) f(x) with respect to the vertical axis.
- The graph of − f ( x ) −f(x) −f(x) is the mirror image of the graph of f ( x ) f(x) f(x) with respect to the horizontal axis.
- A function is called even if f ( − x ) = f ( x ) f(−x)=f(x) f(−x)=f(x) for all x x x (For example, cos ( x ) \cos(x) cos(x)).
- A function is called odd if f ( − x ) = − f ( x ) f(−x)=−f(x) f(−x)=−f(x) for all x x x (For example, sin ( x ) \sin(x) sin(x)).
其他翻折变换
关于 y = ± x y=\pm x y=±x对称的直角坐标
- A ( x , y ) A(x,y) A(x,y)关于 y = x y=x y=x的对称点坐标 B ( y , x ) B(y,x) B(y,x)
- A ( x , y ) A(x,y) A(x,y)关于 y − x y-x y−x的对称点坐标 B ( − y , − x ) B(-y,-x) B(−y,−x)
关于 x = u 对称 关于x=u对称 关于x=u对称的函数
-
若 f ( x ) f(x) f(x)关于 x = u x=u x=u对称:
- f ( x ) f(x) f(x)的定义域关于 x = u x=u x=u对称
-
若 x 1 , x 2 x_1,x_2 x1,x2关于 u u u对称,则 x 1 + x 2 = 2 u x_1+x_2=2u x1+x2=2u,反之亦然
- 设 A ( a , f ( a ) ) A(a,f(a)) A(a,f(a))是 f ( x ) f(x) f(x)上的点,则 A A A关于对称轴 x = u x=u x=u的对称点 B ( 2 u − a , f ( a ) ) B(2u-a,f(a)) B(2u−a,f(a))也必然在 f ( x ) f(x) f(x)上
- 从而 f ( 2 u − a ) f(2u-a) f(2u−a)= f ( a ) f(a) f(a)
- 由于 a a a是定义域内的任意点,所以 f ( 2 u − x ) = f ( x ) f(2u-x)=f(x) f(2u−x)=f(x)
- 即,满足:
- 定义域关于 x = u x=u x=u对称
- f ( 2 u − x ) f(2u-x) f(2u−x)= f ( x ) f(x) f(x)
- 的函数是关于 x = u x=u x=u对称的函数
-
例如 y ( x ) = ( x − 1 ) 2 y(x)=(x-1)^2 y(x)=(x−1)2; y ( 2 − x ) = ( ( 2 − x ) − 1 ) 2 = ( 1 − x ) 2 = ( x − 1 ) 2 y(2-x)=((2-x)-1)^2=(1-x)^2=(x-1)^2 y(2−x)=((2−x)−1)2=(1−x)2=(x−1)2,即 y ( x ) = y ( 2 − x ) y(x)=y(2-x) y(x)=y(2−x),对称轴为 u = 1 2 ⋅ 2 = 1 u=\frac{1}{2}\cdot2=1 u=21⋅2=1
- 特别的,偶函数关于 x = 0 x=0 x=0对称, f ( x ) = f ( − x ) f(x)=f(-x) f(x)=f(−x),对称轴 x = u = 0 x=u=0 x=u=0,因为 x + ( − x ) = 2 u = 0 ; u = 0 x+(-x)=2u=0;u=0 x+(−x)=2u=0;u=0
关于 y = v y=v y=v对称的两个函数
- 若 f 1 ( x ) , f 2 ( x ) f_1(x),f_2(x) f1(x),f2(x)在定义域内满足 f 1 ( x ) + f 2 ( x ) = 2 v f_1(x)+f_2(x)=2v f1(x)+f2(x)=2v,则 f 1 ( x ) , f 2 ( x ) f_1(x),f_2(x) f1(x),f2(x)关于 y = v y=v y=v对称
相关文章:

EM@坐标@函数@图象的对称和翻折变换
文章目录 abstract翻折变换关于坐标轴翻折 f ( − x ) , f ( x ) f(-x),f(x) f(−x),f(x) − f ( x ) , f ( x ) -f(x),f(x) −f(x),f(x) 偶函数奇函数小结 其他翻折变换关于 y x y\pm x yx对称的直角坐标 关于 x u 对称 关于xu对称 关于xu对称的函数关于 y v yv yv对称的两…...

Python之json模块
JSON (JavaScript Object Notation),由 RFC 7159 (它取代了 RFC 4627) 和 ECMA-404 指定,是一个受 JavaScript 的对象字面值句法启发的轻量级数据交换格式。JSON独立于编程语言的文本格式来存储和表示数据,现在大部分的数据传输基本使用的都是…...
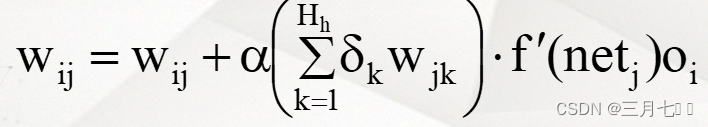
机器学习---BP算法
1. 多级网络 层号确定层的高低:层号较小者,层次较低,层号较大者,层次较高。 输入层:被记作第0层。该层负责接收来自网络外部的信息。 第j层:第j-1层的直接后继层(j>0)ÿ…...

继苹果、联发科后,传高通下一代5G芯片将由台积电以3纳米代工
台积电3纳米又有重量级客户加入。市场传出,继苹果、联发科之后,手机芯片大厂高通下一代5G旗舰芯片也将交由台积电以3纳米生产,最快将于10月下旬发表,成为台积电3纳米第三家客户。 针对相关传闻,至昨日(25日…...
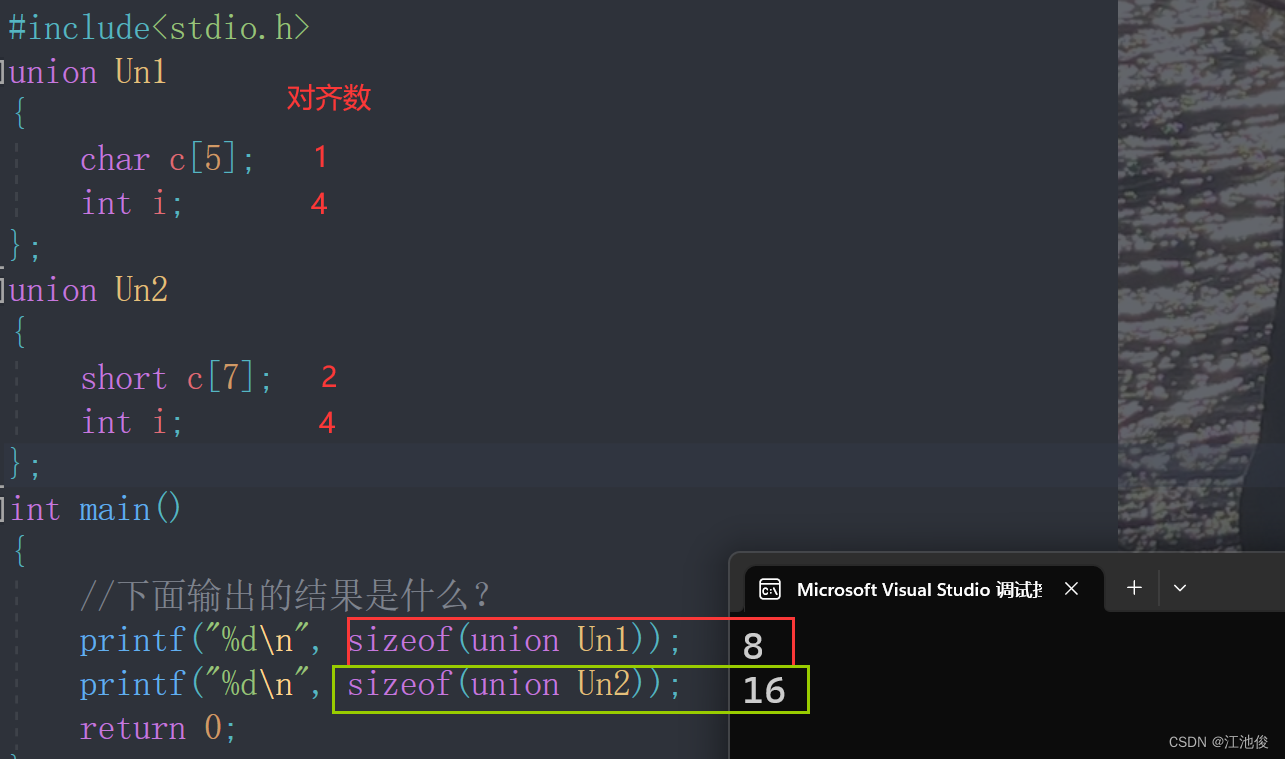
【自定义类型】--- 位段、枚举、联合
💓博客主页:江池俊的博客⏩收录专栏:C语言进阶之路👉专栏推荐:✅C语言初阶之路 ✅数据结构探索💻代码仓库:江池俊的代码仓库🎉欢迎大家点赞👍评论📝收藏⭐ 文…...
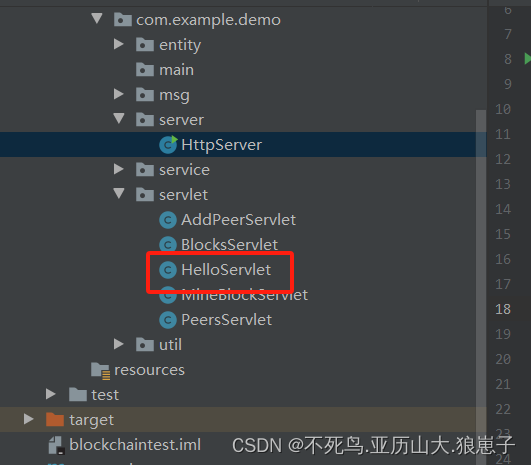
区块链(9):java区块链项目的Web服务实现之实现web服务
1 引入pom依赖 <dependency><groupId>org.eclipse.jetty</groupId><artifactId>jetty-server</artifactId><version>9.4.8.v20171121</version></dependency><dependency><groupId>org.eclipse.jetty</groupId…...

【CV】各种库安装报错及解决办法
目录 1.Error:Cannot unpack file… 1.Error:Cannot unpack file… 使用命令pip install -i https://pypi.tuna.tsinghua.edu.cn/simple --trusted-host pypi.tuna.tsinghua.edu.cn 包名安装 参考:解决Python使用pip安装库文件出现“Error&a…...
【算法系列篇】哈希表
文章目录 前言1. 两数之和1.1 题目要求1.2 做题思路1.3 Java代码实现 2. 判断是否为字符重排2.1 题目要求2.2 做题思路2.3 Java代码实现 3. 存在重复元素3.1 题目要求3.2 做题思路3.3 Java代码实现 4. 存在重复元素II4.2 题目要求4.2 做题思路4.3 Java代码实现 5. 字母异位词分…...
计算机视觉——飞桨深度学习实战-起始篇
后面我会直接跳到实战项目,将计算机视觉的主要任务和目标都实现一遍,但是需要大家下去自己多理解和学习一下。例如,什么是深度学习,什么是计算机视觉,什么是自然语言处理,计算机视觉的主要任务有哪些&#…...

vscode中运行脚手架项目报表
必选在cmd页面里面安装脚手架离谱啊,不然无法执行npm命令啊 vscode运行vue项目_小何不秃头06的博客-CSDN博客 finereport激活成功 - 帆软 (fanruan.com)...

中睿天下荣获2023全国智能驾驶测试赛车联网安全比赛第一名
9月24日,由工业和信息化部、公安部、交通运输部、中国科学技术协会、北京市人民政府共同主办的2023世界智能网联汽车大会展览会在北京闭幕。同期举行的全国智能驾驶测试赛(京津冀赛区)宣布比赛结果,中睿天下凭借过硬的产品实力&am…...
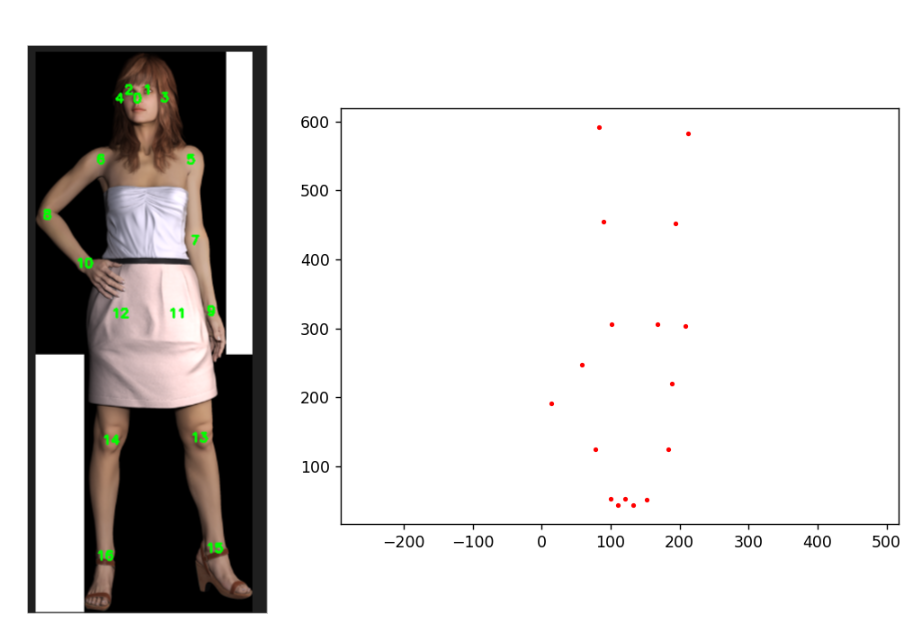
opencv图像数组坐标系
在OpenCV的Python接口(cv2)中,加载的图像数组遵循以下坐标系和方向约定: 1. **坐标系:** OpenCV的坐标系遵循数学中的坐标系,原点(0, 0)位于图像的左上角。横轴(X轴&…...
zookeeper mac安装
目录 1.下载zookeeper安装包 2.解压安装包 3.修改配置文件 4.启动服务端 5.启动客户端 这边工作中用到了zookeeper组件,但自己独立安装弄的不太多,这边本机mac装一个做测试使用 以下是安装记录,可以作为参考 从以下链接zookeeper版本列…...

js生成随机16进制数
在JavaScript中,可以使用以下的代码来生成一个100位的随机十六进制数: function generateRandomHex(length) {var result ;var characters 0123456789abcdef;for (var i 0; i < length; i) {result characters.charAt(Math.floor(Math.random() …...
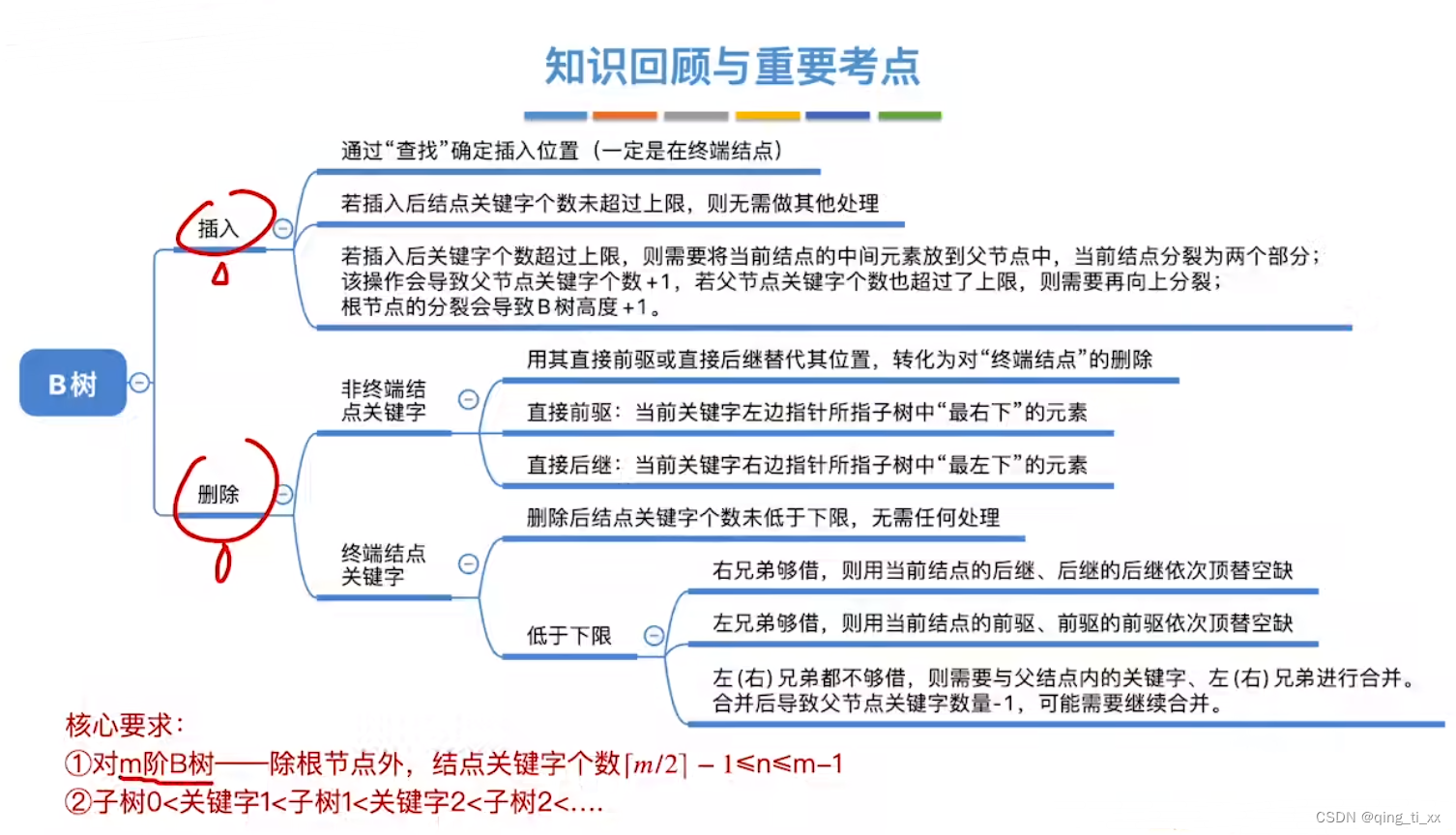
第七章 查找 八、B树
目录 一、定义 二、B树的核心特性 1、B树各个结点的子树数和关键字数 2、子树高度 3、关键字的值 4、B树高度 三、B树的插入 四、B树的删除 一、定义 B树,又称多路平衡查找树,B树中所有结点的孩子个数的最大值称为B树的阶,通常用m表示…...

Vue以及整合ElementUI
初始化vue项目 #vue 脚手架使用 webpack 模板初始化一个 appname 项目 vue init webpack appname启动 vue 项目 #项目的 package.json 中有 scripts,代表我们能运行的命令 npm start npm run dev #启动项目 npm run build:将项目打包项目结构 运行流程…...
免费、丰富、便捷的资源论坛——Yiove论坛,包括但不限于阿里云盘、夸克云盘、迅雷云盘等等
引言 目前资源的数量达到了60000,六万多的资源意味着在这里几乎可以找到任何你想要的资源。 当然,资源并不是论坛的全部,其中还包括了技术交流、福利分享、最新资讯等等。 传送门:YiOVE论坛 - 一个有资源有交流,有一…...

1.3 互联网的组成
思维导图: 前言: 我的笔记: #### 一、总览 - **互联网的结构**: - 具有全球覆盖和复杂的拓扑结构。 - 即便结构复杂,还是可以从工作方式上简化为两大部分:边缘部分和核心部分。 #### 二、边缘部分 -…...
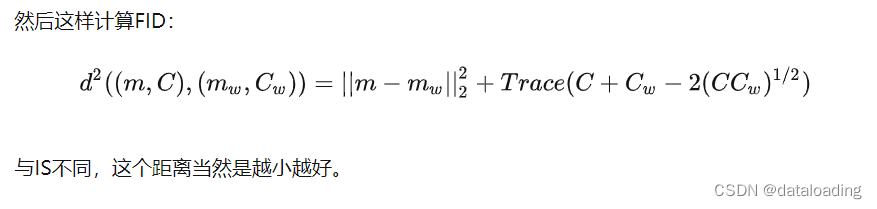
【机器学习】熵和概率分布,图像生成中的量化评估IS与FID
详解机器学习中的熵、条件熵、相对熵、交叉熵 图像生成中常用的量化评估指标通常有Inception Score (IS)和Frchet Inception Distance (FID) Inception Score (IS) 与 Frchet Inception Distance (FID) GAN的量化评估方法——IS和FID,及其pytorch代码...
Vue3.0跨端Web SDK访问微信小程序云储存,文件上传路径不存在/文件受损无法显示问题(已解决)
整理需求: 需要vue3.0作为pc端的后台管理来连接微信小程序客户端需要Web SDK的引入,实现vue3.0接入云开发环境需要以云环境作为线上服务器,将vue3.0上传的本地文件通过云环境进入云储存,并将文件在云端生成云端快捷访问路径及htt…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
