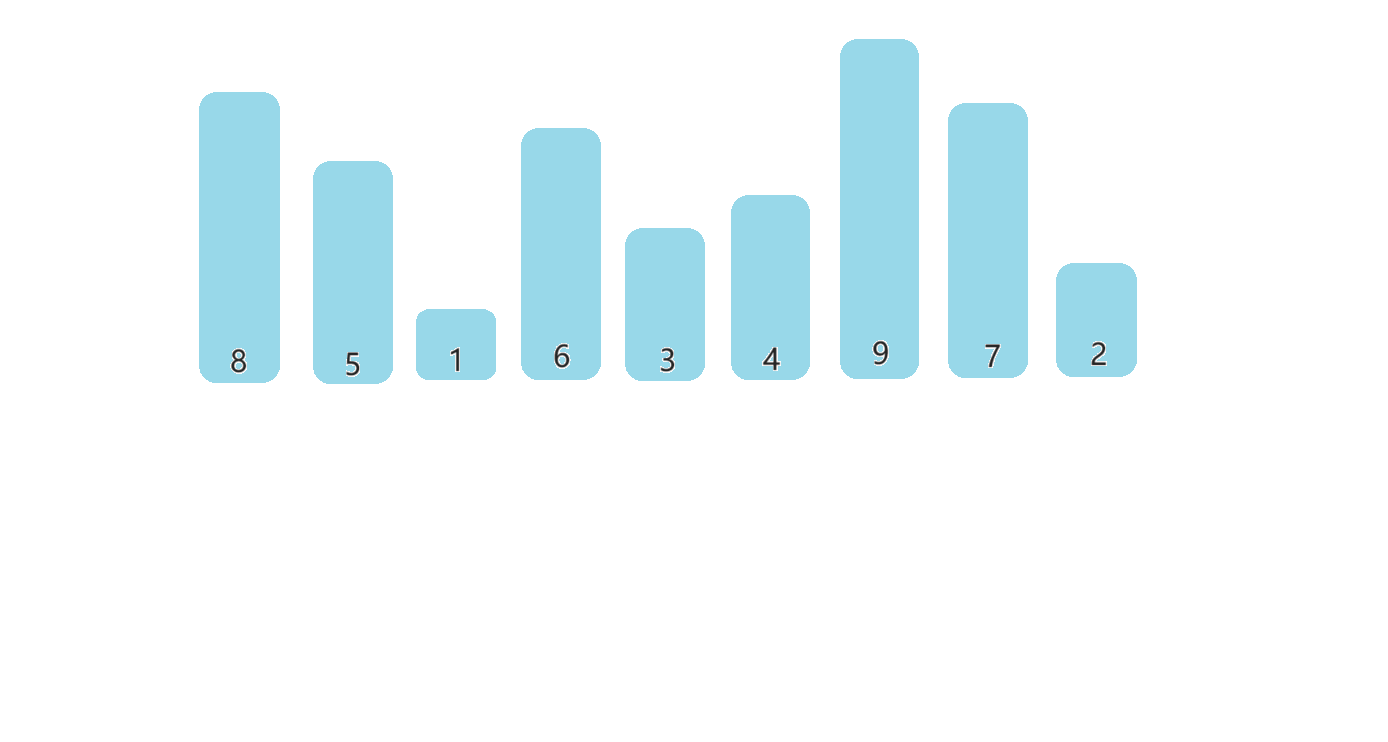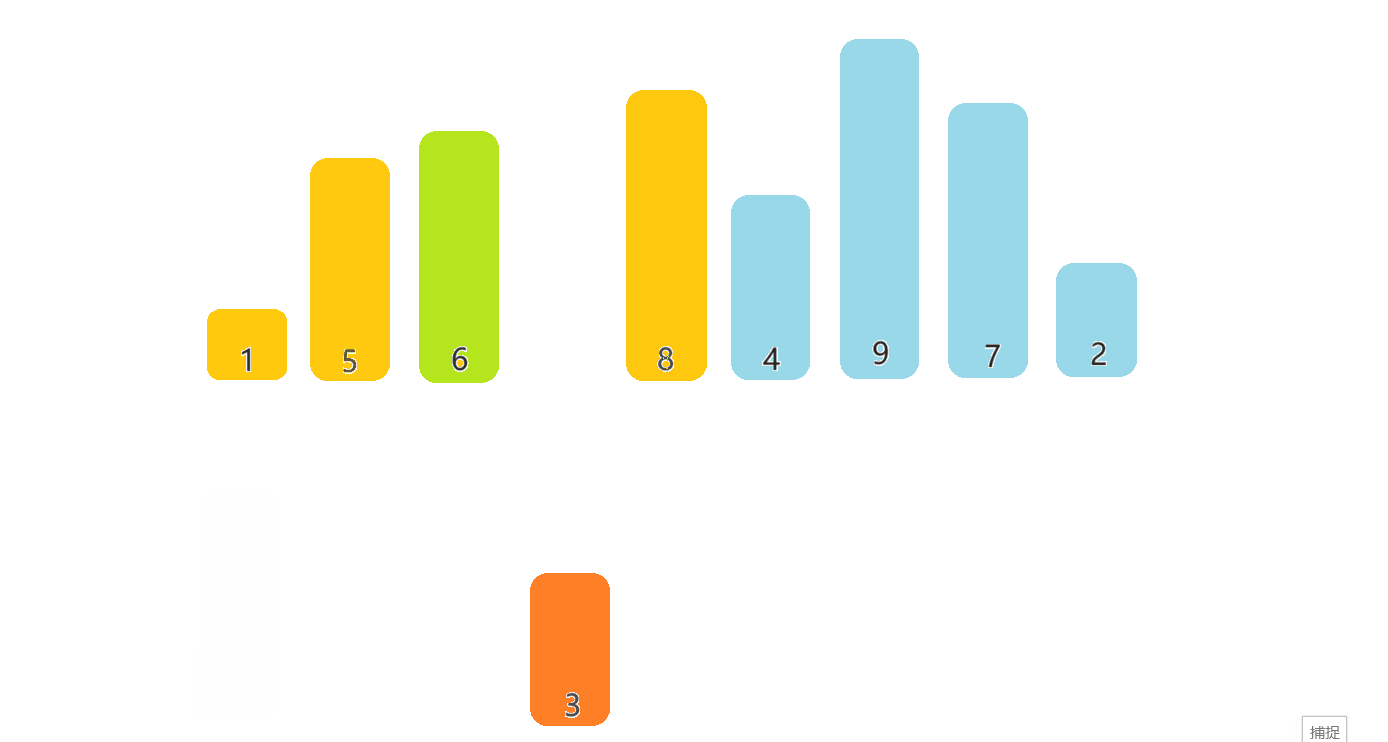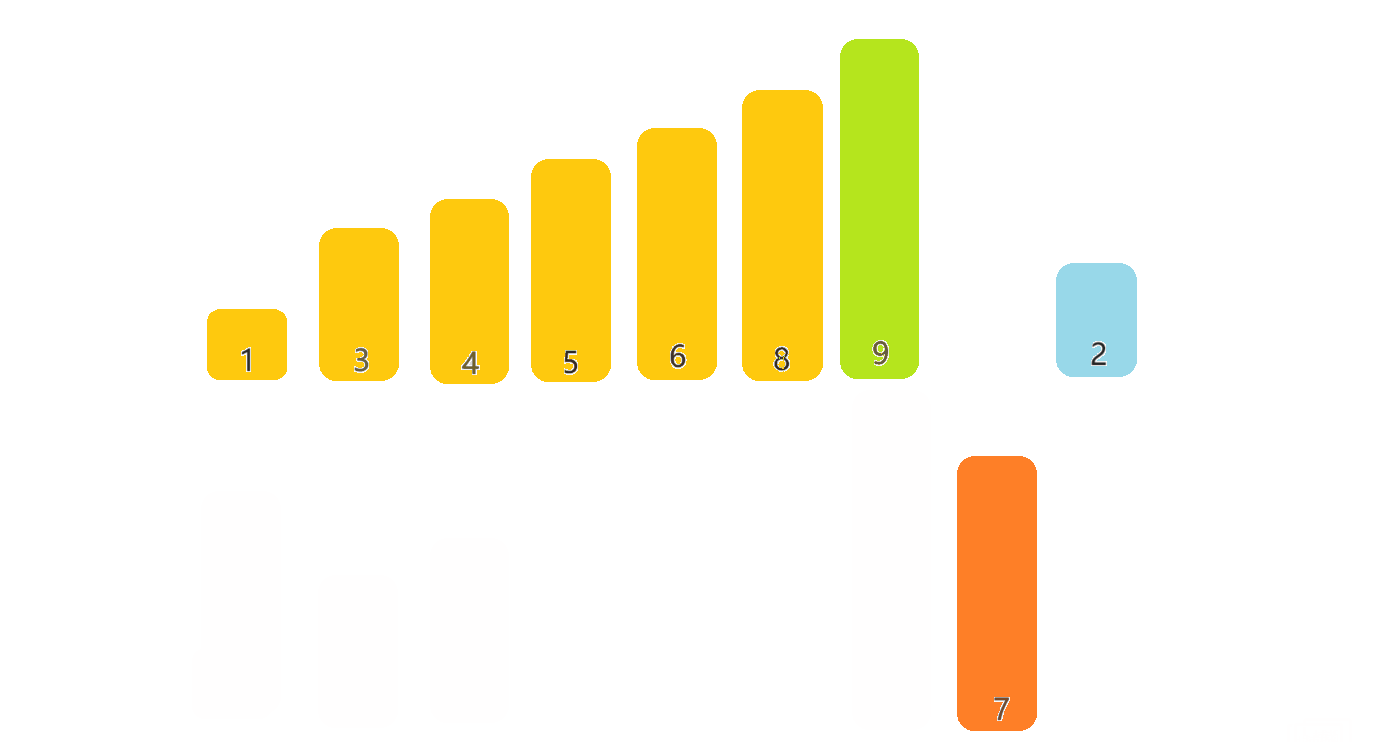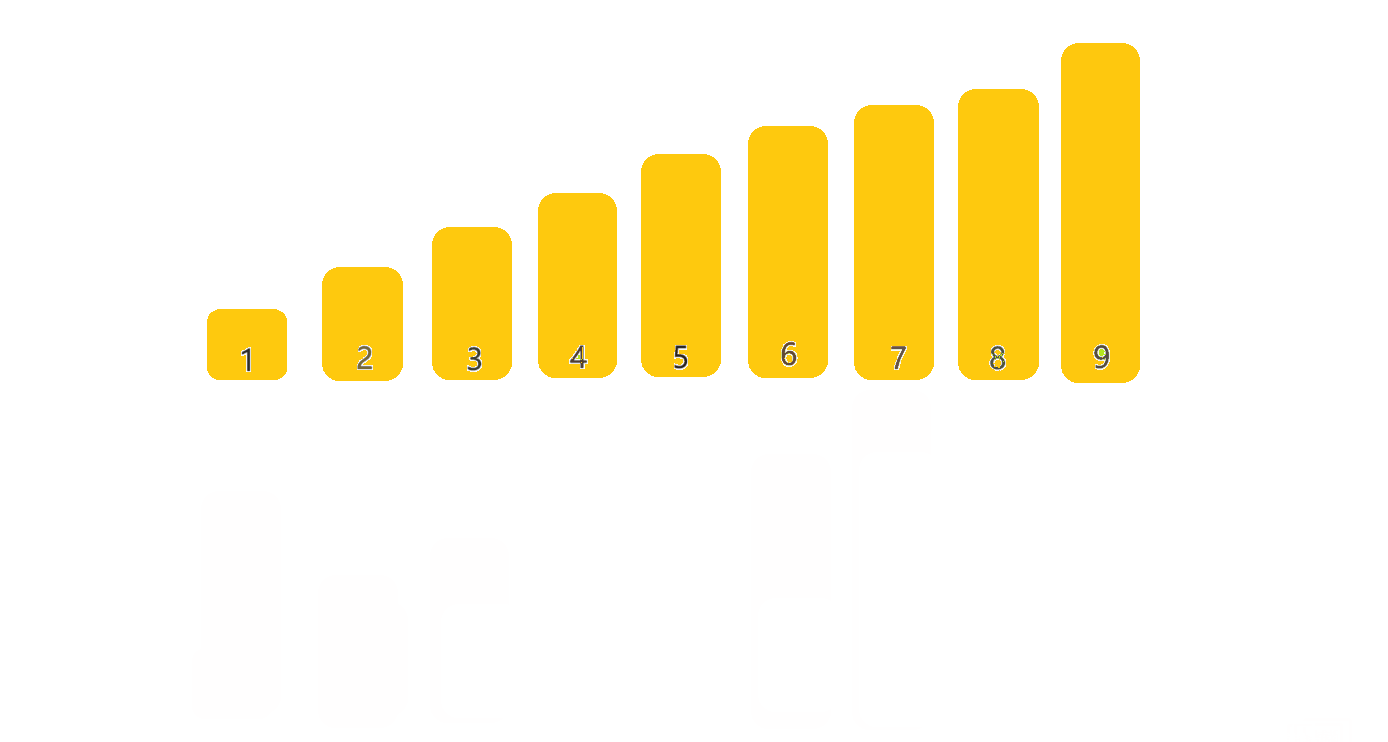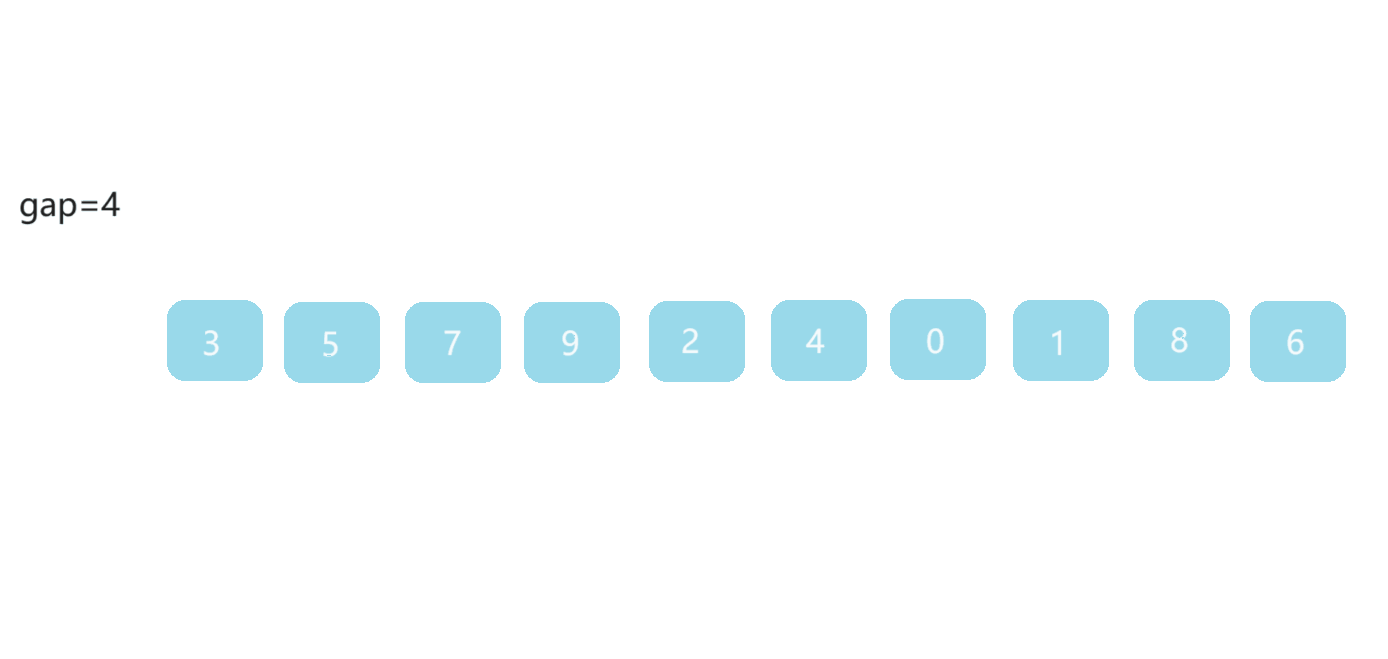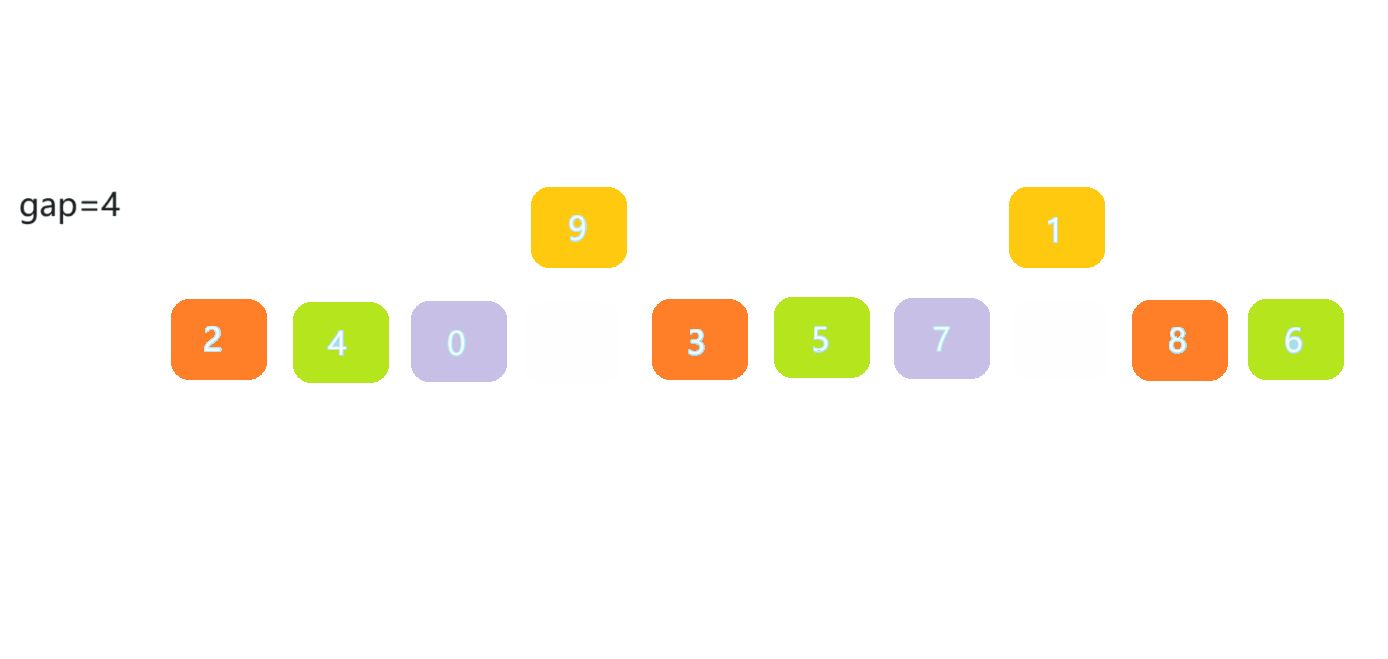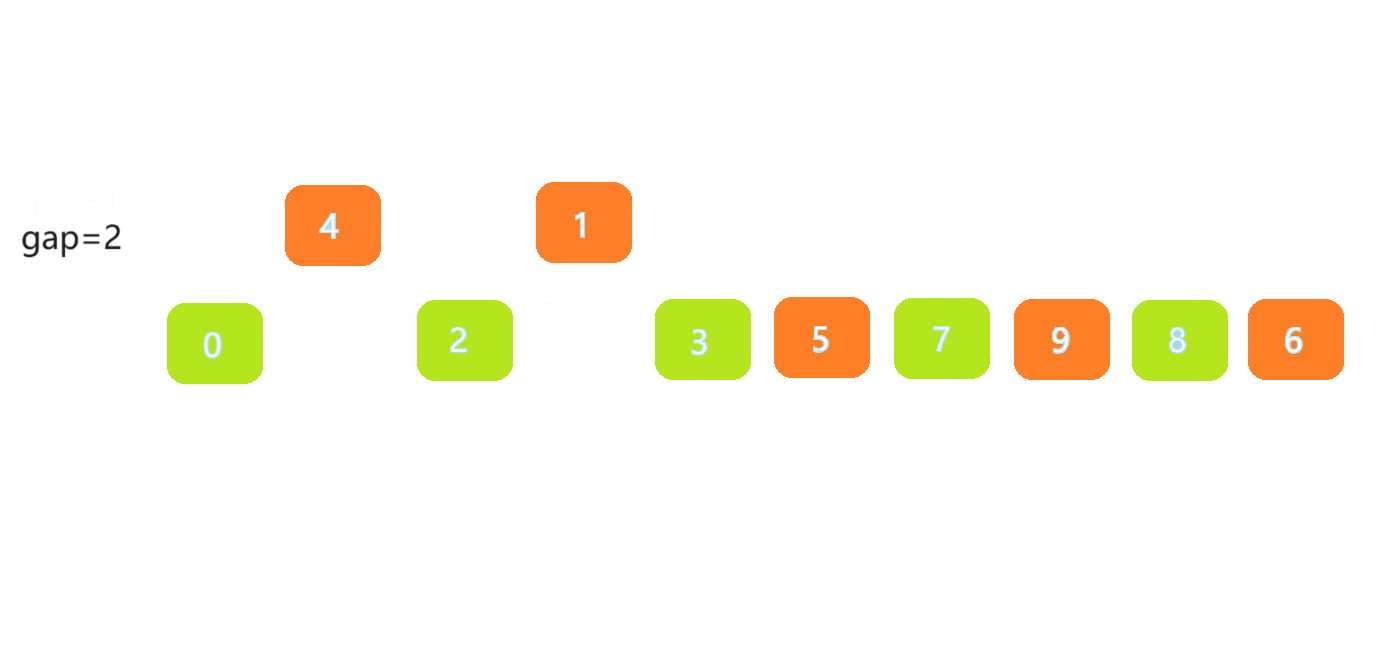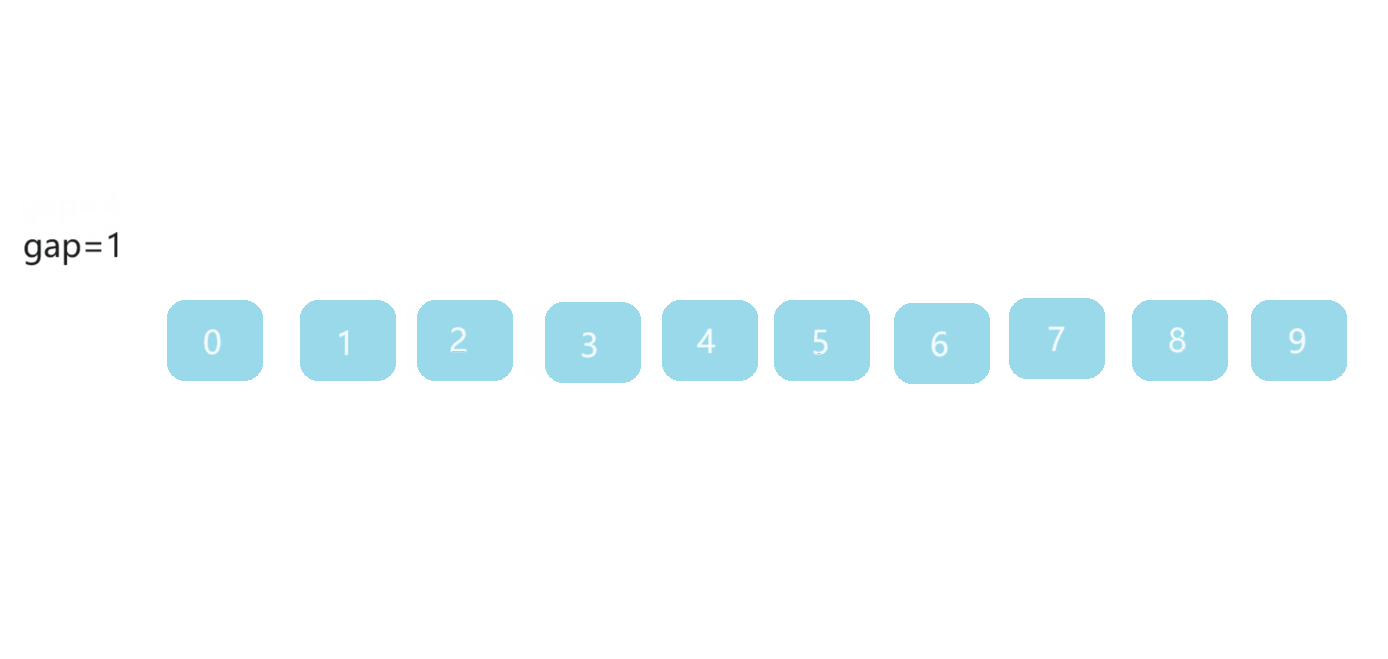【数据结构】排序之插入排序和选择排序

🔥博客主页:小王又困了
📚系列专栏:数据结构
🌟人之为学,不日近则日退
❤️感谢大家点赞👍收藏⭐评论✍️
目录
一、排序的概念及其分类
📒1.1排序的概念
📒1.2排序的分类
二、插入排序
📒2.1直接插入排序
🎀2.1.1直接插入排序的思想
🎀2.1.2排序步骤
🎀2.1.3代码实现
🎀2.1.4直接插入排序的特点
📒2.2希尔排序
🎀2.2.1希尔排序法的基本思想
🎀2.2.2排序步骤
🎀2.2.3代码实现
🎀2.2.4希尔排序的特点
三、选择排序
📒3.1直接选择排序
🎀3.1.1直接选择排序的思想
🎀3.1.2排序步骤
🎀3.1.3代码实现
🎀3.1.4直接选择排序的特点
📒3.2堆排序
🎀3.2.1堆排序的思想
🎀3.2.2排序步骤
🎀3.2.3代码实现
🎀3.2.4堆排序的特点
🗒️前言:
排序是我们数据结构学习中很重要的章节,我们在生活中买东西都会挑选更好的,点外卖会选评分高的等等,这些都需要用到排序。接下来我们将会学习常见的排序算法。
一、排序的概念及其分类
📒1.1排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次 序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排 序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
📒1.2排序的分类

二、插入排序
📒2.1直接插入排序
🎀2.1.1直接插入排序的思想
把待排序的数据按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的数据插入完为止,得到一个新的有序序列 。 实际中我们玩扑克牌时,就用了插入排序的思想。
注意:数组中除了第一个元素(默认有序),其余所有元素都看作待插入数据。
🎀2.1.2排序步骤
- 将有序数据的最后一个元素的下标记为 end,则第一个待插入元素的下标为 end+1,记作 tmp
- 将 tmp 与有序数据从后向前依次比较
- 如果 tmp < a[end],就将 a[end] 向后移动,end--,再去找下一位进行比较
- 直到 tmp > a[end] 或者 end < 0,将 tmp 插入到 end+1 的位置
- 重复步骤,就可以实现排序
🎀2.1.3代码实现
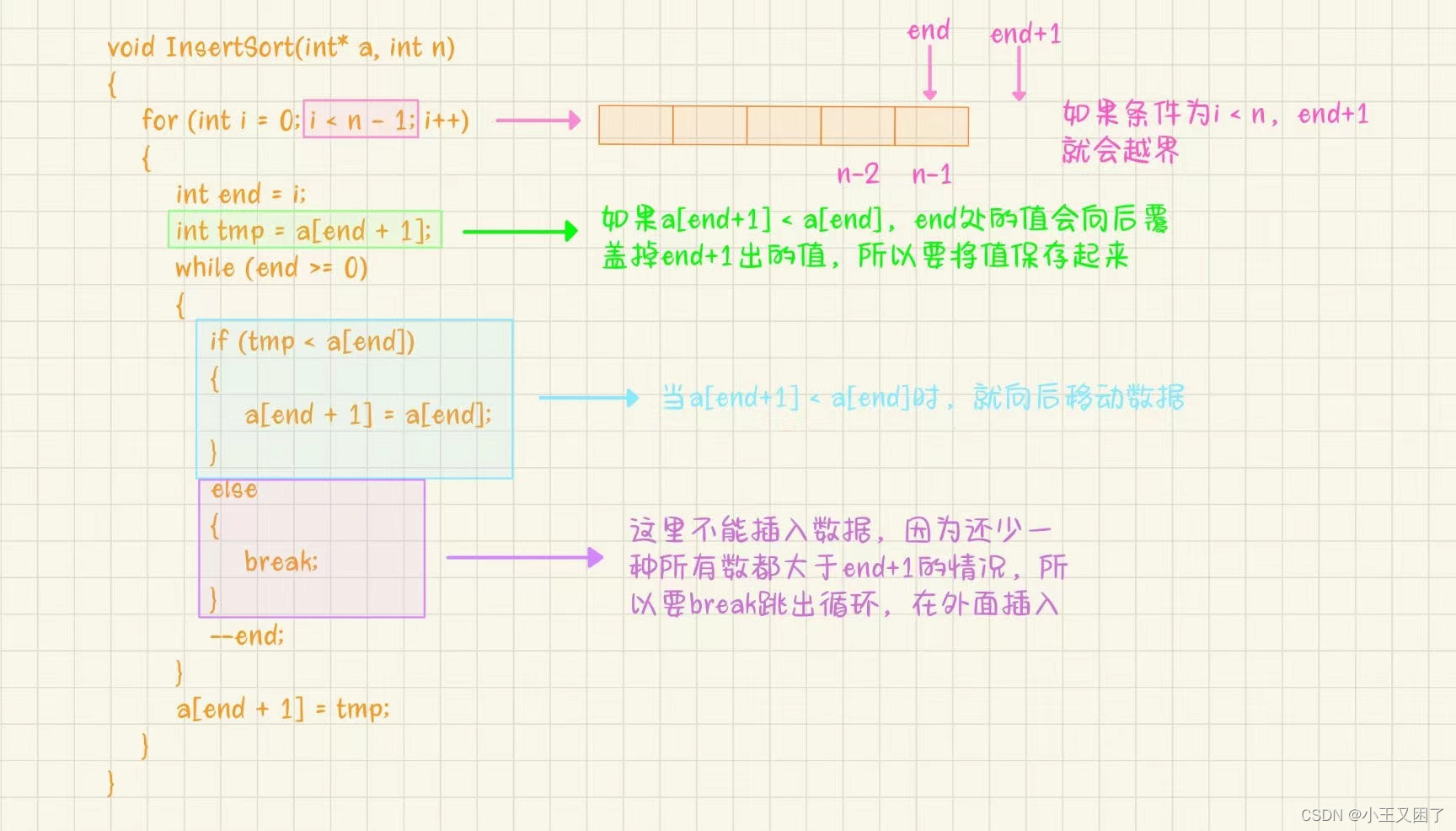
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];}else{break;}--end;}a[end + 1] = tmp;}
}
🎀2.1.4直接插入排序的特点
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
📒2.2希尔排序
🎀2.2.1希尔排序法的基本思想
先选定一个整数,把待排序文件中所有记录分成个组,所有距离为3的数据分在同一组内,并对每一组内的数据进行排序。然后,重复上述分组和排序的工作。当距离=1时,所有数据在统一组内排好序。
希尔排序分为两步:
- 预排序
- 直接插入排序
当元素集合越接近有序,直接插入排序的效率很高,希尔排序就是通过预排序使元素集合接近有序,再进行直接插入排序,这样大大提高了效率。
🎀2.2.2排序步骤
- 选取一个合适的 gap 作为间距
- 将间距为 gap 的数据分为一组,分成 gap 组
- 每一组数据都进行直接插入排序,使数据接近有序
- 不断缩小间距,当 gap==1 时,数据进行直接插入排序,实现排序
🎀2.2.3代码实现
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}将 i+=gap 改为 i++, 将分组排序,变为多组并排,减少了循环。
gap = gap / 3 + 1 的目的是保证 gap 最后的值为1.
🎀2.2.4希尔排序的特点
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算。
- 空间复杂度:O(1)
- 稳定性:不稳定
三、选择排序
📒3.1直接选择排序
🎀3.1.1直接选择排序的思想
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
🎀3.1.2排序步骤
- 先遍历一遍数组,找到最大的数和最小的数,记住它们的下标
- 将最小的数交换到数组的左边,最大的数交换到数组的右边
- begin++,end--,重复上述步骤,即可实现排序
🎀3.1.3代码实现
void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int min = begin, max = begin;for (int i = begin + 1; i <= end; i++){if (a[min] > a[i]){min = i;}if (a[max] < a[i]){max = i;}}Swap(&a[min], &a[begin]);if (max == begin){max = min;}Swap(&a[max], &a[end]);begin++;end--;}
}我们要注意,当 a[max] 在数组元素的第一个,进行 Swap(&a[min], &a[begin]) 后,最大的元素的位置就发生了改变,要及时修改 max。
🎀3.1.4直接选择排序的特点
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
📒3.2堆排序
🎀3.2.1堆排序的思想
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
🎀3.2.2排序步骤
- 将待排序的数据构造成一个大堆,当前堆的根节点(堆顶)就是该组数组中最大的元素;
- 将堆顶元素和最后一个元素交换,将剩下的节点重新构造成一个大堆;
- 重复步骤2,每次循环构建都能找到当前堆中的最大值,并通过交换的方式把它放到该大堆的尾部,直至所有元素全部有序
🎀3.2.3代码实现
void HeapSort(int* a, int n)
{//第一步:建大堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}//第二步:堆删除思想进行排序(依次选数,调堆)for (int i = n - 1; i > 0; i--){Swap(&a[0], &a[i]);AdjustDown(a, i , 0);}
}
void AdjustDown(HPDataType* a, int n, int parent)
{//默认左孩子是较小的int child = parent * 2 + 1;while (child < n){// 找出小的那个孩子if (child + 1 < n && a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{break;}}
}
🎀3.2.4堆排序的特点
- 堆排序使用堆来选数,效率就高了很多。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(1)
- 稳定性:不稳定
本次的内容到这里就结束啦。希望大家阅读完可以有所收获,同时也感谢各位读者三连支持。文章有问题可以在评论区留言,博主一定认真认真修改,以后写出更好的文章。你们的支持就是博主最大的动力。
相关文章:
【数据结构】排序之插入排序和选择排序
🔥博客主页:小王又困了 📚系列专栏:数据结构 🌟人之为学,不日近则日退 ❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、排序的概念及其分类 📒1.1排序的概念 📒1.2排序…...

6.html表单
HTML表单(HTML form)是网页中用于收集用户输入数据的一种方式。表单由多个表单元素组成,通常包括输入框,复选框,单选按钮,下拉列表和提交按钮等。 HTML表单元素的基本结构如下: <form acti…...

【python学习第11节:numpy】
文章目录 一,numpy(上)1.1基础概念1.2数组的属性1.3数组创建1.4 类型转换1.5ndarry基础运算(上)矢量化运算1.6拷贝和视图1.6.1完全不复制1.6.2视图或浅拷贝1.6.3深拷贝 1.7索引,切片和迭代1.7.1一维数组1.7…...

Eclipse 主网即将上线迎空投预期,Zepoch 节点或成受益者?
目前,Zepoch 节点空投页面中,模块化 Layer2 Rollup 项目 Eclipse 出现在其空投列表中。 配合近期 Eclipse 宣布了其将由 SVM 提供支持的 Layer2 主网架构,并将在今年年底上线主网的消息后,不免引发两点猜测:一个是 Ecl…...
 | 输入输出)
JavaSE | 初识Java(四) | 输入输出
基本语法 System.out.println(msg); // 输出一个字符串, 带换行 System.out.print(msg); // 输出一个字符串, 不带换行 System.out.printf(format, msg); // 格式化输出 println 输出的内容自带 \n, print 不带 \n printf 的格式化输出方式和 C 语言的 printf 是基本一致的 代码…...

车牌超分辨率:License Plate Super-Resolution Using Diffusion Models
论文作者:Sawsan AlHalawani,Bilel Benjdira,Adel Ammar,Anis Koubaa,Anas M. Ali 作者单位:Prince Sultan University 论文链接:http://arxiv.org/abs/2309.12506v1 内容简介: 1)方向:图像超分辨率技术…...
如何制作在线流程图?6款在线工具帮你轻松搞定
流程图,顾名思义 —— 用视觉化的方式来描述一种过程或流程。它可以应用于各种领域,从业务流程,算法,到计算机程序等。然而,在创建流程图时,可能会遇到许多问题或者困惑,如缺乏专业的设计技能&a…...

反SSDTHOOK的另一种思路-0环实现自己的系统调用
反SSDTHOOK的另一种思路-0环实现自己的系统调用 大家都知道我们在应用层使用系统api除了gdi相关的都会走中断门或者systementer进0环然后在走ssdt表去执行0环的函数 这也就导致了ssdthook可以挡下大部分的api调用,那如果我们进0环走另外一条路线的话不通过ssdt就可…...
)
Certbot签发和续费泛域名SSL证书(通过DNS TXT记录来验证域名有效性)
我们在使用let’s encrypt获取免费的HTTPS证书的时候,let’s encrypt需要对域名进行验证,以确保域名是你自己的 之前用默认的文件验证方式总有奇怪的问题导致失败,我也是很无奈,于是改用验证DNS-TXT记录的方式来验证,而…...

PY32F003F18之RTC
一、RTC振荡器 PY32F003F18实时时钟的振荡器是内部RC振荡器,频率为32.768KHz。它也可以使用HSE时钟,不建议使用。HAL库提到LSE振荡器,但PY32F003F18实际上没有这个振荡器。 缺点:CPU掉电后,需要重新配置RTCÿ…...

redis主从从,redis-7.0.13
redis主从从,redis-7.0.13 下载redis安装redis安装redis-7.0.13过程报错1、没有gcc,报错2、没有python3,报错3、[adlist.o] 错误 127 解决安装报错安装完成 部署redis 主从从结构redis主服务器配置redis启动redis登录redisredis默认是主 redi…...

力扣-338.比特位计数
Idea 直接暴力做法:计算从0到n,每一位数的二进制中1的个数,遍历其二进制的每一位即可得到1的个数 AC Code class Solution { public:vector<int> countBits(int n) {vector<int> ans;ans.emplace_back(0);for(int i 1; i < …...
【Leetcode】 17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 示例 1: 输入:digits "23" 输出&…...
洛谷P1102 A-B 数对题解
目录 题目A-B 数对题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示传送门 代码解释亲测 题目 A-B 数对 题目背景 出题是一件痛苦的事情! 相同的题目看多了也会有审美疲劳,于是我舍弃了大家所熟悉的 AB Problem,改用 …...
【Linux进行时】进程地址空间
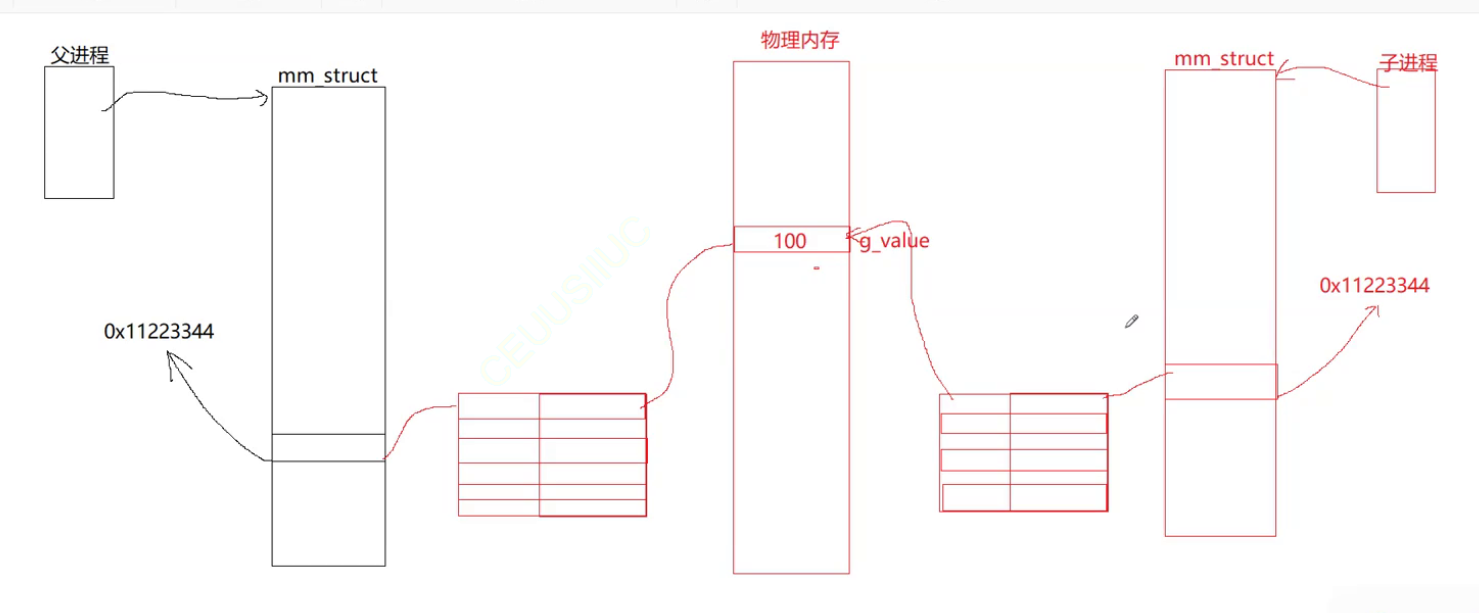
进程地址空间 例子引入: 我们在讲C语言的时候,老师给大家画过这样的空间布局图,但是我们对它不了解 我们写一个代码来验证Linux进程地址空间 #include<stdio.h> #include<assert.h> #include<unistd.h> int g_value100; …...
批量将文件名称符合要求的文件自动复制到新文件夹:Python实现
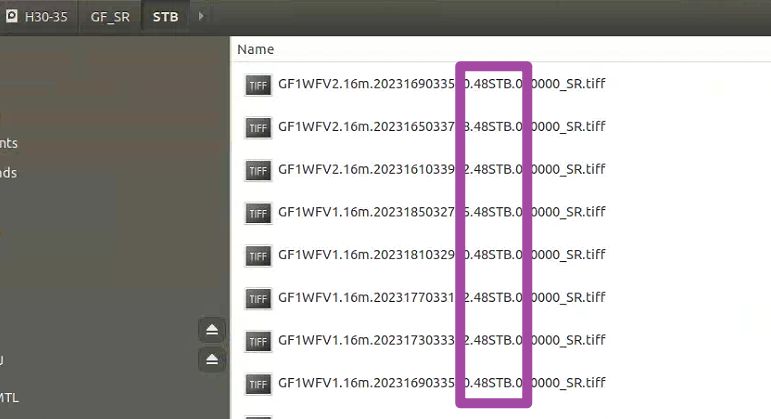
本文介绍基于Python语言,读取一个文件夹,并将其中每一个子文件夹内符合名称要求的文件加以筛选,并将筛选得到的文件复制到另一个目标文件夹中的方法。 本文的需求是:现在有一个大的文件夹,其中含有多个子文件夹&#x…...
TensorFlow入门(一、环境搭建)
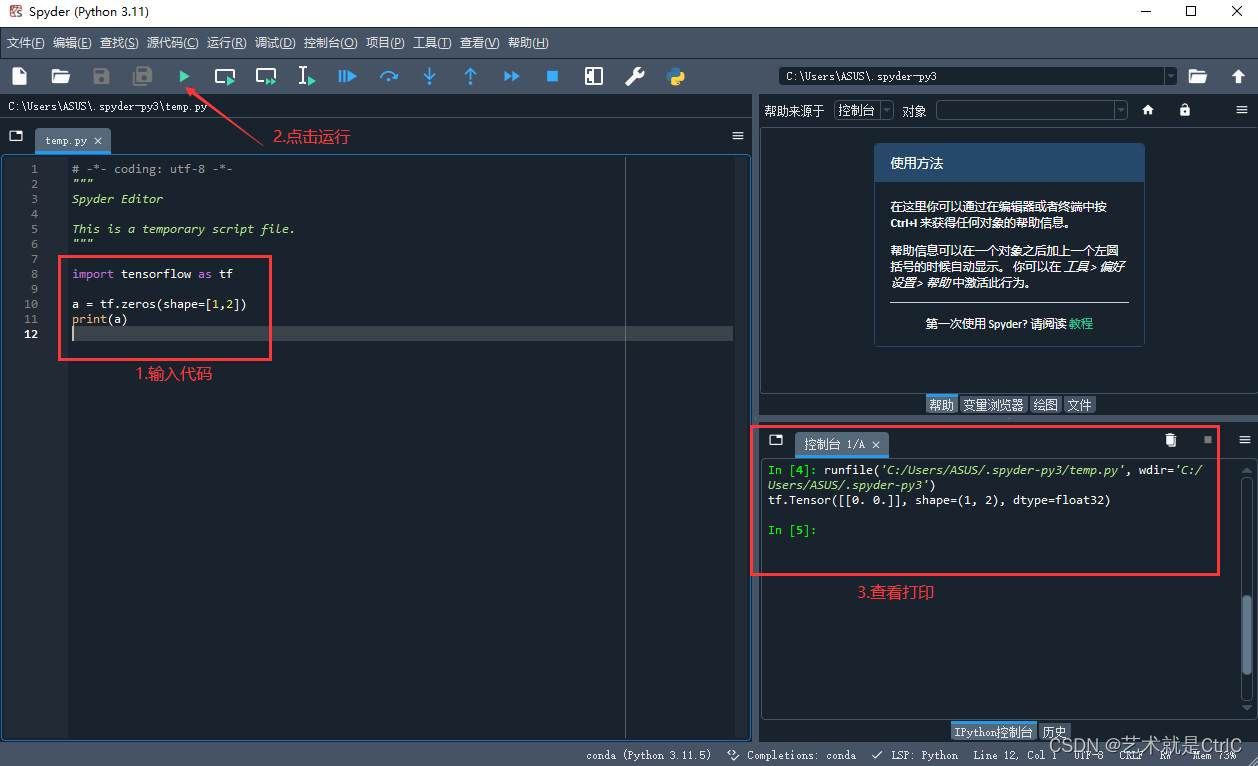
一、下载安装Anaconda 下载地址:http://www.anaconda.comhttp://www.anaconda.com 下载完成后运行exe进行安装 二、下载cuda 下载地址:http://developer.nvidia.com/cuda-downloadshttp://developer.nvidia.com/cuda-downloads 下载完成后运行exe进行安装 安装后winR cmd进…...
90、Redis 的 value 所支持的数据类型(String、List、Set、Zset、Hash)---->Hash 相关命令
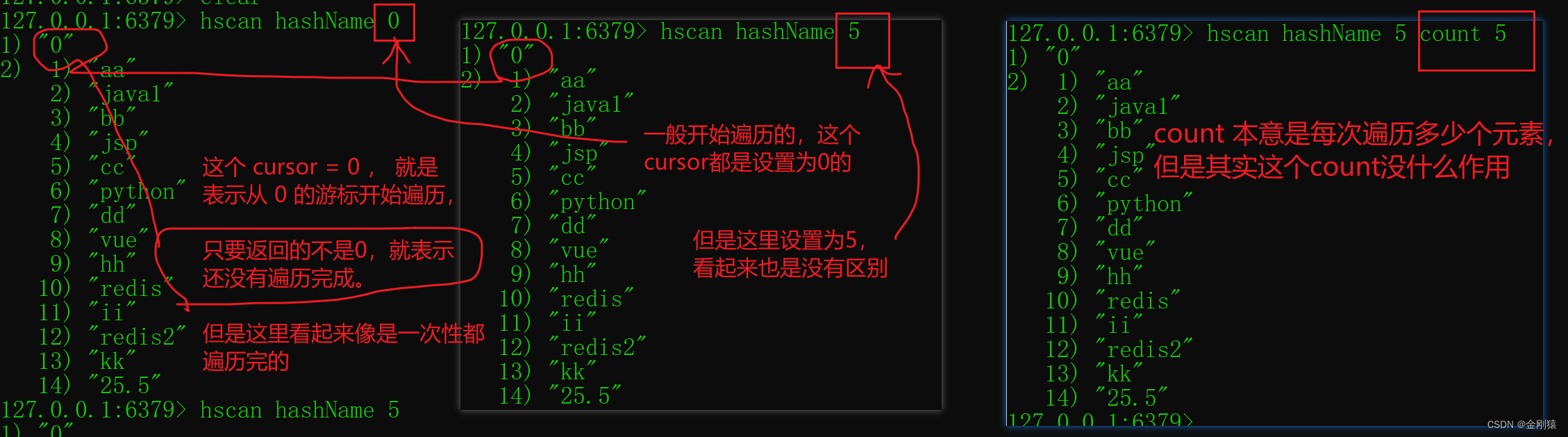
本次讲解要点: Hash 相关命令:是指value中的数据类型 启动redis服务器: 打开小黑窗: C:\Users\JH>e: E:>cd E:\install\Redis6.0\Redis-x64-6.0.14\bin E:\install\Redis6.0\Redis-x64-6.0.14\bin>redis-server.exe red…...

我开源了一个加密算法仓库,支持18种算法!登录注册业务可用!
文章目录 仓库地址介绍安装用法SHA512HMACBcryptScryptAESRSAECC 仓库地址 仓库地址:https://github.com/palp1tate/go-crypto-guard 欢迎star和fork! 介绍 此存储库包含用 Go 编写的全面的密码哈希库。该库支持多种哈希算法,它允许可定制…...
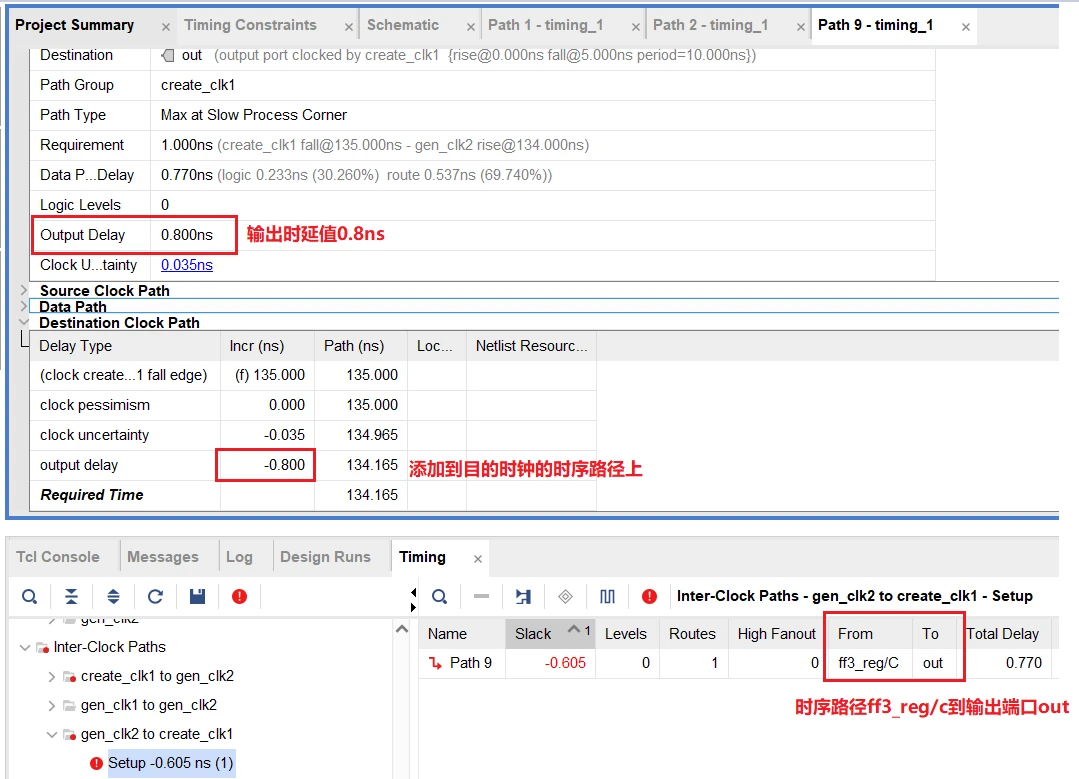
FPGA设计时序约束二、输入延时与输出延时
目录 一、背景 二、set_input_delay 2.1 set_input_delay含义 2.2 set_input_delay参数说明 2.3 使用样例 三、set_output_delay 3.1 set_output_delay含义 3.2 set_output_delay参数说明 3.3 使用样例 四、样例工程 4.1 工程代码 4.2 时序报告 五、参考资料 一、…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...