代码随想录 动态规划 13
300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列
思路:由题意得知,子序列是可以删除数组中的元素的,即一段长为s的序列的最长子序列,可能与若干个元素都无关,因此 长度为s的序列的最长子序列的状态依赖于在这之前的所有长度为1,2,3,。。。s-1的状态。转移方程,由于要求的是最长严格递增子序列,那么不难想到,如果当前的元素比遍历到的元素的元素大,那么就可以将其放到该元素的后面,形成一个严格递增子序列。既然如此,dp数组的定义就定义为,dp[i] 为 以 nums[i]结尾的最长子序列,转移方程为 if nums[i] > nums[j], dp[i] = max(dp[i], dp[j] + 1),初始化为1. 使用result来记录dp数组中的最大值。
class Solution:def lengthOfLIS(self, nums: List[int]) -> int:dp = [1 for _ in range(len(nums))]result = 1for i in range(1, len(dp)):for j in range(i):if nums[i] > nums[j]:dp[i] = max(dp[i], dp[j] + 1)result = max(dp[i], result)return result674. 最长连续递增序列
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
思路:与上一题类似,dp[i]的定义为 以nums[i]为结尾的连续递增子序列长度,转移方程为,当nums[i] > nums[i-1], dp[i] = dp[j] + 1, 以result记录dp数组最大值
class Solution:def findLengthOfLCIS(self, nums: List[int]) -> int:dp = [1 for _ in range(len(nums))]result = 1for i in range(1, len(dp)):if nums[i] > nums[i-1]:dp[i] = dp[i-1] + 1result = max(dp[i], result)return result
718. 最长重复子数组
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
思路:设置dp[i][j] 为 nums1 前i -1个元素 和 nums2 前 j -1个元素 的公共最长重复子数组,那么转移方程为 if nums1[i-1] == nums2[j-1] , dp[i][j] = dp[i-1][j-1], 由于dp数组的设置,遍历时由1开始,len(nums1)+1 结束 (左闭右开)
二维dp
class Solution:def findLength(self, nums1: List[int], nums2: List[int]) -> int:dp = [[0] * (len(nums2) + 1) for _ in range(len(nums1) + 1)]result = 0for i in range(1, len(nums1) + 1):for j in range(1, len(nums2) + 1):if nums1[i-1] == nums2[j-1]:dp[i][j] = dp[i-1][j-1] + 1result = max(result, dp[i][j])return result一维dp
class Solution:def findLength(self, nums1: List[int], nums2: List[int]) -> int:dp = [0] * (len(nums2) + 1)result = 0# 遍历数组 nums1for i in range(1, len(nums1) + 1):# 倒序遍历数组 nums2for j in range(len(nums2), 0, -1):if nums1[i-1] == nums2[j-1]:dp[j] = dp[j-1] + 1result = max(dp[j], result)else:dp[j] = 0return result相关文章:

代码随想录 动态规划 13
300. 最长递增子序列 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子…...
lv6 嵌入式开发-Flappy bird项目
目录 1 项目功能总结 2 知识储备: 3 项目框图 4 Ncurses库介绍 做Flappy bird项目有什么用? 1. 复习、巩固c语言知识 2. 培养做项目的逻辑思维能力 3. 具备开发简单小游戏的能力 学会了Flappy bird项目,贪吃蛇和推房子两款小游戏也可…...

【Java】方法重写
概述 子类中出现了和父类一模一样的方法 当子类需要父类的功能,而功能主体中,子类有自己独特的内容,就可以通过重写父类中的方法,这样即延续了父类的功能,又定义了自己的特有内容 Override 是一个注解,可以…...

艺术表现形式
abstract expressionism 抽象表现主义 20世纪中期的一种艺术运动,包括多种风格和技巧,特别强调艺术家通过非传统和通常非具象的手段表达态度和情感的自由。 抽象表现主义用有力的笔触和滴落的颜料来表达情感和自发性。 简单地结合“abstract expression…...

PHP 反序列化漏洞:手写序列化文本
文章目录 参考环境序列化文本Scalar Type整数浮点数布尔值字符串 Compound Type数组数据结构序列化文本 对象数据结构序列化文本 Special TypeNULL数据结构序列化文本 手写序列化文本过程中的注意事项个数描述须于现实相符序列化文本前缀的大小写变化符号公共属性 参考 项目描…...
react.js在visual code 下的hello World
想学习reacr.js ,就开始做一个hello world。 我的环境是visual code ,所以我找这个环境下的例子。参照: https://code.visualstudio.com/docs/nodejs/reactjs-tutorial 要学习react.js ,还得先安装node.js,我在visual …...
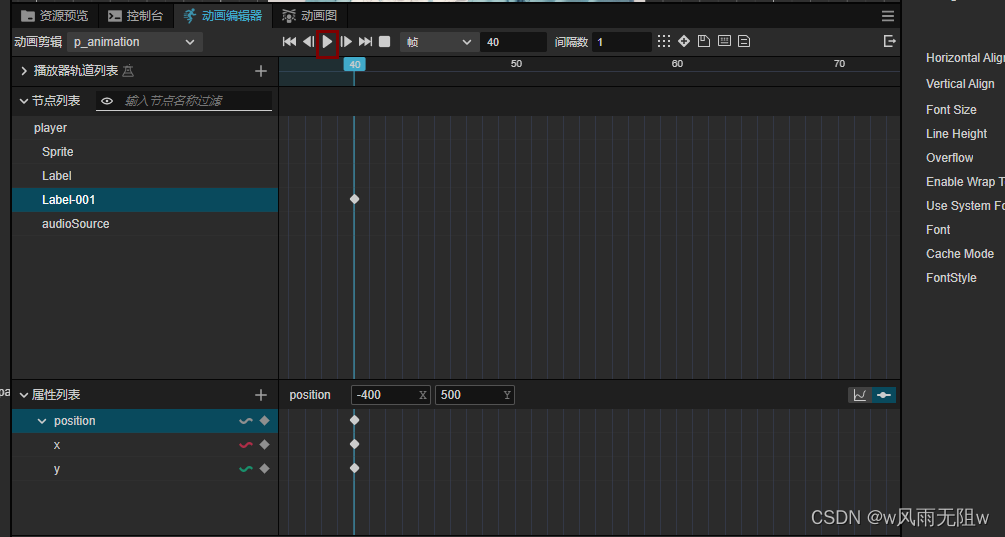
CocosCreator3.8研究笔记(二十四)CocosCreator 动画系统-动画编辑器实操-关键帧实现动态水印动画效果
上一篇,我们介绍了动画编辑器相关功能面板说明,感兴趣的朋友可以前往阅读: CocosCreator3.8研究笔记(二十三)CocosCreator 动画系统-动画编辑器相关功能面板说明。 熟悉了动画编辑器的基础操作,那么再使用动…...

第1篇 目标检测概述 —(3)YOLO系列算法
前言:Hello大家好,我是小哥谈。YOLO(You Only Look Once)系列算法是一种目标检测算法,主要用于实时物体检测。相较于传统的目标检测算法,YOLO具有更快的检测速度和更高的准确率。YOLO系列算法的核心思想是将…...

SpringBoot整合数据库连接
JDBC 1、SQL准备 DROP TABLE IF EXISTS t_book;CREATE TABLE t_book (book_id int(11) NOT NULL,book_name varchar(255) DEFAULT NULL,price int(11) DEFAULT NULL,stock int(11) DEFAULT NULL ) ENGINEInnoDB DEFAULT CHARSETutf8mb4;/*Data for the table t_book */insert…...

uni-app:canvas-绘制图形4(获取画布宽高,根据画布宽高进行图形绘制)
效果 代码 var width ; var height ; const query uni.createSelectorQuery(); //获取宽度 query.select(#firstCanvas).fields({ size: true }, (res) > { width res.width; height res.height; }).exec(); console.log(宽度width); console.log(高…...

EM@坐标@函数@图象的对称和翻折变换
文章目录 abstract翻折变换关于坐标轴翻折 f ( − x ) , f ( x ) f(-x),f(x) f(−x),f(x) − f ( x ) , f ( x ) -f(x),f(x) −f(x),f(x) 偶函数奇函数小结 其他翻折变换关于 y x y\pm x yx对称的直角坐标 关于 x u 对称 关于xu对称 关于xu对称的函数关于 y v yv yv对称的两…...

Python之json模块
JSON (JavaScript Object Notation),由 RFC 7159 (它取代了 RFC 4627) 和 ECMA-404 指定,是一个受 JavaScript 的对象字面值句法启发的轻量级数据交换格式。JSON独立于编程语言的文本格式来存储和表示数据,现在大部分的数据传输基本使用的都是…...
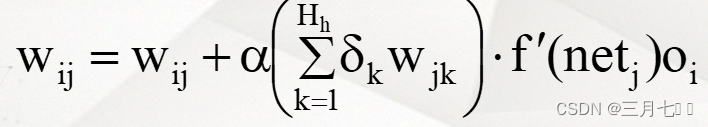
机器学习---BP算法
1. 多级网络 层号确定层的高低:层号较小者,层次较低,层号较大者,层次较高。 输入层:被记作第0层。该层负责接收来自网络外部的信息。 第j层:第j-1层的直接后继层(j>0)ÿ…...

继苹果、联发科后,传高通下一代5G芯片将由台积电以3纳米代工
台积电3纳米又有重量级客户加入。市场传出,继苹果、联发科之后,手机芯片大厂高通下一代5G旗舰芯片也将交由台积电以3纳米生产,最快将于10月下旬发表,成为台积电3纳米第三家客户。 针对相关传闻,至昨日(25日…...
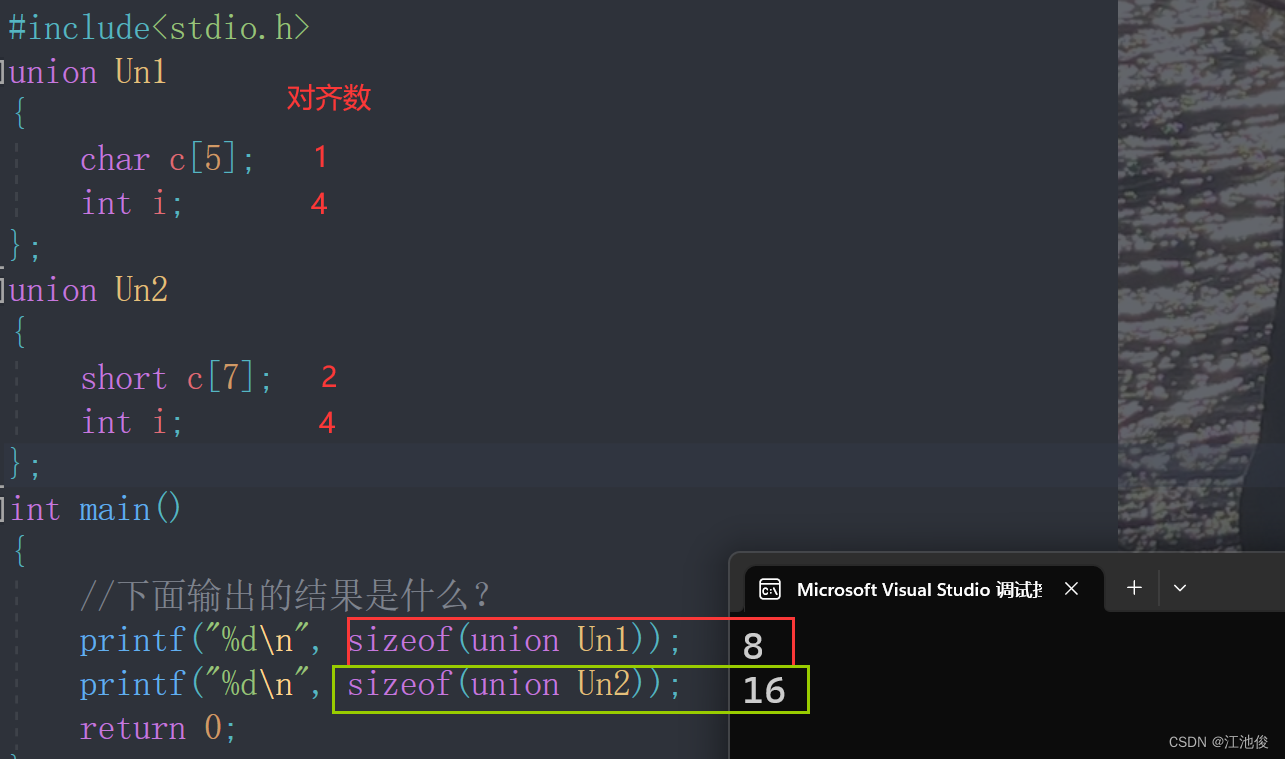
【自定义类型】--- 位段、枚举、联合
💓博客主页:江池俊的博客⏩收录专栏:C语言进阶之路👉专栏推荐:✅C语言初阶之路 ✅数据结构探索💻代码仓库:江池俊的代码仓库🎉欢迎大家点赞👍评论📝收藏⭐ 文…...
区块链(9):java区块链项目的Web服务实现之实现web服务
1 引入pom依赖 <dependency><groupId>org.eclipse.jetty</groupId><artifactId>jetty-server</artifactId><version>9.4.8.v20171121</version></dependency><dependency><groupId>org.eclipse.jetty</groupId…...

【CV】各种库安装报错及解决办法
目录 1.Error:Cannot unpack file… 1.Error:Cannot unpack file… 使用命令pip install -i https://pypi.tuna.tsinghua.edu.cn/simple --trusted-host pypi.tuna.tsinghua.edu.cn 包名安装 参考:解决Python使用pip安装库文件出现“Error&a…...
【算法系列篇】哈希表
文章目录 前言1. 两数之和1.1 题目要求1.2 做题思路1.3 Java代码实现 2. 判断是否为字符重排2.1 题目要求2.2 做题思路2.3 Java代码实现 3. 存在重复元素3.1 题目要求3.2 做题思路3.3 Java代码实现 4. 存在重复元素II4.2 题目要求4.2 做题思路4.3 Java代码实现 5. 字母异位词分…...
计算机视觉——飞桨深度学习实战-起始篇
后面我会直接跳到实战项目,将计算机视觉的主要任务和目标都实现一遍,但是需要大家下去自己多理解和学习一下。例如,什么是深度学习,什么是计算机视觉,什么是自然语言处理,计算机视觉的主要任务有哪些&#…...

vscode中运行脚手架项目报表
必选在cmd页面里面安装脚手架离谱啊,不然无法执行npm命令啊 vscode运行vue项目_小何不秃头06的博客-CSDN博客 finereport激活成功 - 帆软 (fanruan.com)...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
