深度学习入门(六十七)循环神经网络——注意力机制
深度学习入门(六十七)循环神经网络——注意力机制
- 前言
- 循环神经网络——注意力机制
- 课件
- 心理学
- 注意力机制
- 注意力机制是显式地考虑随意线索
- 非参注意力池化层
- Nadaraya-Watson 核回归:
- 总结
- 教材(注意力提示)
- 1 生物学中的注意力提示
- 2 查询、键和值
- 3 注意力的可视化
- 4 小结
- 教材(注意力汇聚:Nadaraya-Watson 核回归)
- 1 生成数据集
- 2 平均汇聚
- 3 非参数注意力汇聚
- 4 带参数注意力汇聚
- 4.1 批量矩阵乘法
- 4.2 定义模型
- 4.3 训练
- 5 小结
前言
核心内容来自博客链接1博客连接2希望大家多多支持作者
本文记录用,防止遗忘
循环神经网络——注意力机制
课件
心理学
- 动物需要在复杂环境下有效关注值得注意的点
- 心理学框架:人类根据随意线索和不随意线索选择注意点
注意力机制
卷积、全连接、池化层都只考虑不随意线索(没有明确的目标)
池化操作通常是将感受野范围中的最大值提取出来(最大池化)
卷积操作通常是对输入全部通过卷积核进行操作,然后提取出一些比较明显的特征
注意力机制是显式地考虑随意线索
随意线索被称之为查询(query)---- 所想要做的事情
每个输入是一个值(value)和不随意线索(key)的对 ---- 可以理解为环境,就是一些键值对,key 和 value 可以相同,也可以不同
通过注意力池化层来有偏向性地选择某些输入 ---- 根据 query 有偏向地选择输入,跟之前的池化层有所不同,这里显式地加入了 query,然后根据 query 查询所需要的东西
非参注意力池化层

非参:不需要学习参数
x – key
y – value
f(x)-- 对应所要查询的东西
(x,y) – key-value对(候选)
平均池化:之所以是最简单的方案,是因为不需要管所查询的东西(也就是f(x)中的 x ),而只需要无脑地对 y 求和取平均就可以了
Nadaraya-Watson 核回归:
核:K 函数,它可以认为是衡量 x 和 xi 之间距离的函数
数据就是给定的数据,对于新给定的值来讲,只需要在给定的数据中进行查询就可以了(选择和新给定的值比较相近的数据,然后将这些数据对应的 value 值然后进行加权求和,从而得到最终的 query),所以不需要学习参数
K 的选择:高斯核
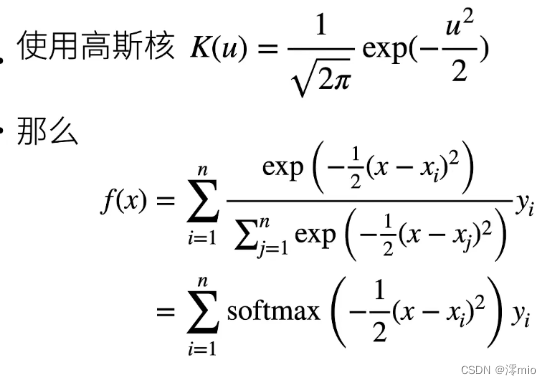
u:代表 x 和 xi 之间的距离
exp:作用是将最终的结果变成大于 0 的数
softmax:得到 0 到 1 之间的数作为权重
在上式的基础上添加一个可以学习的 w :
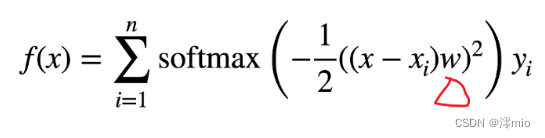
总结
1、心理学认为人通过随意线索和不随意线索选择注意点
2、注意力机制中,通过query(随意线索)和 key(不随意线索)来有偏向性地选择输入,一般可以写作
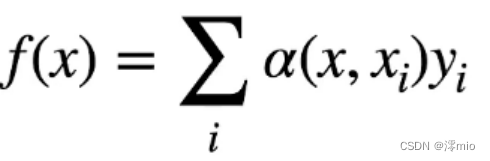
f(x)的 key 和所有的不随意线索的 key 做距离上的计算(α(x,xi),通常称为注意力权重),分别作为所有的 value 的权重
这并不是一个新兴的概念,早在 60 年代就已经有非参数的注意力机制了
教材(注意力提示)
自经济学研究稀缺资源分配以来,人们正处在“注意力经济”时代, 即人类的注意力被视为可以交换的、有限的、有价值的且稀缺的商品。 许多商业模式也被开发出来去利用这一点: 在音乐或视频流媒体服务上,人们要么消耗注意力在广告上,要么付钱来隐藏广告; 为了在网络游戏世界的成长,人们要么消耗注意力在游戏战斗中, 从而帮助吸引新的玩家,要么付钱立即变得强大。 总之,注意力不是免费的。
注意力是稀缺的,而环境中的干扰注意力的信息却并不少。 比如人类的视觉神经系统大约每秒收到10810^8108位的信息, 这远远超过了大脑能够完全处理的水平。 幸运的是,人类的祖先已经从经验(也称为数据)中认识到 “并非感官的所有输入都是一样的”。 在整个人类历史中,这种只将注意力引向感兴趣的一小部分信息的能力, 使人类的大脑能够更明智地分配资源来生存、成长和社交, 例如发现天敌、找寻食物和伴侣。
1 生物学中的注意力提示
注意力是如何应用于视觉世界中的呢? 这要从当今十分普及的双组件(two-component)的框架开始讲起: 这个框架的出现可以追溯到19世纪90年代的威廉·詹姆斯, 他被认为是“美国心理学之父” 。 在这个框架中,受试者基于非自主性提示和自主性提示 有选择地引导注意力的焦点。
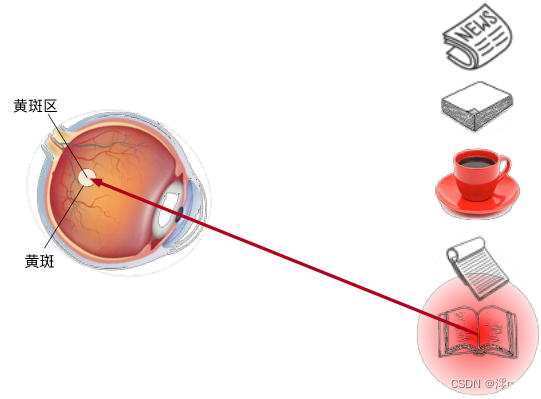
非自主性提示是基于环境中物体的突出性和易见性。 想象一下,假如我们面前有五个物品: 一份报纸、一篇研究论文、一杯咖啡、一本笔记本和一本书, 就像下图。 所有纸制品都是黑白印刷的,但咖啡杯是红色的。 换句话说,这个咖啡杯在这种视觉环境中是突出和显眼的, 不由自主地引起人们的注意。 所以我们会把视力最敏锐的地方放到咖啡上, 如图所示。
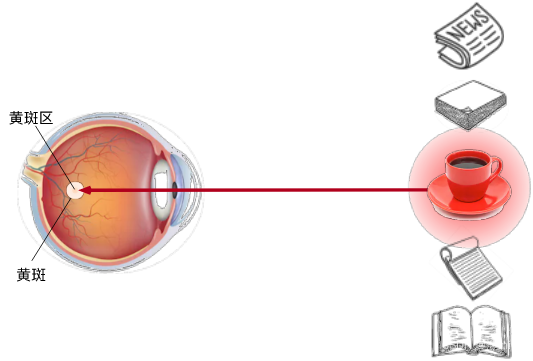
喝咖啡后,我们会变得兴奋并想读书, 所以转过头,重新聚焦眼睛,然后看看书, 就像下图中描述那样。 与上图中由于突出性导致的选择不同, 此时选择书是受到了认知和意识的控制, 因此注意力在基于自主性提示去辅助选择时将更为谨慎。 受试者的主观意愿推动,选择的力量也就更强大。
2 查询、键和值
自主性的与非自主性的注意力提示解释了人类的注意力的方式, 下面来看看如何通过这两种注意力提示, 用神经网络来设计注意力机制的框架,
首先,考虑一个相对简单的状况, 即只使用非自主性提示。 要想将选择偏向于感官输入, 则可以简单地使用参数化的全连接层, 甚至是非参数化的最大汇聚层或平均汇聚层。
因此,“是否包含自主性提示”将注意力机制与全连接层或汇聚层区别开来。 在注意力机制的背景下,自主性提示被称为查询(query)。 给定任何查询,注意力机制通过注意力汇聚(attention pooling) 将选择引导至感官输入(sensory inputs,例如中间特征表示)。 在注意力机制中,这些感官输入被称为值(value)。 更通俗的解释,每个值都与一个键(key)配对, 这可以想象为感官输入的非自主提示。 如图所示,可以通过设计注意力汇聚的方式, 便于给定的查询(自主性提示)与键(非自主性提示)进行匹配, 这将引导得出最匹配的值(感官输入)。
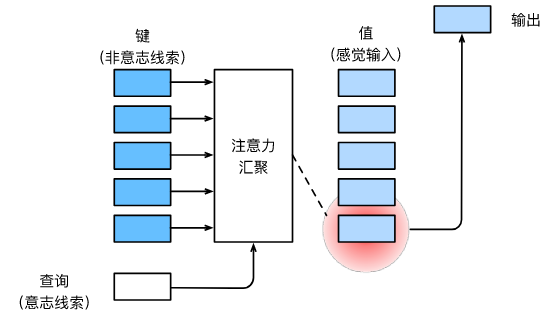
鉴于上面所提框架在图中的主导地位, 因此这个框架下的模型将成为本章的中心。 然而,注意力机制的设计有许多替代方案。 例如可以设计一个不可微的注意力模型, 该模型可以使用强化学习方法 (Mnih et al., 2014)进行训练。
3 注意力的可视化
平均汇聚层可以被视为输入的加权平均值, 其中各输入的权重是一样的。 实际上,注意力汇聚得到的是加权平均的总和值, 其中权重是在给定的查询和不同的键之间计算得出的。
import torch
from d2l import torch as d2l
为了可视化注意力权重,需要定义一个show_heatmaps函数。 其输入matrices的形状是 (要显示的行数,要显示的列数,查询的数目,键的数目)。
#@save
def show_heatmaps(matrices, xlabel, ylabel, titles=None, figsize=(2.5, 2.5),cmap='Reds'):"""显示矩阵热图"""d2l.use_svg_display()num_rows, num_cols = matrices.shape[0], matrices.shape[1]fig, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize,sharex=True, sharey=True, squeeze=False)for i, (row_axes, row_matrices) in enumerate(zip(axes, matrices)):for j, (ax, matrix) in enumerate(zip(row_axes, row_matrices)):pcm = ax.imshow(matrix.detach().numpy(), cmap=cmap)if i == num_rows - 1:ax.set_xlabel(xlabel)if j == 0:ax.set_ylabel(ylabel)if titles:ax.set_title(titles[j])fig.colorbar(pcm, ax=axes, shrink=0.6);
下面使用一个简单的例子进行演示。 在本例子中,仅当查询和键相同时,注意力权重为1,否则为0。
attention_weights = torch.eye(10).reshape((1, 1, 10, 10))
show_heatmaps(attention_weights, xlabel='Keys', ylabel='Queries')
输出:
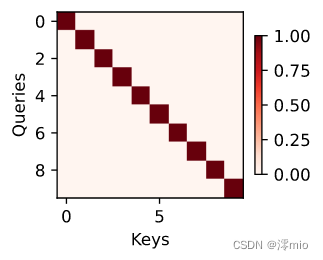
后面的章节内容将经常调用show_heatmaps函数来显示注意力权重。
4 小结
-
人类的注意力是有限的、有价值和稀缺的资源。
-
受试者使用非自主性和自主性提示有选择性地引导注意力。前者基于突出性,后者则依赖于意识。
-
注意力机制与全连接层或者汇聚层的区别源于增加的自主提示。
-
由于包含了自主性提示,注意力机制与全连接的层或汇聚层不同。
-
注意力机制通过注意力汇聚使选择偏向于值(感官输入),其中包含查询(自主性提示)和键(非自主性提示)。键和值是成对的。
-
可视化查询和键之间的注意力权重是可行的。
教材(注意力汇聚:Nadaraya-Watson 核回归)
上部分介绍了框架下的注意力机制的主要成分: 查询(自主提示)和键(非自主提示)之间的交互形成了注意力汇聚; 注意力汇聚有选择地聚合了值(感官输入)以生成最终的输出。 本节将介绍注意力汇聚的更多细节, 以便从宏观上了解注意力机制在实践中的运作方式。 具体来说,1964年提出的Nadaraya-Watson核回归模型 是一个简单但完整的例子,可以用于演示具有注意力机制的机器学习。
import torch
from torch import nn
from d2l import torch as d2l
1 生成数据集
n_train = 50 # 训练样本数
x_train, _ = torch.sort(torch.rand(n_train) * 5) # 排序后的训练样本def f(x):return 2 * torch.sin(x) + x**0.8y_train = f(x_train) + torch.normal(0.0, 0.5, (n_train,)) # 训练样本的输出
x_test = torch.arange(0, 5, 0.1) # 测试样本
y_truth = f(x_test) # 测试样本的真实输出
n_test = len(x_test) # 测试样本数
n_test
输出
50
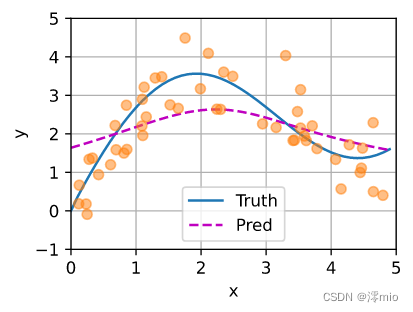
下面的函数将绘制所有的训练样本(样本由圆圈表示), 不带噪声项的真实数据生成函数fff(标记为“Truth”), 以及学习得到的预测函数(标记为“Pred”)。
def plot_kernel_reg(y_hat):d2l.plot(x_test, [y_truth, y_hat], 'x', 'y', legend=['Truth', 'Pred'],xlim=[0, 5], ylim=[-1, 5])d2l.plt.plot(x_train, y_train, 'o', alpha=0.5);
2 平均汇聚
先使用最简单的估计器来解决回归问题。 基于平均汇聚来计算所有训练样本输出值的平均值:
f(x)=1n∑i=1nyi,f(x) = \frac{1}{n}\sum_{i=1}^n y_i,f(x)=n1i=1∑nyi,
如下图所示,这个估计器确实不够聪明。 真实函数fff(“Truth”)和预测函数(“Pred”)相差很大。
y_hat = torch.repeat_interleave(y_train.mean(), n_test)
plot_kernel_reg(y_hat)
输出:
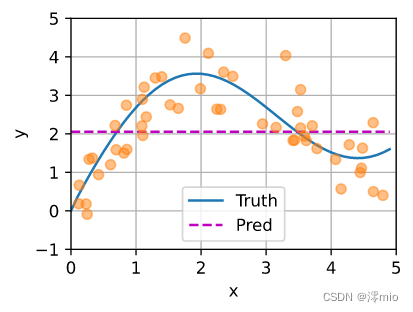
3 非参数注意力汇聚
显然,平均汇聚忽略了输入xix_ixi。 于是Nadaraya和 Watson提出了一个更好的想法, 根据输入的位置对输出yiy_iyi进行加权:
f(x)=∑i=1nK(x−xi)∑j=1nK(x−xj)yi(10.2.3)f(x) = \sum_{i=1}^n \frac{K(x - x_i)}{\sum_{j=1}^n K(x - x_j)} y_i \qquad(10.2.3)f(x)=i=1∑n∑j=1nK(x−xj)K(x−xi)yi(10.2.3)
其中KKK是核(kernel)。 公式 (10.2.3)所描述的估计器被称为 Nadaraya-Watson核回归(Nadaraya-Watson kernel regression)。 这里不会深入讨论核函数的细节, 但受此启发, 我们可以从注意力机制框架的角度重写 (10.2.3), 成为一个更加通用的注意力汇聚(attention pooling)公式:
f(x)=∑i=1nα(x,xi)yi(10.2.4)f(x) = \sum_{i=1}^n \alpha(x, x_i) y_i \qquad(10.2.4)f(x)=i=1∑nα(x,xi)yi(10.2.4)
其中xxx是查询,(xi,yi)(x_i, y_i)(xi,yi)是键值对。 比较 (10.2.4)和 (10.2.2), 注意力汇聚是yiy_iyi的加权平均。 将查询xxx和键xix_ixi之间的关系建模为 注意力权重(attention weight), 如 (10.2.4)所示, 这个权重将被分配给每一个对应值yiy_iyi。 对于任何查询,模型在所有键值对注意力权重都是一个有效的概率分布: 它们是非负的,并且总和为1。
为了更好地理解注意力汇聚, 下面考虑一个高斯核(Gaussian kernel),其定义为:
K(u)=12πexp(−u22)(10.2.5)K(u) = \frac{1}{\sqrt{2\pi}} \exp(-\frac{u^2}{2})\qquad (10.2.5)K(u)=2π1exp(−2u2)(10.2.5)
将高斯核代入 (10.2.4)和 (10.2.3)可以得到:
f(x)=∑i=1nα(x,xi)yi=∑i=1nexp(−12(x−xi)2)∑j=1nexp(−12(x−xj)2)yi=∑i=1nsoftmax(−12(x−xi)2)yi.(10.2.6)\begin{split}\begin{aligned} f(x) &=\sum_{i=1}^n \alpha(x, x_i) y_i\\ &= \sum_{i=1}^n \frac{\exp\left(-\frac{1}{2}(x - x_i)^2\right)}{\sum_{j=1}^n \exp\left(-\frac{1}{2}(x - x_j)^2\right)} y_i \\&= \sum_{i=1}^n \mathrm{softmax}\left(-\frac{1}{2}(x - x_i)^2\right) y_i. \end{aligned}\end{split} \qquad (10.2.6)f(x)=i=1∑nα(x,xi)yi=i=1∑n∑j=1nexp(−21(x−xj)2)exp(−21(x−xi)2)yi=i=1∑nsoftmax(−21(x−xi)2)yi.(10.2.6)
在 (10.2.6)中, 如果一个键xix_ixi越是接近给定的查询xxx, 那么分配给这个键对应值yiy_iyi的注意力权重就会越大, 也就“获得了更多的注意力”。
值得注意的是,Nadaraya-Watson核回归是一个非参数模型。 因此, (10.2.6)是 非参数的注意力汇聚(nonparametric attention pooling)模型。 接下来,我们将基于这个非参数的注意力汇聚模型来绘制预测结果。 从绘制的结果会发现新的模型预测线是平滑的,并且比平均汇聚的预测更接近真实。
# X_repeat的形状:(n_test,n_train),
# 每一行都包含着相同的测试输入(例如:同样的查询)
X_repeat = x_test.repeat_interleave(n_train).reshape((-1, n_train))
# x_train包含着键。attention_weights的形状:(n_test,n_train),
# 每一行都包含着要在给定的每个查询的值(y_train)之间分配的注意力权重
attention_weights = nn.functional.softmax(-(X_repeat - x_train)**2 / 2, dim=1)
# y_hat的每个元素都是值的加权平均值,其中的权重是注意力权重
y_hat = torch.matmul(attention_weights, y_train)
plot_kernel_reg(y_hat)
输出:
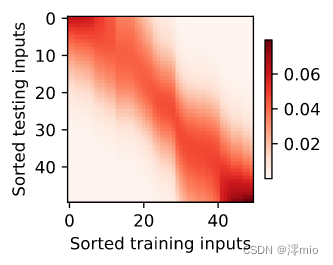
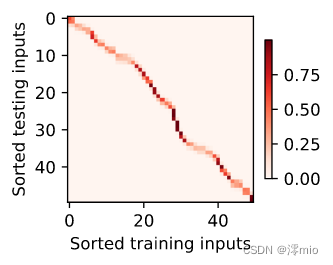
现在来观察注意力的权重。 这里测试数据的输入相当于查询,而训练数据的输入相当于键。 因为两个输入都是经过排序的,因此由观察可知“查询-键”对越接近, 注意力汇聚的注意力权重就越高。
d2l.show_heatmaps(attention_weights.unsqueeze(0).unsqueeze(0),xlabel='Sorted training inputs',ylabel='Sorted testing inputs')
输出
4 带参数注意力汇聚
非参数的Nadaraya-Watson核回归具有一致性(consistency)的优点: 如果有足够的数据,此模型会收敛到最优结果。 尽管如此,我们还是可以轻松地将可学习的参数集成到注意力汇聚中。
例如,与 (10.2.6)略有不同, 在下面的查询xxx和键xix_ixi之间的距离乘以可学习参数www:
f(x)=∑i=1nα(x,xi)yi=∑i=1nexp(−12((x−xi)w)2)∑j=1nexp(−12((x−xj)w)2)yi=∑i=1nsoftmax(−12((x−xi)w)2)yi.(10.2.7)\begin{split}\begin{aligned}f(x) &= \sum_{i=1}^n \alpha(x, x_i) y_i \\&= \sum_{i=1}^n \frac{\exp\left(-\frac{1}{2}((x - x_i)w)^2\right)}{\sum_{j=1}^n \exp\left(-\frac{1}{2}((x - x_j)w)^2\right)} y_i \\&= \sum_{i=1}^n \mathrm{softmax}\left(-\frac{1}{2}((x - x_i)w)^2\right) y_i.\end{aligned}\end{split} \qquad (10.2.7)f(x)=i=1∑nα(x,xi)yi=i=1∑n∑j=1nexp(−21((x−xj)w)2)exp(−21((x−xi)w)2)yi=i=1∑nsoftmax(−21((x−xi)w)2)yi.(10.2.7)
本节的余下部分将通过训练这个模型 (10.2.7)来学习注意力汇聚的参数。
4.1 批量矩阵乘法
为了更有效地计算小批量数据的注意力, 我们可以利用深度学习开发框架中提供的批量矩阵乘法。
假设第一个小批量数据包含nnn个矩阵X1,…,Xn\mathbf{X}_1,\ldots, \mathbf{X}_nX1,…,Xn, 形状为a×ba\times ba×b, 第二个小批量包含nnn个矩阵Y1,…,Yn\mathbf{Y}_1, \ldots, \mathbf{Y}_nY1,…,Yn, 形状为b×cb\times cb×c。 它们的批量矩阵乘法得到nnn个矩阵X1Y1,…,XnYn\mathbf{X}_1\mathbf{Y}_1, \ldots, \mathbf{X}_n\mathbf{Y}_nX1Y1,…,XnYn , 形状为a×ca\times ca×c。 因此,假定两个张量的形状分别是(n,a,b)(n,a,b)(n,a,b)和(n,b,c)(n,b,c)(n,b,c), 它们的批量矩阵乘法输出的形状为(n,a,c)(n,a,c)(n,a,c)。
X = torch.ones((2, 1, 4))
Y = torch.ones((2, 4, 6))
torch.bmm(X, Y).shape
输出
torch.Size([2, 1, 6])
在注意力机制的背景中,我们可以使用小批量矩阵乘法来计算小批量数据中的加权平均值。
weights = torch.ones((2, 10)) * 0.1
values = torch.arange(20.0).reshape((2, 10))
torch.bmm(weights.unsqueeze(1), values.unsqueeze(-1))
输出
tensor([[[ 4.5000]],[[14.5000]]])
4.2 定义模型
基于 (10.2.7)中的 带参数的注意力汇聚,使用小批量矩阵乘法, 定义Nadaraya-Watson核回归的带参数版本为:
class NWKernelRegression(nn.Module):def __init__(self, **kwargs):super().__init__(**kwargs)self.w = nn.Parameter(torch.rand((1,), requires_grad=True))def forward(self, queries, keys, values):# queries和attention_weights的形状为(查询个数,“键-值”对个数)queries = queries.repeat_interleave(keys.shape[1]).reshape((-1, keys.shape[1]))self.attention_weights = nn.functional.softmax(-((queries - keys) * self.w)**2 / 2, dim=1)# values的形状为(查询个数,“键-值”对个数)return torch.bmm(self.attention_weights.unsqueeze(1),values.unsqueeze(-1)).reshape(-1)
4.3 训练
接下来,将训练数据集变换为键和值用于训练注意力模型。 在带参数的注意力汇聚模型中, 任何一个训练样本的输入都会和除自己以外的所有训练样本的“键-值”对进行计算, 从而得到其对应的预测输出。
# X_tile的形状:(n_train,n_train),每一行都包含着相同的训练输入
X_tile = x_train.repeat((n_train, 1))
# Y_tile的形状:(n_train,n_train),每一行都包含着相同的训练输出
Y_tile = y_train.repeat((n_train, 1))
# keys的形状:('n_train','n_train'-1)
keys = X_tile[(1 - torch.eye(n_train)).type(torch.bool)].reshape((n_train, -1))
# values的形状:('n_train','n_train'-1)
values = Y_tile[(1 - torch.eye(n_train)).type(torch.bool)].reshape((n_train, -1))
训练带参数的注意力汇聚模型时,使用平方损失函数和随机梯度下降。
net = NWKernelRegression()
loss = nn.MSELoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=0.5)
animator = d2l.Animator(xlabel='epoch', ylabel='loss', xlim=[1, 5])for epoch in range(5):trainer.zero_grad()l = loss(net(x_train, keys, values), y_train)l.sum().backward()trainer.step()print(f'epoch {epoch + 1}, loss {float(l.sum()):.6f}')animator.add(epoch + 1, float(l.sum()))
输出:
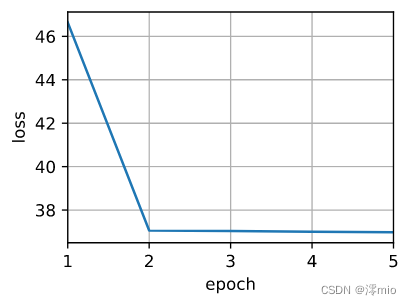
如下所示,训练完带参数的注意力汇聚模型后可以发现: 在尝试拟合带噪声的训练数据时, 预测结果绘制的线不如之前非参数模型的平滑。
# keys的形状:(n_test,n_train),每一行包含着相同的训练输入(例如,相同的键)
keys = x_train.repeat((n_test, 1))
# value的形状:(n_test,n_train)
values = y_train.repeat((n_test, 1))
y_hat = net(x_test, keys, values).unsqueeze(1).detach()
plot_kernel_reg(y_hat)
输出
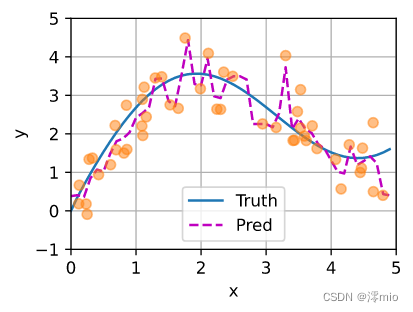
为什么新的模型更不平滑了呢? 下面看一下输出结果的绘制图: 与非参数的注意力汇聚模型相比, 带参数的模型加入可学习的参数后, 曲线在注意力权重较大的区域变得更不平滑。
d2l.show_heatmaps(net.attention_weights.unsqueeze(0).unsqueeze(0),xlabel='Sorted training inputs',ylabel='Sorted testing inputs')
输出
5 小结
-
Nadaraya-Watson核回归是具有注意力机制的机器学习范例。
-
Nadaraya-Watson核回归的注意力汇聚是对训练数据中输出的加权平均。从注意力的角度来看,分配给每个值的注意力权重取决于将值所对应的键和查询作为输入的函数。
-
注意力汇聚可以分为非参数型和带参数型。
相关文章:

深度学习入门(六十七)循环神经网络——注意力机制
深度学习入门(六十七)循环神经网络——注意力机制前言循环神经网络——注意力机制课件心理学注意力机制注意力机制是显式地考虑随意线索非参注意力池化层Nadaraya-Watson 核回归:总结教材(注意力提示)1 生物学中的注意…...
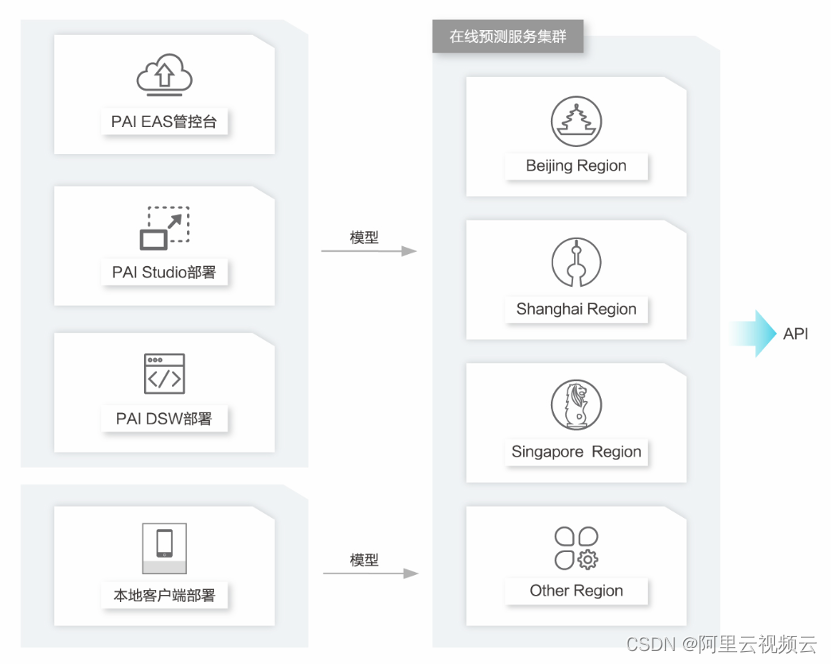
阿里云云通信风控系统的架构与实践
作者:铭杰 阿里云云通信创立于 2017 年,历经 5 年发展已经孵化出智能消息、智能语音、隐私号、号码百科等多个热门产品。目前,已成为了国内云通信市场的领头羊,在国际市场上服务范围也覆盖了 200 多个国家。随着业务的不断壮大&am…...

【性能测试】loadrunner(一)知识准备
【性能测试】loadrunner(一)知识准备 目录:导读 1.0. 前言 1.1 性能测试术语介绍 1.2 性能测试分类 1.3 HTTP我们需要知道的 1.4 Loadrunner 12.55安装 1.0. 前言 在性能测试中,牵扯到了许多比较杂的知识点,…...
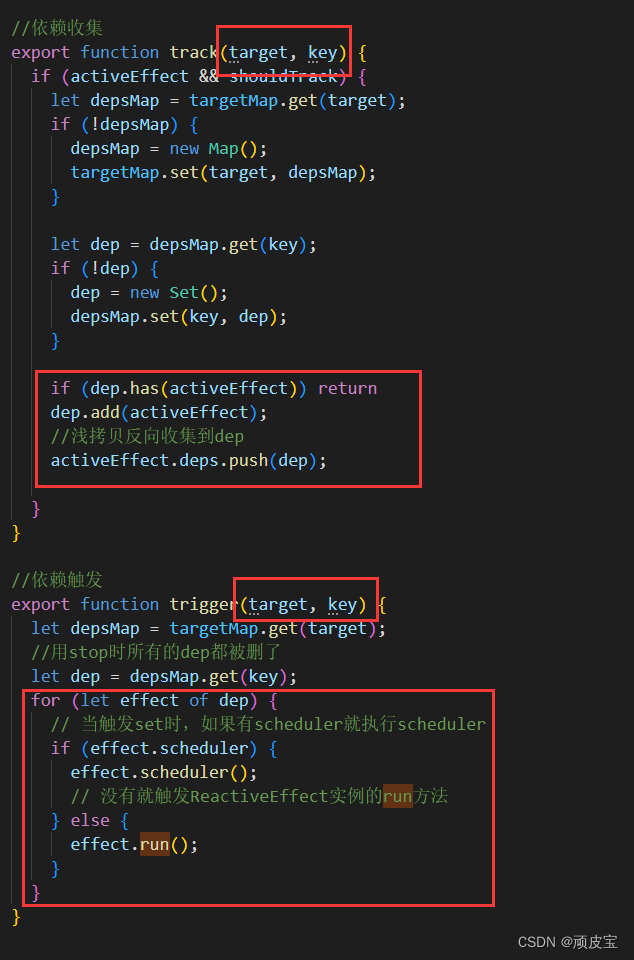
【Vue3源码】第五章 ref的原理 实现ref
【Vue3源码】第五章 ref的原理 实现ref 上一章节我们实现了reactive 和 readonly 嵌套对象转换功能,以及shallowReadonly 和isProxy几个简单的API。 这一章我们开始实现 ref 及其它配套的isRef、unRef 和 proxyRefs 1、实现ref 接受一个内部值,返回一…...
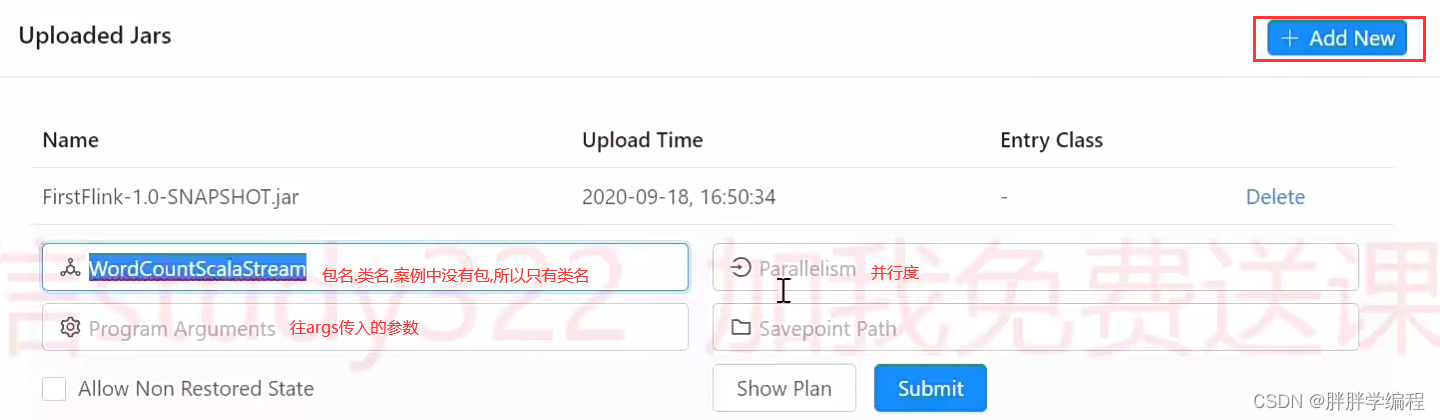
[Flink]部署模式(看pdf上的放上面)
运行一个wordcountval dataStream: DataStream[String] environment.socketTextStream("hadoop1", 7777) //流式数据不能进行groupBy,流式数据要来一条处理一次.0表示第一个元素,1表示第二个元素 //keyBy(0)根据第一个元素进行分组 val out: DataStream[(String, In…...

Linux 查看 CPU 信息,机器型号,内存等信息
平时用的可能少,但需要记住,使用的命令,转载https://my.oschina.net/hunterli/blog/140783,以记录学习 系统 # uname -a # 查看内核/操作系统/CPU信息 # head -n 1 /etc/issue # 查看操作系统版本 # cat /proc/…...
)
三维量子力学 量子力学(3)
动量ppp有三个分量,为pxp_xpx等。它们分别满足与位置坐标的对易关系,比如px−iℏ∂∂xp_x-i\hbar\frac{\partial }{\partial x}px−iℏ∂x∂。可以用位置坐标梯度算符表示即p−iℏ∇\bm{p}-i\hbar\nablap−iℏ∇。位置矢量用r\bm{r}r表示。 在d3r…...

Blazor入门100天 : 身份验证和授权 (6) - 使用 FreeSql orm 管理ids数据
目录 建立默认带身份验证 Blazor 程序角色/组件/特性/过程逻辑DB 改 Sqlite将自定义字段添加到用户表脚手架拉取IDS文件,本地化资源freesql 生成实体类,freesql 管理ids数据表初始化 Roles,freesql 外键 > 导航属性完善 freesql 和 bb 特性 本节源码 https://github.com/…...

Java文件IO操作:File类的相关内容
Java文件IO操作一、File类1.相对路径和绝对路径2.路径分隔符(同一路径下、多个路径下)3.实例化4.常见方法一、File类 File类继承自Object类,实现了Serializable接口和Comparable接口; File类属于java.io包; File类是文…...
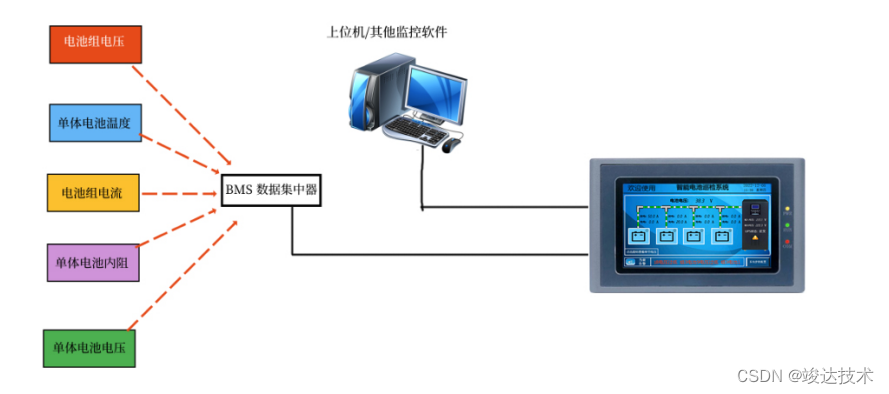
竣达技术 | 巡检触摸屏配合电池柜,电池安全放首位!
机房蓄电池常见的故障 1.机房电池着火和爆炸 目前在数据机房蓄电池爆炸着火事故频发,导致业主损失严重。一般机房电池是由于其中一节电池裂化后未妥善管理,电池急剧恶化导致爆炸着火。由于电池是串联及并联在使用,只要一节着火燃烧整片瞬间…...

什么是自动化运维?为什么选择Python做自动化运维?
“Python自动化运维”这个词,想必大家都听说过,但是很多人对它并不了解,也不知道是做什么的,那么你对Python自动化运维了解多少呢?跟着蛋糕往下看。 什么是Python自动化运维? 随着技术的进步、业务需求的快速增长,…...

【经验】移植环境requirement时报错
问题描述 在使用pip freeze > ./requirements.txt和pip install -r requirement.txt (requirements.txt文件用来记录当前程序的所有依赖包及其精确版本号)从一台电脑移植到另一台电脑的 conda 环境时,出现了一堆类似的报错: E…...

计算机专业要考什么证书?
大家好,我是良许。 从去年 12 月开始,我已经在视频号、抖音等主流视频平台上连续更新视频到现在,并得到了不错的评价。 视频 100% 原创录制,绝非垃圾搬运号,每个视频都花了很多时间精力用心制作,欢迎大家…...

一个列表引发的思考(简单版)
最近老板让我按照设计图写一个页面,不嫌丢人的说这是我第一次写页面,哈哈哈。 然后设计图里有一个这样的需求,感觉挺有意思的。 为什么感觉有意思呢,因为这个列表它前面是图片,然后单行和双行的不一样。(请…...
Unity C#中的序列化与反序列化)
Protobuf 学习简记(三)Unity C#中的序列化与反序列化
Protobuf 学习简记(三)Unity C#中的序列化与反序列化对文本的序列化与反序列化内存二进制流的序列化与反序列化方法一方法二参考链接对文本的序列化与反序列化 private void Text() {TestMsg1 myTestMsg new TestMsg1();myTestMsg.TestInt32 1;myTest…...

Flask入门(10):Flask使用SQLAlchemy
目录11.SQLAlchemy11.1 简介11.2 安装11.3 基本使用11.4 连接11.5 数据类型11.6 执行原生sql11.7 插入数据11. 8 删改操作11.9 查询11.SQLAlchemy 11.1 简介 SQLAlchemy的是Python的SQL工具包和对象关系映射,给应用程序开发者提供SQL的强大功能和灵活性。它提供了…...

我的 System Verilog 学习记录(4)
引言 本文简单介绍 System Verilog 语言的 数据类型。 前文链接: 我的 System Verilog 学习记录(1) 我的 System Verilog 学习记录(2) 我的 System Verilog 学习记录(3) 数据类型简介 Sys…...

Git : 本地分支与远程分支的映射关系
概述 本文介绍 git 环境中本地分支与远程分支的映射关系的查看和调整。 1、查看本地分支与远程分支的映射关系 执行如下命令: git branch -vv注意就是两个 v ,没有写错。 可以获得分支映射结果: dev fa***** [github/dev] update * main…...
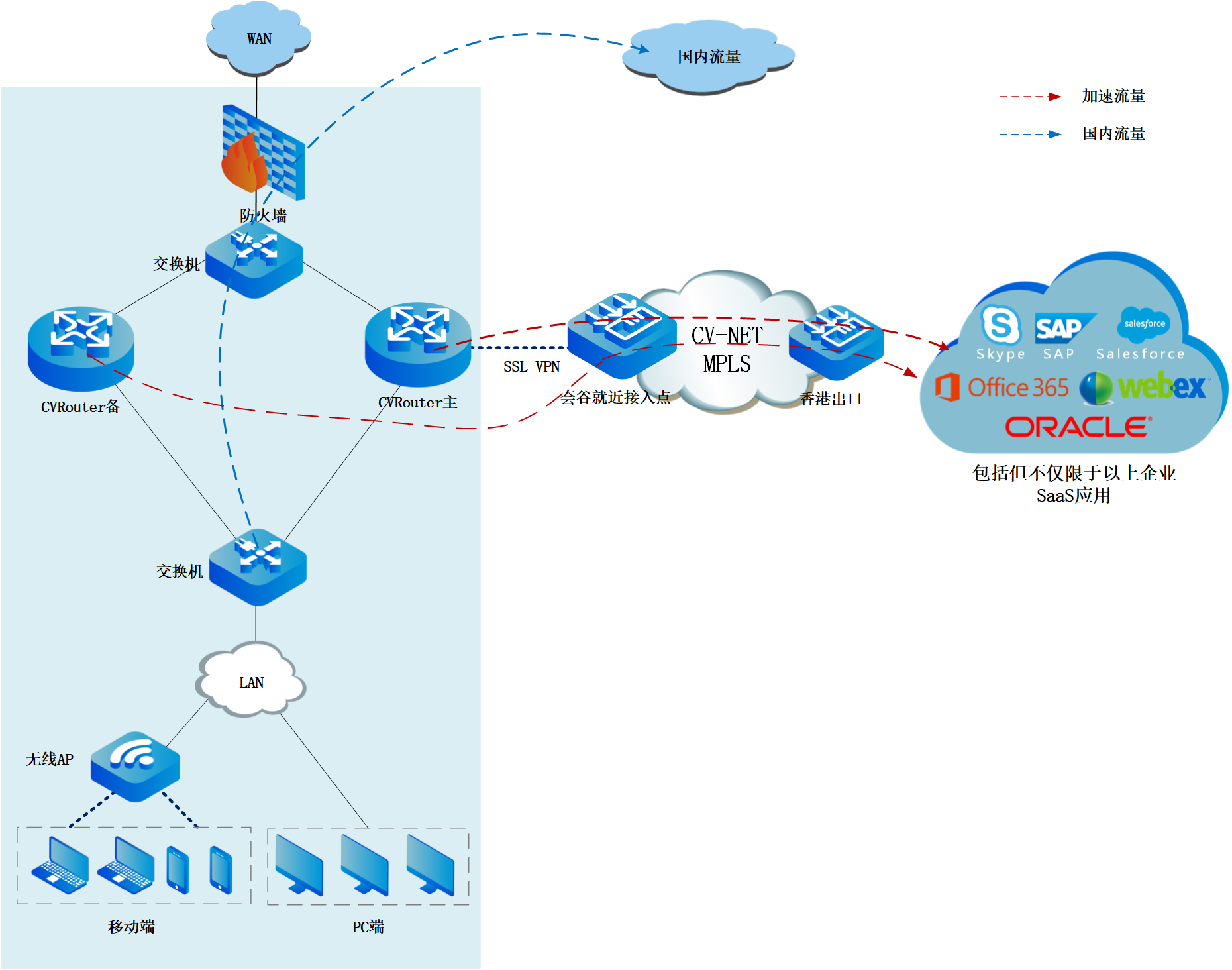
运维必看|跨国公司几千员工稳定访问Office365,怎么实现?
【客户背景】本次分享的客户是全球传感器领域的领导者,其核心产品为电流和电压传感器,被广泛应用于驱动和焊接、可再利用能源以及电源、牵引、高精度、传统和新能源汽车等领域。 作为一家中等规模的全球化公司,该公司在北京、日本、西欧、东欧…...

Python GDAL读取栅格数据并基于质量评估波段QA对指定数据加以筛选掩膜
本文介绍基于Python语言中gdal模块,对遥感影像数据进行栅格读取与计算,同时基于QA波段对像元加以筛选、掩膜的操作。本文所要实现的需求具体为:现有自行计算的全球叶面积指数(LAI).tif格式栅格产品(下称“自…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...
