CF1692C Where‘s the Bishop? 题解
CF1692C Where's the Bishop? 题解
- 题目
- 链接
- 字面描述
- 题面翻译
- 题目描述
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 代码实现
题目
链接
https://www.luogu.com.cn/problem/CF1692C
字面描述
题面翻译
题目描述
有一个8×88\times88×8的棋盘,列编号从左到右递增,行编号从上到下递增。
给出一个棋盘,上面用KaTeX parse error: Expected 'EOF', got '#' at position 1: #̲标明了主教的攻击范围。请你找出主教的位置坐标,并输出其行、列编号。
保证:主教的行、列编号均在222与777之间。
你需要回答ttt组测试数据。 (1≤t≤36)(1\le t \le 36)(1≤t≤36)
题目描述
Mihai has an $ 8 \times 8 $ chessboard whose rows are numbered from $ 1 $ to $ 8 $ from top to bottom and whose columns are numbered from $ 1 $ to $ 8 $ from left to right.
Mihai has placed exactly one bishop on the chessboard. The bishop is not placed on the edges of the board. (In other words, the row and column of the bishop are between $ 2 $ and $ 7 $ , inclusive.)
The bishop attacks in all directions diagonally, and there is no limit to the distance which the bishop can attack. Note that the cell on which the bishop is placed is also considered attacked.
 An example of a bishop on a chessboard. The squares it attacks are marked in red.Mihai has marked all squares the bishop attacks, but forgot where the bishop was! Help Mihai find the position of the bishop.
An example of a bishop on a chessboard. The squares it attacks are marked in red.Mihai has marked all squares the bishop attacks, but forgot where the bishop was! Help Mihai find the position of the bishop.
输入格式
The first line of the input contains a single integer $ t $ ( $ 1 \leq t \leq 36 $ ) — the number of test cases. The description of test cases follows. There is an empty line before each test case.
Each test case consists of $ 8 $ lines, each containing $ 8 $ characters. Each of these characters is either ‘#’ or ‘.’, denoting a square under attack and a square not under attack, respectively.
输出格式
For each test case, output two integers $ r $ and $ c $ ( $ 2 \leq r, c \leq 7 $ ) — the row and column of the bishop.
The input is generated in such a way that there is always exactly one possible location of the bishop that is not on the edge of the board.
样例 #1
样例输入 #1
3.....#..
#...#...
.#.#....
..#.....
.#.#....
#...#...
.....#..
......#.#.#.....
.#......
#.#.....
...#....
....#...
.....#..
......#.
.......#.#.....#
..#...#.
...#.#..
....#...
...#.#..
..#...#.
.#.....#
#.......
样例输出 #1
4 3
2 2
4 5
提示
The first test case is pictured in the statement. Since the bishop lies in the intersection row $ 4 $ and column $ 3 $ , the correct output is 4 3.
代码实现
遍历每一个点看他的四个角和本身是不是"#"即可
#include<bits/stdc++.h>
using namespace std;const int maxn=20;
int t;
char a[maxn][maxn];
inline bool inbound(int x,int y){return x>=1&&x<=8&&y>=1&&y<=8;}
int main(){scanf("%d",&t);while(t--){for(int i=1;i<=8;i++){for(int j=1;j<=8;j++)scanf(" %c",&a[i][j]);}bool flag=false;for(int i=1;i<=8;i++){for(int j=1;j<=8;j++){if(a[i][j]=='#'&&a[i-1][j+1]=='#'&&a[i-1][j-1]=='#'&&a[i+1][j-1]=='#'&&a[i+1][j+1]=='#'){printf("%d %d\n",i,j);break;}}if(flag)break;}}return 0;
}
相关文章:

CF1692C Where‘s the Bishop? 题解
CF1692C Wheres the Bishop? 题解题目链接字面描述题面翻译题目描述题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示代码实现题目 链接 https://www.luogu.com.cn/problem/CF1692C 字面描述 题面翻译 题目描述 有一个888\times888的棋盘,列编号从…...
Jenkins集成Allure报告
Jenkins集成Allure报告 紧接上文:Jenkins部署及持续集成——傻瓜式教程 使用Allure报告 1、在插件库下载Allure插件Allure Jenkins Plugin 2、在构建后操作中加入allure执行的报告目录(相对于项目的路径) 3、run.py代码改成如下 import p…...
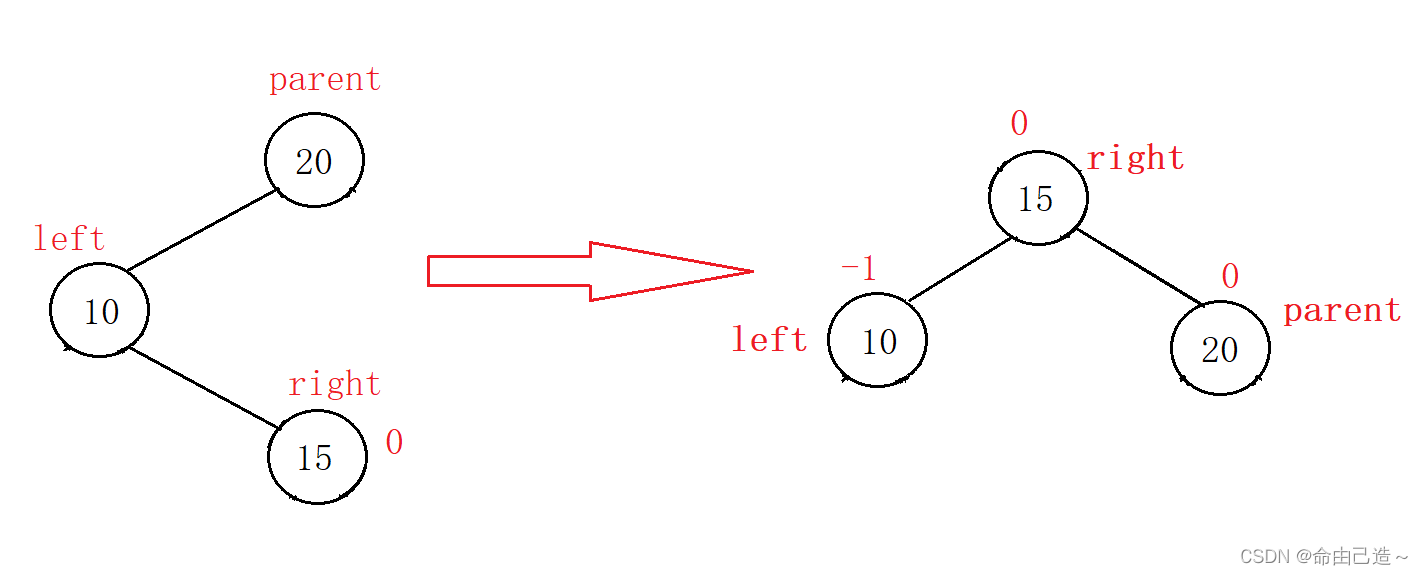
【数据结构】AVL树
AVL树一、AVL树的概念二、AVL的接口2.1 插入2.2 旋转2.2.1 左单旋2.2.2 右单旋2.2.3 左右双旋2.2.4 右左双旋三、验证四、源码一、AVL树的概念 当我们用普通的搜索树插入数据的时候,如果插入的数据是有序的,那么就退化成了一个链表,搜索效率…...

这一次我不再低调,老板法拉利的车牌有我的汗水
起源: 5Why分析法最初是由丰田佐吉提出的,后来,丰田汽车公司在发展完善其制造方法学的过程中持续采用该方法。5Why分析法作为丰田生产系统的入门课程之一,是问题求解的关键培训课程。丰田生产系统的设计师大野耐一曾将5Why分析法描述为:“丰田科学方法的基础,重复五次,问…...

通过连接另一个数组的子数组得到一个数组
给你一个长度为 n 的二维整数数组 groups ,同时给你一个整数数组 nums 。 你是否可以从 nums 中选出 n 个 不相交 的子数组,使得第 i 个子数组与 groups[i] (下标从 0 开始)完全相同,且如果 i > 0 ,那么…...

公派访问学者的申请条件
知识人网海外访问学者申请老师为大家分享公派访问学者申请的基本条件以及哪些人员的申请是暂不受理的,供大家参考:一、 申请人基本条件:1.热爱社会主义祖国,具有良好的思想品德和政治素质,无违法违纪记录。2.具有良好专…...
多点电容触摸屏实验
目录 一、简介 二、硬件原理 编辑1、CT_INT 2、I2C2_SCL和I2C2_SDA 3、RESET复位引脚 三、FT54x6/FT52x6电容触摸芯片 四、代码编写 1、编写ft5426.h 2、编写ft5426.c 3、main函数 一、简介 电容屏只需要手指轻触即可,而电阻屏是需要手指给予一定的压力才…...

【算法与数据结构(C语言)】栈和队列
文章目录 目录 前言 一、栈 1.栈的概念及结构 2.栈的实现 入栈 出栈 获取栈顶元素 获取栈中有效元素个数 检测栈是否为空,如果为空返回非零结果,如果不为空返回0 销毁栈 二、队列 1.队列的概念及结构 2.队列的实现 初始化队列 队尾入队列 队头出队列 获…...
Uni-app使用vant和uview组件
目录 1.安装vant组件 1.1安装前需知 1.2.安装 1.3.创建uni-app项目 2.安装uview-ui组件 2.1官网 2.2安装 2.3安装成功 1.安装vant组件 1.1安装前需知 小程序能使用vant-weapp组件,且官网的安装是直接导入小程序中,不能直接导入uni-app框架中 V…...
2023年PMP考试应该注意些什么?
首先注意(报考条件) 2023年PMP考试报名流程: 一、PMP英文报名: 英文报名时间无限制,随时可以报名,但有一年的有效期,所以大家尽量提前报名,在英文报名有效期内进行中文报名。 英…...
selenium环境安装及使用
selenium简介官网https://www.selenium.dev简介用于web浏览器测试的工具支持的浏览器包括IE,Firefox,Chrome,edge等使用简单,可使用java,python等多种语言编写用例脚本主要由三个工具构成,webdriver,IDE,web自动化环境…...
高性能低功耗4口高速USB2.0 HUB 完美替代FE1.1S和FE8.1
该NS1.1s是一个高度集成的,高品质,高性能,低功耗,为USB 2.0高速4端口集线器又低成本的解决方案。 (点击即可咨询芯片详细信息) NS1.1s的特点 1.通用串行总线规范修订版2.0(USB 2.0)完…...
Go全栈学习(一)基础语法
Go语言基础语法 文章目录Go语言基础语法注释变量变量的定义变量的交换理解变量(内存地址)匿名变量变量的作用域常量2023.2.4日 总结// 关于Goland 中 执行的问题// 1、包下执行 (一个 main 函数来执行,如果有多个,无法…...
centos7搭建svn配置
基本概述 Apache Subversion(简称SVN,svn),一个开放源代码的版本控制系统,相较于RCS、CVS,它采用了分支管理系统,它的设计目标就是取代CVS。互联网上很多版本控制服务已从CVS转移到Subversion。…...
趣味三角——第12章——tanx
第12章节 tanx In his very numerous memoires, and especially in his great work, Introductio in analysin infinitorum (1748), Euler displayed the most wonderful skill in obtaining a rich harvest of results of great interest. . . . Hardly any other work …...
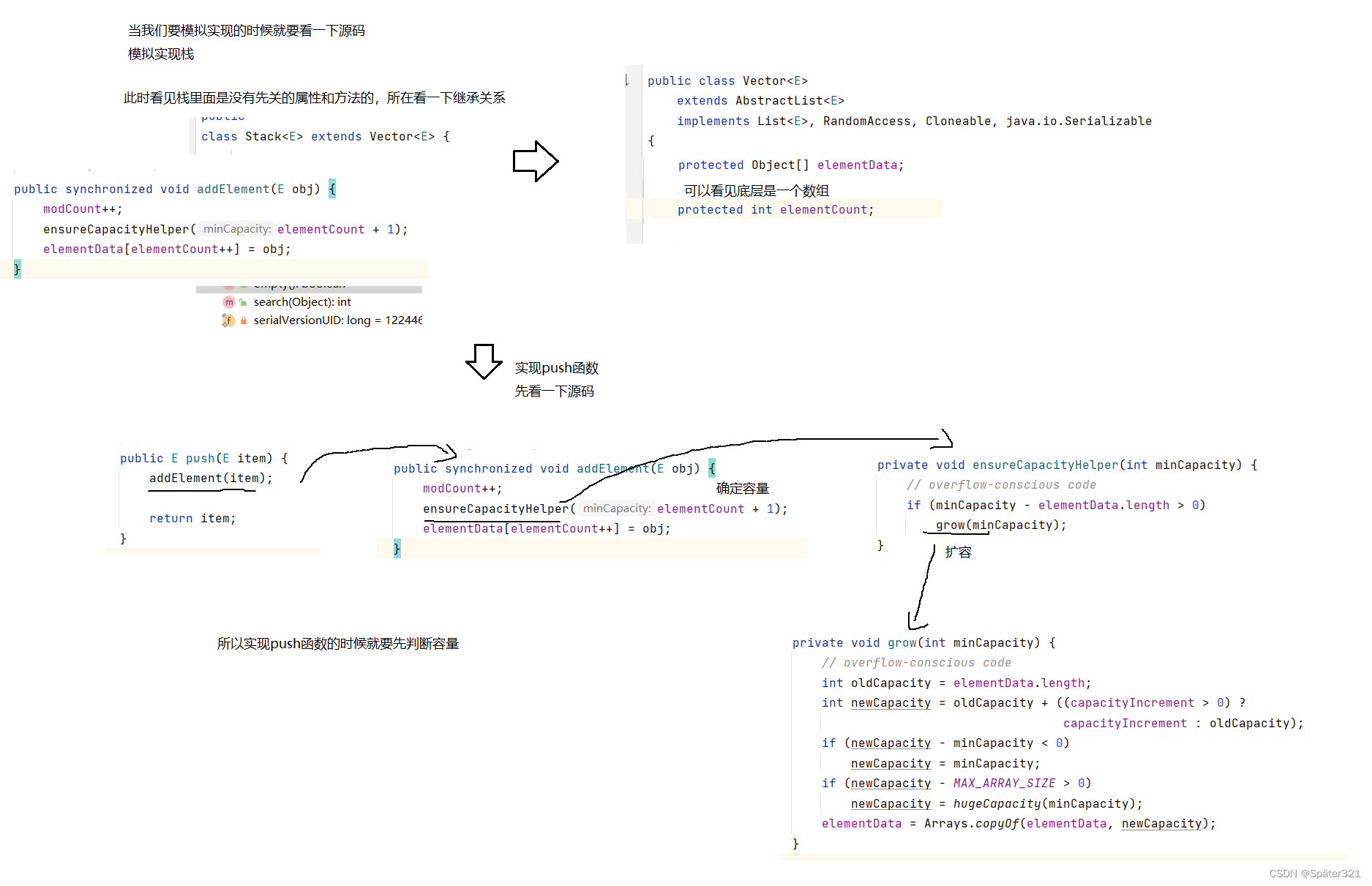
Java - 数据结构,栈
一、栈 1.1、什么是栈 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈 顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。 压…...
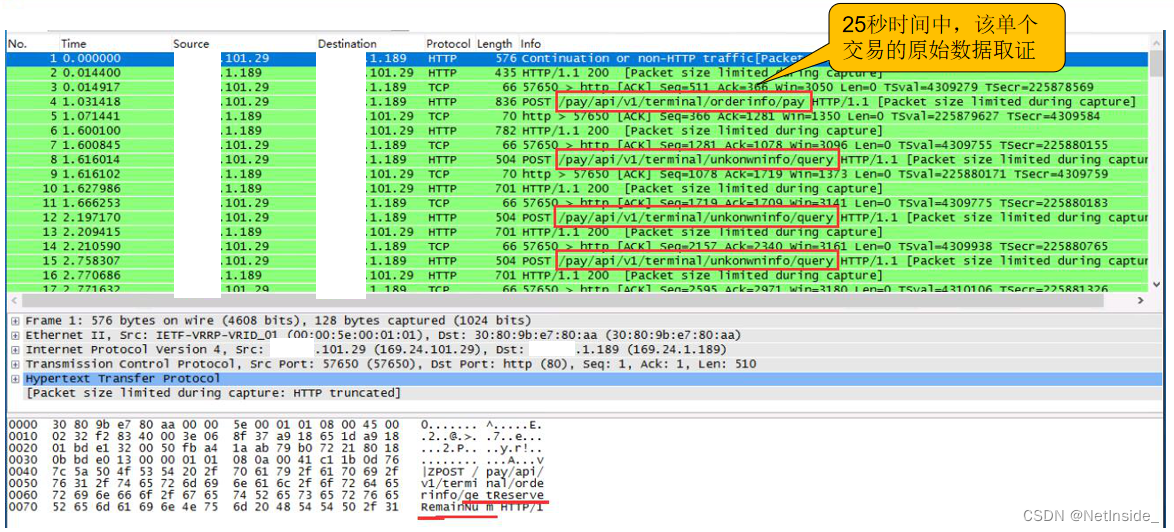
某餐厅系统网络故障分析案例
背景 针对食堂经营企业,某堂食软件为客户提供优化堂食就餐流程、提高食堂服务水平和管理效率。 某上海客户使用该堂食系统,在就餐高峰时段,总是出现支付、点餐等操作缓慢,动辄一个操作需要等待几十秒。该客户联系软件厂商&#…...

华为OD机试题,用 Java 解【密室逃生游戏】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

如何重命名SQL Server数据库
重命名SQL Server数据库 使用T-SQL重命名SQL Server数据库使用分离和附加重命名SQL Server数据库使用T-SQL查询分离和重新连接在SSMS中分离和重新连接通过SSMS重命名SQL Server数据库当使用SQL数据库很长一段时间时,你可能会遇到需要为数据库命名的情况。它可以用几种不同的方…...

联想昭阳E5-ITL电脑开机后绿屏怎么U盘重装系统?
联想昭阳E5-ITL电脑开机后绿屏怎么U盘重装系统?有用户电脑正常开机之后,出现了屏幕变成绿屏,无法进行操作的情况。这个问题是系统出现了问题,那么如何去进行问题的解决呢?接下来我们一起来分享看看如何使用U盘重装电脑…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
