最短路径专题6 最短路径-多路径
题目: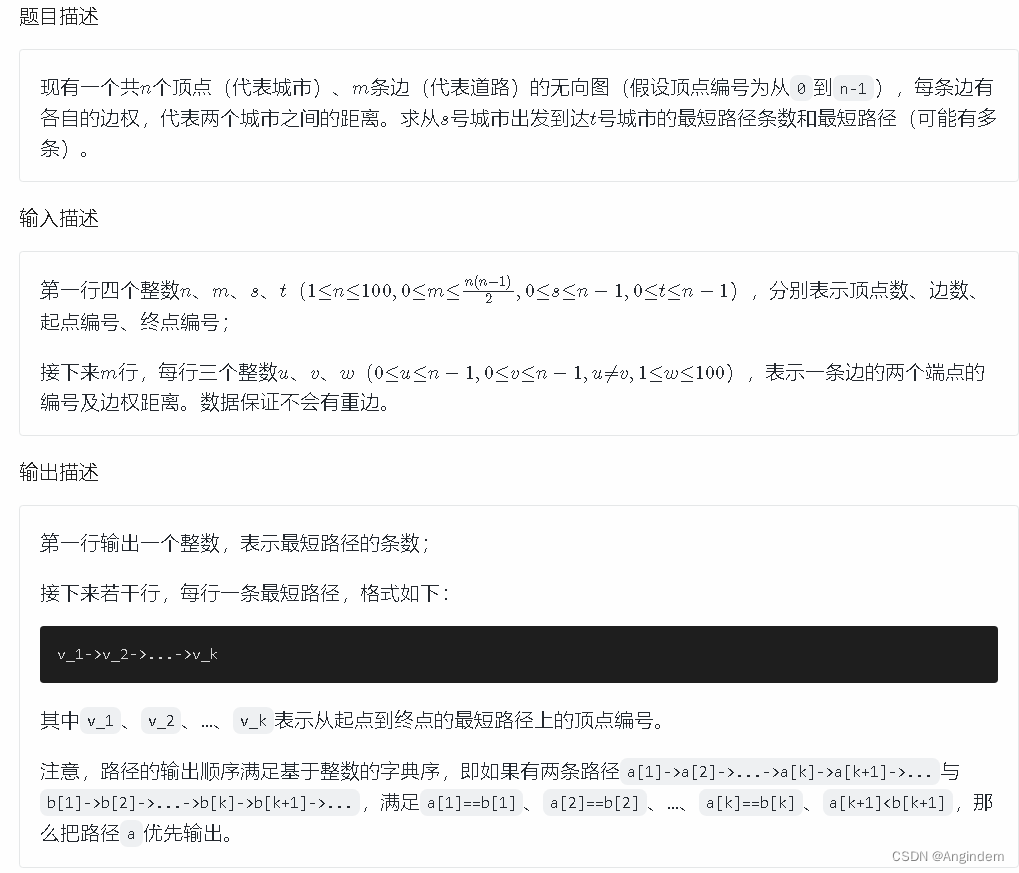
样例:
|
|
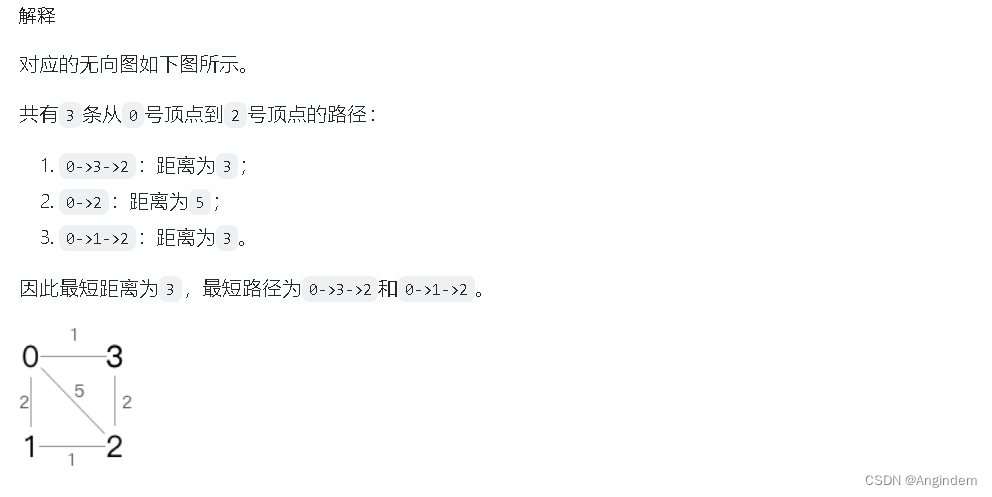
思路:
根据题意,最短路模板还是少不了的,
我们要添加的是,
记录各个结点有多少个上一个结点走动得来的,由于更新了最短路径,需要清空之前的记录的结点,重新记录当前结点由哪上一个结点得来的;
当遇到相同的最短路距离的时候,直接添加 j 结点也由 当前结点得来的。
最后递归遍历各个结点路径,并存储好,输出即可。
代码详解如下:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>
#define endl '\n'
#define x first
#define y second
#define mk make_pair
#define int long long
#define NO puts("NO")
#define YES puts("YES")
#define umap unordered_map
#define INF 0x3f3f3f3f3f3f3f3f
#define All(x) (x).begin(),(x).end()
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;
using PII = pair<int,int>;int n,k,start,last;int dist[N];
bool st[N];// 建立链表
int h[N],e[N],w[N],ne[N],idx;
inline void Add(int a,int b,int c)
{e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx++;
}vector<int>tree[N]; // 记录每个结点拥有哪些结点得来的inline void Dijkstra()
{memset(dist,INF,sizeof dist);dist[start] = 0;priority_queue<PII,vector<PII>,greater<PII>>q;q.push(mk(0,start));while(q.size()){PII now = q.top();q.pop();int a = now.y;int dis = now.x;if(st[a]) continue;st[a] = true;for(int i = h[a];i != -1;i = ne[i]){int j = e[i];if(dist[j] > dis + w[i]){dist[j] = dis + w[i];tree[j].clear(); // 更新了最短路径,所以清空上一个结点记录过的多个结点 路径tree[j].emplace_back(a); // j 结点记录 添加 a 结点得来的路径}else // 如果遇到相同最短路距离,j 结点 添加 当前的 a 结点路径if(dist[j] == dis + w[i]) tree[j].emplace_back(a);// 记录该结点,方便下一次的走动q.push(mk(dist[j],j));}}return ;
}vector<vector<int>>paths; // 记录多个路径
vector<int>tempPath; // 临时路径void getPath(int now)
{// 到达递归边界,开始回溯取各个路径if(now == start){tempPath.emplace_back(now); // 临时路径存储当前结点paths.emplace_back(tempPath); // 存储路径tempPath.pop_back(); // 弹出存储的当前结点,进行回溯,寻找另一条不同的路径return ;}tempPath.emplace_back(now); // 临时路径存储当前结点// 遍历 当前结点 now 由哪个结点得来的// 递归获取路径结点for(auto i : tree[now]){getPath(i);}tempPath.pop_back(); // 弹出存储的当前结点,进行回溯,寻找另一条不同的路径return ;
}inline void solve()
{// 初始化链表memset(h,-1,sizeof h);cin >> n >> k >> start >> last;while(k--){int a,b,c;cin >> a >> b >> c;Add(a,b,c);Add(b,a,c);}// 求最短路径Dijkstra();// 获取最短路径getPath(last);int sum = paths.size(); // 总的路径数量// 翻转获得的全部路径,由于我们是从终点往后获取的// 所以需要翻转一下for(int i = 0;i < sum;++i){reverse(All(paths[i]));}// 根据题意,字典序排序好每条路径sort(All(paths));// 输出路径条数cout << sum << endl;// 输出记录的每条最短路路径for(int i = 0;i < sum;++i){bool rem = false; // 控制格式for(int j : paths[i]){if(rem) cout << "->";cout << j;rem = true;}cout << endl;}
}
signed main()
{
// freopen("a.txt", "r", stdin);___G;int _t = 1;
// cin >> _t;while (_t--){solve();}return 0;
}最后提交:
相关文章:

最短路径专题6 最短路径-多路径
题目: 样例: 输入 4 5 0 2 0 1 2 0 2 5 0 3 1 1 2 1 3 2 2 输出 2 0->1->2 0->3->2 思路: 根据题意,最短路模板还是少不了的, 我们要添加的是, 记录各个结点有多少个上一个结点走动得来的…...

【Linux】Linux常用命令—文件管理(上)
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 🔥c系列专栏:C/C零基础到精通 🔥 给大…...
【Python】基于OpenCV人脸追踪、手势识别控制的求生之路FPS游戏操作
【Python】基于OpenCV人脸追踪、手势识别控制的求生之路FPS游戏操作 文章目录 手势识别人脸追踪键盘控制整体代码附录:列表的赋值类型和py打包列表赋值BUG复现代码改进优化总结 py打包 视频: 基于OpenCV人脸追踪、手势识别控制的求实之路FPS游戏操作 手…...
约束优化算法(optimtool.constrain)
import optimtool as oo from optimtool.base import np, sp, pltpip install optimtool>2.4.2约束优化算法(optimtool.constrain) import optimtool.constrain as oc oc.[方法名].[函数名]([目标函数], [参数表], [等式约束表], [不等式约数表], [初…...
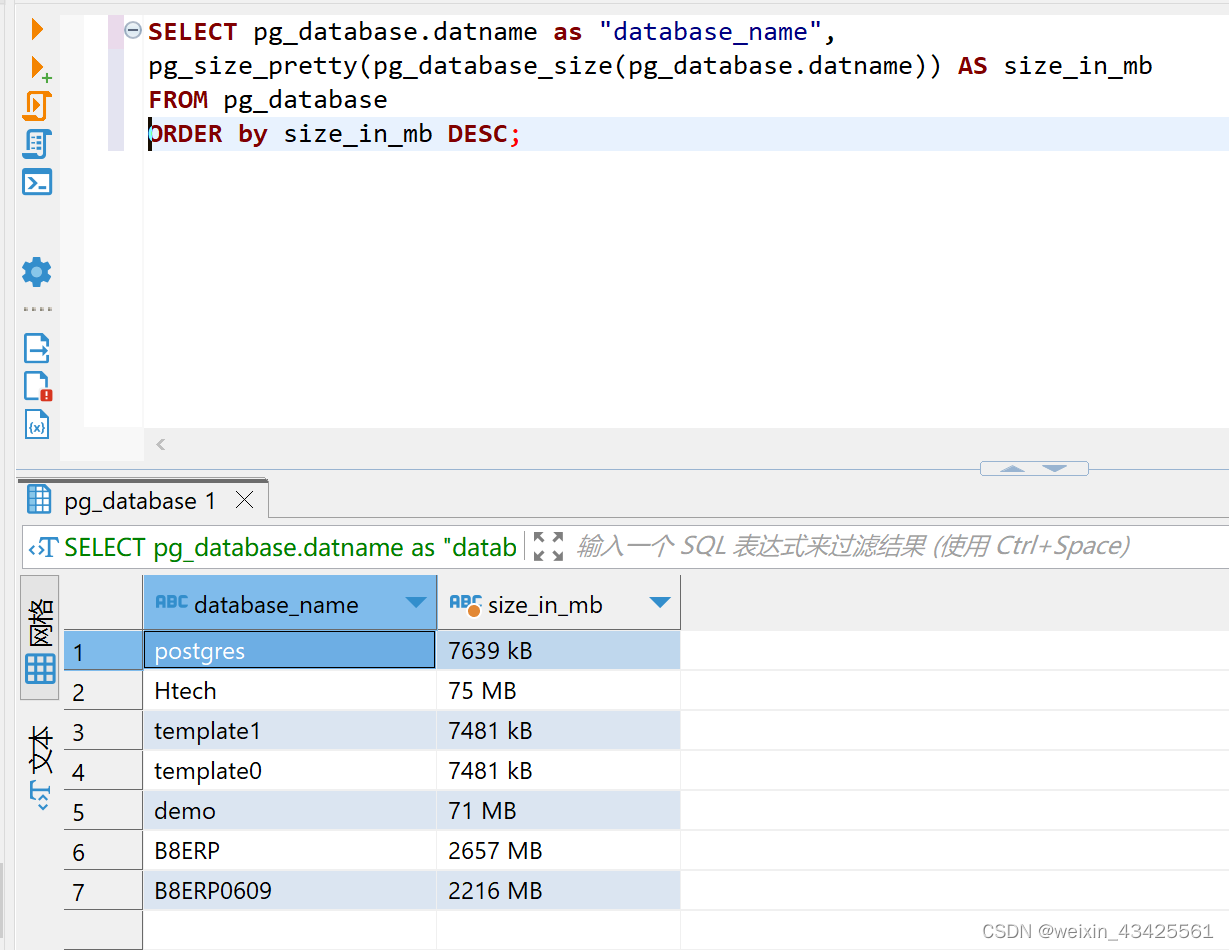
如何查看postgresql中的数据库大小?
你可以使用以下命令来查看PostgreSQL数据库的大小: SELECT pg_database.datname as "database_name", pg_size_pretty(pg_database_size(pg_database.datname)) AS size_in_mb FROM pg_database ORDER by size_in_mb DESC;这将返回一个表格࿰…...

使用python-opencv检测图片中的人像
最简单的方法进行图片中的人像检测 使用python-opencv配合yolov3模型进行图片中的人像检测 1、安装python-opencv、numpy pip install opencv-python pip install numpy 2、下载yolo模型文件和配置文件: 下载地址: https://download.csdn.net/down…...

项目进展(三)-电机驱动起来了,发现了很多关键点,也遇到了一些低级错误,
一、前言 昨天电机没有驱动起来,头发掉一堆,不过今天,终于终于终于把电机驱动起来了!!!!,特别开心,哈哈哈哈,后续继续努力完善!!&…...
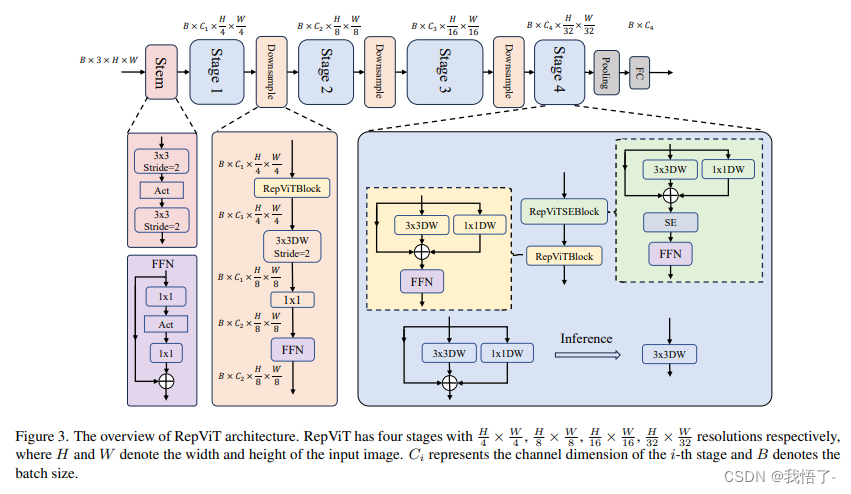
目标检测算法改进系列之Backbone替换为RepViT
RepViT简介 轻量级模型研究一直是计算机视觉任务中的一个焦点,其目标是在降低计算成本的同时达到优秀的性能。轻量级模型与资源受限的移动设备尤其相关,使得视觉模型的边缘部署成为可能。在过去十年中,研究人员主要关注轻量级卷积神经网络&a…...

学习 Kubernetes的难点和安排
Kubernetes 技术栈的特点可以用四个字来概括,那就是“新、广、杂、深”: 1.“新”是指 Kubernetes 用到的基本上都是比较前沿、陌生的技术,而且版本升级很快,经常变来变去。 2.“广”是指 Kubernetes 涉及的应用领域很多、覆盖面非…...

【MATLAB源码-第42期】基于matlab的人民币面额识别系统(GUI)。
操作环境: MATLAB 2022a 1、算法描述 基于 MATLAB 的人民币面额识别系统设计可以分为以下步骤: 1. 数据收集与预处理 数据收集: 收集不同面额的人民币照片,如 1 元、5 元、10 元、20 元、50 元和 100 元。确保在不同环境、不…...
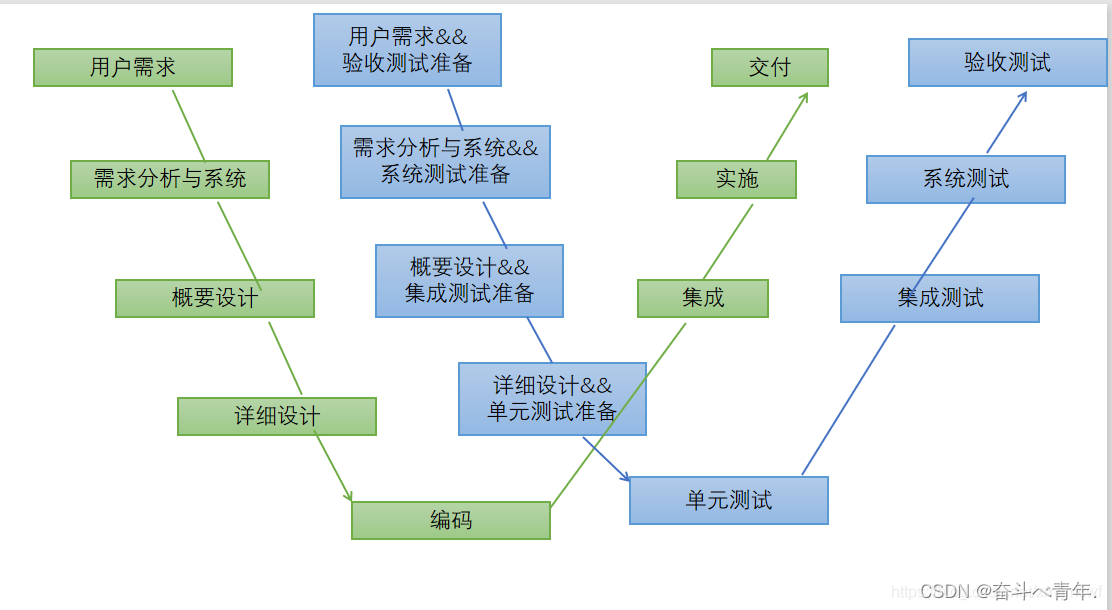
【软件测试】软件测试的基础概念
一、一个优秀的测试人员需要具备的素质 技能方面: 优秀的测试用例设计能力:测试用例设计能力是指,无论对于什么类型的测试,都能够设计出高效的发现缺陷,保证产品质量的优秀测试用例。这就需要我们掌握设计测试用例的方…...
Docker-mysql,redis安装
安装MySQL 下载MySQL镜像 终端运行命令 docker pull mysql:8.0.29镜像下载完成后,需要配置持久化数据到本地 这是mysql的配置文件和存储数据用的目录 切换到终端,输入命令,第一次启动MySQL容器 docker run --restartalways --name mysq…...

五种I/O模型
目录 1、阻塞IO模型2、非阻塞IO模型3、IO多路复用模型4、信号驱动IO模型5、异步IO模型总结 blockingIO - 阻塞IOnonblockingIO - 非阻塞IOIOmultiplexing - IO多路复用signaldrivenIO - 信号驱动IOasynchronousIO - 异步IO 5种模型的前4种模型为同步IO,只有异步IO模…...

用nativescript开发ios程序常用命令?
NativeScript是一个用于跨平台移动应用程序开发的开源框架,允许您使用JavaScript或TypeScript构建原生iOS和Android应用程序。以下是一些常用的NativeScript命令,用于开发iOS应用程序: 1、创建新NativeScript项目: tns create m…...
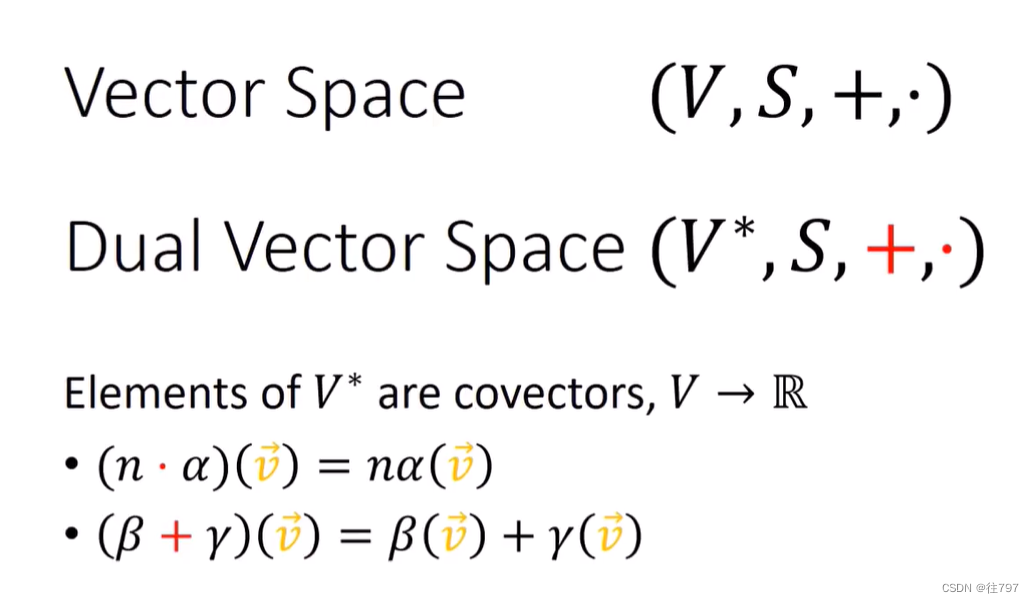
6.Tensors For Beginners-What are Convector
Covectors (协向量) What‘s a covector Covectors are “basically” Row Vectors 在一定程度上,可认为 协向量 基本上就像 行向量。 但不能简单地认为 这就是列向量进行转置! 行向量 和 列向量 是根本不同类型的对象。 …...
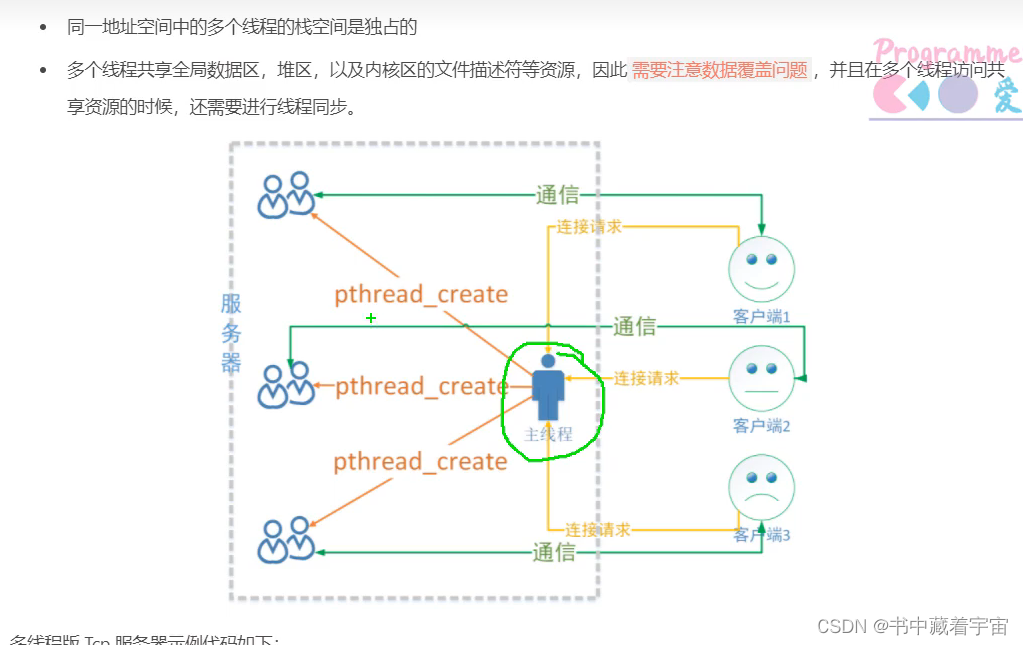
Linux多线程网络通信
思路:主线程(只有一个)建立连接,就创建子线程。子线程开始通信。 共享资源:全局数据区,堆区,内核区描述符。 线程同步不同步需要取决于线程对共享资源区的数据的操作,如果是只读就不…...

矩阵的c++实现(2)
上一次我们了解了矩阵的运算和如何使用矩阵解决斐波那契数列,这一次我们多看看例题,了解什么情况下用矩阵比较合适。 先看例题 1.洛谷P1939 【模板】矩阵加速(数列) 模板题应该很简单。 补:1<n<10^9 10^9肯定…...

RPC 框架之Thrift入门(一)
📋 个人简介 💖 作者简介:大家好,我是阿牛,全栈领域优质创作者。😜📝 个人主页:馆主阿牛🔥🎉 支持我:点赞👍收藏⭐️留言Ὅ…...
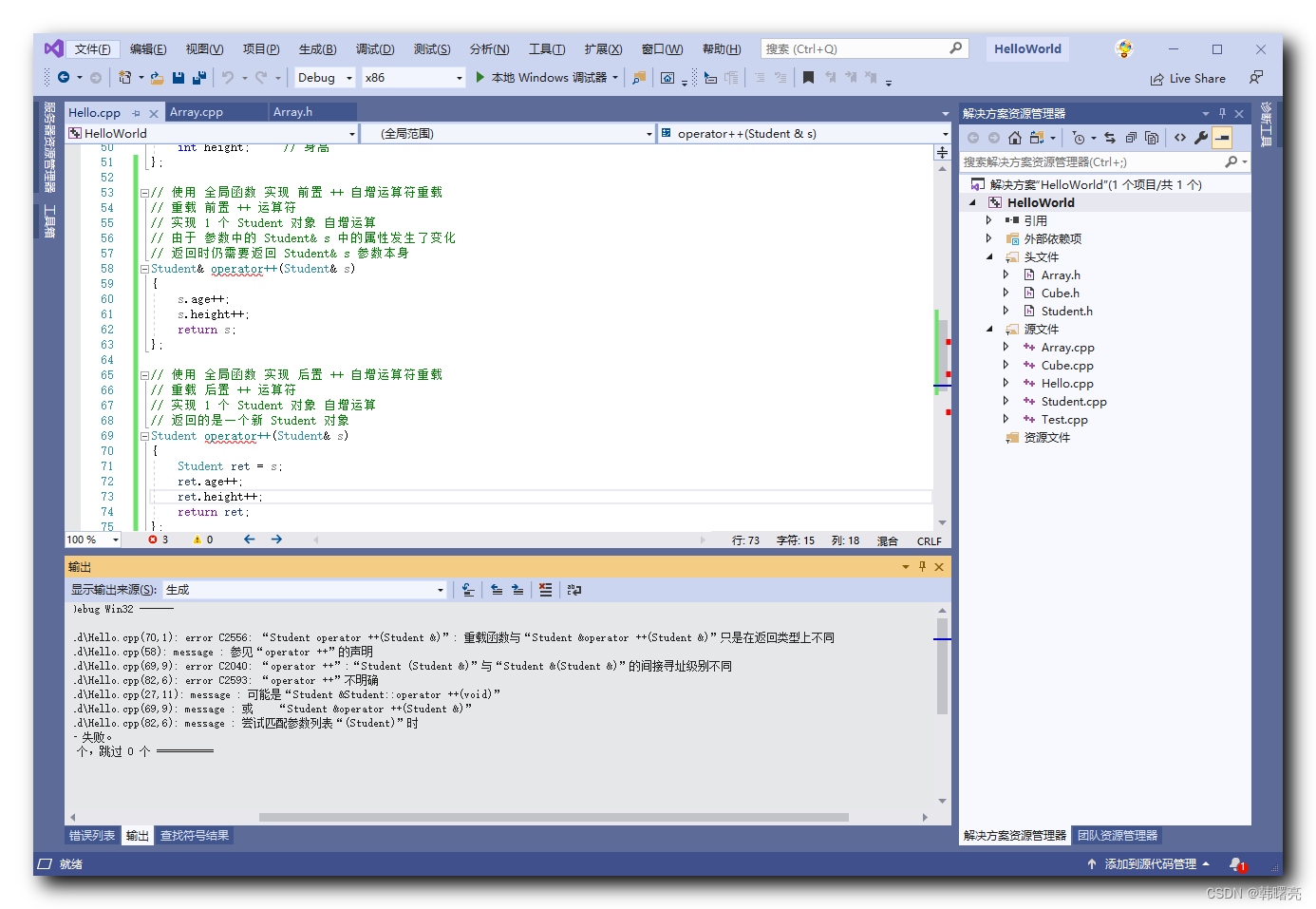
【C++】运算符重载 ⑥ ( 一元运算符重载 | 后置运算符重载 | 前置运算符重载 与 后置运算符重载 的区别 | 后置运算符重载添加 int 占位参数 )
文章目录 一、后置运算符重载1、前置运算符重载 与 后置运算符重载 的区别2、后置运算符重载添加 int 占位参数 上 2 2 2 篇博客 【C】运算符重载 ④ ( 一元运算符重载 | 使用 全局函数 实现 前置 自增运算符重载 | 使用 全局函数 实现 前置 - - 自减运算符重载 )【C】运算符…...

538. 把二叉搜索树转换为累加树
题目描述 给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。 提醒一下,二叉搜索树满足下列约束…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...

6.9本日总结
一、英语 复习默写list11list18,订正07年第3篇阅读 二、数学 学习线代第一讲,写15讲课后题 三、408 学习计组第二章,写计组习题 四、总结 明天结束线代第一章和计组第二章 五、明日计划 英语:复习l默写sit12list17&#…...
