【数据结构与算法】树、二叉树的概念及结构(详解)
前言:
💥🎈个人主页:Dream_Chaser~ 🎈💥
✨✨专栏:http://t.csdn.cn/oXkBa
⛳⛳本篇内容:c语言数据结构--树以及二叉树的概念与结构

目录
一.树概念及结构
1.树的概念
1.1树与非树
树的特点:
非树(图)的特点:
1.2 关于树的细致概念
1.3树的表示
1.4树在实际中的运用(表示文件系统的目录树结构)
二.二叉树概念及结构
1.概念
2.现实中的二叉树:
2.3特殊的二叉树:
2.4 二叉树的性质
证明性质2和1
习题练习
一.树概念及结构
1.树的概念
树是一种 非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。

1.1树与非树

树的特点:
- 有一个特殊的结点,称为根结点,根节点没有前驱结点(没有父节点)
下面的两点一起理解:
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。
可以理解为:
由根节点指向了各子树,子树的双亲节点又可以作为根节点,指向它们的孩子节点
非树(图)的特点:


注意:树形结构中,子树之间不能有交集,否则就不是树形结构
3.一棵N个结点的树有N-1条边

1.2 关于树的细致概念
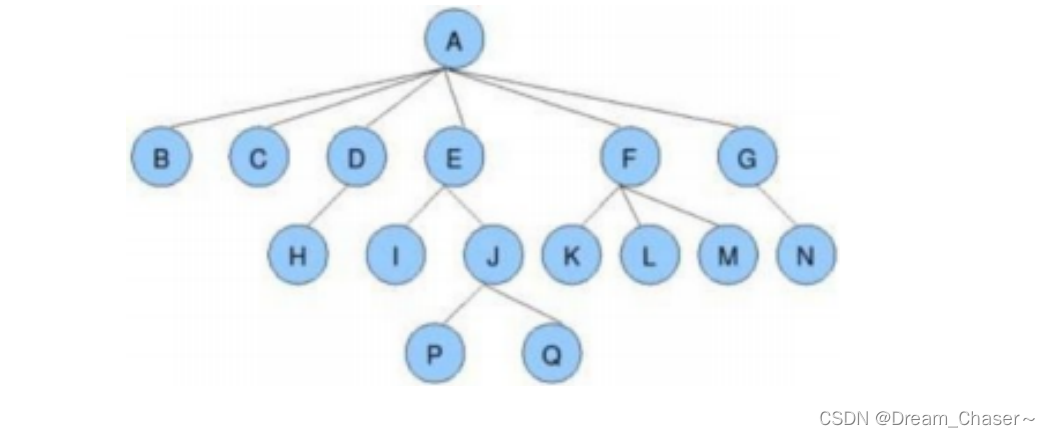
下面有个✅的是比较重要的知识点
✅节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
✅叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
✅非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
✅双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
✅孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
✅兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
✅树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
✅节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
✅子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林
对各知识点的进一步画图解析:
- 节点的度:与该节点直接相连的边的数量

- 叶节点(终端节点):度为0的节点
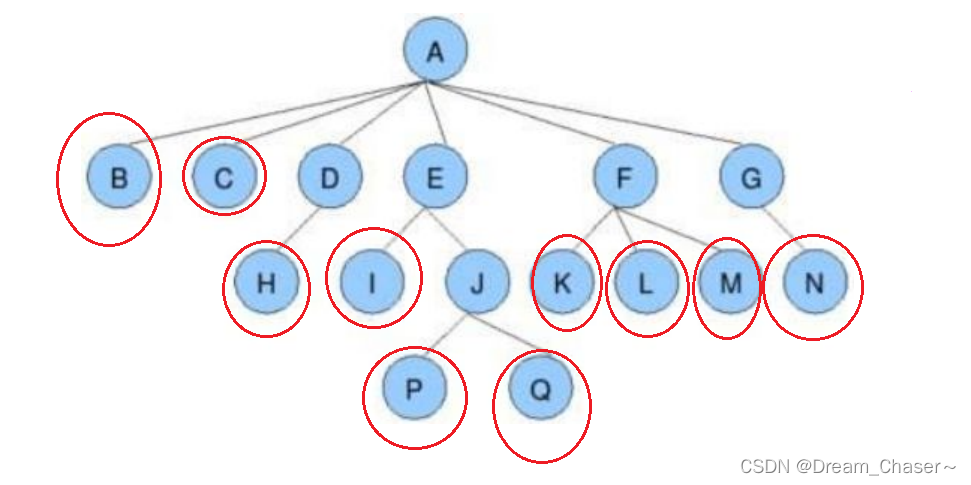
- 分支节点(非终端节点):度不为0的节点

- 父节点(双亲节点):一个节点的直接前驱就是它的父节点

- 子节点(孩子节点):一个节点的直接后继就是它的子节点

- 兄弟节点:由同一个父节点生出来的都是互为兄弟节点

- 树的度:一棵树中,最大的节点的度称为树的度
- 节点的层次:从上往下数,从根开始定义起,根为第1层,根的子节点为第2层,以此类推;(默认是从1开始)
- 树的高度(深度):树中节点的最大层次,下图的高度就是4

- 节点的高度:从下往上数
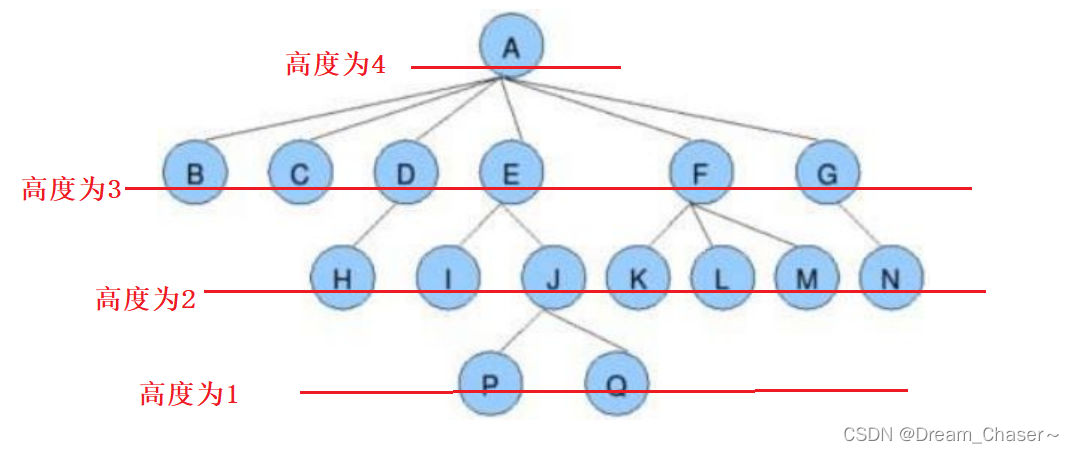
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟
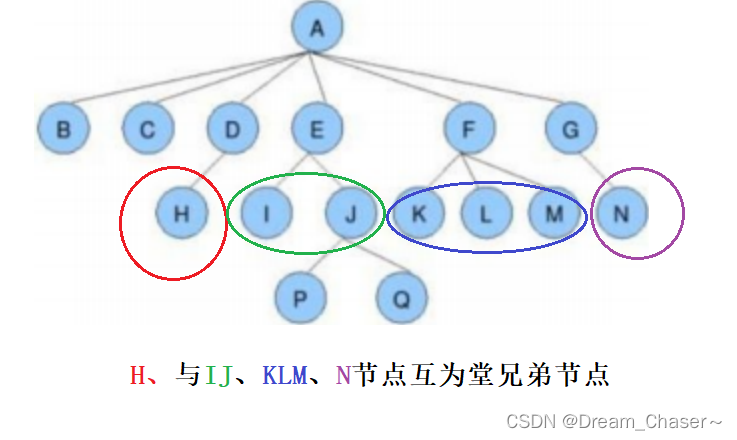
- 节点的祖先:指从该节点向上追溯到根节点的路径上的所有节点,包括该节点的父节点、父节点的父节点,以此类推,直到达到根节点为止。
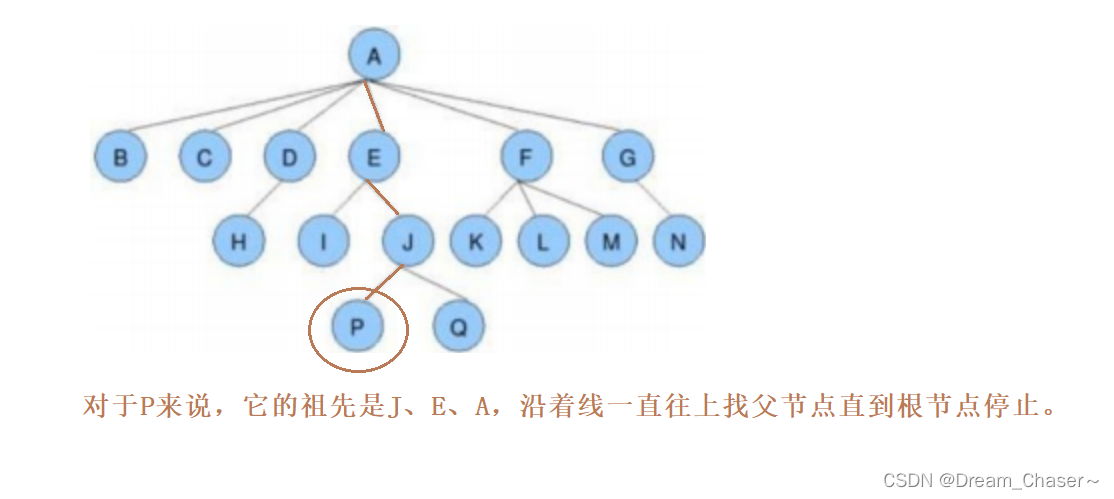
- 子孙:从该节点向下追溯到所有末端节点的路径上的所有节点,包括该节点的直接子节点、子节点的子节点,以此类推,直到达到叶子节点为止。

- 森林:是由多个不相交的树组成的集合(并查集)
1.3树的表示

B、顺序表存储孩子。

C、双亲表示法。(每个位置只存双亲的指针或者下标)

D、左孩子右兄弟表示法--简化树结构定义
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};画图解析:

1.4树在实际中的运用(表示文件系统的目录树结构)

二.二叉树概念及结构
1.概念
一棵二叉树是结点的一个有限集合,该集合:1. 或者为空2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
 从上图可以看出:
从上图可以看出:
1. 二叉树不存在度大于2的结点(度为0也可以)2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树注意:对于任意的二叉树都是由以下几种情况复合而成的:
2.现实中的二叉树:

2.3特殊的二叉树:
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是 说,如果一个二叉树的层数为K,且结点总数是2^k-1 ,则它就是满二叉树。2.完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

2.4 二叉树的性质
1. 若 i>0 , i 位置节点的双亲序号: (i-1)/2 ; i=0 , i 为根节点编号,无双亲节点2. 若 2i+1<n ,左孩子序号: 2i+1 , 2i+1>=n 否则无左孩子3. 若 2i+2<n ,右孩子序号: 2i+2 , 2i+2>=n 否则无右孩子
证明性质2和1

习题练习
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( B)A 不存在这样的二叉树B 200C 198D 199解析: 2.下列数据结构中,不适合采用顺序存储结构的是( A)A 非完全二叉树B 堆C 队列D 栈解析:顺序存储结构适合于具有连续存储空间的数据结构,其中元素按照线性顺序存储。 对于非完全二叉树,由于其结构不规则,无法通过连续的存储空间来表示。因此,非完全二叉树不适合采用顺序存储结构。B. 堆、C. 队列、D. 栈都可以通过顺序存储结构有效地实现。堆是一种完全二叉树,可以使用数组来表示。队列和栈可以使用数组或者链表来表示,都适合顺序存储结构。3.在具有 2n 个结点的完全二叉树中,叶子结点个数为(A )A nB n+1C n-1D n/2
2.下列数据结构中,不适合采用顺序存储结构的是( A)A 非完全二叉树B 堆C 队列D 栈解析:顺序存储结构适合于具有连续存储空间的数据结构,其中元素按照线性顺序存储。 对于非完全二叉树,由于其结构不规则,无法通过连续的存储空间来表示。因此,非完全二叉树不适合采用顺序存储结构。B. 堆、C. 队列、D. 栈都可以通过顺序存储结构有效地实现。堆是一种完全二叉树,可以使用数组来表示。队列和栈可以使用数组或者链表来表示,都适合顺序存储结构。3.在具有 2n 个结点的完全二叉树中,叶子结点个数为(A )A nB n+1C n-1D n/2和节点个数相关的公式有二:
n0 = n2 + 1,N = n0 + n1 + n2
已知总个数N为2n,那么只要知道n1即可求出n0.
这里有一个重要的结论:
在完全二叉树中,如果节点总个数为奇数,则没有度为1的节点;如果节点总个数为偶数,只有一个度为1的节点。
节点个数是偶数,只有一个度为1的节点
节点个数是奇数,没有度为1的节点
2n为偶数,因此有一个度为1的节点。
2n = n0 + 1 + n2 = n0 + 1 + n0 - 1
2n = 2n0
n0 = n,故选A
4.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( B)A 11B 10C 8D 12解析:根据性质4,h=log2(n+1),n=531,h = log2(532),找一个最接近的数就是log2(512),也就是log2(2^9),向上取整,n=10;5.一个具有767个节点的完全二叉树,其叶子节点个数为(B)A 383B 384C 385D 386解析:N=767个节点数是奇数个,所以N= n0+ n2(奇数个没有度为1的节点) ,由n0 = n2+1; N = 2n0 - 1 ,那么n0 = (N + 1) / 2 = 384
相关文章:

【数据结构与算法】树、二叉树的概念及结构(详解)
前言: 💥🎈个人主页:Dream_Chaser~ 🎈💥 ✨✨专栏:http://t.csdn.cn/oXkBa ⛳⛳本篇内容:c语言数据结构--树以及二叉树的概念与结构 目录 一.树概念及结构 1.树的概念 1.1树与非树 树的特点࿱…...
)
函数指针数组指针(指向函数指针数组的指针)
一、什么是函数指针数组指针? 本质是指针,指向函数指针数组,存放函数指针数组的地址。 代码如下: pfArr是函数指针数组 p是函数指针数组指针 int main() {int(*pfArr[])(int, int) { Add,Sub };//函数指针数组int(*(*p)[])(int, …...

经典算法-----汉诺塔问题
前言 今天我们学习一个老经典的问题-----汉诺塔问题,可能在学习编程之前我们就听说过这个问题,那这里我们如何去通过编程的方式去解决这么一个问题呢?下面接着看。 汉诺塔问题 问题描述 这里是引用汉诺塔问题源自印度一个古老的传说&#x…...
博客之站项目测试报告
项目背景项目功能测试计划Bug总结升级自动化测试正常登录流程 项目背景 1:博客之站系统是采用前后端分离的方式来实现;使用MySQL、Redis数据库储存相关数据;同时部署到云服务器上。 2:包含注册页、登录页、博客列表页、个人列表页…...

k8s晋级之管理容器的计算资源
概述 在 Kubernetes 中创建工作负载时,您可以为 Pod 中的每一个容器指定其所需要的内存(RAM)大小和 CPU 数量。如果这些信息被指定了,Kubernetes 调度器可以更好的决定将 Pod 调度到哪一个节点。对于容器来说,其所需要…...

计算机竞赛 深度学习火车票识别系统
文章目录 0 前言1 课题意义课题难点: 2 实现方法2.1 图像预处理2.2 字符分割2.3 字符识别部分实现代码 3 实现效果4 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 图像识别 火车票识别系统 该项目较为新颖,适…...
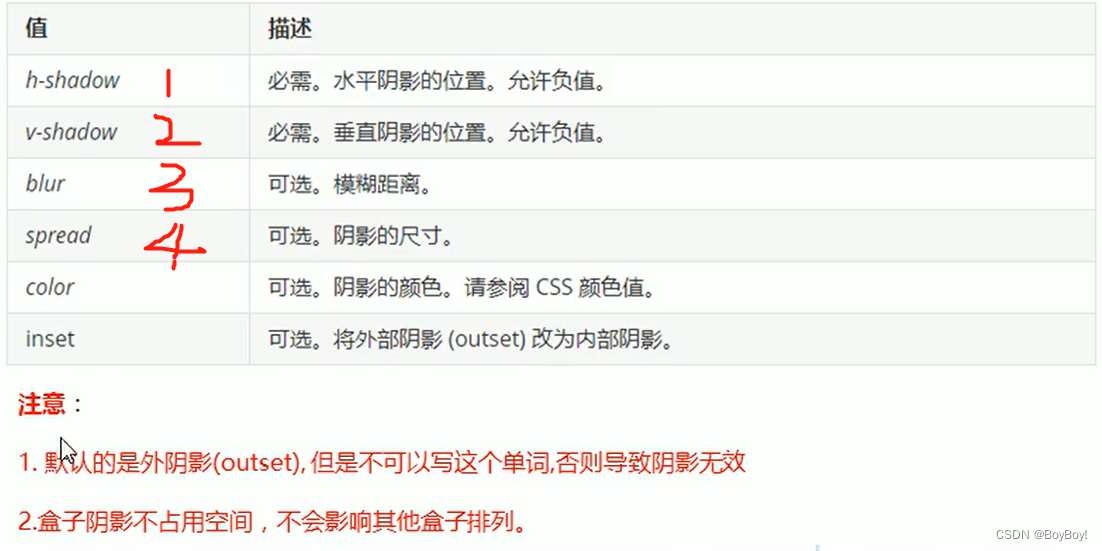
盒子阴影和网页布局
盒子阴影 box-shadow: 10px 10px 10px 4px rgba(0,0,0,.3);//最后一个是透明度 传统网页布局的三种方式 标准流 就是按照规定好的默认方式排列 1.块级元素:div、hr、p、h1~h2、ul、ol、dl、form、table 行内元素会按照书顺序,从左到右顺序排列&#…...

Ph.D,一个Permanent head Damage的群体
一个群体 Permanent head Damage 的博士生群体 Permanent head Damage Ph.D 博士生一年级的同学们,不要担忧或高兴得太早,抱歉你们还没有经历Qualification——预备考试,你们暂且不能被称为博士,只能称自己是要努力成为博士预备…...
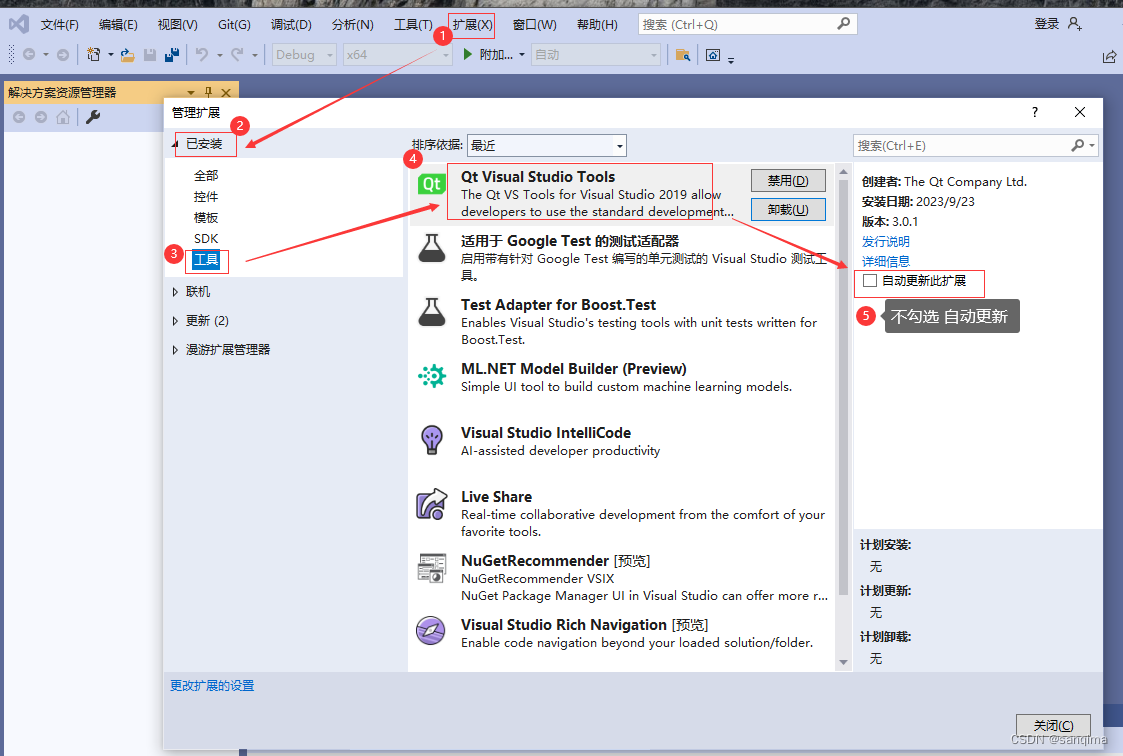
visual studio禁用qt-vsaddin插件更新
visual studio里qt-vsaddin插件默认是自动更新的,由于qt-vsaddin插件新版本的操作方式与老版本相差较大,且新版本不稳定,容易出Bug,所以需要禁用其自动更新,步骤如下: 点击VS2019菜单栏上的【扩展】–…...
Docker通过Dockerfile创建Redis、Nginx--详细过程
创建Nginx镜像 我们先创建一个目录,在目录里创建Dockerfile [rootdocker-3 ~]# mkdir mynginx [rootdocker-3 ~]# cd mynginx [rootdocker-3 ~]# vim Dockerfile Dockerfile的内容 FROM daocloud.io/library/centos:7 RUN buildDepsreadline-devel pcre-devel o…...

关于使用 uniapp Vue3 开发分享页面 语法糖 setup 开发获取ref踩坑
上代码 前端代码 <!-- 分享弹出 --> <uni-popup ref"share" type"share" safeArea backgroundColor"#fff"><uni-popup-share></uni-popup-share> </uni-popup>处理函数 import {onNavigationBarButtonTap} from…...
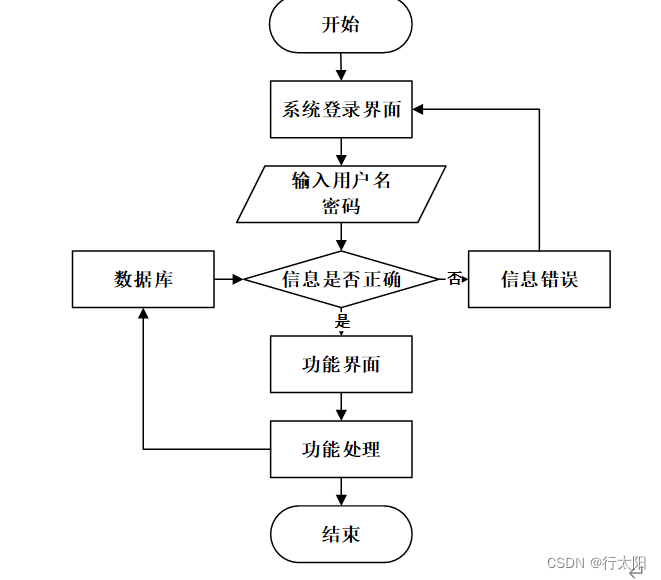
Springboot+vue的时间管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。
演示视频: Springbootvue的时间管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。 项目介绍: 本文设计了一个基于Springbootvue的前后端分离的时间管理系统,采用M(model࿰…...
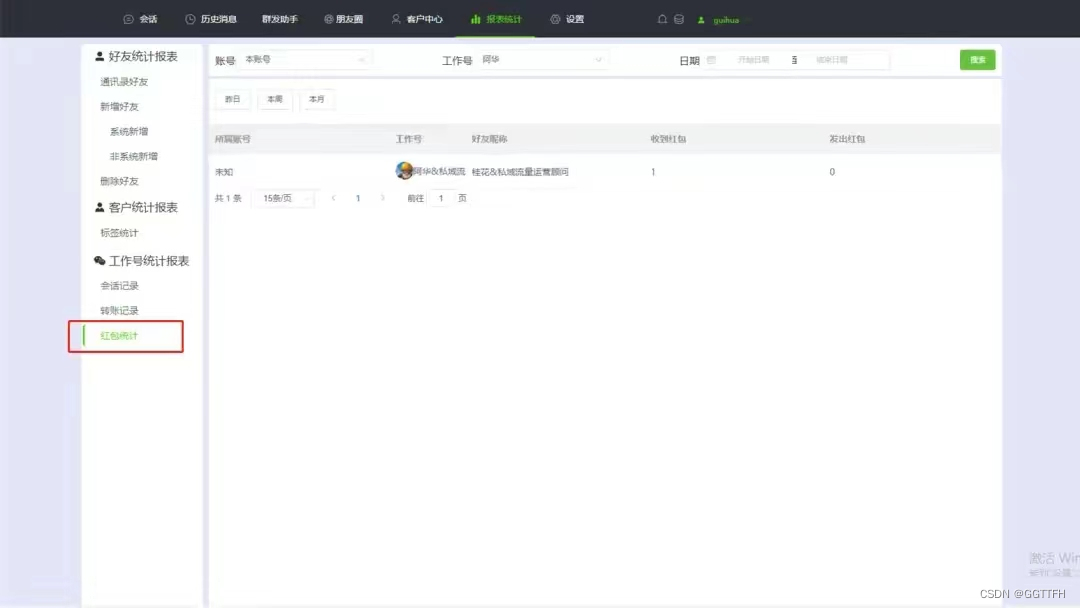
企业如何实时监管员工聊天转账行为
你还在担心员工飞单、私单吗? 你还在担心员工辱骂删除客户吗? 你还在担心员工离职会带走公司客户吗? 你还在担心员工工作不认真,工作量无法统计吗? 。。。。。。。。 在当今互联网时代,企业微信的应用已…...
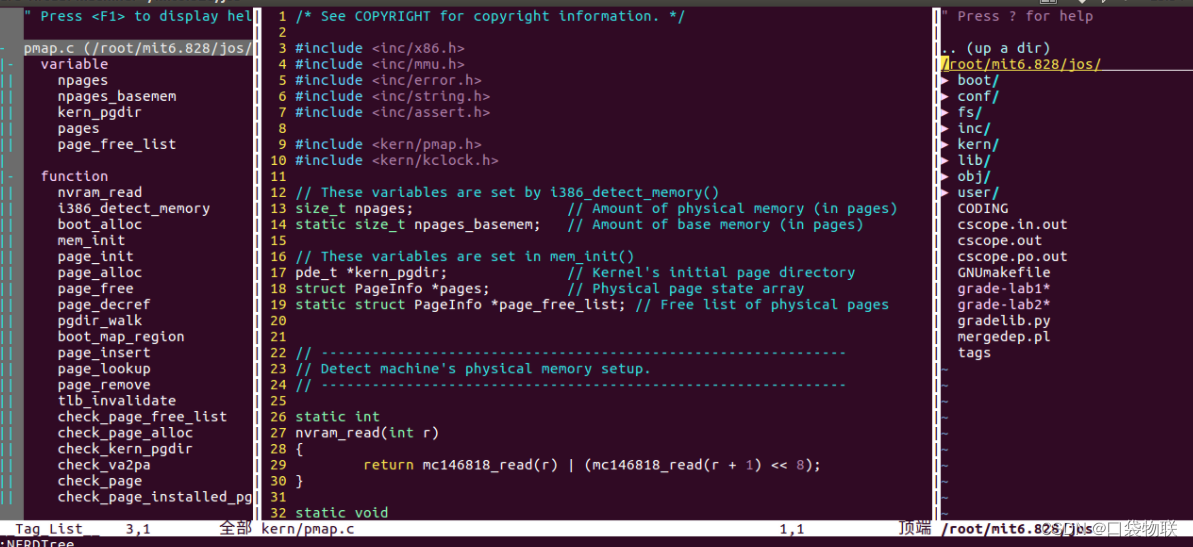
2.2.3.1vim + ctags + cscope + taglist
在window下,我们一般用Source Insight来查看代码而在linux下,使用vim来查看代码,vim是一个简单的文本浏览/编辑器,它可以通过插件的形式,搭建一个完全的类Source Insight环境,通过快捷键的形式,快速查看、定位变量/函数,本文就是基于vim,通过ctags+cscope+taglist+Ner…...

JAVA面经整理(4)
一)Volitaile关键字的作用: 1)保证多线程环境下共享变量的可见性,对于一个线程对于一个共享表变量的修改,其他线程可以立即看到修改之后的共享变量的值 2)可以增加内存屏障来放置多个指令之间的重排序 volatile的使用:常常用于一写多读的情况下ÿ…...

Python3数据科学包系列(一):数据分析实战
Python3中类的高级语法及实战 Python3(基础|高级)语法实战(|多线程|多进程|线程池|进程池技术)|多线程安全问题解决方案 Python3数据科学包系列(一):数据分析实战 Python3数据科学包系列(二):数据分析实战 认识下数据科学中数据处理基础包: (1)NumPy 俗话说: 要学会跑需先…...

【LittleXi】【MIT6.S081-2020Fall】Lab: locks
【MIT6.S081-2020Fall】Lab: locks 【MIT6.S081-2020Fall】Lab: locks内存分配实验内存分配实验准备实验目的1. 举一个例子说明修改前的**kernel/kalloc.c**中如果没有锁会导致哪些进程间竞争(races)问题2. 说明修改前的kernel/kalloc.c中锁竞争contention问题及其后果3. 解释a…...
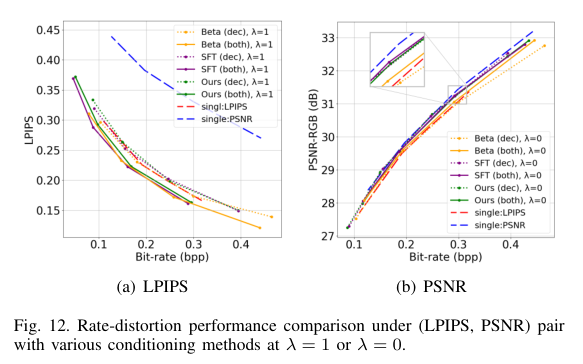
图像压缩:Transformer-based Image Compression with Variable Image Quality Objectives
论文作者:Chia-Hao Kao,Yi-Hsin Chen,Cheng Chien,Wei-Chen Chiu,Wen-Hsiao Peng 作者单位:National Yang Ming Chiao Tung University 论文链接:http://arxiv.org/abs/2309.12717v1 内容简介: 1)方向:…...

C++ 类和对象篇(四) 构造函数
目录 一、概念 1. 构造函数是什么? 2. 为什么C要引入构造函数? 3. 怎么用构造函数? 3.1 创建构造函数 3.2 调用构造函数 二、构造函数的特性 三、构造函数对成员变量初始化 0. 对构造函数和成员变量分类 1. 带参构造函数对成员变量初始化 2. …...

Swing程序设计(5)绝对布局,流布局
文章目录 前言一、布局管理器二、介绍 1.绝对布局2.流布局总结 前言 Swing窗体中,每一个组件都有大小和具体的位置。而在容器中摆放各种组件时,很难判断其组件的具体位置和大小。即一个完整的界面中,往往有多个组件,那么如何将这…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...


