单调队列---数据结构与算法
简介
队列也是一种受限制的线性表和栈相类似,栈是先进后出,而队列是先进先出,就好像一没有底的桶,往里面放东西,如图

在这里也是用数组来实现队列,用数组实现的叫做顺序队列
队列的数组模拟
const int N = 1000010;//在队尾插入元素 队头弹出元素
int q[N],hh,tt=-1; //hh代表队头 tt代表队尾//插入
q[++tt] = x ;//弹出
hh++ ;//判断队列是否为空
if(hh <= tt ) not empty
else empty//取出队头元素
q[hh] ;单调队列
单调队列也就是说其中的元素始终保持单调性
常见应用:找出滑动窗口中的最大值/最小值
如题:给定一个大小为 n ≤ 10^6 的数组。 有一个大小为 k 的滑动窗口,它从数组的最左边移动到最右边。 你只能在窗口中看到 k 个数字。 每次滑动窗口向右移动一个位置。 以下是一个例子: 该数组为 [1 3 -1 -3 5 3 6 7],k 为 3。
输入格式
输入包含两行。
第一行包含两个整数 n 和 k,分别代表数组长度和滑动窗口的长度。
第二行有 n 个整数,代表数组的具体数值。
同行数据之间用空格隔开。
输出格式
输出包含两个。
第一行输出,从左至右,每个位置滑动窗口中的最小值。
第二行输出,从左至右,每个位置滑动窗口中的最大值。
输入样例8 3 1 3 -1 -3 5 3 6 7输出样例
-1 -3 -3 -3 3 3 3 3 5 5 6 7
例子的输出解释:
| 窗口的位置 | 最小值 | 最大值 |
|---|---|---|
| 【1 3 -1】 -3 5 3 6 7 | -1 | 3 |
| 1【 3 -1 -3】 5 3 6 7 | -3 | 3 |
| 1 3 【-1 -3 5 】3 6 7 | -3 | 5 |
| 1 3 -1【 -3 5 3 】6 7 | -3 | 5 |
| 1 3 -1 -3 【5 3 6 】7 | 3 | 6 |
| 1 3 -1 -3 5【 3 6 7】 | 3 | 7 |
对于解开这题我们依旧尝试暴力做法
既然求滑动窗口中的最大值和最小值,那我们只需要让窗口滑动 n - k + 1 次,再每次都对窗口里的k个数,求出最大/小值就可以了,以下是部分代码
//求最小值
for (int i = 0 ; i < n - k + 1 ; i++)
{int min = -1;for (int j = i; j < i + k; j++){if (a[i] <= min){min = a[i];}}printf("%d ", min);
}
//求最大值
//这样的做法不仅要遍历数组一遍,在这个过程中窗口还要遍历,相当于遍历了 n * k 遍,非常浪费时间。
优化的方向也是和之前的单调栈类似,有很多元素根本就不可以在后边用到, 例如
我们求最小值时,当 a [ x ] >= a [ y ] 并且 x > y ,这种情况就可以将 a [ x ] 从我们这个队列删除
反之,易得。
这就得到了队列的单调性
对于这个循环中我们需要做3个步骤
1. 检测队列是否为空 并且 队头是否滑出了窗口,这是什么意思呢?窗口的大小固定是 k ,我们要保证队列中的元素全是窗口里的数的下标,队头保存的下标如果是窗口左边的下标,就说明要将队头的元素移出队列(这里只需要判断一次,因为每次循环最多添加一个元素)
2. 检测队列是否为空 并且队尾所指向的元素是否大于等于此时的元素,如果为真,要将队尾移出队列
3.再将我们此时指向的元素的下标加入队列
4.打印最小值,肯定不是每一次循环都需要打印,你会发现前 k - 1 次不需要打印,变成 i 的话就是i >= k - 1(i从0开始),因为此时窗口都没有满
现在将以上步骤变成代码
#define _CRT_SECURE_NO_WARNINGS 1#include <iostream>using namespace std;const int N = 1000010;
int n, k;
int a[N], q[N]; //q 数组是队列
int hh, tt = -1; //hh是队头 tt是队尾int main(void)
{scanf("%d%d", &n, &k);for (int i = 0; i < n; i++){scanf("%d", &a[i]);}for (int i = 0; i < n; i++){if (hh <= tt && q[hh] < i - k + 1) hh++; // i - k + 1 就是窗口的最左边的下标while (hh <= tt && a[q[tt]] >= a[i]) tt--;q[++tt] = i;if (i >= k - 1 ) printf("%d ", a[q[hh]]);}puts(""); //打印空字符串,虽然打印为空,但是使用 puts() 显示字符串时,系统会自动在其后添加一个换行符hh = 0, tt = -1; //记得要初始化数列for (int i = 0; i < n; i++){if (hh <= tt && q[hh] < i - k + 1) hh++; while (hh <= tt && a[q[tt]] <= a[i]) tt--;q[++tt] = i;if (i >= k - 1) printf("%d ", a[q[hh]]);}puts(""); return 0;
}运行图

成功得到结果
相关文章:

单调队列---数据结构与算法
简介 队列也是一种受限制的线性表和栈相类似,栈是先进后出,而队列是先进先出,就好像一没有底的桶,往里面放东西,如图 在这里也是用数组来实现队列,用数组实现的叫做顺序队列 队列的数组模拟 const int N…...

小程序如何使用自定义组件
使用自定义组件的步骤如下: 创建自定义组件:在小程序项目根目录下的 components 文件夹中创建一个文件夹,然后在该文件夹中创建一个 .json 文件、一个 .wxml 文件和一个 .js 文件,这三个文件分别对应组件的配置、模板和逻辑。 在…...

归并排序含非递归版
目录 1.归并排序的原理 2.实现归并排序 2.1框架 2.2区间问题和后序遍历 2.3归并并拷贝 2.4归并排序代码 2.5测试 3.非递归实现归并排序 3.1初次实现 3.2测试 3.3修改 3.4修改测试 1.归并排序的原理 归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治…...

项目进展(八)-编写代码,驱动ADS1285
一、代码 根据芯片的数据手册编写部分驱动,首先看部分引脚的波形: DRDY: CS: 首先在代码初始化时连续写入三个寄存器: void WriteReg(uint8_t startAddr, uint8_t *regData, uint8_t number) {uint8_t i0;// 循环写number1次…...
【MyBatis-Plus】快速精通Mybatis-plus框架—快速入门
大家在日常开发中应该能发现,单表的CRUD功能代码重复度很高,也没有什么难度。而这部分代码量往往比较大,开发起来比较费时。 因此,目前企业中都会使用一些组件来简化或省略单表的CRUD开发工作。目前在国内使用较多的一个组件就是…...

docker 安装kafka
运行容器 zookeeper: [rootk8s-master ~]# docker run -d --restartalways --log-driver json-file --log-opt max-size100m --log-opt max-file2 --name zookeeper -p 2181:2181 -v /etc/localtime:/etc/localtime zookeeper c603f292813cfd6e2b16fff88a9767cc86fc9bba34d82…...

容器内获得apiserver地址
1.容器的Env的KUBENETES_SERVICE_HOST字段 roottomcat01-69fc8f859b-w9btn:/tmp# env | grep KUBERNETES_SERVICE_HOST10.96.0.1 KUBERNETES_SERVICE_HOST10.96.0.12.通过域名查询 nslookup getent hosts roottomcat01-69fc8f859b-w9btn:/tmp# getent hosts kubernetes.def…...
)
linux服务端c++开发工具介绍(vscode版)
本文适合于有一定c开发经验,但是还不明确如何到linux服务端开发程序的同学。 一、vscode 几年前用的是ssh到云服务上,再用vim在云上开发的形式 ssh dongbeijing.dbj11.158.142.176 vim hello.c 现今,由于vscode比较好用,这几年…...

Linux常用命令大全
Linux常用命令大全 一、文件&目录管理1. 文件和目录操作命令2. 查看文件及内容处理命令3. 文件压缩及解压缩命令4. 搜索文件命令5. 其他 二、Linux 软件包管理三、用户管理1. 用户管理2. 查看系统用户登陆信息的命令 四、进程管理五、网络通信1. 基础网络操作命令2. 深入网…...

Python中取2023, 9, 1——2023, 10, 31的全部时间
使用datetime.date()函数定义了开始和结束日期。然后,我们使用datetime.timedelta()类创建了一个时间范围,其中n表示从开始日期到结束日期之间的天数。最后,我们使用一个for循环迭代时间范围内的日期,并打印每个日期。示例代码演示…...

创建django文件
1、在指定目录里打开终端,输入D:\Softwares\Anaconda3\envs\pytorch\Scripts\django-admin .exe startproject 名称 ,即可在对应目录里创建django文件。...
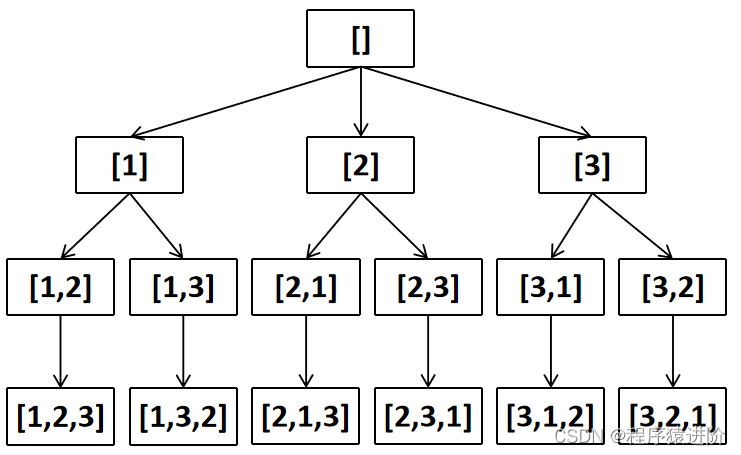
全排列[中等]
优质博文:IT-BLOG-CN 一、题目 给定一个不含重复数字的数组nums,返回其所有可能的全排列。你可以按任意顺序返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 示例…...
mybatise-plus的id过长问题
一、问题情景 笔者在做mp插入数据库(id已设置为自增)操作时,发现新增数据的id过长,结果导致前端JS拿到的数据出现了精度丢失问题,原因是后端id的类型是Long。在网上查了一下,只要在该属性上加上如下注解就可以 TableId(value &q…...
图示矩阵分解
特征值与特征向量 设 A A A 是 n 阶矩阵,如果存在数 λ \lambda λ 和 n 维非零列向量 x x x,满足关系式: A x λ x ( 1 ) Ax \lambda x\quad\quad(1) Axλx(1) 则数 λ \lambda λ 称为矩阵 A A A 的特征值,非零向量 x…...
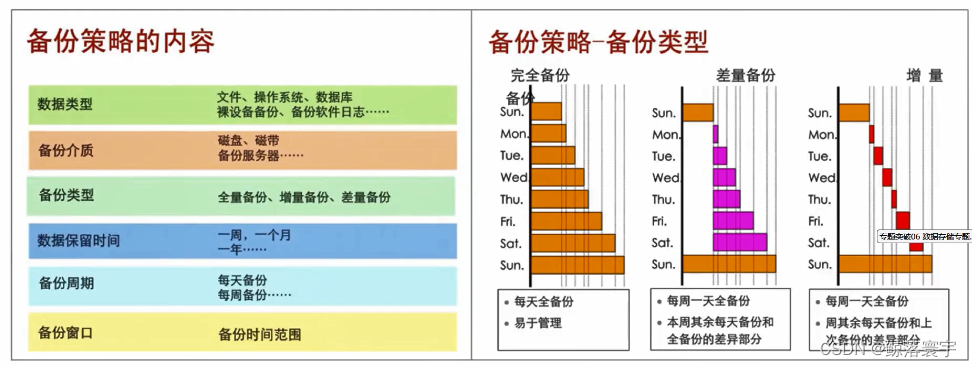
六、互联网技术——数据存储
文章目录 一、存储系统层次结构二、按照重要性分类三、磁盘阵列RAID三、RAID基础四、磁盘阵列分级五、数据备份与恢复六、容灾与灾难恢复 一、存储系统层次结构 常见的三层存储体系结构如下图所示,分为高速缓冲存储器、主存储器和外存储器。 二、按照重要性分类 …...

六、vpp 流表+负载均衡
草稿!!! vpp node其实就是三个部分 1、plugin init 2、set command 3、function 实现功能,比如这里的流表 今天我们再用VPP实现一个流表的功能 一、流表 1.1流表----plugin init VLIB_REGISTER_NODE 注册流表节点 // 注册流…...
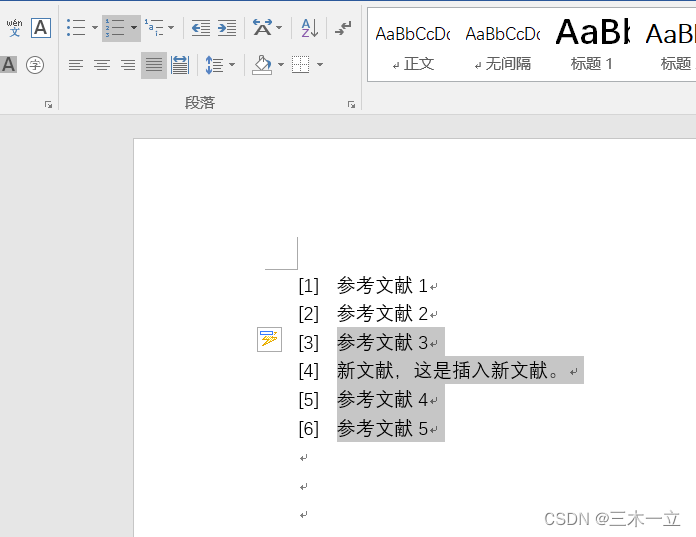
word已排序好的参考文献,插入新的参考文献,序号更新
原排序好的文献序号。 现在在3号后面插入一个新文献。4,5号应该成为5,6 这时在3号后面,回车,就会自动的增长。如下图: 但是如果手滑,把[4]删除了如何排序?? 如下图: …...
二叉树的顺序存储——堆——初识堆排序
前面我们学过可以把完全二叉树存入到顺序表中,然后利用完全二叉树的情缘关系,就可以通过数组下标来联系。 但是并不是把二叉树存入到数组中就是堆了,要看原原来的二叉树是否满足:所有的父都小于等于子,或者所有的父都…...

CYEZ 模拟赛 9
A a ⊥ b ⇒ a − b ⊥ a b (1) a \perp b \Rightarrow a-b \perp ab \tag {1} a⊥b⇒a−b⊥ab(1) 证明: gcd ( a , b ) gcd ( b , a − b ) \gcd(a,b) \gcd(b, a-b) gcd(a,b)gcd(b,a−b),故 a − b ⊥ b a - b \perp b a−b⊥b,同…...
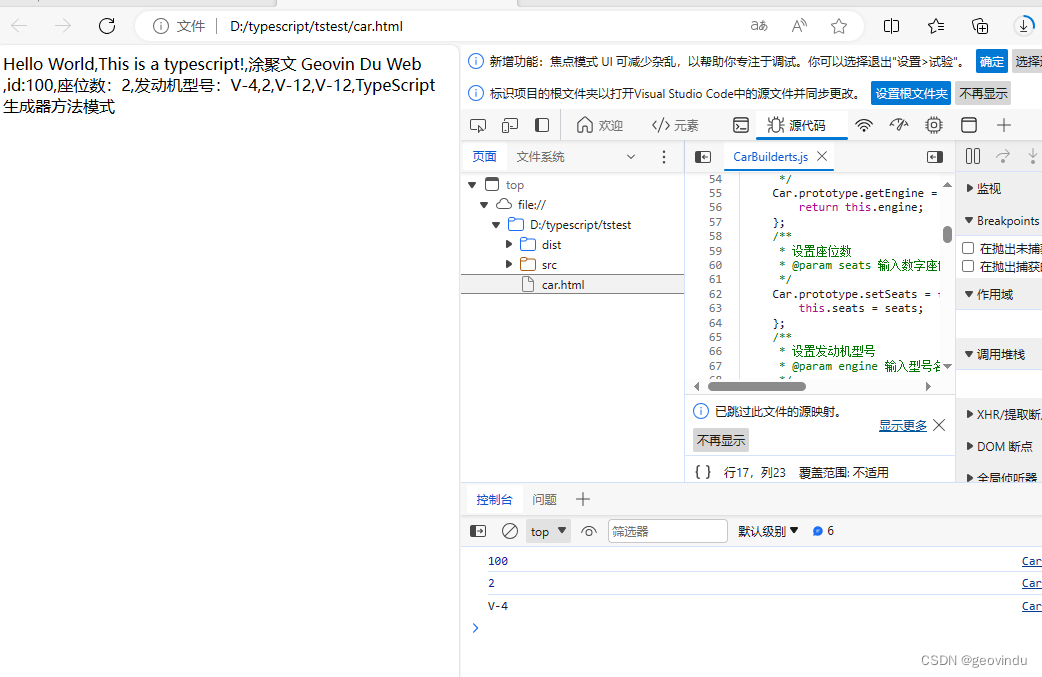
typescript: Builder Pattern
/*** file: CarBuilderts.ts* TypeScript 实体类 Model* Builder Pattern* 生成器是一种创建型设计模式, 使你能够分步骤创建复杂对象。* https://stackoverflow.com/questions/12827266/get-and-set-in-typescript* https://github.com/Microsoft/TypeScript/wiki/…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
