python经典百题之一个素数能被几个9整除
题目:判断一个素数能被几个9整除。
首先,我们需要明确素数的定义:素数是大于1,且只能被1和自身整除的整数。
下面将分别介绍三种实现方法,每种方法附上解题思路、实现代码、以及优缺点。最后,将对这三种方法进行总结,并推荐其中更好的方法。
方法一: 逐步除以9
解题思路:
- 首先判断给定数是否为素数。
- 如果是素数,则从9开始逐步除以9,判断能够整除的次数。
实现代码:
def is_prime(num):if num < 2:return Falsefor i in range(2, int(num ** 0.5) + 1):if num % i == 0:return Falsereturn Truedef count_nines_divisible(num):if not is_prime(num):return 0count = 0while num % 9 == 0:count += 1num //= 9return count# 示例用法
num = 81
divisible_count = count_nines_divisible(num)
print(f"The prime number {num} can be divided by {divisible_count} nines.")
优缺点:
- 优点:
- 直接简单,易于理解和实现。
- 只需要判断能否被9整除,不需要预先生成素数列表。
- 缺点:
- 需要逐步除以9,可能需要多次除法运算。
方法二: 判断因子是否为9
解题思路:
- 首先判断给定数是否为素数。
- 如果是素数,则判断该素数是否只有因子9。
实现代码:
def is_prime(num):if num < 2:return Falsefor i in range(2, int(num ** 0.5) + 1):if num % i == 0:return Falsereturn Truedef is_nines_factor(num):if not is_prime(num):return Falsefactors = [i for i in range(2, num) if num % i == 0]return all(factor == 9 for factor in factors)# 示例用法
num = 81
is_nines = is_nines_factor(num)
print(f"The prime number {num} has all factors as nines: {is_nines}")
优缺点:
- 优点:
- 直接简单,易于理解和实现。
- 只需要判断因子是否为9,不需要预先生成素数列表。
- 缺点:
- 需要判断因子是否为9,可能需要多次判断。
方法三: 利用素数生成算法
解题思路:
- 使用素数生成算法生成素数列表。
- 对于每个素数,判断其能否被9整除。
实现代码:
def generate_primes(limit):primes = []is_prime = [True] * (limit + 1)is_prime[0] = is_prime[1] = Falsep = 2while p * p <= limit:if is_prime[p]:for i in range(p * p, limit + 1, p):is_prime[i] = Falsep += 1for i in range(2, limit + 1):if is_prime[i]:primes.append(i)return primesdef count_nines_divisible(primes):count = 0for prime in primes:if prime % 9 == 0:count += 1return count# 示例用法
limit = 100
primes = generate_primes(limit)
nines_divisible_count = count_nines_divisible(primes)
print(f"Count of primes that can be divided by 9: {nines_divisible_count}")
优缺点:
- 优点:
- 使用素数生成算法生成素数列表,降低了时间复杂度。
- 只需要判断能否被9整除,不需要逐步除以9。
- 缺点:
- 需要实现素数生成算法,稍复杂。
总结与推荐
-
总结:
- 方法一和方法二都是直接简单的实现,但可能需要多次除法运算或多次判断因子,效率不高。
- 方法三利用素数生成算法生成素数列表,避免了逐步除以9或多次判断因子,更高效。
-
推荐:
- 基于素数生成算法的方法(方法三)是相对更好的选择,因为它在时间上进行了较好的优化,并避免了逐步除以9或多次判断因子的操作。生成素数的过程虽然稍复杂,但可以节省时间成本,特别在处理大数字时更为高效。
相关文章:

python经典百题之一个素数能被几个9整除
题目:判断一个素数能被几个9整除。 首先,我们需要明确素数的定义:素数是大于1,且只能被1和自身整除的整数。 下面将分别介绍三种实现方法,每种方法附上解题思路、实现代码、以及优缺点。最后,将对这三种方法进行总结…...

Thymeleaf 内联语法使用教程
1 表达式内联 Thymeleaf标准方言允许使用标签属性(th:)来实现很多的功能,但在有些场景之下,需要将表达式直接写入HTML 代码中和CSS代码中及JavaScript代码中【代码和html文件在一起,分能不开,待验证,有验证的朋友可…...

Django学习笔记-实现聊天系统
笔记内容转载自 AcWing 的 Django 框架课讲义,课程链接:AcWing Django 框架课。 CONTENTS 1. 实现聊天系统前端界面2. 实现后端同步函数 1. 实现聊天系统前端界面 聊天系统整体可以分为两部分:输入框与历史记录。 我们需要先修改一下之前代…...
C++转换函数
什么是转换函数? C转换函数是一种特殊的成员函数,用于将一个类的对象转换为另一个类型。它是通过在类中定义特定的函数来实现的。 转换函数的用途: 类型转换:转换函数可以将一个类的对象从一种类型转换为另一种类型。这样可以方便地在不同…...

Spring Boot中的@Controller使用教程
一 Controller使用方法,如下所示: Controller是SpringBoot里最基本的组件,他的作用是把用户提交来的请求通过对URL的匹配,分配个不同的接收器,再进行处理,然后向用户返回结果。下面通过本文给大家介绍Spr…...
【17】c++设计模式——>原型模式
原型模式的定义 c中的原型模式(Prototype Pattern)是一种创建型设计模式,其目的是通过复制(克隆)已有对象来创建新的对象,而不需要显示的使用构造函数创建对象,原型模式适用于创建复杂对象时&a…...

金三银四好像消失了,IT行业何时复苏!
文章目录 1. 宏观经济形势2. 技术发展趋势3. 教育与培训4. 远程工作和自由职业5. 行业需求和公司招聘计划结论 🎉欢迎来到Java面试技巧专栏~金三银四好像消失了,IT行业何时复苏! ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页&…...
PDF文件超出上传大小?三分钟学会PDF压缩
PDF作为一种流行的文档格式,被广泛用于各种场合,然而有时候PDF文件的大小超出了上传限制,这时候我们就需要采取一些措施来减小PDF文件的大小,下面就给大家分享几个方法,一起来学习下吧~ 方法一:嗨格式压缩大…...

java入坑之国际化编程
一、字符编码 1.1概述 字符编码 --字符:0,a,我,①,,… --计算机只用0和1,1bit(0或者1) --ASCIL码(American Standard Code for Information Interchange) 美国信息交换标准代码,奠定计算机编码基础用一个字节(1Byte8b…...
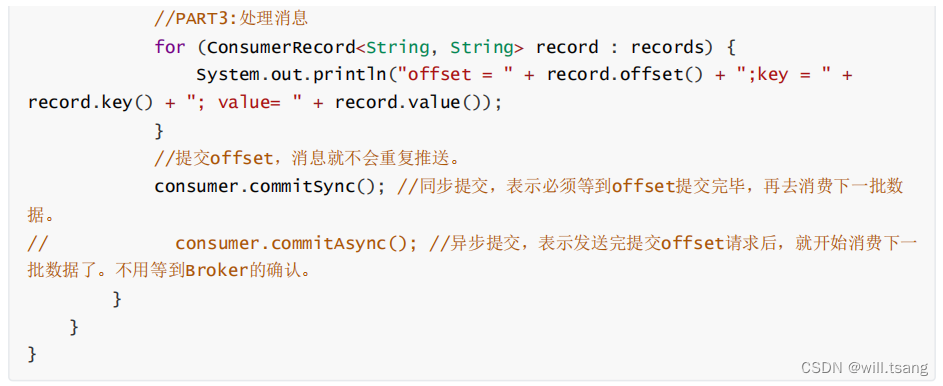
Kafka客户端核心参数详解
这一部分主要是从客户端使用的角度来理解 Kakfa 的重要机制。重点依然是要建立自己脑海中的 Kafka 消费模型。Kafka 的 HighLevel API 使用是非常简单的,所以梳理模型时也要尽量简单化,主线清晰,细节慢慢扩展。 一、从基础的客户端说起 Kaf…...
踩大坑ssh免密登录详细讲解
目 录 问题背景 环境说明 免密登录流程说明 1.首先要在对应的用户主机名的情况下生成密钥对,在A服务器执行 2.将A服务器d公钥拷贝到B服务器对应的位置 3.在A服务器访问B服务器 免密登录流程 0.用户说明 1.目前现状演示 2.删除B服务器.ssh 文件夹下面的…...
操作系统八股
1、请你介绍一下死锁,产生的必要条件,产生的原因,怎么预防死锁 1、死锁 两个或两个以上的进程在执行过程中,因争夺共享资源而造成的一种互相等待的现象,若无外力作用,它们都将无法推进下去。此时称系统处…...

Hudi SQL DDL
本文介绍Hudi在 Spark 和 Flink 中使用SQL创建和更改表的支持。 1.Spark SQL 创建hudi表 1.1 创建非分区表 使用标准CREATE TABLE语法创建表,该语法支持分区和传递表属性。 CREATE TABLE [IF NOT EXISTS] [db_name.]table_name[(col_name data_type [COMMENT col_co…...
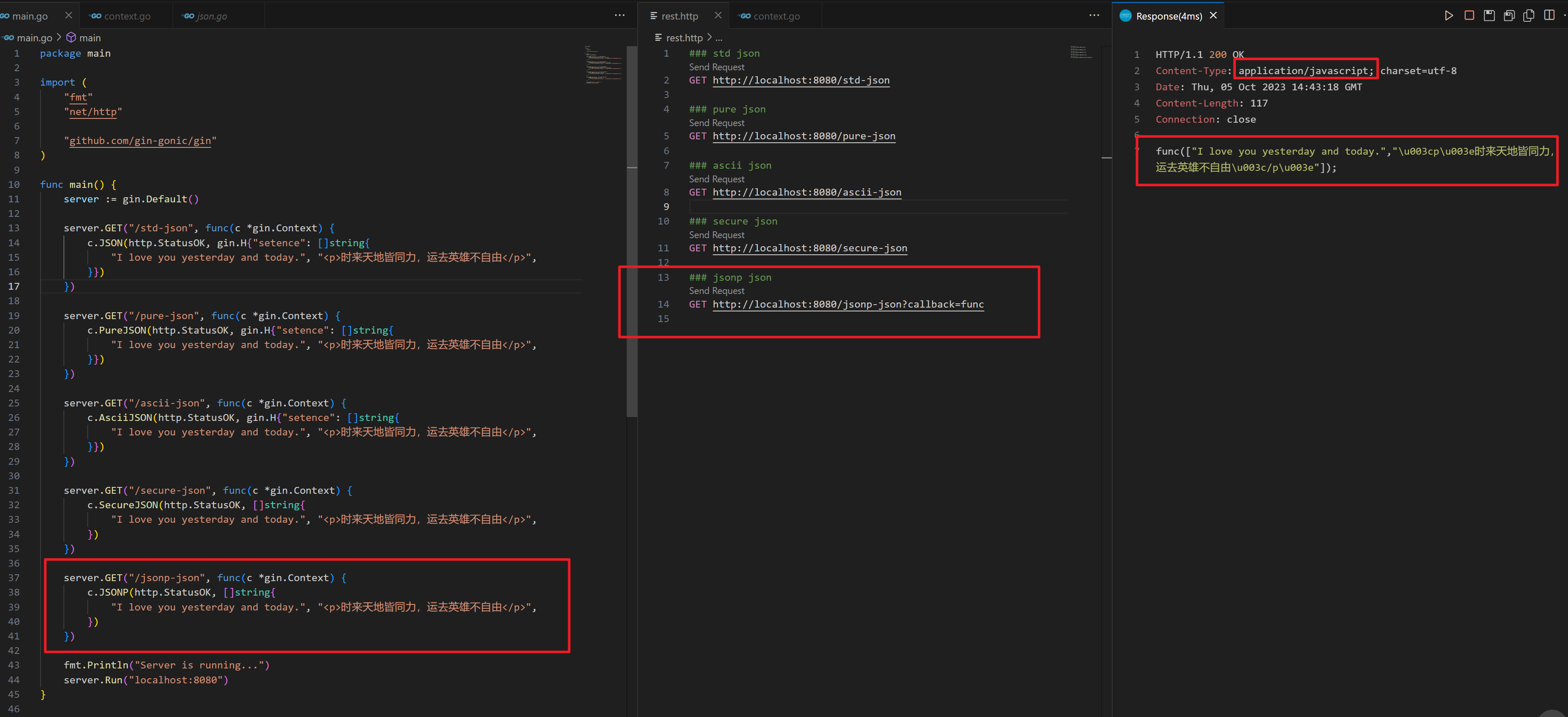
gin 框架的 JSON Render
gin 框架的 JSON Render gin 框架默认提供了很多的渲染器,开箱即用,非常方便,特别是开发 Restful 接口。不过它提供了好多种不同的 JSON Render,那么它们的区别是什么呢? // JSON contains the given interface obje…...
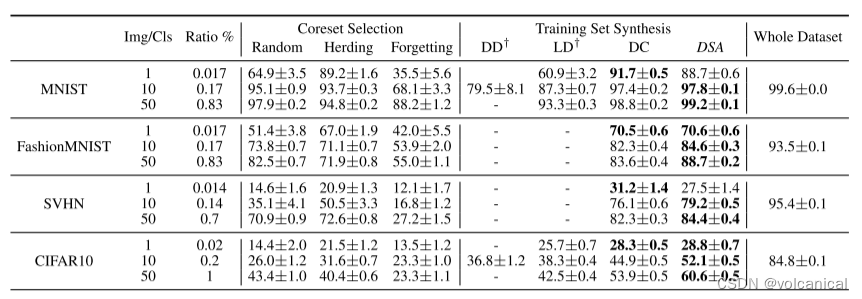
《Dataset Condensation with Differentiable Siamese Augmentation》
《Dataset Condensation with Differentiable Siamese Augmentation》 在本文中,我们专注于将大型训练集压缩成显著较小的合成集,这些合成集可以用于从头开始训练深度神经网络,性能下降最小。受最近的训练集合成方法的启发,我们提…...
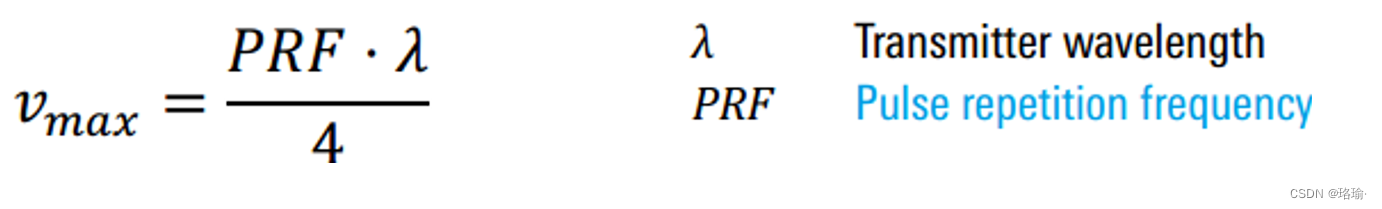
多普勒频率相关内容介绍
图1 多普勒效应 1、径向速度 径向速度是作用于雷达或远离雷达的速度的一部分。 图2 不同的速度 2、喷气发动机调制 JEM是涡轮机的压缩机叶片的旋转的多普勒频率。 3、多普勒困境 最大无模糊范围需要尽可能低的PRF; 最大无模糊速度需要尽可能高的PRF;…...
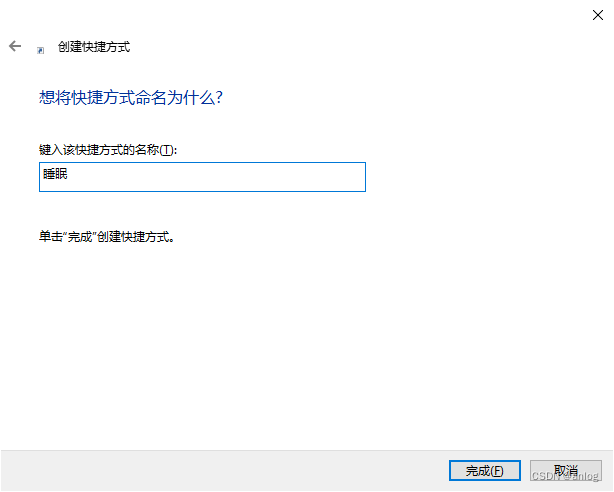
win10睡眠快捷方式
新建快捷方式 如下图 内容如下 rundll32.exe powrprof.dll,SetSuspendState 0,1,0 下一步 点击完成即可。 特此记录 anlog 2023年10月6日...

C++中的static和extern关键字
1 声明和定义 声明就是告诉编译器有这个东西的存在,而定义则是这个东西的实现。 对于变量来说,声明就是告诉编译器存在这个名称的变量,定义则是给这个变量分配内存并赋值: // 变量声明,声明时不能赋值,如…...

JAVA经典百题之找完数
题目:一个数如果恰好等于它的因子之和,这个数就称为"完数"。例如61+2+3.编程找出1000以内的所有完数。 程序分析 首先,我们需要编写一个程序来找出1000以内的所有完数。"完数"是指一个数等于它的…...

CSS 滚动驱动动画 view-timeline-inset
view-timeline-inset 语法例子🌰 正 scroll-padding 为正正的 length正的 percentage 负 scroll-padding 为负负的 length负的 percentage 兼容性 view-timeline-inset 在使用 view() 时说过, 元素在滚动容器的可见性推动了 view progress timeline 的进展. 默认…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...
