深度剖析数据在内存中的存储(下)(适合初学者)
上篇讲解了整形在内存中的存储方式,这篇文章就来继续讲解浮点数在内存中的存储方式。
上篇地址:
(5条消息) 深度剖析数据在内存中的存储(上)_陈大大陈的博客-CSDN博客
目录:
3.浮点型在内存中的存储
3.1.浮点数的范围以及精度
3.2.一个例子
3.3.浮点数存储规则
3.4.解释前面的题目
话不多说,咱们开始!
3.浮点型在内存中的存储
常见的浮点数:
3.1415926
2a13
浮点数家族包括: float、double、long double 类型。
浮点数表示的范围:float.h中定义
3.1.浮点数的范围以及精度
我们可以使用一个叫做everything的软件来查找我们需要的文件,当然没有也没事,只是不太方便
软件链接:voidtools
打开everything输入float.h。
然后将float.h拖入vs编译器。
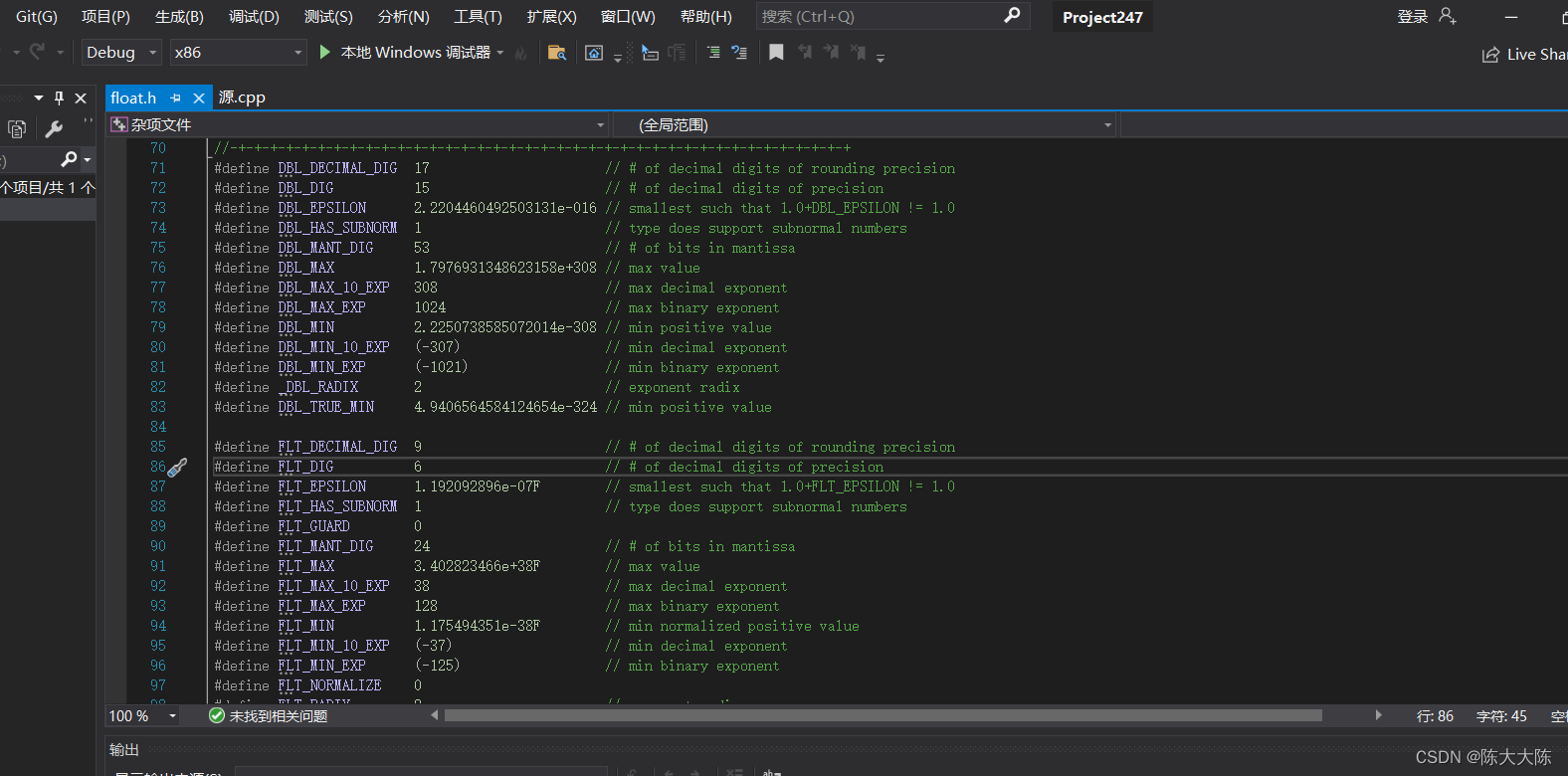 我们可以在里面清楚地看到浮点数类型的最大值,最小值和精度。
我们可以在里面清楚地看到浮点数类型的最大值,最小值和精度。
其中:
DBL_EPSILON 表示double类型的精度。
DBL_MIN 表示double类型的最小值。
DBL_MAX表示double类型的最大值。
比葫芦画瓢。
FLT_EPSILON,FLT_MAX,FLT_MIN则是float类型的数据。
而整形类型的存储范围则可以去limits.h里面来找。
将其拖入编译器,可以看到整形数据的各项定义。
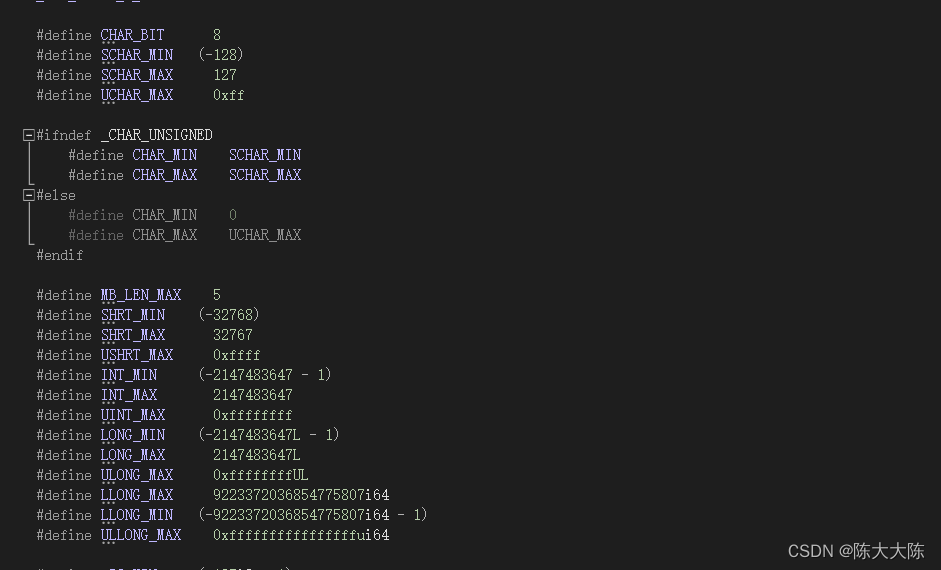
其中, SCHAR表示signed char,UCHAR表示unsigned char。
SHRT表示 short,USHRT表示unsigned short。
LLONG 表示long long,ULLONG表示unsigned long long。
3.2.一个例子
接下来就是重头戏了。大家先来看一道小题。
#define _CRT_SECURE_NO_WARNING
#include<stdio.h>
int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);*pFloat = 9.0;printf("num的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);return 0;
}输出的结果是什么呢?
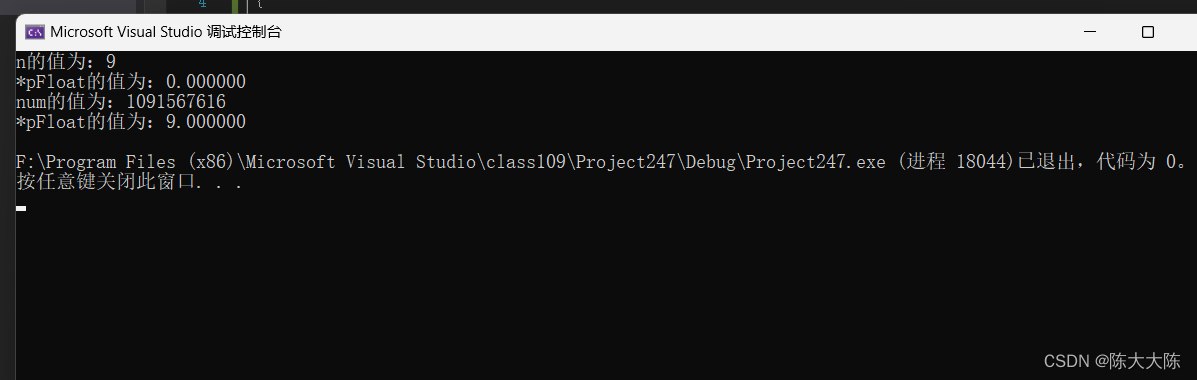
打印出的数字和我们预想的不太一样,我们以为 printf("*pFloat的值为:%f\n",*pFloat);所打印出来的值应该是9.000000,可结果确实0。当 *pFloat为浮点数时,我们
这说明浮点型和整形在内存中的读取方式是不一样的。
3.3.浮点数存储规则
num 和 *pFloat 在内存中明明是同一个数,为什么浮点数和整数的解读结果会差别这么大?
要理解这个结果,一定要搞懂浮点数在计算机内部的表示方法。
详细解读:
根据国际标准IEEE(电气和电子工程协会) 754,任意一个二进制浮点数V可以表示成下面的形式:
(-1)^S * M * 2^E
(-1)^S表示符号位,当S=0,V为正数;当S=1,V为负数。
M表示有效数字,大于等于1,小于2。 2^E表示指数位
举例来说: 十进制的5.0,写成二进制是 101.0 ,相当于 1.01×2^2 。
那么,按照上面V的格式,可以得出S=0,M=1.01,E=2。
十进制的-5.0,写成二进制是 -101.0 ,相当于 -1.01×2^2 。
那么,S=1,M=1.01,E=2。 IEEE 754规定: 对于32位的浮点数,最高的1位是符号位s,接着的8位是指数E,剩下的23位为有效数字M。
(IEEE 754全称IEEE二进制浮点数算术标准,详细解释在下面链接,我就不赘述了)
IEEE 754_百度百科 (baidu.com)
32位的浮点数,第一位(最高位)是符号位S,紧接的8位是指数位E,最后的23位是尾数位M。
而64位的浮点数,第一位是符号位S,下面的11位是指数位E,最后的52位是尾数位M。
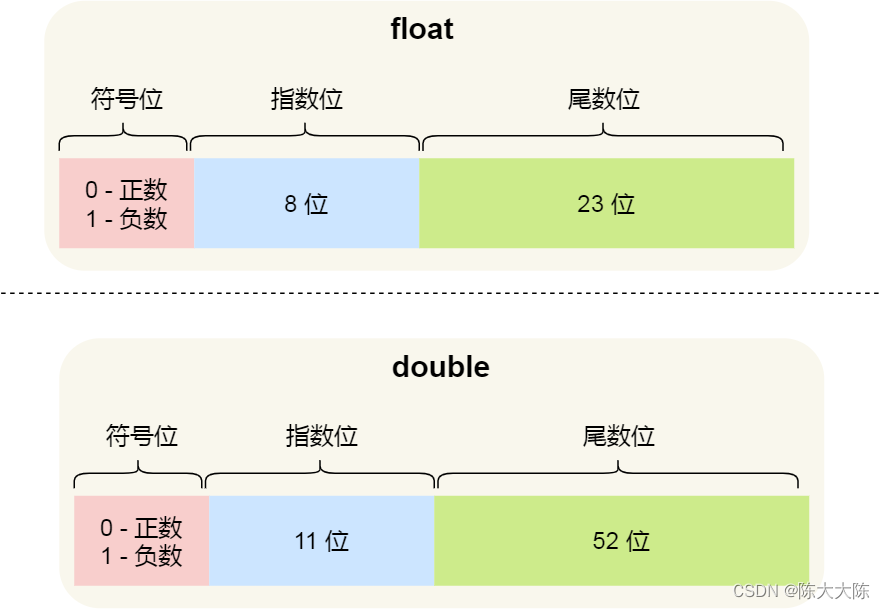
IEEE 754对有效数字M和指数E,还有一些特别规定。
前面说过, 1≤M<2 ,也就是说,M可以写成 1.xxxxxx 的形式,其中xxxxxx表示小数部分。
IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的 xxxxxx部分。
比如保存1.01的时 候,只保存01,等到读取的时候,再把第一位的1加上去。
这样做的目的,是节省1位有效数字。以32位浮点数为例,留给M只有23位, 将第一位的1舍去以后,等于可以保存24位有效数字。
至于指数E,情况就比较复杂。
首先,E为一个无符号整数(unsigned int)
这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0~2047。
但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数 是127;对于11位的E,这个中间数是1023。
比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即 10001001。
然后,指数E从内存中取出还可以再分成三种情况:
E不全为0或不全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将 有效数字M前加上第一位的1。
比如:
0.5(1/2)的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为 1.0*2^(-1),其阶码为-1+127=126,表示为 01111110,而尾数1.0去掉整数部分为0,补齐0到23位00000000000000000000000,则其二进制表示形式为:
0 1111110 00000000000000000000000
E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值。
有效数字M不再加上第一位的1,而是还原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字。
E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s)
3.4.解释前面的题目
#define _CRT_SECURE_NO_WARNING
#include<stdio.h>
int main()
{int n = 9;float* pFloat = (float*)&n;printf("n的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);*pFloat = 9.0;printf("num的值为:%d\n", n);printf("*pFloat的值为:%f\n", *pFloat);return 0;
}为什么 0x00000009 还原成浮点数,就成了 0.000000?
将0x00000009拆分。
得到下面的结果。
0000 0000 0000 0000 0000 0000 0000 0000 1001
第一位符号位s=0,后面8位的指数 E=00000000 , 最后23位的有效数字M=000 0000 0000 0000 0000 1001。
带入上面所讲的浮点数存储公式,为:
(-1)^0*0.00000000000000000000000*2^(-126)
这样的数字小到我们无法用数字来写出来,所以用十进制小数表示就是0.000000。
再看例题的第二部分。
请问浮点数9.0,如何用二进制表示?还原成十进制又是多少?
我们知道,9.0用二进制来表示即为1001.0,也即1.001*2^3
可以看出来,符号位S为0,指数位E为3+127=130,也即10000010,尾数位M为1.001。
二进制形式如下。
0 10000010 001 0000 0000 0000 0000 0000
这个32位的二进制数用10进制来计算,结果就是1091567616。
数据在内存中存储终于完结了!谢谢大家的观看。如果文章有错误,请各位不吝赐教。
可以的话,不妨给小陈点个小小的赞鼓励一下。
咱们下期再见!

相关文章:

深度剖析数据在内存中的存储(下)(适合初学者)
上篇讲解了整形在内存中的存储方式,这篇文章就来继续讲解浮点数在内存中的存储方式。 上篇地址: (5条消息) 深度剖析数据在内存中的存储(上)_陈大大陈的博客-CSDN博客 目录: 3.浮点型在内存中的存储 3.1.浮点数的…...
智慧物联网系统源码:一个用于数据的收集、处理、可视化、设备管理、设备预警、报警的平台
项目简介: 一个用于数据的收集、处理、可视化、设备管理、设备预警、报警的平台,通过平台将所有设备连接起来,为上层应用提供设备的管理、数据收集、远程控制等核心物联网功能。 支持支持远程对设备进行实时监控、故障排查、远程控制&#…...

2023年,拥有软考证书在这些地区可以领取福利补贴
众所周知,软考的含金量很高,比如可以入户、领取技能补贴、抵扣个税、以考代评、招投标加分,入专家库… 今天小编给大家收集了拥有软考证书可以领取软考福利的地区,希望对大家有所帮助! 【深圳】 入户 ①核准类入户:…...

使用Unity在材质球上实现绘画:详细解释每一行Shader代码!
在Unity中实现在材质球上绘画可以使用下面这个步骤:创建一个基础的材质球:在Unity的项目面板中创建一个新材质球,然后将其分配给您要绘画的对象。创建一个Shader:为了实现在材质球上绘画,您需要使用一种特殊的Shader。…...

Tesseract 4.0训练字库并且识别训练后的图片
各个工具下载链接在文章底部! 重要!!自己先创建一个空文件夹(名字随意),用来保存训练后的模型 ,还需要在里面创建一个 名称为tessdata 的文件夹 ,必须叫这个名 可以先使用下载后的进行测试训练(只需要把ja…...

ChatGPT热潮背后,金融行业大模型应用路在何方?——金融行业大模型应用探索
ChatGPT近两个月以来不断引爆热点,对人工智能应用发展的热潮前所未有地高涨,ChatGPT所代表的大模型在语义理解、多轮交互、内容生成中所展现的突出能力令人惊喜。而人工智能技术在金融行业的落地应用仍然面临挑战,虽然已经让大量宝贵的人力从…...

【怎么预防sql注入,以及还有预防其他的什么网络攻击】
SQL注入是一种常见的Web攻击,通过在Web应用程序中注入恶意SQL语句来获取或修改数据库中的数据。为了防止SQL注入,开发者可以采取以下措施: 1、使用参数化查询(Prepared Statement)或存储过程(Stored Proce…...

2023年全国最新机动车签字授权人精选真题及答案4
百分百题库提供机动车签字授权人考试试题、机动车签字授权人考试预测题、机动车签字授权人考试真题、机动车签字授权人证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 11.使用转化炉原理测量氮氧化物的排气分析仪进行排气污…...
【Java】用记事本实现“HelloWorld”输出
【在进行以下操作前需要下载好JDK并配置好对应的环境变量】 一、在任意文件夹中创建一个新的文本文档文件并写入以下代码 public class Hello{public static void main (String[] args){System.out.print("Hello,World!");} } 二、修改文件名称及文件类型为 Hello.j…...

我希望早点知道的关于成长的建议
人上了年纪,往往在诸如更加闭塞,更加固执这些缺点之外,再多出来一个缺点:那就是动不动就爱给别人建议。我当然也未能免俗。有时候会听到同样悲观且固执的过来人告诉我,这些建议说了和没说效果都一样,人们在…...

【哈希表】使用方法总结
1. uthash简介开源的第三方头文件,这只是一个头文件:uthash.h。uthash还包括三个额外的头文件,主要提供链表,动态数组和字符串。utlist.h为C结构提供了链接列表宏。utarray.h使用宏实现动态数组。utstring.h实现基本的动态字符串。…...

【笑小枫-面试篇】Java基础面试题整理,努力做全网最全
写在前面 或许你只是想白嫖内容,或许你也会忽略这段文字,但我还是想弱弱的说 题目整理耗费了大量精力,希望可以给博主点赞收藏,谢谢大家啦 我呢,笑小枫,一个努力的普通人,也希望可以花1秒钟记住…...
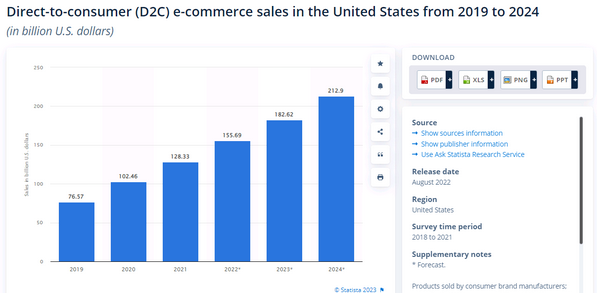
亚马逊短期疲软,但长期前景乐观
来源:猛兽财经 作者:猛兽财经 由于投资者对亚马逊(AMZN)前景的担忧,导致该公司的股价在过去一年中下跌了39%。然而猛兽财经认为亚马逊近期面临的不利因素只是暂时的,该公司还是有充分的条件可以在医疗保健和物流领域获得重大增长机…...

webgis高德地图
webgis高德地图 首先准备工作,注册一个高德地图账号,然后在创建一个新应用生一个key跟appId 高德开放平台 接着创建一个html页面 高德配置手册 <style>* {margin: 0;padding: 0;}#...
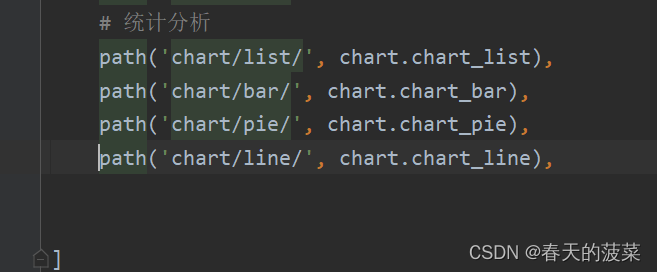
django项目实战十(django+bootstrap实现增删改查)进阶数据统计
目录 一、echarts 1、下载 2、配置 二、实现统计分析页面--架构和柱图 1、url 2、chart.py 3、chart_list.html 4、修改url 5、新增chart_bar方法 6、修改chart_list.html 四、饼图 1、url 2、视图chart.py新增 3、修改chart_list.html 五、折线图 1、url 2、char…...
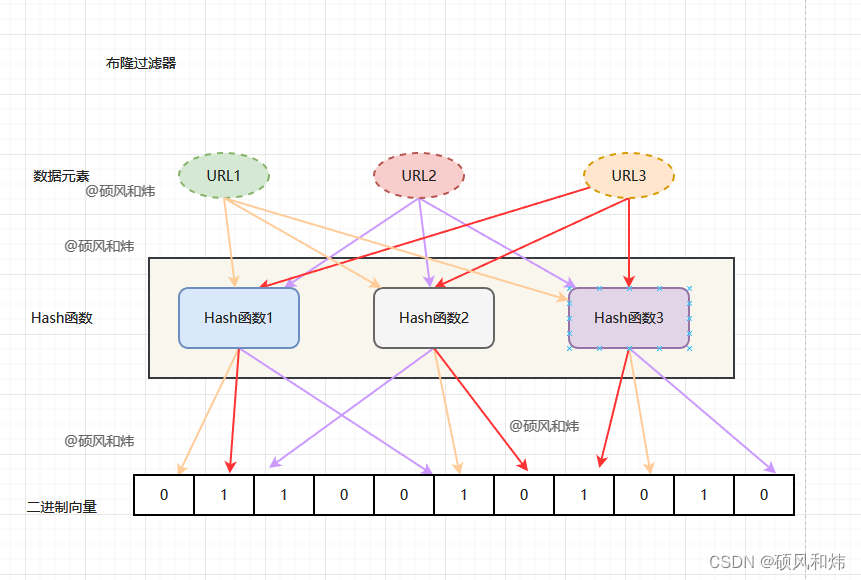
【布隆过滤器(Bloom Filter)基本概念与原理、Bloom Filter优点与缺点、以及应用场景】
布隆过滤器(Bloom Filter)基本概念与原理、Bloom Filter优点与缺点、以及应用场景 Bloom Filter 基本概念 布隆过滤器是1970年由一个叫布隆的小伙子提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在…...

unity的Rendertexture上面显示粒子特效最便捷的解决方案
一、为什么不显示 1.为什么粒子特效也不显示? 不显示是正常的,因为当前为背景的点设置为A为0时已经被剔除,当前位置粒子特效的颜色也会被剔除。 因为clip发生在融合blend之前,blend发生在所有颜色输出之后的帧缓存。 2.为什么NGUI的Unlit/Premultiplied Colored的shade…...

Docker 查询、停止、删除和重启容器
docker 列出所有容器IDdocker ps -aq[rootlocalhost conf]# docker ps -aq f81aa5f48427 06a66409d7ce 1c3d38b948ba 62233dfad35b 4b0032878886 0f6f368c4c1d 7d98a59a8012 1906ba6bfbe1 [rootlocalhost conf]#docker 查看所有运行容器docker ps -a[rootlocalhost conf]# dock…...
)
面试历程(3)
1、HashMap为什么要使用红黑树,不能使用平衡二叉树(AVL树) 二叉查找树具有的特性: 左子树上所有结点的值均小于或等于它的根结点的值。右子树上所有结点的值均大于或等于它的根结点的值。左、右子树也分别为二叉排序树。AVL树是严格平衡二叉树(左右两个子树的高度差的绝对…...
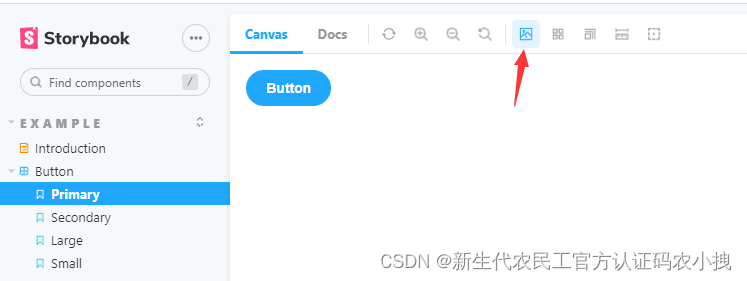
【storybook】你需要一款能在独立环境下开发组件并生成可视化控件文档的框架吗?(二)
storybook回顾继续说说用法配置文件介绍回顾 上篇博客地址: https://blog.csdn.net/tuzi007a/article/details/129192502说了部分用法。 继续说说用法 配置文件介绍 开发环境的配置都在.storybook目录中,里面包含了2个文件 main.js preview.js先看m…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

云原生安全实战:API网关Envoy的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关 作为微服务架构的统一入口,负责路由转发、安全控制、流量管理等核心功能。 2. Envoy 由Lyft开源的高性能云原生…...
