课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
一、内容介绍
该测量系统基于三轴加速度和三轴陀螺仪,安装在钻柱内部,随钻柱一起旋转,形成捷联惯性导航系统,安装如下图所示:
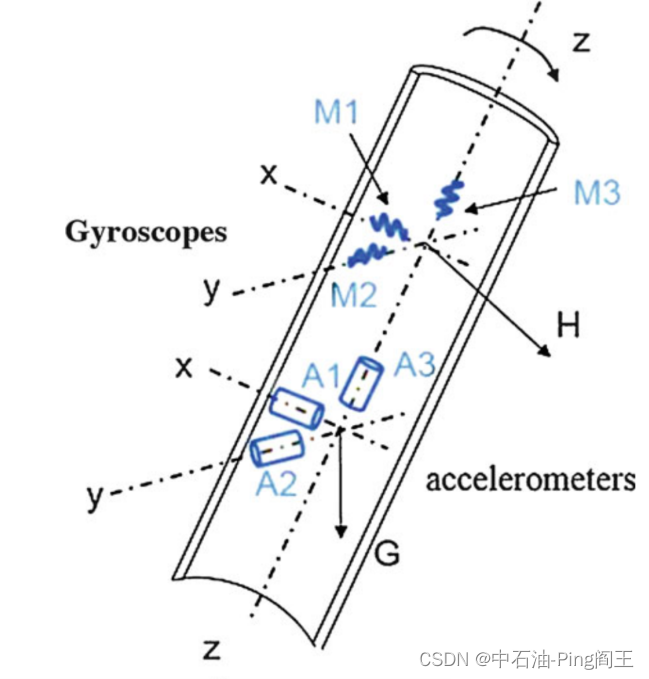
假设三轴加速度和陀螺仪的输出为: f b = [ f x f y f z ] T f^b=\begin{bmatrix}f_{x} & f_{y} &f_{z} \end{bmatrix}^T fb=[fxfyfz]T w b = [ w x w y w z ] T w^b=\begin{bmatrix}w_{x} & w_{y} &w_{z} \end{bmatrix}^T wb=[wxwywz]T
使用这六轴的输出可以非常有效的求解姿态,应用惯性导航的求解算法,可以实现钻孔时的连续测量。加速度计和陀螺仪可以在坐标系中提供线加速度和角速度。但是,如果要求解钻具的位姿,则需要将该坐标系转换为另一个坐标系。
Xe、Ye、Ze三个轴代表地球坐标系。导航坐标系用于计算载体的位置、速度和姿态,因为导航坐标系沿当地的北、东、垂直方向,如下图中的“N, E, UP”,其中λ为经度角,φ为纬度角。在载体坐标系下,利用INS力学方程可得到井斜、井向和工具面角。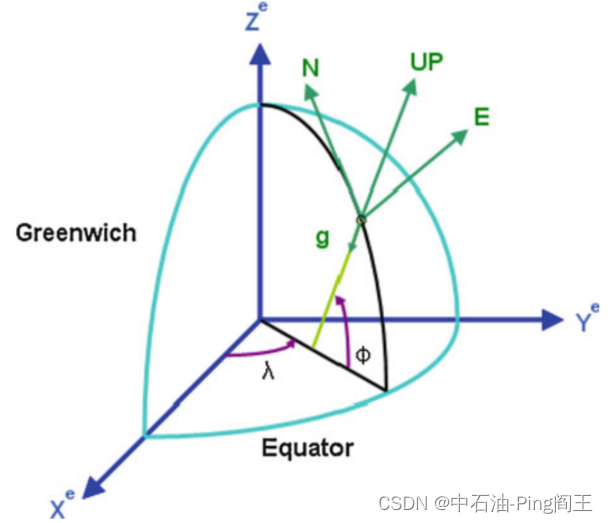
将b系统中测得的加速度和角速度值通过变换矩阵Rn b转换为n系统,即可求解井底工具的空间位置和姿态[28]。定义底部的经度为λ,纬度为φ,海拔为h,则其位置可表示为: r n = [ φ λ h ] T r^n=\begin{bmatrix}φ & λ &h \end{bmatrix}^T rn=[φλh]T
定义n系统的速度分量,向北速度为Vn,向东速度为Ve,垂直速度为Vu。然后定义n系统的速度为: r n = [ V e V n V u ] T r^n=\begin{bmatrix}V^e & V^n &V^u\end{bmatrix}^T rn=[VeVnVu]T
速度分量可以表示为位置分量对时间的导数:
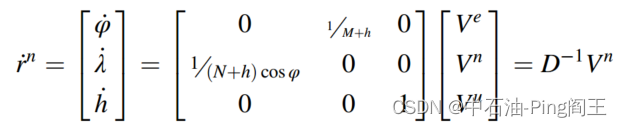
上式中,M为子午线的曲率半径,N为地球椭圆的曲率半径。
在载体坐标系下,加速度计 f b = [ f x f y f z ] T f^b=\begin{bmatrix}f_{x} & f_{y} &f_{z}\end{bmatrix}^T fb=[fxfyfz]T 通过变换矩阵 R b n R^n_{b} Rbn转换到地理坐标系的测量值为:

n坐标系中的加速度分量 f n f^n fn可以对速度分量 v n v^n vn积分。但由于地球本身的存在,会影响求解过程。地球自转速度为 w e = 15 d e g / h r w^e=15deg/hr we=15deg/hr,用n坐标系表示的角速度矢量如下式所示:
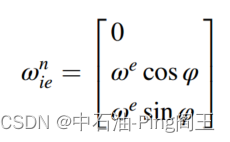
地理坐标系的变化取决于导航坐标系中北方和垂直方向的定义。北方方向通常指向子午线方向,垂直方向指向地球表面,如下图所示: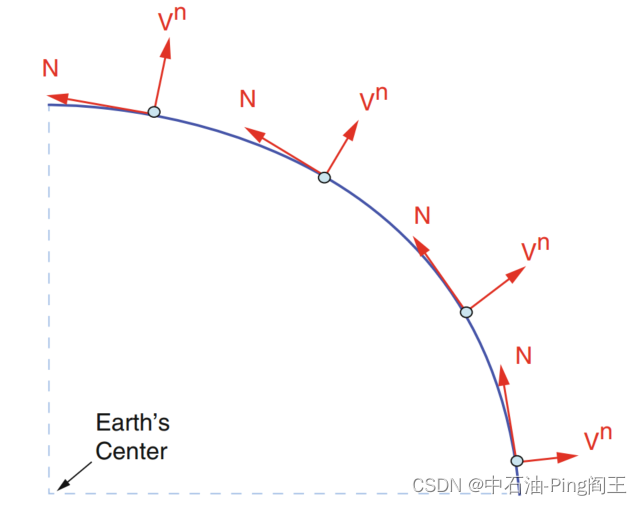
在导航坐标系中,角速度矢量可表示为:
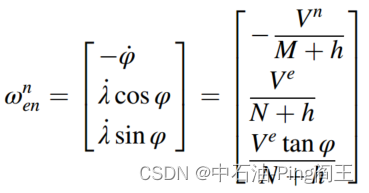
地球引力也影响IMU的加速度测量。我们可以用重力模型来修正。地球重力场可以表示为: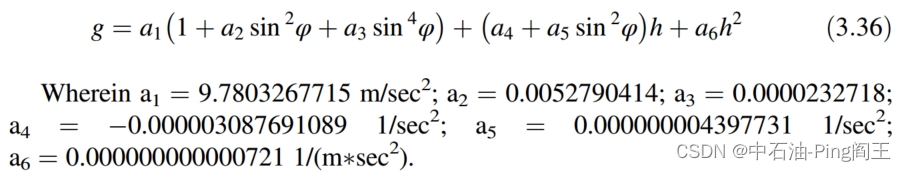
地球引力场在n系列中可以表示为: g n = [ 0 0 − g ] g^n=\begin{bmatrix}0&0&-g\end{bmatrix} gn=[00−g].考虑到地球因素的影响,速度分量Vn的变化率可以表示为: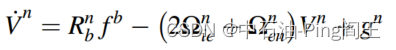
其中:
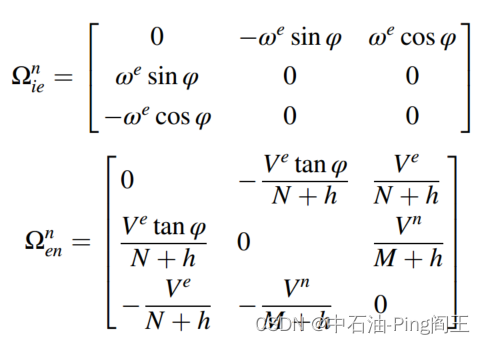
变换矩阵 R b n R^n_{b} Rbn可由以下微分方程得到:
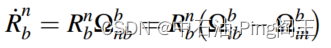
其中 Ω i b b Ω^b_{ib} Ωibb为陀螺仪测得的角速度的反对称矩阵,角速度矢量 Ω i b b Ω^b_{ib} Ωibb可表示为:
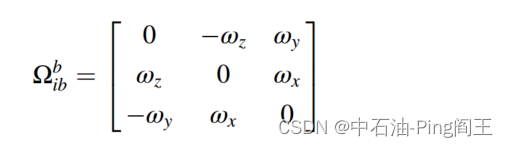
陀螺仪测量底部钻具的角速度,同时也测量地球自转的角速度和导航坐标系的方向。因此,需要从 Ω i b b Ω^b_{ib} Ωibb中减去角速度 Ω i n b Ω^b_{in} Ωinb,以消除这两个因素的影响。角速度矢量 Ω i n b Ω^b_{in} Ωinb包含两部分,第一部分是地球自转速度 Ω i e b Ω^b_{ie} Ωieb和导航坐标系方向变化速度 Ω e n b Ω^b_{en} Ωenb,如下图所示: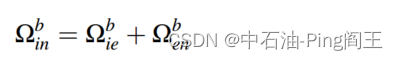
速度矩阵的反对称矩阵可以表示为: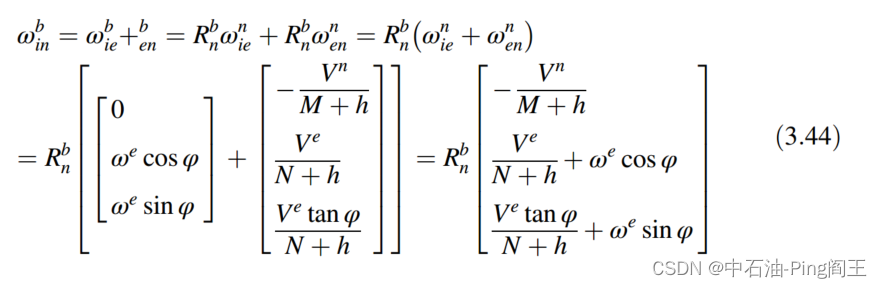
最后得到变换矩阵如下: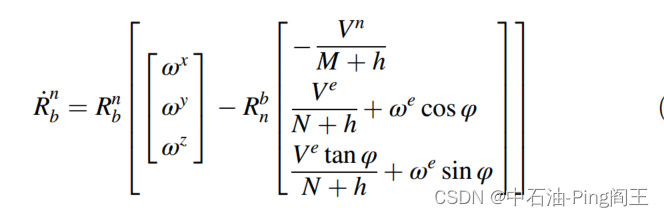
定义井斜角为θ,方位角为ψ,工具面为φ,变换矩阵 R b n R^n_{b} Rbn可表示为: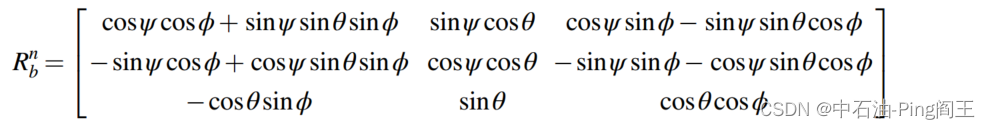
根据前面的假设,三轴加速度计的输出信号为: f b = [ f x f y f z ] T f^b=\begin{bmatrix}f_{x} & f_{y} &f_{z} \end{bmatrix}^T fb=[fxfyfz]T 三轴陀螺仪的输出信号为: w b = [ w x w y w z ] T w^b=\begin{bmatrix}w_{x} & w_{y} &w_{z} \end{bmatrix}^T wb=[wxwywz]T 从测量的角速度可以计算出角度变化量:

同样,由加速度的测量值可以计算出线速度: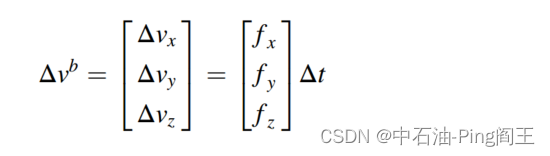
考虑到地球自转和导航坐标系方向变化的影响,在时刻tk时,角度的增加可表示为: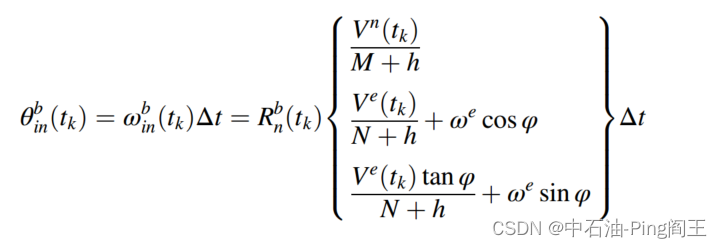
然后,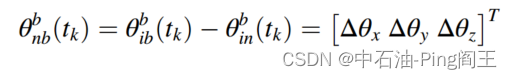
综上所述,基于地理坐标系的捷联惯性导航系统的力学方程如下:
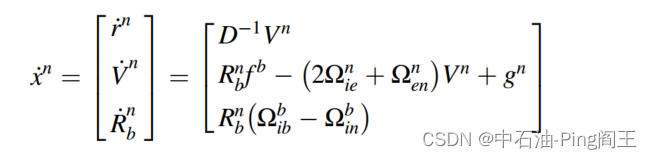
上式的解可以用欧拉角法、方向余弦法或四元数法求解。通过在载体轴上安装三轴加速度计和三轴陀螺仪,可以通过测量值获得载体的姿态、速度和位置等信息。
二、往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
相关文章:
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
一、内容介绍 该测量系统基于三轴加速度和三轴陀螺仪,安装在钻柱内部,随钻柱一起旋转,形成捷联惯性导航系统,安装如下图所示: 假设三轴加速度和陀螺仪的输出为: f b [ f x f y f z ] T f^b\begin{bmatrix}f_{x} …...

1876. 长度为三且各字符不同的子字符串
1876. 长度为三且各字符不同的子字符串 C代码:滑动窗口 // 存在三种字符,且不重复、子串数量 int countGoodSubstrings(char * s){int k 3;int hash[26] {0};int len 0;int l 0;int ans 0;for (int i 0; i < strlen(s); i) {hash[s[i] - a];if…...
Mall脚手架总结(一)——SpringSecurity实现鉴权认证
前言 在结束理论知识的学习后,荔枝开始项目学习,这个系列文章将围绕荔枝学习mall项目过程中总结的知识点来梳理。本篇文章主要涉及如何整合Spring Security和JWT实现鉴权认证的功能!希望能帮助到一起学习mall项目的小伙伴~~~ 文章目录 前言 …...
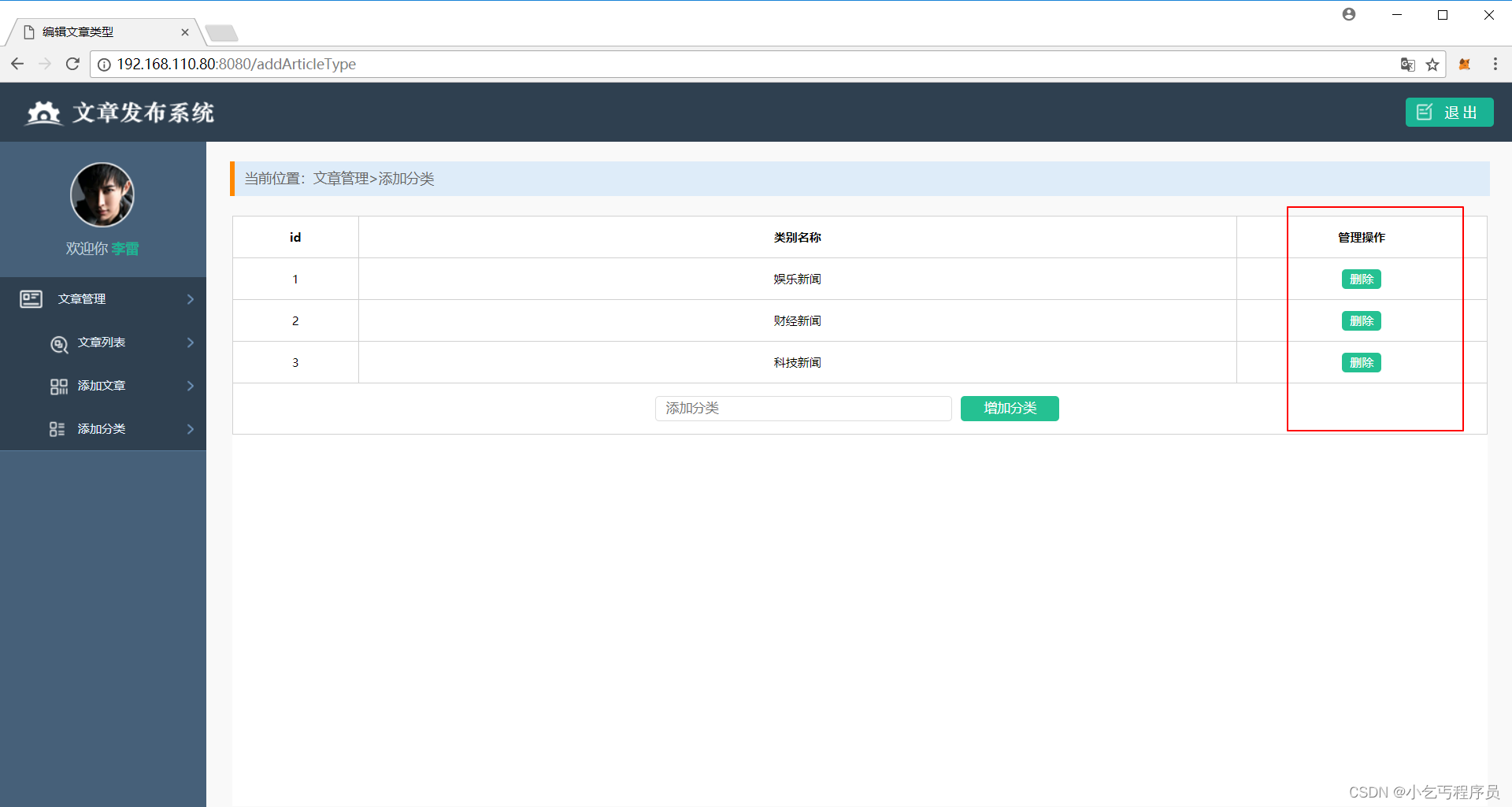
beego-简单项目写法--路径已经放进去了
Beego案例-新闻发布系统 1.注册 后台代码和昨天案例代码一致。,所以这里面只写一个注册的业务流程图。 **业务流程图 ** 2.登陆 业务流程图 登陆和注册业务和我们昨天登陆和注册基本一样,所以就不再重复写这个代码 但是我们遇到的问题是如何做代码的迁移&…...

Linux-CPU相关常用命令合集
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、cpu相关常用命令 二、cpuinfo 参数详细对照表 前言 本篇文章主要记录平时Linux-常用命令整理! 提示:以下是本篇文章正文内容&#…...
vue 百度地图/天地图设置铺满屏幕100%,解决空隙问题
设置100%无效,刷新依然右侧有空隙,解决:min-width: 100vw; <div class"aui-flex-col" style"width: 100%; height:100%"><div id"mapAllCon" style"width: 100%; min-width: 100vw; height: 10…...
)
第五章:最新版零基础学习 PYTHON 教程—Python 字符串操作指南(第六节 - Python 中字符串的逻辑运算符)
对于 python 中的字符串,布尔运算符(and、or、not)起作用。让我们考虑两个字符串,即 str1 和 str2,并在它们上尝试布尔运算符: Python3 str1 = str2 = geeks# 使用 repr 打印带引号的字符串# 返回 str1 print(repr(str1 and str2)) # 返回 str1 print(repr(str2 and…...
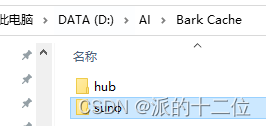
Bark Ai 文本转语音 模型缓存位置修改
默认缓存位置在:~/.cache 加入环境变量:XDG_CACHE_HOME,指定缓存位置 修改后新的位置为: D:\Ai\Bark\Bark Cache...
Docker 镜像的创建
目录 一、Docker镜像的创建 1、基于已有镜像创建 2、基于本地模板创建 3、基于dockerfile创建 3.1 dockerfile结构 3.2 构建镜像命令 二、镜像分层的原理 1、联合文件系统(UnionFS) 2、镜像加载的原理 三、Dockerfile 操作常用的指令 案例实验…...
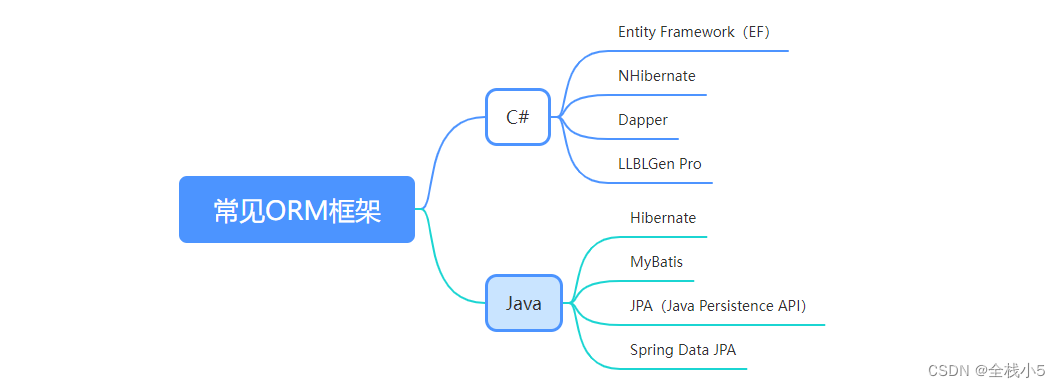
【ORM】浅聊C#和Java的ORM底层框架
给自己一个目标,然后坚持一段时间,总会有收获和感悟! 国庆假期马上结束,闲暇时间,突然对Ado.Net这个词的由来感兴趣,然后就一顿复习了一遍,顺便也了解了下java关于ORM框架的底层是什么ÿ…...
windows redis 自启动 Redis服务无法启动报错1067问题
如果你的系统服务里面已经有redis服务并且无法启动,则使用下面的命令卸载此服务 ! 1、停止Redis服务: redis-server --service-uninstall 2、删除系统服务 sc delete redis 进入到你的Redis安装目录,我的在以下目录,谨记此时不…...

Ubuntu Server CLI专业提示
基础 网络 获取所有接口的IP地址 networkctl status 显示主机的所有IP地址 hostname -I 启用/禁用接口 ip link set <interface> up ip link set <interface> down 显示路线 ip route 将使用哪条路线到达主机 ip route get <IP> 安全 显示已登录的用户 w…...

Centos7升级OpenSSH9.1
最近遇到了服务器漏洞,需要对服务器的OpenSSH版本进行升级,查阅了相关资料,总结出了一套比较简单的方案。中间遇到的个别问题也进行了记录,供大家参考。 下载准备 从https://ftp.jaist.ac.jp/pub/OpenBSD/OpenSSH/portable/opens…...
linux——信号
目录 一.信号的保存 二.信号集操作 1.信号集 2.信号集操作函数 3.sigprocmask 4.sigpending 三. 信号的捕捉 1.内核态和用户态 2. sigaction 四.可重入函数 五.SIGCHLD信号 一.信号的保存 实际执行信号的处理动作称为信号递达(Delivery)。信号从产生到递达之间的状…...
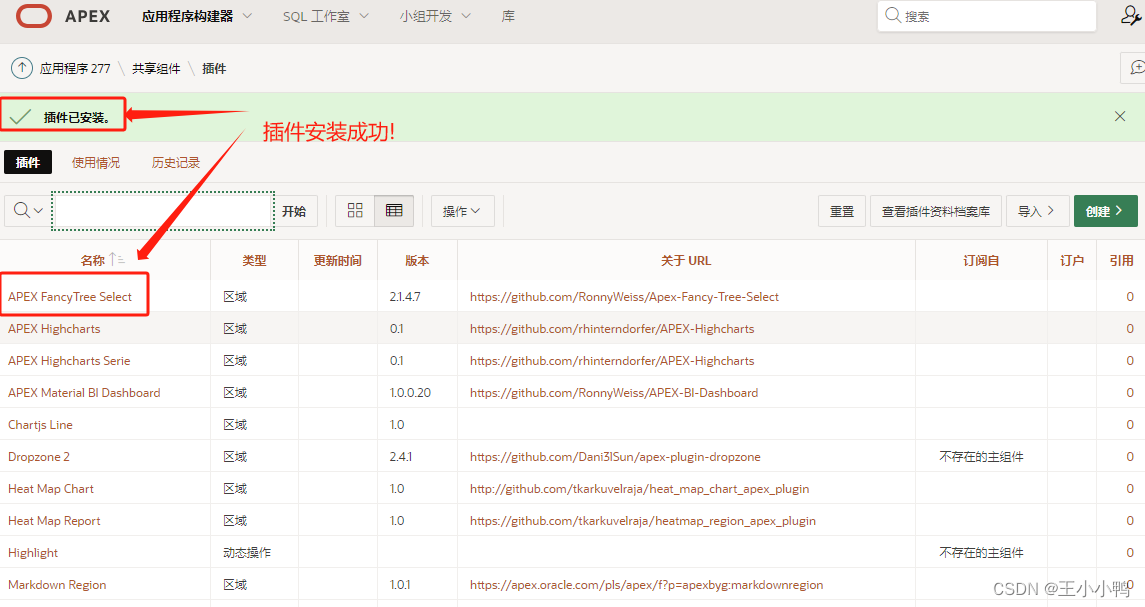
存档&改造【03】Apex-Fancy-Tree-Select花式树的导入及学习
Apex-Fancy-Tree-Select git学习网页 GitHub - RonnyWeiss/Apex-Fancy-Tree-Select: Fancy Tree Plug-in for Oracle APEX 如何从其他应用程序导出已有插件到新应用程序中 1.从其他应用程序导出插件 其他应用程序-【共享组件】-【插件】-【任务 导出插件】-选择想要导出的…...

【单片机】14-I2C通信之EEPROM
1.EEPROM概念 1.EEPROM 1.1 一些概念 (1)一些概念:ROM【只读存储器---硬盘】,RAM【随机访问存储器--内存】,PROM【可编程的ROM】,EPROM【可擦除ROM】,EEPROM【电可擦除ROM】 1.2 为什么需要EE…...
Mini-dashboard 和meilisearch配合使用
下载的meilisearch一般是development模式,内置客户端,修改客户端后需要重要全部编译,花时间太长了。前后端分离才是正道,客户端修改不用重新编译后端。 方法如下: 1、修改配置文件/etc/meilisearch.toml,…...

leetcode 886. 可能的二分法
给定一组 n 人(编号为 1, 2, …, n), 我们想把每个人分进任意大小的两组。每个人都可能不喜欢其他人,那么他们不应该属于同一组。 给定整数 n 和数组 dislikes ,其中 dislikes[i] [ai, bi] ,表示不允许将…...
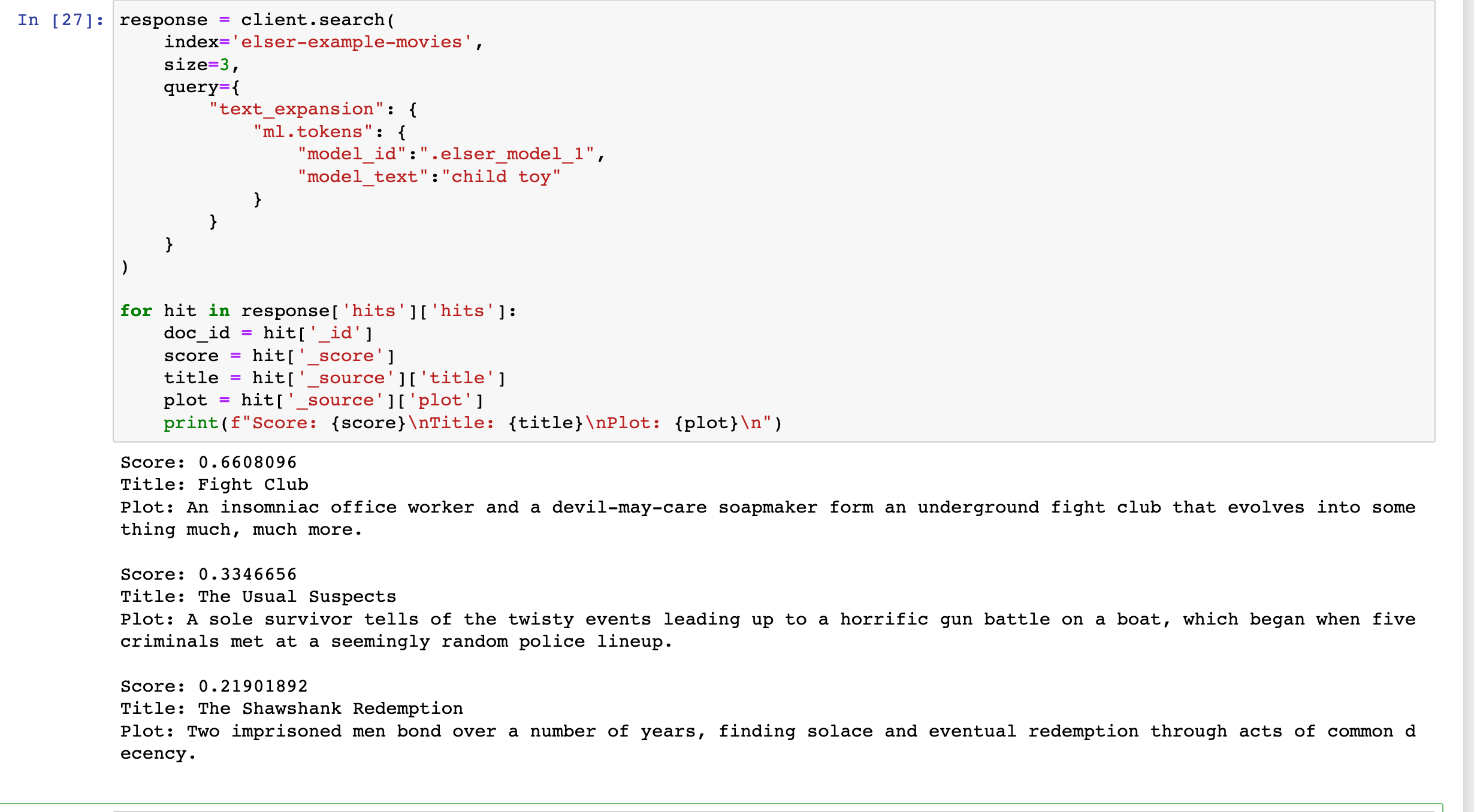
Elasticsearch:使用 ELSER 文本扩展进行语义搜索
在今天的文章里,我来详细地介绍如何使用 ELSER 进行文本扩展驱动的语义搜索。 安装 Elasticsearch 及 Kibana 如果你还没有安装好自己的 Elasticsearch 及 Kibana,请参考如下的链接来进行安装: 如何在 Linux,MacOS 及 Windows 上…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

