数学建模:最优化问题及其求解概述
数学建模:最优化问题及其求解概述
- 最优化问题
- 定义
- 分类
- 离散优化问题
- 连续优化问题
- 求解
此博客围绕运筹学以及最优化理论的相关知识,通俗易懂地介绍了最优化问题的定义、分类以及求解算法。
最优化问题
定义
数学优化(Mathematical Optimization)问题,也叫最优化问题,属于运筹学研究的主要内容,它是指在一定约束条件下,求解一个目标函数的最大值(或最小值)问题。这种问题在生活中很常见,例如如何利用有限的资源,实现最大的收益。下面给出最优化问题的数学定义:
给定一个函数 f f f,寻找一个变量 x 0 ∈ D x_0 \in D x0∈D,使得对于 D D D中所有的 x x x, f ( x 0 ) ≤ f ( x ) f(x_0) \leq f(x) f(x0)≤f(x)(最小化)或者 f ( x 0 ) ≥ f ( x ) f(x_0) \geq f(x) f(x0)≥f(x)(最大化)。函数 f f f被称为目标函数或代价函数,通常集合 D D D需要满足一定的约束, D D D中的元素被称为可行解,一个最小化(或者最大化)目标函数的可行解被称为最优解。
分类
根据变量 x x x 的定义域是否为实数域,数学优化问题可以分为离散优化问题和连续优化问题。
离散优化问题
离散优化(Discrete Optimization)问题是目标函数的输入变量为离散变量,比如为整数或有限集合中的元素。离散优化问题的求解一般都比较困难,优化算法的复杂度都比较高。离散优化问题主要有两个分支:
- 组合优化(Combinatorial Optimization):其目标是从一个有限集合中找出使得目标函数最优的元素。在一般的组合优化问题中,集合中的元素之间存在一定的关联,可以表示为图结构。典型的组合优化问题有旅行商问题(TSP,又称最短路径问题)、背包问题(Knapsack Problem,KP)、最小费用最大流(Minimum Cost Maximum Flow,MCMF)等。很多机器学习问题都是组合优化问题,比如特征选择、聚类问题、超参数优化问题以及结构化学习(Structured Learning)中标签预测问题等。通常小规模的组合优化问题可以采用精确求解算法进行最优解的计算,而大规模的组合优化问题一般采用启发式算法进行求解。
- 整数规划(Integer Programming):输入变量为整数。一般常见的整数规划问题为整数线性规划(Integer Linear Programming,ILP)。整数线性规划的一种最直接的求解方法是:(1)去掉输入必须为整数的限制,将原问题转换为一般的线性规划问题,这个线性规划问题为原问题的松弛问题;(2)求得相应松弛问题的解;(3)把松弛问题的解四舍五入到最接近的整数。但是这种方法得到的解一般都不是最优的,因此原问题的最优解不一定在松弛问题最优解的附近,但可能可以为问题求解提供一个较好的可行解,因为这种方法得到的解也不一定满足约束条件。所以常用小规模整数规划问题的求解方法是采用精确求解算法;而对于大规模的整数规划问题一般采用启发式算法求解,虽然启发式算法不能求得整数规划的最优解,但是却能在短时间(通常多项式时间)内给出一个较好的可行解。
连续优化问题
连续优化(Continuous Optimization)问题是目标函数的输入变量为连续变量。在连续优化问题中,根据是否有变量的约束条件,可以将此类优化问题分为无约束优化问题和约束优化问题:
- 无约束优化问题(Unconstrained Optimization)中变量 x 无任何约束,其可行域为整个实数域。针对连续优化中的无约束问题,通常的求解方法时梯度下降法,例如随机梯度下降算法、带动量的随机梯度下降算法和Adam算法等等。
- 约束优化问题(Constrained Optimization)中变量 x 需要满足一些等式或不等式的约束。约束优化问题最经典的算法是使用拉格朗日乘数法来进行求解。这种方法将一个有 n 个变量与 k 个约束条件的最优化问题转换为一个有 ( n + k ) 个变量的方程组的极值问题,其变量不受任何约束。
此外,根据目标函数和约束条件是否线性,可以将此类优化问题分为线性优化问题和非线性优化问题:
- 如果目标函数和所有的约束函数都为线性函数,则该问题为线性规划问题(Linear Programming,LP)。
- 如果目标函数或任何一个约束函数为非线性函数,则该问题为非线性规划问题(Nonlinear Programming,NLP)。在非线性优化问题中,有一类比较特殊的问题是凸优化问题(Convex Programming)。凸优化问题是一种特殊的约束优化问题,需满足目标函数为凸函数,约束条件为凸集,即对于集合中任意两点,它们的连线全部位于在集合内部。在凸优化中,如果目标函数是关于变量的二次函数,那此类问题称为二次规划问题(Quadratic programming,QP)。
求解
对于最优化问题的求解可谓是一门艺术,无数数学家将实际问题抽象成一个数学问题,并对此提出了各种各样的求解算法,那么最常见、经典的求解方法主要有以下几种:精确算法、近似算法和启发式算法。
- 精确算法是指能够求出问题最优解的算法。当问题的规模较小时,精确算法能够在可接受的时间内得到最优解;当问题的规模较大时,精确算法一方面可以提供问题的可行解,另一方面可以为启发式算法提供初始解,以便搜索到更好的解。精确算法有分支定界法、割平面法、动态规划法等。
- 近似算法是指用近似方法来解决优化问题的算法,通常与 NP-hard 问题相关,由于无法有效地在多项式时间内精确地求得最优解,所以考虑在多项式时间内求得一个有质量保证的近似解。近似算法包括贪婪算法、局部搜索算法、松弛算法等。
- 启发式算法是一种基于直观或经验构造的算法,能在可接受的计算成本内尽可能地逼近最优解,得到一个相对优解,但无法预计所得解与最优解的近似程度。启发式算法可分为传统启发式算法和元启发式算法,传统启发式算法包括构造性方法、局部搜索算法、松弛方法和解空间缩减算法等。元启发式算法包括禁忌搜索算法、模拟退火算法、遗传算法、蚁群算法、粒子群算法和人工神经网络等。
相关最优化问题的求解软件或算法库有:lingo、Matlab、Python(Gurobi、pulp)等等。
相关文章:

数学建模:最优化问题及其求解概述
数学建模:最优化问题及其求解概述 最优化问题定义分类离散优化问题连续优化问题 求解 此博客围绕运筹学以及最优化理论的相关知识,通俗易懂地介绍了最优化问题的定义、分类以及求解算法。 最优化问题 定义 数学优化(Mathematical Optimiza…...

企业办理CS资质,怎么选择办理等级?
信息系统建设和服务能力等级证书(Information system construction and service—Capability assessment system,简称:CS),由中国电子信息行业联合会组织开展的第三方评估活动,是根据《信息系统建设和服务能…...

华为云云耀云服务器L实例评测|Huawei Cloud EulerOS 自动化环境部署
[toc] Huawei Cloud EulerOS 自动化环境部署 云耀云服务器L实例【Huawei Cloud EulerOS 2.0 64bit】 Python Git Google Chrome Chromedriver Selenium More… 1. Python 镜像创建后自带。 2.Git 拉取项目。 sudo yum install git3. Google Chrome 使用root权限或sudo权…...
从一张表格开始做挖机报价系统
一、前言 历时4个月的挖机销售报价系统进入收尾阶段,由我直接负责与业务方对接,这中间各种折腾真是一言难尽,项目开发过程中还要维护POS系统以及牛奶配送系统,本项目我们采用的是迭代开发,今天讲一下具体的开发过程以…...
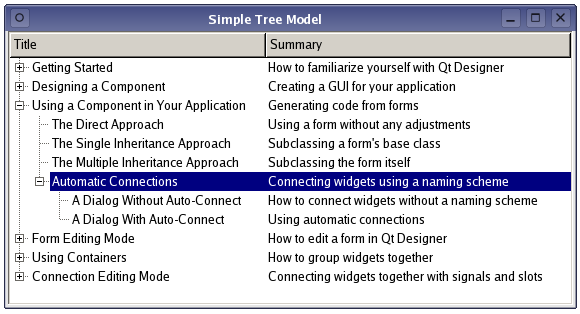
Qt扫盲-QTreeView 理论总结
QTreeView 理论使用总结 一、概述二、快捷键绑定三、提高性能四、简单实例1. 设计与概念2. TreeItem类定义3. TreeItem类的实现4. TreeModel类定义5. TreeModel类实现6. 在模型中设置数据 一、概述 QTreeView实现了 model 中item的树形表示。这个类用于提供标准的层次列表&…...

BF算法详解(JAVA语言实现)
目录 BF算法的介绍 图解 JAVA语言实现 BF算法的时间复杂度 BF算法的介绍 BF算法,即暴力(Brute Force)算法,是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继…...

零基础转行网络工程师,过来人给的一些建议
最近收到好多同学的一些提问,零基础没经验,能不能转行到网络工程师?薪资能有多少?发展前景怎么样? 应该有不少朋友都有这个疑问,那么,今天我尽量给大家做出一个详细的解答,希望能有…...

Vue中如何进行分布式搜索与全文搜索(如Elasticsearch)
在Vue中实现分布式搜索与全文搜索(使用Elasticsearch) 分布式搜索和全文搜索在现代应用程序中变得越来越重要,因为它们可以帮助用户快速查找和检索大量数据。Elasticsearch是一种强大的分布式搜索引擎,它可以用于实现高性能的全文…...
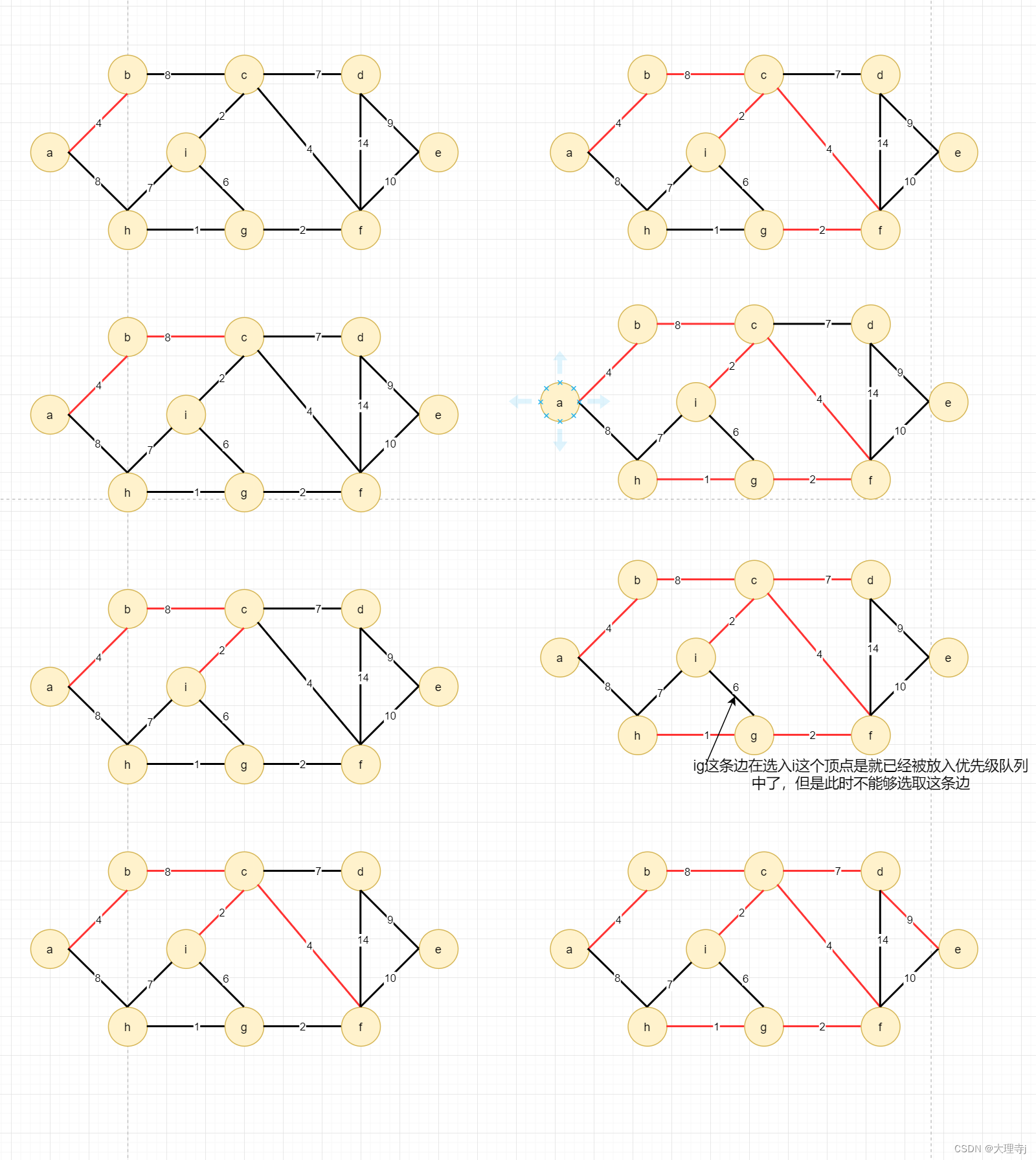
数据结构-图-最小生成树问题
最小生成树 并查集定义举例说明查找某个元素属于哪个集合代码实现路径压缩 Kruskal算法原理代码实现 Prim算法原理代码实现 并查集 定义 🚀在一些应用问题中,需要将n个不同的元素分成一些不相交的集合。开始时,每个元素自成一个单元素集合&…...
使用vite+npm封装组件库并发布到npm仓库
组件库背景:使用elementplusvue封装了一个通过表单组件。通过JSX对el-form下的el-input和el-button等表单进行统一封装,最后达到,通过数据即可一键生成页面表单的功能。 1.使用vite创建vue项目 npm create vitelatest elementplus-auto-form…...

85.最大矩形
单调栈,时间复杂度o(mn),空间复杂度o(mn) class Solution { public:int maximalRectangle(vector<vector<char>>& matrix) {int mmatrix.size();if(m0){return 0;}int nmatrix[0].size();//记录矩阵中每个元素左边连续1的数量vector<…...
Windows服务器 开机自启动服务
1、新建txt,并粘贴下面脚本 start cmd /k "cd /d D:\ahjd&&java -jar clips-admin.jar" start cmd /k "cd /d D:\ahjd\dist&&simple-http-server.exe -i -p 8000"说明,脚本格式为:start cmd /k “cd /d…...

《算法通关之路》chapter17一些通用解题模板
《算法通关之路》学习笔记,记录一下自己的刷题过程,详细的内容请大家购买作者的书籍查阅。 1 二分法 1.1 普通二分法 # 查找nums数组中元素值为target的下标。如果不存在,则返回-1def bs(nums: list[int], target: int) -> int :l, h …...
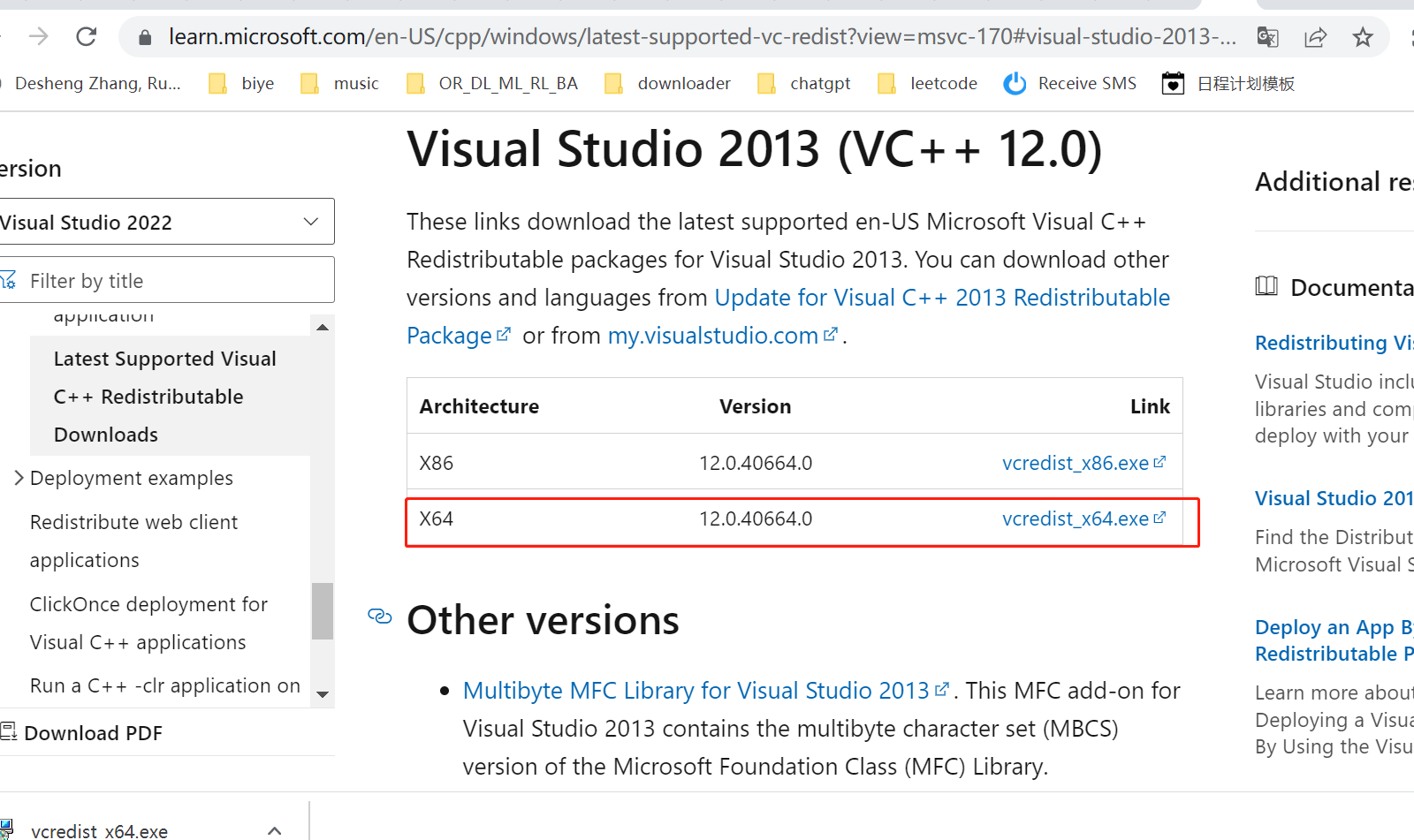
常用求解器安装
1 建模语言pyomo Pyomo是一个Python建模语言,用于数学优化建模。它可以与不同的求解器(如Gurobi,CPLEX,GLPK,SCIP等)集成使用,以求解各种数学优化问题。可以使用Pyomo建立数学优化模型…...
)
第三章:最新版零基础学习 PYTHON 教程(第一节 - Python 运算符)
在Python编程中,运算符一般用于对值和变量进行操作。这些是用于逻辑和算术运算的标准符号。在本文中,我们将研究不同类型的Python 运算符。 运算符:这些是特殊符号。例如- + 、 * 、 / 等。操作数:它是应用运算符的值。目录 Python 中的运算符类型 Python 中的算术运算符…...
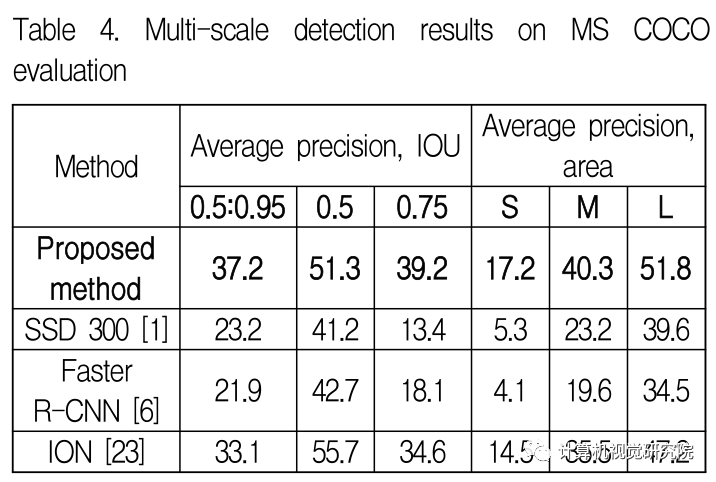
细粒度特征提取和定位用于目标检测:PPCNN
1、简介 近年来,深度卷积神经网络在计算机视觉上取得了优异的性能。深度卷积神经网络以精确地分类目标信息而闻名,并采用了简单的卷积体系结构来降低图层的复杂性。基于深度卷积神经网络概念设计的VGG网络。VGGNet在对大规模图像进行分类方面取得了巨大…...

【STM32单片机】数学自动出题器设计
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用STM32F103C8T6单片机控制器,使用按键、IIC OLED模块等。 主要功能: 系统运行后,OLED液晶显示出题器开机界面,默认结果范围为100,可按…...
C语言之动态内存管理篇(1)
目录 为什么存在动态内存分配 动态内存函数的介绍 malloc free calloc realloc 常见的动态内存错误 今天收假了,抓紧时间写几篇博客。我又来赶进度了。今天我们来讲解动态内存管理。🆗🆗 为什么存在动态内存分配 假设我们去实现一个…...
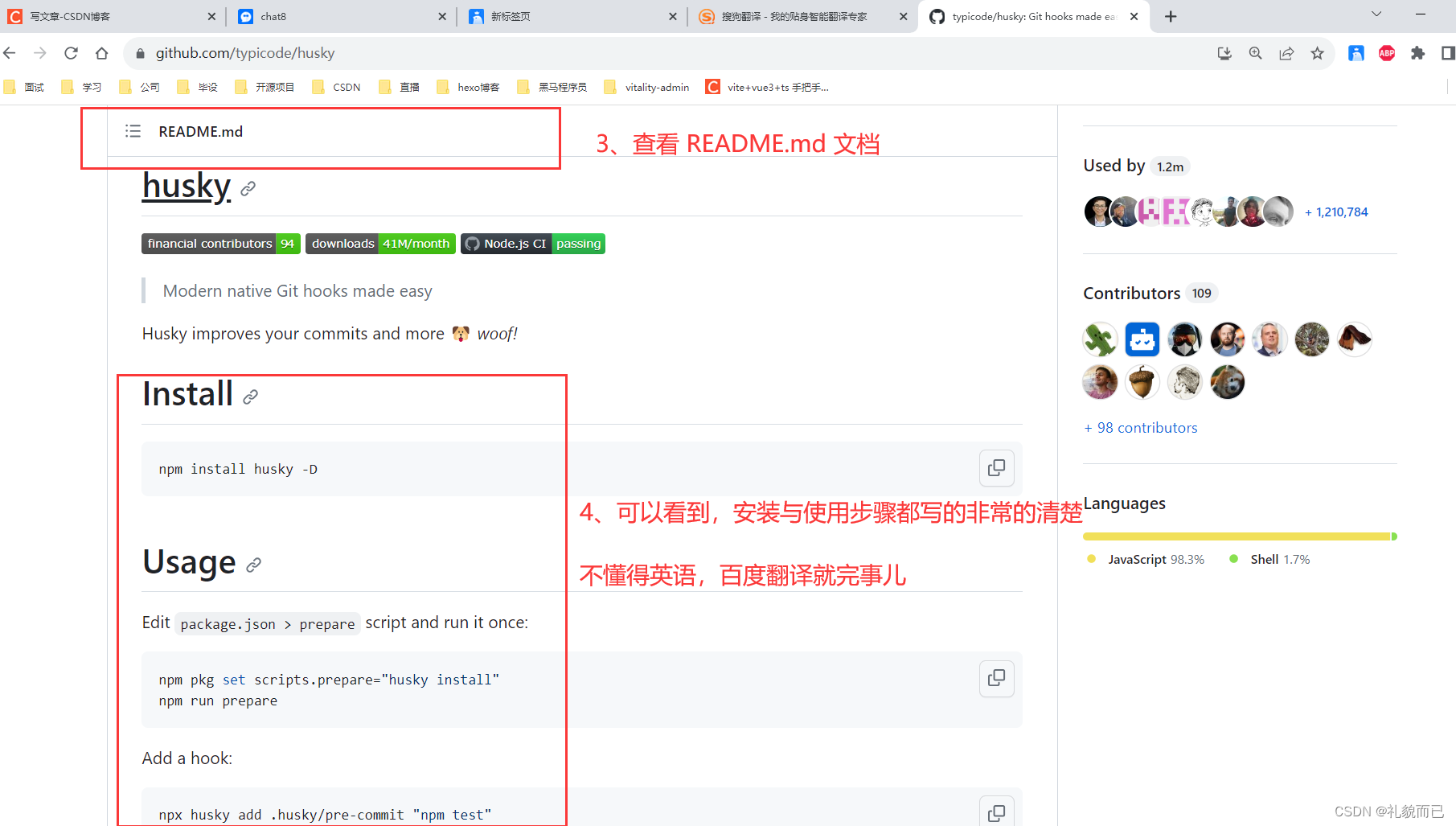
React18入门(第二篇)——React18+Ts项目配置husky、eslint、pretttier、commitLint
前言 我的项目版本如下: React: V18.2.0Node.js: V16.14.0TypeScript:最新版工具: VsCode 本文将采用图文详解的方式,手把手带你快速完成在React项目中配置husky、prettier、commitLint,实现编码规范的统…...
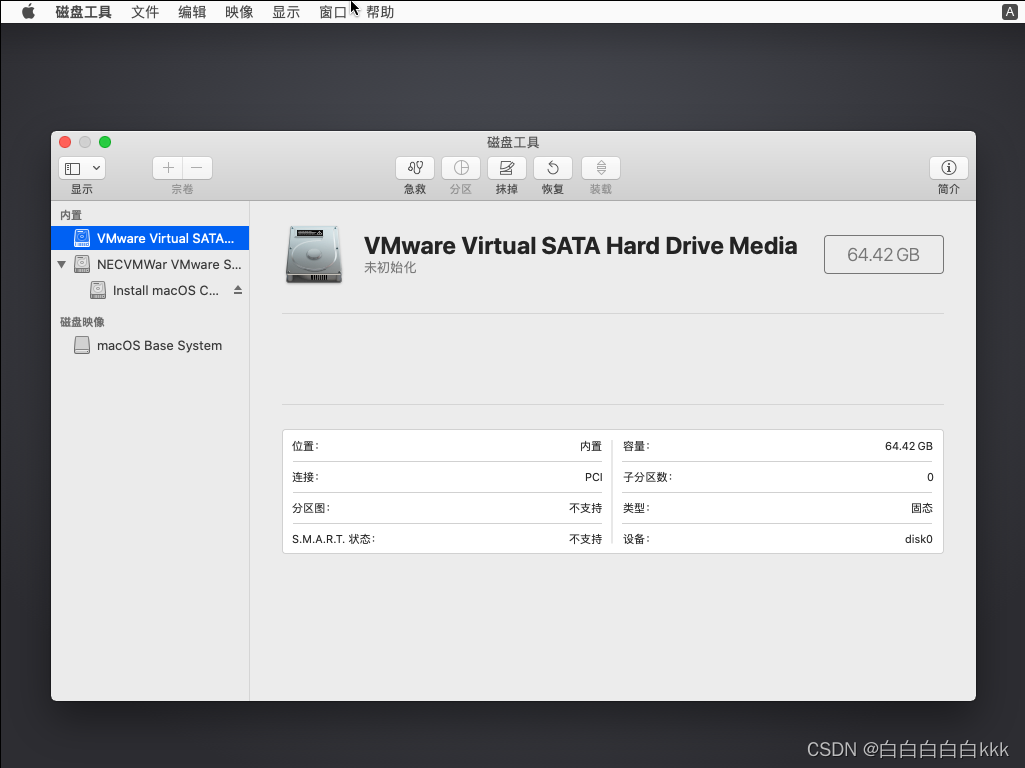
【VINS】苹果手机采集单目相机+IMU数据离线运行VINS-Mono
0.准备工作 开个新坑,之前用Android手机做过离线采集数据的实验,这次用IPhone来测试! 1.虚拟机配置Mac OS 下载一个Mac OS 的ios镜像,打开虚拟机按照跟Ubuntu差不多的方式安装,但是发现没有Mac OS的入口。 因为VMwa…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...
