算法题:买卖股票的最佳时机含手续费(动态规划解法贪心解法-详解)
这道题有两种解法:动态规划 or 贪心算法。
贪心算法的提交结果要比动态规划好一些,总体上动态规划的解法更容易想到。(完整题目附在了最后)
1、动态规划解法
设置两个数,dp[0]表示遍历到股票prices[i]时手里没有股票情况下的纯利润(要么就是无操作,要么就是卖掉手里的股票,卖掉股票是要减去fee,两种操作之间选择利益最大的做法); dp[1]表示遍历到股票prices[i]时手里有股票情况下的纯利润(在“无操作”和“购入当前股票”两种做法之间选择利益最大的做法),那么遍历到股票prices[i+1]时,
dp = [max(dp[0], dp[1] + prices[i] - fee), max(dp[1], dp[0] - prices[i])]。
根据整体意思,dp初始化时为 [0, -prices[0]]。
# 动态规划解法
class Solution(object):def maxProfit(self, prices, fee):n = len(prices)dp = [0, -prices[0]]for i in range(1, n):dp = [max(dp[0], dp[1] + prices[i] - fee), max(dp[1], dp[0] - prices[i])]return max(dp)2、贪心解法
1)在连续递减的情况下买入价格最低时的股票,在不亏本的情况下如果连续递增则在最高点卖掉股票(因为要多考虑一个fee的费用,所以不亏本的前提要加上)。
2)代码有点弯弯绕在里面,就是在还没买入的时候我们把手续费fee加到当前股票价格price上面,遍历prices数组,判断各个相邻price+fee后的大小,在连续递减的情况下选择最低点的买入。
3)买入之后就要寻找最高点卖出,我们继续往后遍历,找到卖出能够有利润的第一支股票,设置一个“虚拟卖出”,由于后面的股票价格可能更高,所以这里不一定是当前这笔交易最后卖出的价格。如果后面的股票价格更高,则把价格差加入到profit里面,直到股票价格开始下降,当前交易才算完成,购入点为最低点,卖出点为有利润的情况下的最高点。
4)重复2)与3)中的买入卖出步骤,直到遍历完prices数组。
# 贪心解法
class Solution:def maxProfit(self, prices, fee):n = len(prices)profit = 0budget = prices[0] + feefor i in range(1, n):if prices[i] + fee < budget:budget = prices[i] + feeelif prices[i] > budget:profit += prices[i] - budgetbudget = prices[i]return profit3、完整题目:
714. 买卖股票的最佳时机含手续费
给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
示例 1:
输入:prices = [1, 3, 2, 8, 4, 9], fee = 2 输出:8 解释:能够达到的最大利润: 在此处买入 prices[0] = 1 在此处卖出 prices[3] = 8 在此处买入 prices[4] = 4 在此处卖出 prices[5] = 9 总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8
示例 2:
输入:prices = [1,3,7,5,10,3], fee = 3 输出:6
提示:
1 <= prices.length <= 5 * 10^41 <= prices[i] < 5 * 10^40 <= fee < 5 * 10^4
相关文章:

算法题:买卖股票的最佳时机含手续费(动态规划解法贪心解法-详解)
这道题有两种解法:动态规划 or 贪心算法。 贪心算法的提交结果要比动态规划好一些,总体上动态规划的解法更容易想到。(完整题目附在了最后) 1、动态规划解法 设置两个数,dp[0]表示遍历到股票prices[i]时手里没有股…...

【gcc】RtpTransportControllerSend学习笔记 4:码率分配
本文是woder大神 的文章的学习笔记。 大神的webrtc源码分析(8)-拥塞控制(上)-码率预估 详尽而具体,堪称神作。 gcc保障带宽公平性,预估码率后要分配码率,实现qos效果: webrtc源码分析(9)-拥塞控制(下)-码率分配 是 woder 大神进一步给出的另一篇神作。 本文是对(https://w…...

「专题速递」AR协作、智能NPC、数字人的应用与未来
元宇宙是一个融合了虚拟现实、增强现实、人工智能和云计算等技术的综合概念。它旨在创造一个高度沉浸式的虚拟环境,允许用户在其中交互、创造和共享内容。在元宇宙中,人们可以建立虚拟身份、参与虚拟社交,并享受无限的虚拟体验。 作为互联网大…...

什么是基于意图的网络(IBN)
基于意图的网络是一种网络技术,它根据业务意图(来自网络管理员的服务请求)配置 IT 基础架构,无需任何人工干预,它不断提供关键的网络见解,并不断调整硬件配置以确保满足意图,它将网络从以设备为…...
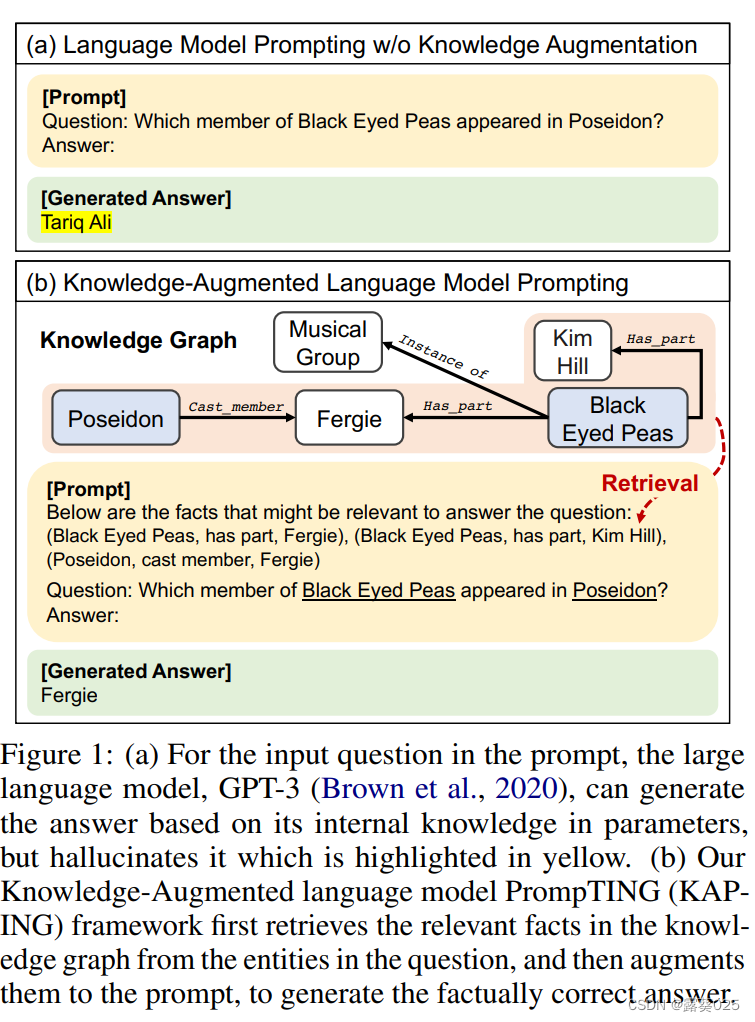
知识增强语言模型提示 零样本知识图谱问答10.8
知识增强语言模型提示 零样本知识图谱问答 摘要介绍相关工作方法零样本QA的LM提示知识增强的LM提示与知识问题相关的知识检索 摘要 大型语言模型(LLM)能够执行 零样本closed-book问答任务 ,依靠其在预训练期间存储在参数中的内部知识。然而&…...

虚拟现实项目笔记:SDK、Assimp、DirectX Sample Browser、X86和X64
文章目录 SDK是什么Assimp是什么DirectX Sample Browser是什么X86和X64生成解决方案和重新生成解决方案 SDK是什么 SDK是Software Development Kit的英文缩写,意思是软件开发包。 软件开发包中往往包含有多种辅助进行软件开发的内容,包括一些软件开发工…...
openwrt rm500u ncm方式拨号步骤记录
1.进入设备页面 用户名:root 2.创建接口 3.配置接口 国内APN 信息 中国移动APN:CMNET 中国联通APN:3GNET 中国电信APN:CTNET 4.防火墙配置 5.点击Save&Apply 6.配置完成后重启设备。重新进入设备页面,可以看…...

使用js代码将一个值为“1=增量,2=全量“的字符串转化为一个数组,数据格式为[{value:““,label:“‘‘}]
const str "1增量,2全量"; const arr str.split(",").map(item > {const [value, label] item.split("");return { value, label}; });...

图片调色盘
图片预览 配置安装 Color-Thief 安装包使用文档 yarn add colorthief -S // npm install colorthief --save代码 <template><div class"img-thief"><div class"container"><div class"thief-item" v-for"(item, in…...
一文读懂Base64
这几天在和第三方交互的时候,对方返回的数据是base64格式的数据,所以这两天又彻底捋了下Base64的来龙去脉。之前看过一篇文章说的非常好(再找到给加上链接),我在这不详细说明了,只说转换过程。 还是使用中…...

CCF CSP认证 历年题目自练 Day20
题目一 试题编号: 201903-1 试题名称: 小中大 时间限制: 1.0s 内存限制: 512.0MB 问题描述: 题目分析(个人理解) 常规题目,先看输入,第一行输入n表示有多少数字&am…...

【Overload游戏引擎分析】从视图投影矩阵提取视锥体及overload对视锥体的封装
overoad代码中包含一段有意思的代码,可以从视图投影矩阵逆推出摄像机的视锥体,本文来分析一下原理 一、平面的方程 视锥体是用平面来表示的,所以先看看平面的数学表达。 平面方程可以由其法线N(A, B, C)和一个点Q(x0,…...

vue全局事件总线是什么?有什么用?解决了什么问题,与pinia有什么区别?
全局事件总线快速入门 概念基本概念(是什么?)核心概念 核心特性和优势(有什么用?)解决了什么问题?主要优势是什么? 案例演示?传递数据-案例演示传递事件-案例演示 与pinia有什么区别?…...
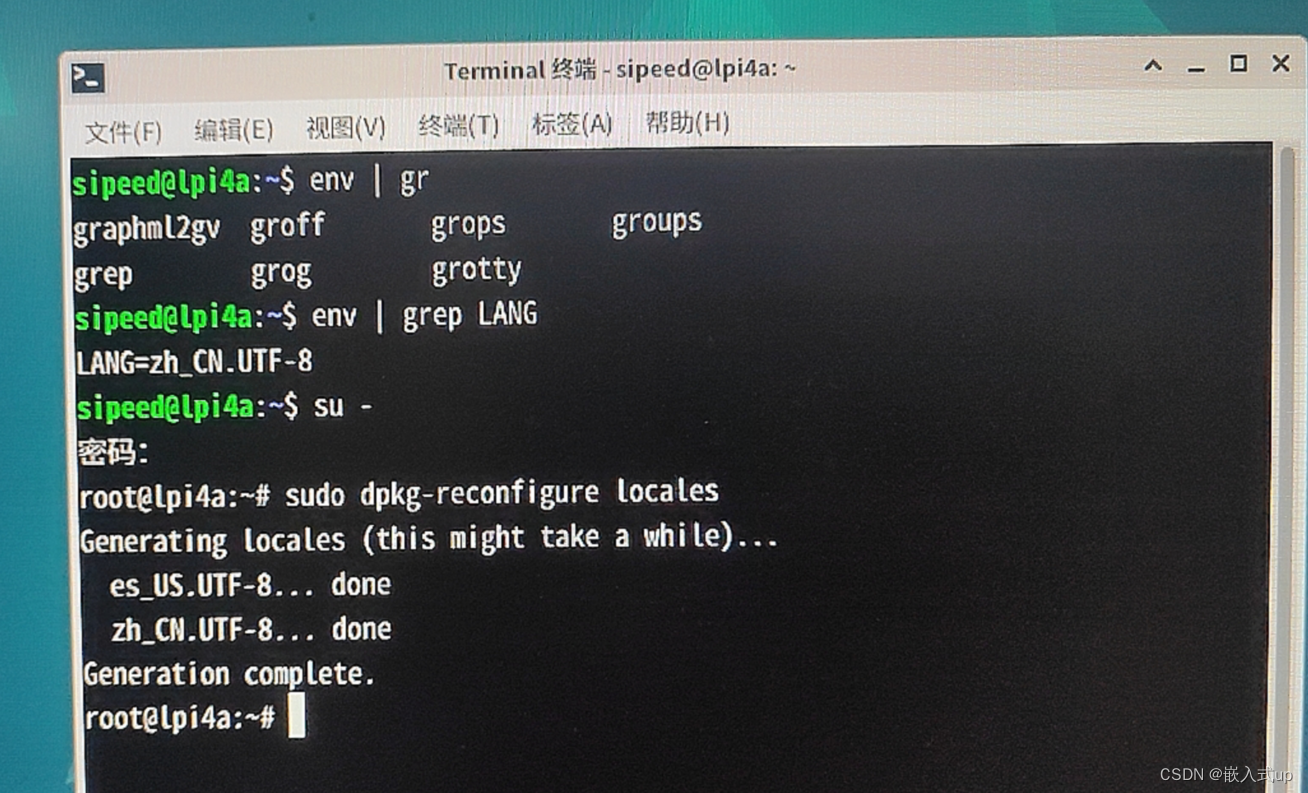
【debian 12】:debian系统切换中文界面
目录 目录 项目场景 基础参数 原因分析 解决方案 1.ctrlaltT 打开终端 2.查询当前语言环境(我的已经设置成了中文 zh_CN.UTF-8) 3.打开语言配置界面 4.最后一步:重启 不要放弃任何一个机会! 项目场景: 这两…...
)
es官方为我们提供的堆内存保护机制-熔断器( breaker )
总熔断器(相当于似乎总闸) 参数: indices.breaker.total.use_real_memory 默认值:true 在 elasticsearch.yml中配置。 参数: indices.breaker.total.limit 如果 indices.breaker.total.use_real_memory : true, in…...

靶场通关记录
OSCP系列靶场-Esay-CyberSploit1 总结 getwebshell → 源码注释发现用户名 → robots.txt发现base64密码 → SSH登录 提 权 思 路 → 内网信息收集 → 发现发行版本有点老 → 内核overlayfs提权 准备工作 启动VPN 获取攻击机IP > 192.168.45.220 启动靶机 获取目标机器I…...
全网最新最全的软件测试面试题
一、前言 与开发工程师相比,软件测试工程师前期可能不会太深,但涉及面还是很广的。 在一年左右的实习生或岗位的早期面试中,主要是问一些基本的问题。 涉及到的知识主要包括MySQL数据库的使用、Linux操作系统的使用、软件测试框架问题、测试…...
如何列出 Ubuntu 和 Debian 上已安装的软件包
当你安装了 Ubuntu 并想好好用一用。但在将来某个时候,你肯定会遇到忘记曾经安装了那些软件包。 这个是完全正常。没有人要求你把系统里所有已安装的软件包都记住。但是问题是,如何才能知道已经安装了哪些软件包?如何查看安装过的软件包呢&a…...

图论---最小生成树问题
在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。解决最小生成树问题一般有两种算法:Kruskal算法和Prim算法。 Kruskal算法 原理:基本思想是从小到大加入边,是个贪心算法。我们将图中的每个边按…...

elementplus 时间范围选择器限制选择时间范围
<el-date-pickerv-model"form.time" type"daterange"range-separator"-"start-placeholder"开始时间"end-placeholder"结束":disabled-date"disabledDate"calendar-Change"calendarChange" />co…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
