OBS 进阶 之 摄像头操作
目录
一、摄像头
1、win-dshow插件中,摄像头枚举操作
1)、视频源ID
2)、注册视频源信息
相关文章:

OBS 进阶 之 摄像头操作
目录 一、摄像头 1、win-dshow插件中,摄像头枚举操作 1)、视频源ID 2)、注册视频源信息...
Linux操作系统基础知识命令参数详解
Linux操作系统 RAID分组 RAID JBOD RAID JBOD的意思是Just a Bunch Of Disks,是将多块硬盘串联起来组成一个大的存储设备,从某种意义上说这种类型不被算作RAID,在维基百科里JBOD同时也被归入非RAID架构。RAID JBOD将所有的磁盘串联成一个单…...

Rust中一些K/V存储引擎
K/V存储引擎的由来可以追溯到20世纪70年代的Berkley DB,而近年来,随着互联网应用的发展,KV存储引擎因其简单高效、可扩展性和适合缓存应用等特点,在分布式存储领域得到了广泛应用。而使用Rust编写KV存储具有内存安全、高性能、并发…...
202302-第四周资讯
山川软件愿为您提供最优质的服务。 您的每一个疑问都会被认真对待,您的每一个建议都将都会仔细思考。 我们希望人人都能分析大数据,人人都能搭建应用。 因此我们将不断完善我们的DEMO、文档、以及视频,期望能在最大程度上快速帮助用户快速…...

九方财富冲刺上市:付费用户开始减少,退款金额飙升至4.9亿元
日前,九方财富控股有限公司(下称“九方财富”)通过港交所上市聆讯,并披露了聆讯后招股书。据贝多财经了解,九方财富最早于2021年8月31日在港交所递表,后在2022年3月、9月分别进行了更新。 据每日经济新闻报…...
SSM+HTML搭建(小白教学)
最近做项目,觉得还是有意义记录以下前后端框架是怎么搭建的,今天给大家介绍介绍SSM:SpringBootSpringMVCMyBatis后端搭建:SpringBoot快速搭建的网站(Spring Initializr)选择创建之后,会下载到一个zip压缩包,对压缩包进行解压(包地址一般选择后端项目的放的文件夹中)用idea打开项…...
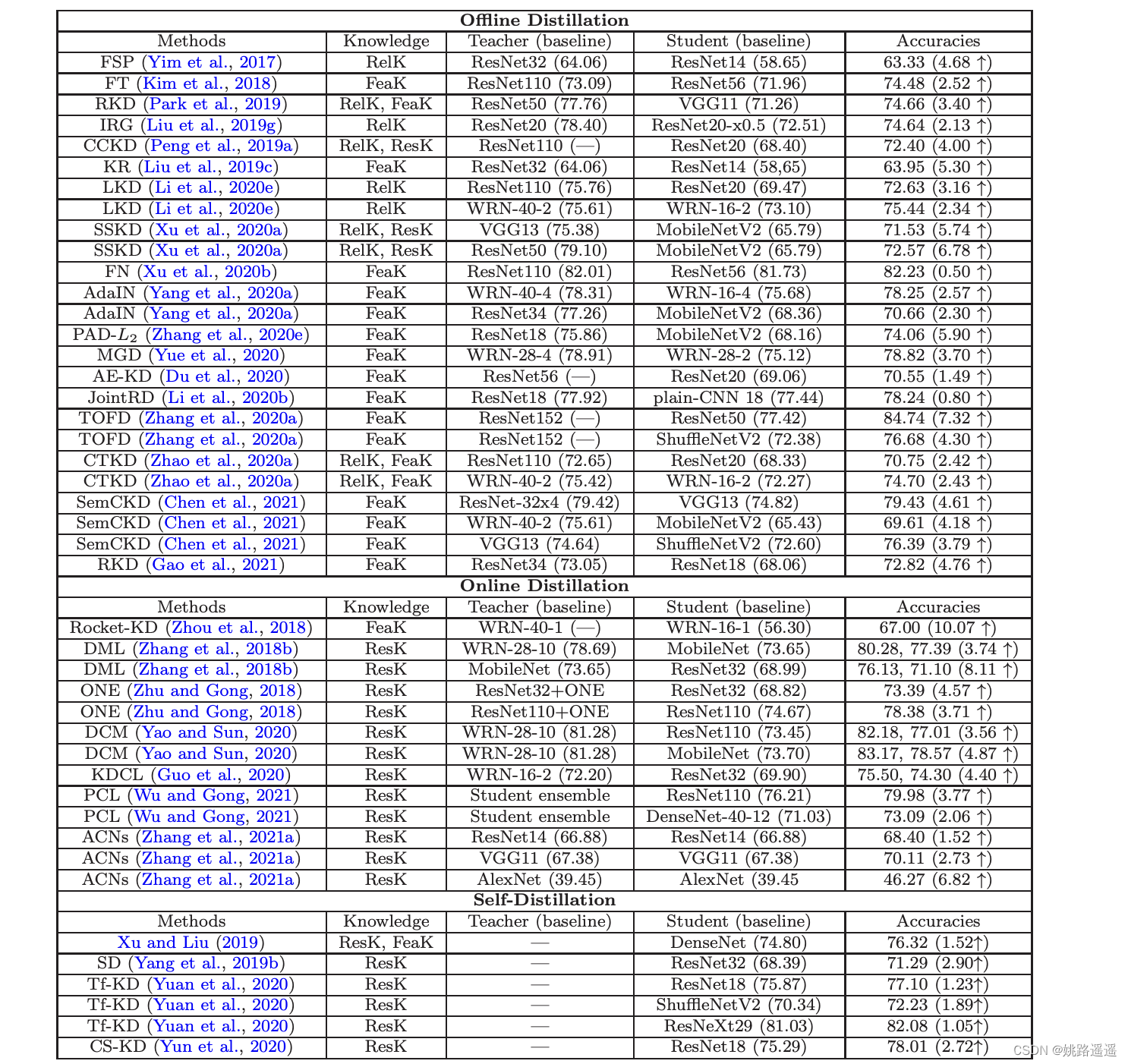
【知识蒸馏】知识蒸馏(Knowledge Distillation)技术详解
参考论文:Knowledge Distillation: A Survey 1.前言 近年来,深度学习在学术界和工业界取得了巨大的成功,根本原因在于其可拓展性和编码大规模数据的能力。但是,深度学习的主要挑战在于,受限制于资源容量࿰…...

公司新招了个腾讯5年经验的测试员,让我见识到什么才是真正的测试天花板····
5年测试,应该是能达到资深测试的水准,即不仅能熟练地开发业务,而且还能熟悉项目开发,测试,调试和发布的流程,而且还应该能全面掌握数据库等方面的技能,如果技能再高些的话,甚至熟悉分…...

(一维、二维)数组传参,(一级、二级)指针传参【含样例分析,新手易懂】
目录数组传参一维数组传参二维数组传参指针传参一级指针传参二级指针传参我们在写代码的时候难免要把数组或者指针传给函数,那函数的参数该如何设计呢? 数组传参 一维数组传参 我们首先来看下面代码的几个例子: #include <stdio.h>…...

for循环中的setTimeout以及var let作用域
看了很多解释,感觉都不好理解。这个文章是我自己的理解,可以做个参考,如果我理解的不对,欢迎在评论区指正: var:使用var声明的变量具有全局作用域 (循环中每次声明的是同一个变量) l…...
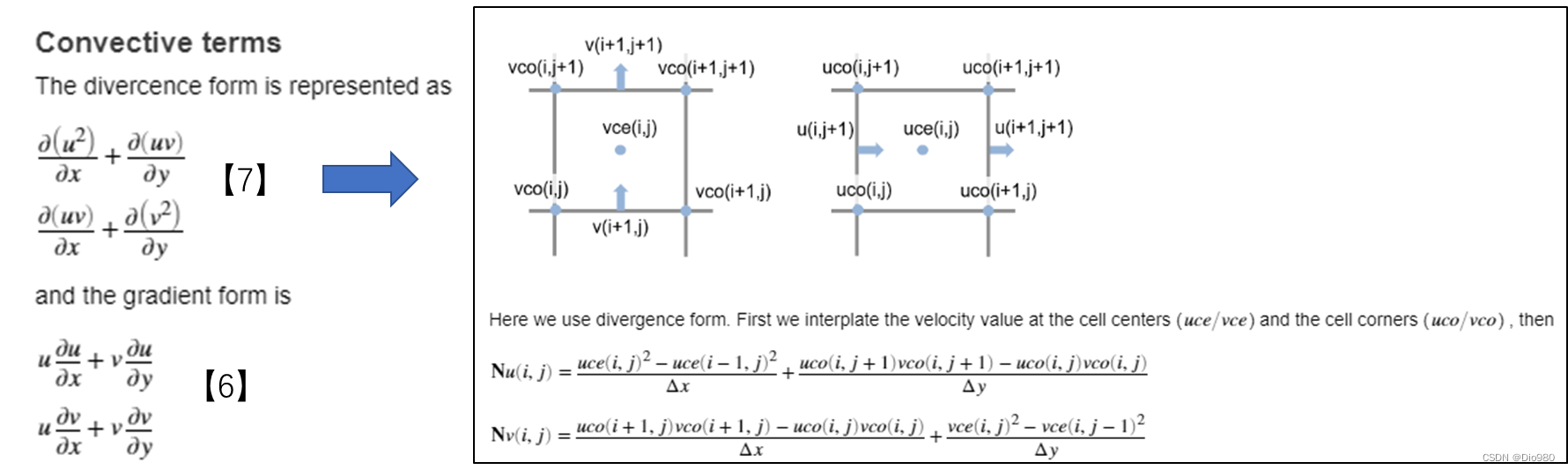
有限差分法求解不可压NS方程
网上关于有限差分法解NS方程的程序实现不尽完备,这里是一些补充注解 现有的优秀资料 理论向 【1】如何从物理意义上理解NS方程? - 知乎 【2】NS方程数值解法:投影法的简单应用 - 知乎 【3】[计算流体力学] NS 方程的速度压力法差分格式_…...
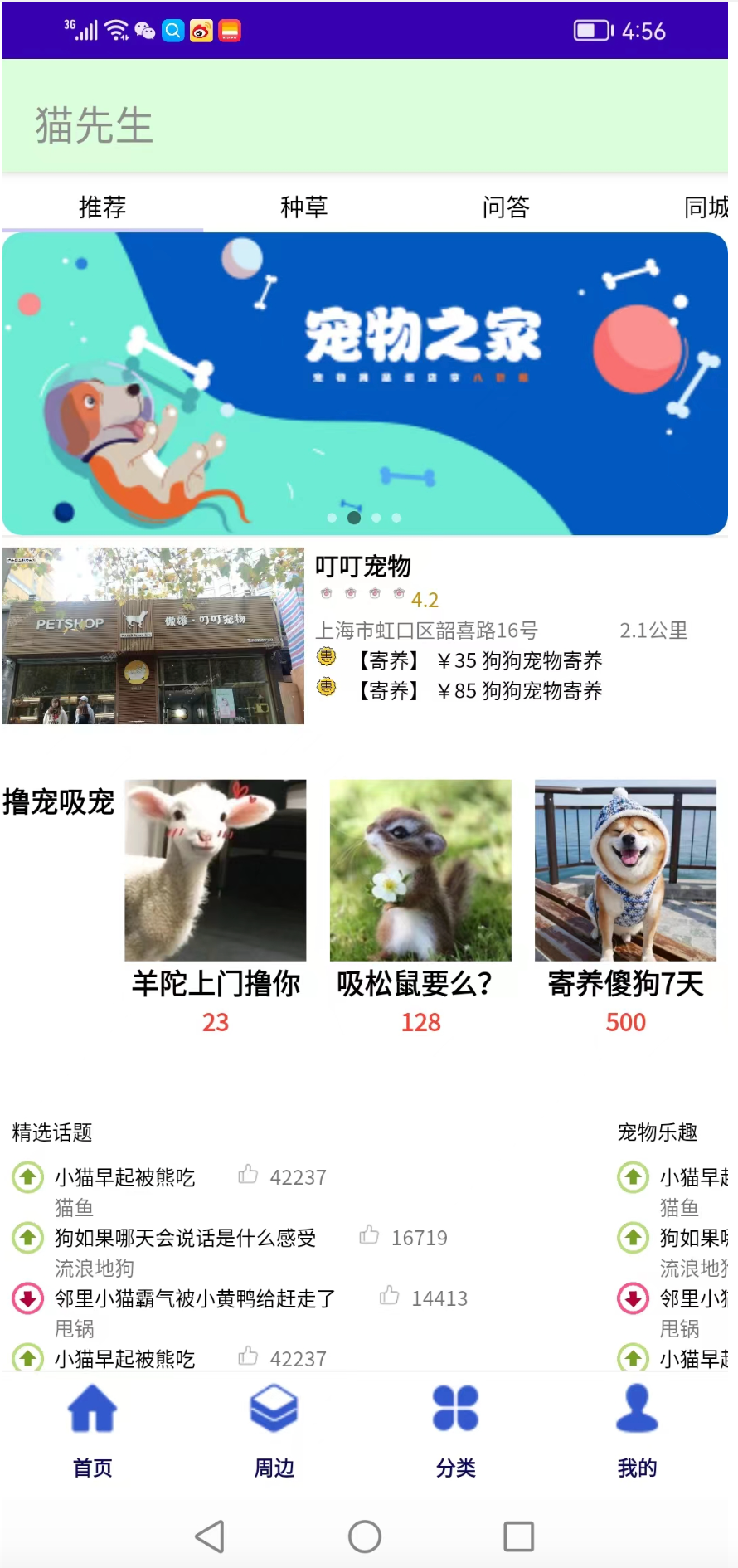
Android入门第66天-使用AOP
开篇这篇恐怕又是一篇补足网上超9成关于这个领域实际都是错的、用不起来的一个知识点了。网上太多太多教程和案例用的是一个叫hujiang的AOP组件-com.hujiang.aspectjx:gradle-android-plugin-aspectjx。首先这些错的文章我不知道是怎么来的,其次那些案例真的运行成功…...

pl/sql篇之触发器
简述本文將具体简述触发器的语法,触发条件及其适用场景,希望对读者理解,使用触发器能起到作用。触发器的定位触发器是数据库独立编译,存储的对象,是数据库重要的技术。和函数不同,触发器的执行是主动的&…...

黑马《数据结构与算法2023版》正式发布
有人的地方就有江湖。 在“程序开发”的江湖之中,各种技术流派风起云涌,变幻莫测,每一位IT侠客,对“技术秘籍”的追求和探索也从未停止过。 要论开发技术哪家强,可谓众说纷纭。但长久以来,确有一技&#…...
Spring的创建和使用
目录 创建Spring项目 步骤 1)使用Maven的方式创建Spring项目 2)添加Spring依赖 3)创建启动类 存Bean对象 1.创建Bean对象 2.将Bean注册到Spring中 取Bean对象并使用 步骤 1.先得到Spring上下文对象 2.从Spring中获取Bean对象 3.使用Bean ApplicationContext VS Bea…...
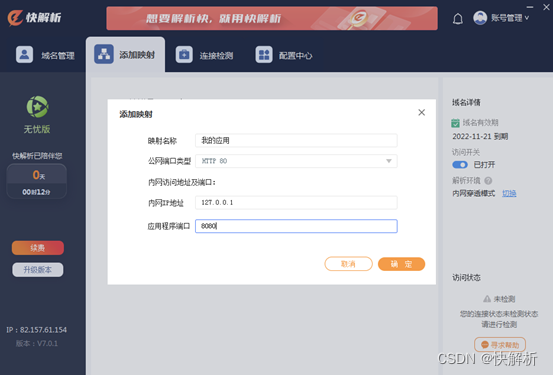
如何实现外网跨网远程控制内网计算机?快解析来解决
远程控制,是指管理人员在异地通过计算机网络异地拨号或双方都接入Internet等手段,连通需被控制的计算机,将被控计算机的桌面环境显示到自己的计算机上,通过本地计算机对远方计算机进行配置、软件安装程序、修改等工作。通俗来讲&a…...

【跟着ChatGPT学深度学习】ChatGPT教我文本分类
【跟着ChatGPT学深度学习】ChatGPT教我文本分类 ChatGPT既然无所不能,我为啥不干脆拜他为师,直接向他学习,岂不是妙哉。说干就干,我马上就让ChatGPT给我生成了一段文本分类的代码,不看不知道,一看吓一跳&am…...

IM即时通讯架构技术:可靠性、有序性、弱网优化等
消息的可靠性是IM系统的典型技术指标,对于用户来说,消息能不能被可靠送达(不丢消息),是使用这套IM的信任前提。 换句话说,如果这套IM系统不能保证不丢消息,那相当于发送的每一条消息都有被丢失的…...

【算法】三道算法题两道难度中等一道困难
算法目录只出现一次的数字(中等难度)java解答参考二叉树的层序遍历(难度中等)java 解答参考给表达式添加运算符(比较困难)java解答参考大家好,我是小冷。 上一篇是算法题目 接下来继续看下算法题…...
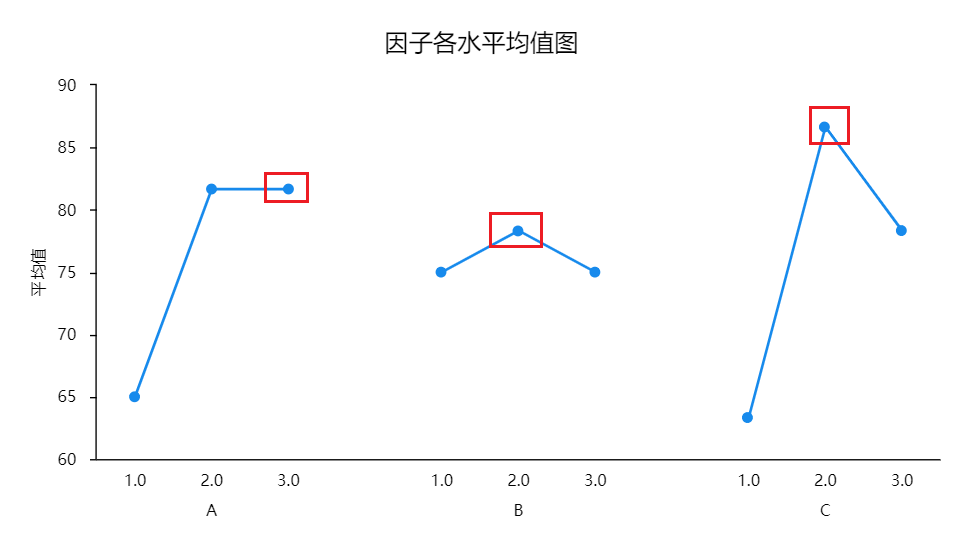
正交实验与极差分析
正交试验极差分析流程如下图: 正交试验说明 正交试验是研究多因素试验的设计方法。对于多因素、多水平的实验要求,如果每个因素的每个水平都要进行试验,这样就会耗费大量的人力和时间,正交试验可以选择出具有代表性的少数试验进行…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
