八大排序算法(含时间复杂度、空间复杂度、算法稳定性)
文章目录
- 八大排序算法(含时间复杂度、空间复杂度、算法稳定性)
- 1、(直接)插入排序
- 1.1、算法思想
- 1.2、排序过程图解
- 1.3、排序代码
- 2、希尔排序
- 3、冒泡排序
- 3.1、算法思想
- 3.2、排序过程图解
- 3.3、排序代码
- 4、(简单)选择排序
- 4.1、算法思想
- 4.2、排序过程图解
- 4.3、排序代码
- 5、堆排序
- 6、快速排序
- 7、归并排序
- 8、计数排序
- 8.1、算法思想
- 8.2、排序过程图解
- 8.3、排序代码

八大排序算法(含时间复杂度、空间复杂度、算法稳定性)
下列算法默认都是对数组进行升序
1、(直接)插入排序
1.1、算法思想
-
插入排序是一种简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序的具体步骤如下:
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。


1.2、排序过程图解
-
从第一个元素开始,该元素可以认为已经被排序,取出下一个元素并记录到临时变量
tmp中,在已经排序的元素序列中从后向前扫描(end--),如果该元素(已排序)大于新元素,将该元素移到下一位置,如果该元素小于等于新元素,则直接在这个元素的后面把新元素放进来。

- 这里仅演示部分过程,其他过程自行考虑(和上述过程类似)。
1.3、排序代码
-
end指向当前要插入元素的前一个位置(end+1指向当前要插入元素的位置),tmp保存当前要插入的元素,在已经排序的元素序列中从后向前扫描,找到比新元素小的元素的时候(因为有序,这个位置前面的元素比这个元素更小),直接把新元素插入到这个位置的后面。//插入排序 void InsertSort(int *arr, int n) {for (int i = 0; i < n - 1; ++i) {//一趟int end = i;int tmp = arr[end + 1];while (end >= 0) {if (tmp < arr[end]) {arr[end + 1] = arr[end];} else {break;}--end;}arr[end + 1] = tmp;} } -
时间复杂度计算:
-
最坏时间复杂度:数组元素原本是降序,现要求使其升序。那么每个元素需要移动或者比较的次数为:
- 第一个元素:
0次 - 第二个元素:
1次 - 第三个元素:
2次 - …
- 第n个元素:
n-1次
总次数:
0+1+2+3+...+n-1 = n*(n-1)/2次所以最坏时间复杂度为:O(n^2)。
- 第一个元素:
-
最好时间复杂度:考虑数组原本是升序,那么所有元素需要移动或者比较的总次数为:
0+1+1+...+1 = n-1。所以最好时间复杂度为O(n)。 -
平均时间复杂度:O(n^2) ----> 算法不太行。
-
-
空间复杂度计算:由于没有开辟额外空间来辅助数组排序,故空间复杂度为O(1)。
-
算法稳定性:稳定,因为对于值相同的元素,后插入的时候不会插到相同元素的前面(
tmp >= arr[end]会break,即不插入)。
2、希尔排序
希尔排序详解
3、冒泡排序
3.1、算法思想
- 冒泡排序是通过对相邻元素的比较和位置交换,使得每次遍历都可以得到剩余元素中的最大值,将其放入有序序列中最终的位置,然后下一趟排序的时候就不用去比较这个已经确定了的元素。在冒泡排序中,会依次比较相邻元素的值,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就如同水底下的气泡一样逐渐向上冒。
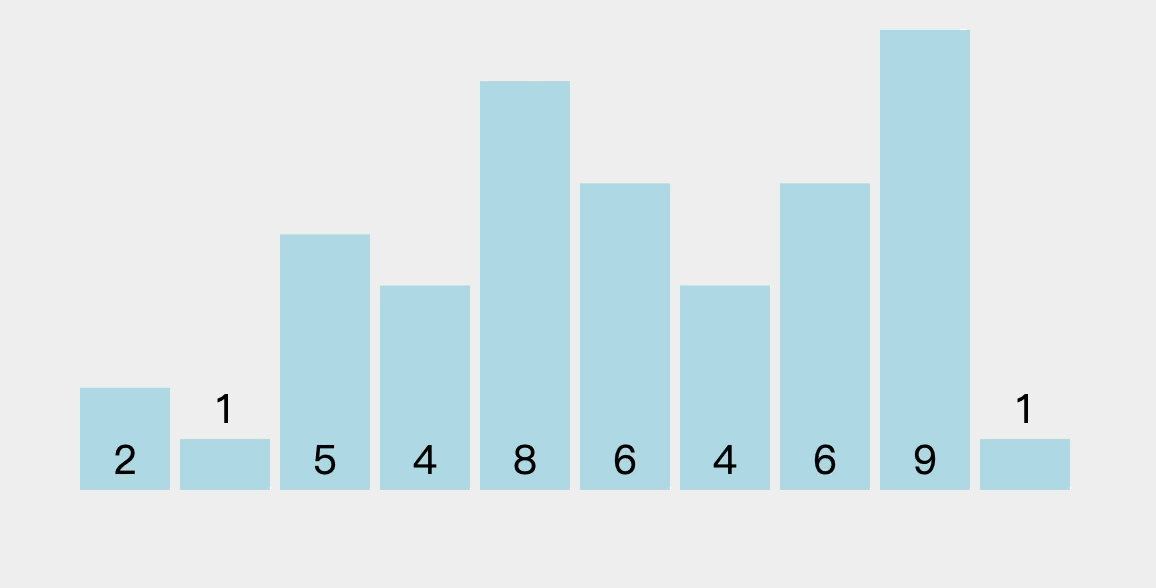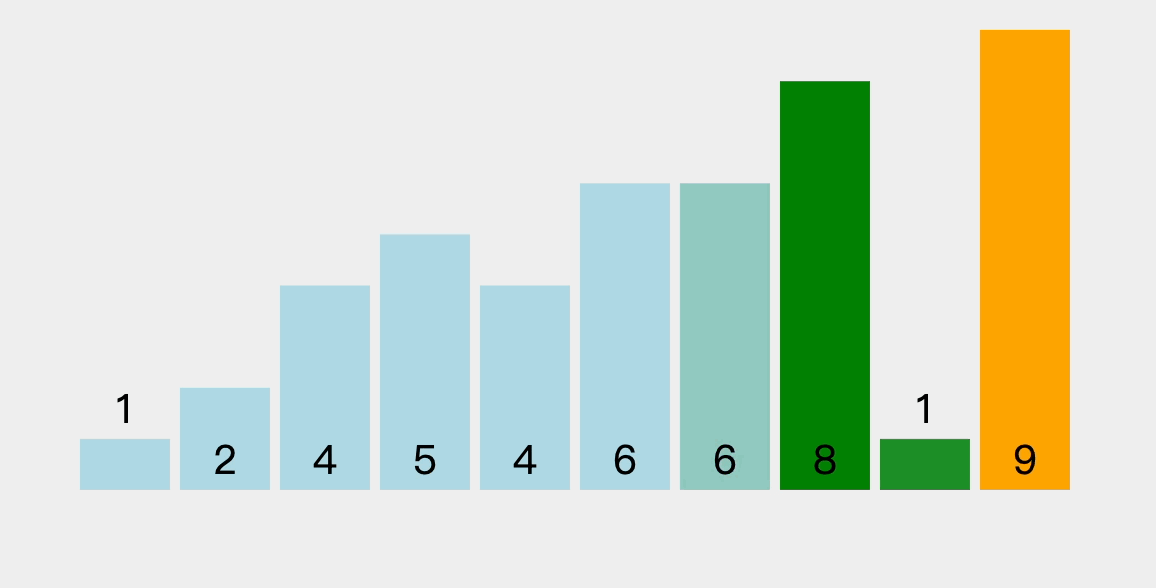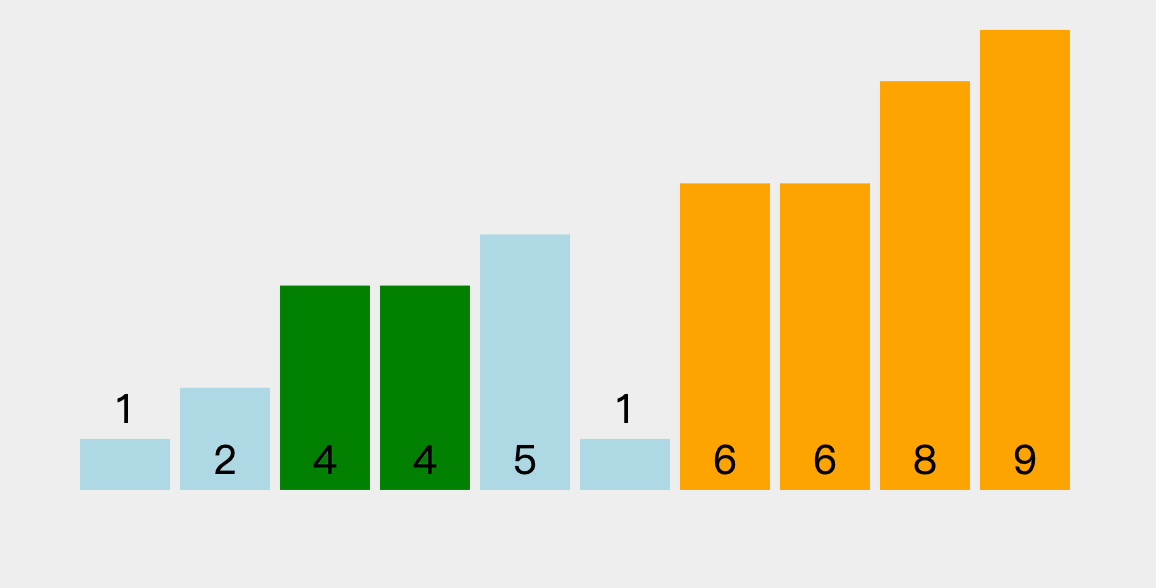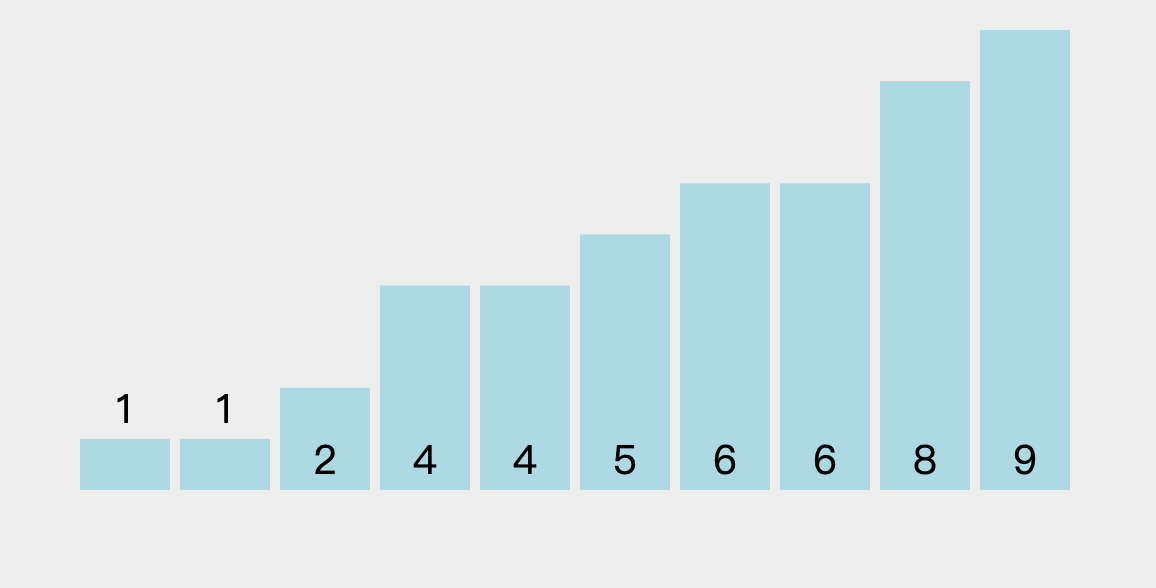
3.2、排序过程图解
-
每趟排序可以把一个元素”冒“到最终位置上,下一趟排序就可以少排序一个元素。


- 这里仅演示部分过程,其他过程自行考虑(和上述过程类似)。
3.3、排序代码
-
指针
i控制每趟需要少排序的元素个数(即已经有i个元素已经在最终位置上),指针j用来比较相邻元素的大小,若相邻元素是降序,则交换这两个元素。 -
这里定义了一个
flag,用来标记每趟排序是否有交换,如果有交换,就需要继续下一趟排序,没有交换则说明数组已经有序,那么就不用继续下一趟排序!void Swap(int *a, int *b) {int tmp = *a;*a = *b;*b = tmp; }//冒泡排序 void BubbleSort(int *arr, int n) {for (int i = 0; i < n; ++i) {int flag = 0;for (int j = 0; j < n - 1 - i; ++j) {if (arr[j + 1] < arr[j]) {flag = 1;Swap(&arr[j], &arr[j + 1]);}}if (flag == 0) {break;}} } -
时间复杂度计算:
-
最坏时间复杂度:考虑数组原本是降序,现在要求其升序。那么每个元素需要移动或者比较的次数为:
- 第一趟排序:
n-1次 - 第二趟排序:
n-2次 - 第三趟排序:
n-3次 - …
- 第n趟排序:
1次
总次数:
n-1+n-2+n-3+...+1 = n*(n-1)/2次所以最坏时间复杂度为:O(n^2)。
- 第一趟排序:
-
最好时间复杂度:考虑数组原本是升序。那么所有元素需要移动或者比较的次数为:
若不使用
flag:比较次数为n-1+n-2+n-3+...+1 = n*(n-1)/2次。使用
flag:比较次数为n-1次。 -
平均时间复杂度:O(n^2) —> 算法不太行。
-
-
空间复杂度计算:由于没有开辟额外空间来辅助数组排序,故空间复杂度为O(1)。
-
算法稳定性:稳定,因为对于值相同的元素,每一趟排序的时候不会交换(
arr[j + 1] < arr[j]才交换)。
4、(简单)选择排序
4.1、算法思想
- 选择排序是一种简单直观的排序算法。它的工作原理如下:(优化后的选择排序–>每次都能确定当前未排序序列的最小元素和最大元素的最终位置)
- 在未排序序列中找到最小元素和最大元素,最小元素存放到排序序列的起始位置,最大元素存放到排序序列的末尾位置。
- 再从剩余未排序元素中继续寻找最小元素和最大元素,然后最小元素放到前面已排序序列的末尾,最大元素放到后面已排序序列的前面。
- 以此类推,直到所有元素均排序完毕。
- 这里动画排序是每次选出一个最小值。(我们讲的算法更优哈哈)
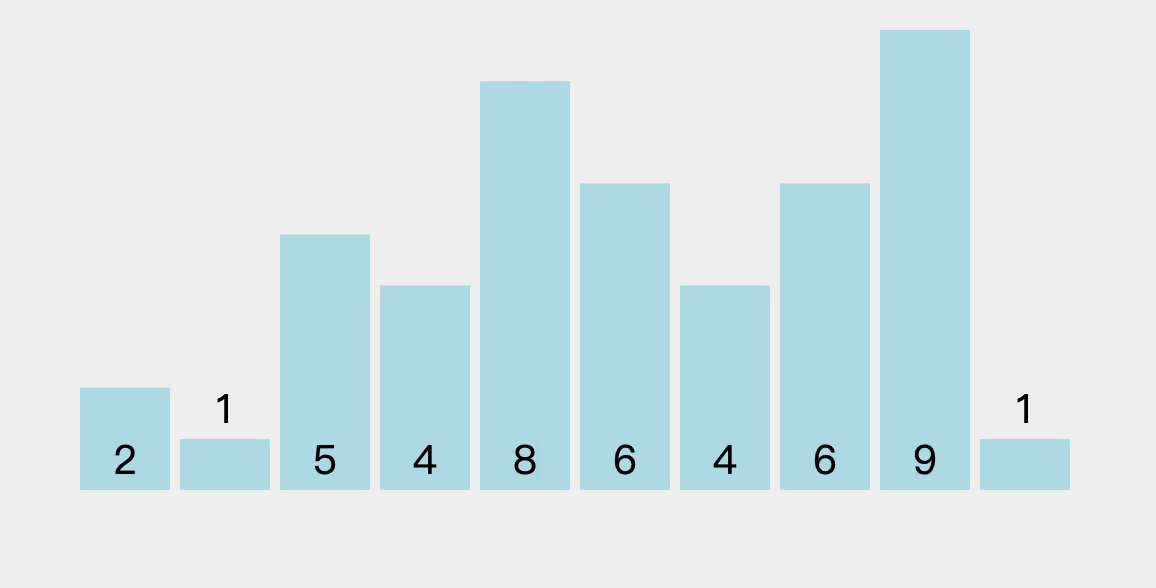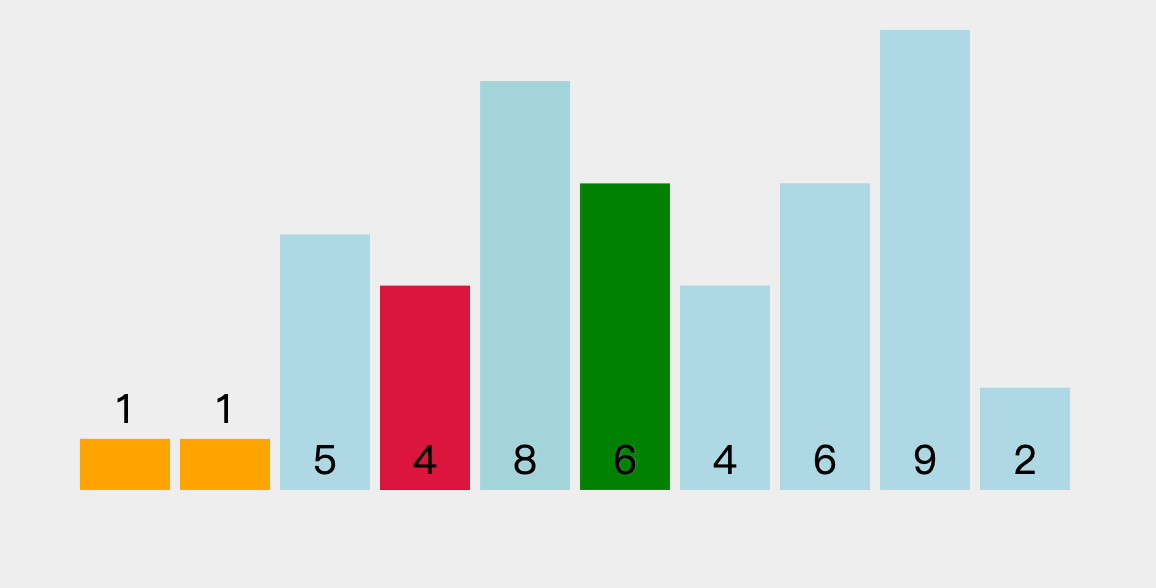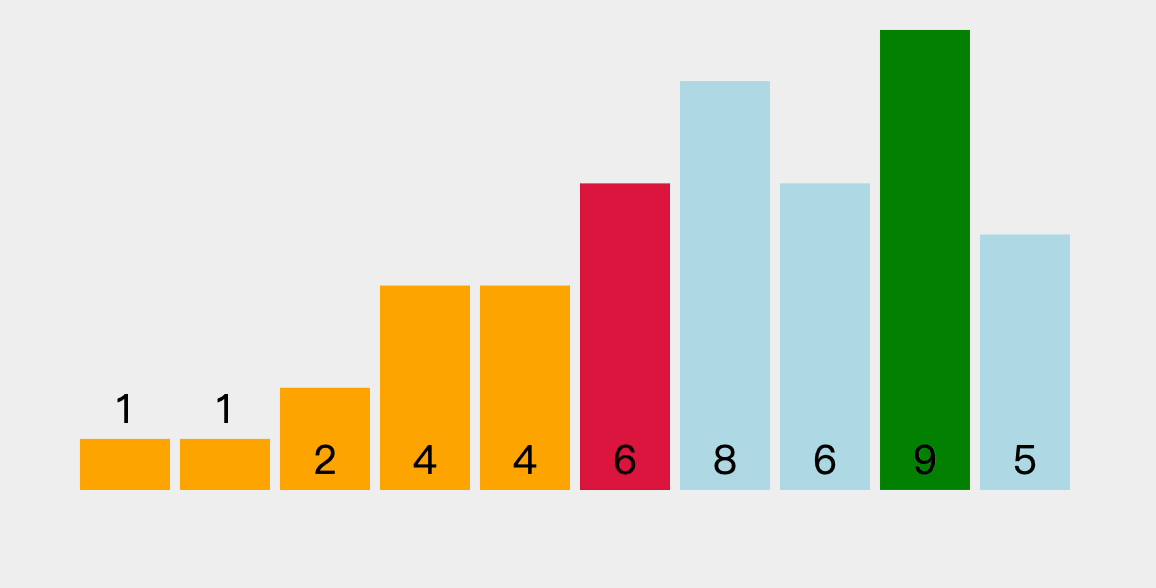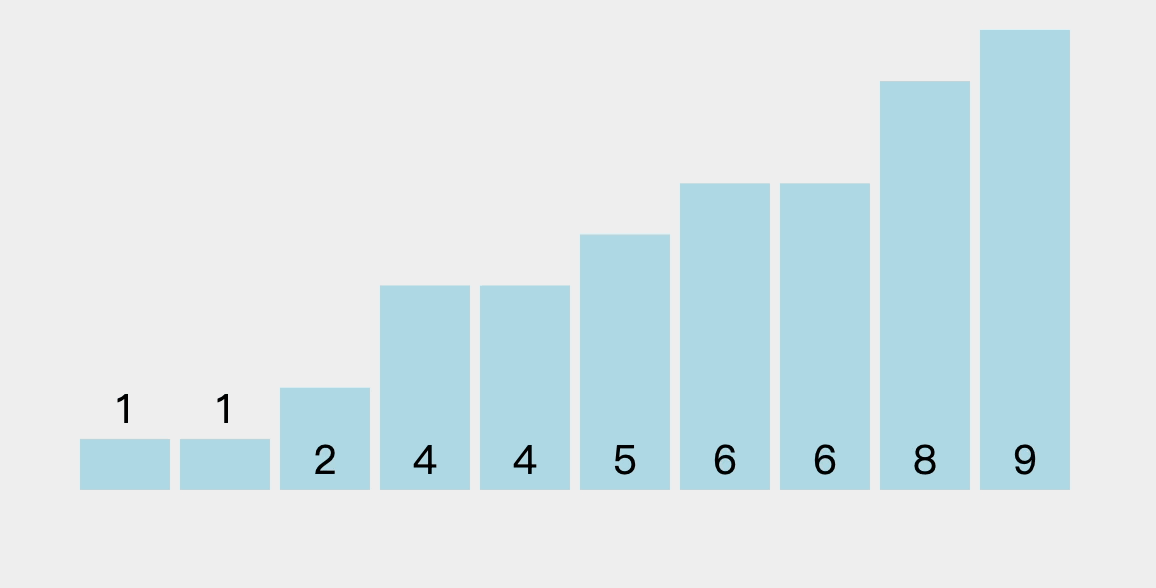
4.2、排序过程图解
-
在未排序序列中找到最小元素和最大元素,最小元素存放到排序序列的起始位置,最大元素存放到排序序列的末尾位置。

-
再从剩余未排序元素中继续寻找最小元素和最大元素,然后最小元素放到前面已排序序列的末尾,最大元素放到后面已排序序列的前面。
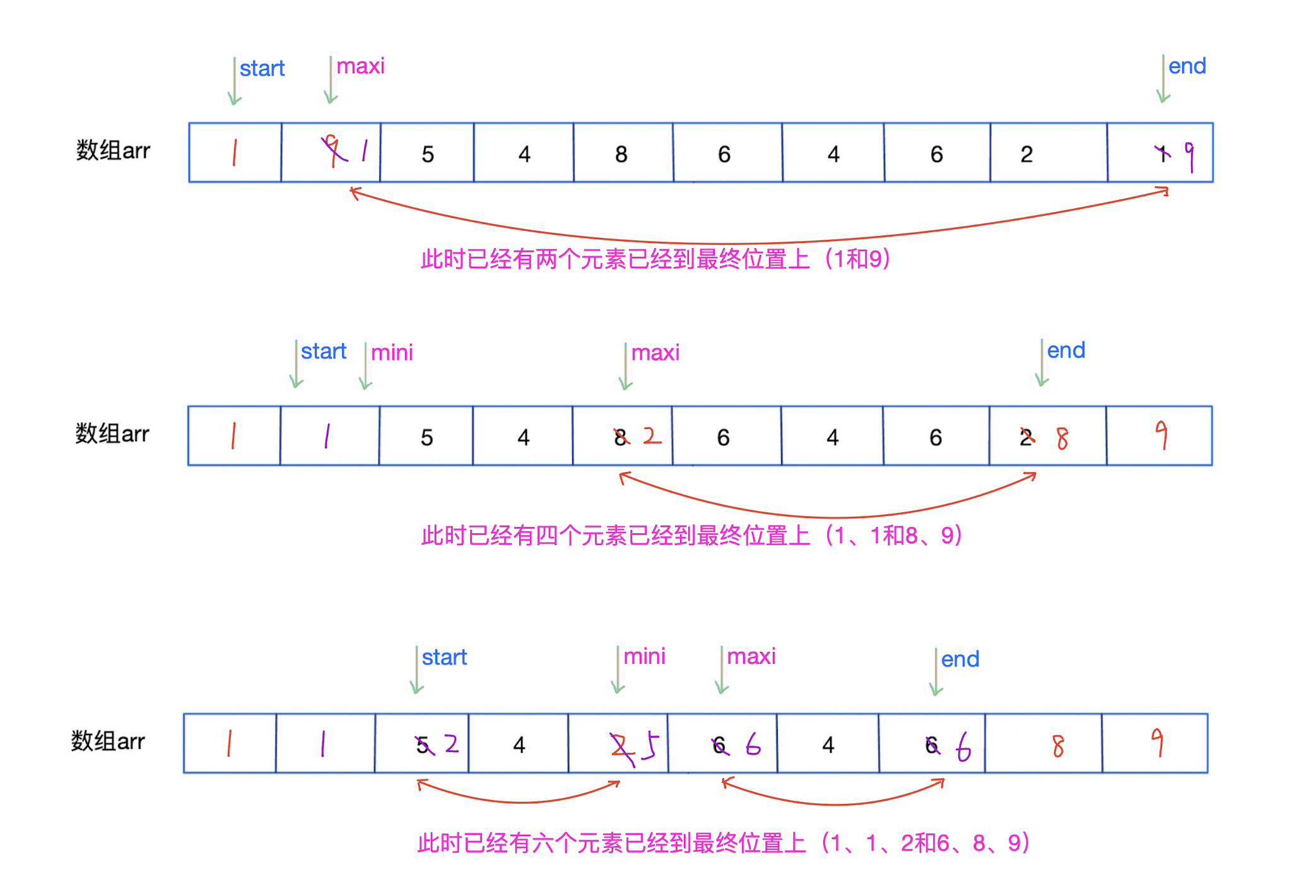
- 这里仅演示部分过程,其他过程自行考虑(和上述过程类似)。
-
以此类推,直到所有元素均排序完毕。
4.3、排序代码
-
使用
mini和maxi分别记录当前未排序的最小值下标和最大值下标在未排序的序列中找出最小值和最大值,然后分别交换到当前未排序的起始位置和末尾位置。需要注意的是:如果当前未排序的序列中,最大值刚好在未排序序列的起始位置,那么就需要记录好这个最大值与当前未排序的序列中的最小值交换后的位置,不记录的话,那么当前maxi指向的值不一定是最大值!//选择排序 void SelectSort(int *arr, int n) {int mini = 0;int maxi = 0;int start = 0;int end = n - 1;while (start < end) {for (int i = start + 1; i <= end; ++i) {if (arr[i] > arr[maxi]) {maxi = i;}if (arr[i] < arr[mini]) {mini = i;}}Swap(&arr[mini], &arr[start]);//注意此时如果start刚好是最大值的话,就会把最大值换走了,也就是本来最大值在 0 位置,交换后换到其他位置了,所以判断一下if (start == maxi) {maxi = mini;//找到最大值的下标}Swap(&arr[maxi], &arr[end]);//向中间靠拢++start;--end;} } -
时间复杂度计算:对于选择排序排序来说,没有什么最坏时间复杂度和最好时间复杂度,因为不管原数组起始是升序还是降序,元素之间的比较次数都是一样的:
- 确定了2个元素的最终位置:
n-1 - 确定了4个元素的最终位置:
n-1+n-3 - 确定了6个元素的最终位置:
n-1+n-3+n-5 - …
- 确定了n个元素的最终位置:
n+n-3+n-5+...+1 = n*(n+1)/4 <---大约,所以时间复杂度为O(n^2)。
- 确定了2个元素的最终位置:
-
空间复杂度计算:由于没有开辟额外空间来辅助数组排序,故空间复杂度为O(1)。
-
算法稳定性:不稳定,考虑序列(1,2,2),排序后序列为(1,2,2),我们发现
2的相对位置发生了变化,所以是不稳定的排序算法。
5、堆排序
堆排序详解
6、快速排序
快速排序递归方法和非递归方法详解
7、归并排序
快速排序递归方法和非递归方法详解
8、计数排序
8.1、算法思想
-
计数排序就是使用一个临时数组来记录这个原数组的元素对应这个临时数组下标出现的次数,然后再对这个临时数组从
0开始往后按下标出现的次数遍历。 -
优化:对于原数组最小值较大的情况,我们可以使用对这个临时数组进行==重定位==。
-
重定位:相当于计算机组成原理里面的将逻辑地址转化为物理地址的过程,比如序列
110,110,111,120,125,122,115,118,112,118,其实它的范围就是在110~125,区间长度为16,如果我们按照这个序列的最大值来建立数组,那么需要长度为126的数组,但是这个数组的前110个空间都是0,也就是并没有用上,浪费了。但是如果创建一个长度为16的数组,下标为0~15(原数组每个元素减110,这个110是这个原数组的最小值),是不是就可以匹配这个序列的范围了呢?那么问题是之后遍历这个临时数组,只能得到
0~15的下标,并不是我们要的110~125!其实,在遍历这个临时数组的时候,可以继续使用重定位,把这个0~15的下标重定位到110~125(每个下标都加110,这个110是这个原数组的最小值)!
-

8.2、排序过程图解
-
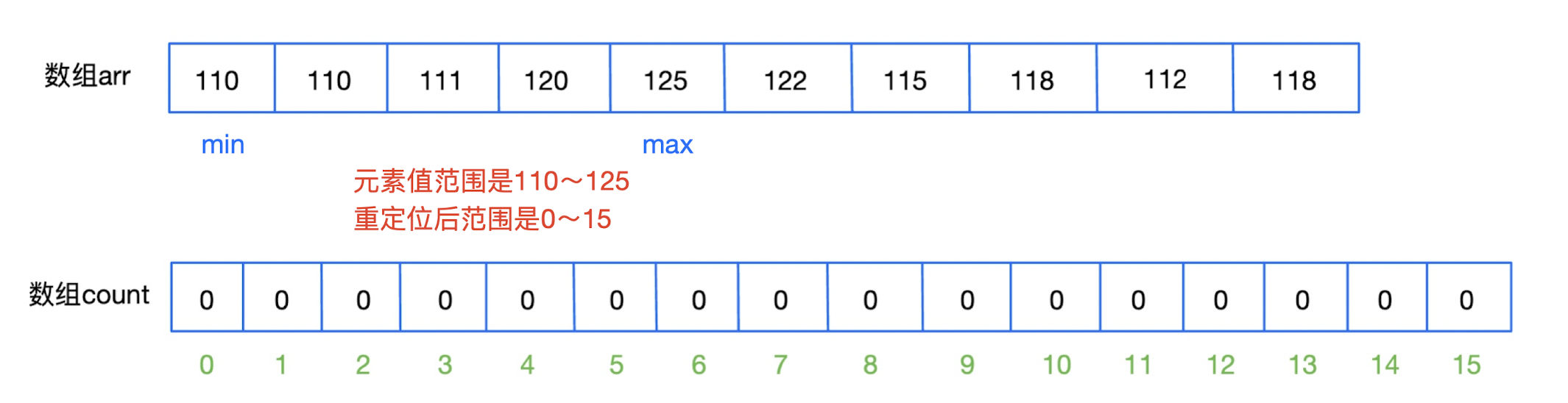
先找到原数组的最大值和最小值,然后就可以确定临时数组的长度,然后初始化这个临时数组(全
0)。
-
然后依次遍历原数组,根据重定位,将原数组的元素减去最小值去对应临时数组的下标,并对这个下标里的元素
+1。
-
遍历这个临时数组,对每个下标进行遍历,按下标对应的元素值看需要对此下标遍历几次(需要重定位回去—加上原数组的最小值)。

8.3、排序代码
-
用
min和max记录原数组的最小值和最大值,确定临时数组的长度(max-min+1),然后对临时数组count进行初始化,接下来就是把原数组里的元素重定位为临时数组的下标(元素值减原数组的最小值),并对此下标对应的元素+1,一直到遍历完原数组。 -
遍历这个临时数组
count,对每个下标进行遍历,按下标对应的元素值看需要对此下标遍历几次(需要重定位回去—加上原数组的最小值)。 -
注意:这里不能找最大最小值的下标,因为在重定位回去的时候
arr[j++]在变,也就是最小值下标不一定对应到最小值了!//计数排序 void CountSort(int *arr, int n) {//先找出数组的最大最小值int max = arr[0];int min = arr[0];for (int i = 1; i < n; ++i) {if (arr[i] > max) {max = arr[i];}if (arr[i] < min) {min = arr[i];}}//节省空间,需要对元素重定位int capacity = max - min + 1;//元素大小区间//记录每个元素的出现次数int *count = (int *) malloc(sizeof(int) * capacity);if (count == NULL) {perror("malloc error");exit(-1);}memset(count, 0, sizeof(int) * capacity);for (int i = 0; i < n; ++i) {count[arr[i] - min]++;}int j = 0;for (int i = 0; i < capacity; ++i) {while (count[i]--) {arr[j++] = i + min;}}free(count); } -
时间复杂度计算:这里找最大值最小值花费时间
n,遍历临时数组花费时间k(临时数组长度),所以时间复杂度为O(n+k)。 -
空间复杂度计算:使用了临时数组(临时数组长度为k),所以空间复杂度为O(k)。
-
算法稳定性:稳定,因为它是利用一个数据的索引来记录元素出现的次数,而这个数组的索引就是元素的数值。当计数排序完成后,具有相同数值的元素在数组中的位置也相同,因此它们的顺序保持不变。
八大排序算法整体的时间复杂度、空间复杂度、算法稳定性等看如下表格:
排序算法 平均时间复杂度 最好情况 最坏情况 空间复杂度 排序方式 稳定性 (直接)插入排序 O(n^2) O(n) O(n^2) O(1) 内部排序 稳定 希尔排序 O(n^1.3) O(n^1.3) O(n^1.3) O(1) 内部排序 不稳定 冒泡排序 O(n^2) O(n) O(n^2) O(1) 内部排序 稳定 (简单)选择排序 O(n^2) O(n^2) O(n^2) O(1) 内部排序 不稳定 堆排序 O(nlogn) O(nlogn) O(nlogn) O(1) 内部排序 不稳定 快速排序 O(nlogn) O(nlogn) O(n^2) O(logn) 内部排序 不稳定 归并排序 O(nlogn) O(nlogn) O(nlogn) O(n) 外部排序 稳定 计数排序 O(n+k) O(n+k) O(n+k) O(k) 外部排序 稳定
OKOK,八大排序算法就到这里。如果你对Linux和C++也感兴趣的话,可以看看我的主页哦。下面是我的github主页,里面记录了我的学习代码和leetcode的一些题的题解,有兴趣的可以看看。
Xpccccc的github主页
相关文章:

八大排序算法(含时间复杂度、空间复杂度、算法稳定性)
文章目录 八大排序算法(含时间复杂度、空间复杂度、算法稳定性)1、(直接)插入排序1.1、算法思想1.2、排序过程图解1.3、排序代码 2、希尔排序3、冒泡排序3.1、算法思想3.2、排序过程图解3.3、排序代码 4、(简单)选择排序4.1、算法…...
【C++】:引用的概念/引用的特性/常引用/引用的使用场景/传值与传引用的效率比较/引用和指针的区别/内联函数的概念/内联函数的特性
引用的概念 引用不是新定义一个变量,而是给已存在变量取了一个别名,编译器不会为引用变量开辟内存空间,它和它引用的变量共用同一块内存空间 比如:李逵,在家称为"铁牛",江湖上人称"黑旋风&…...
点云地面点提取——基于格网算法)
Python点云处理(十七)点云地面点提取——基于格网算法
目录 0 简述1 算法流程2 优缺点3 实现4 效果5 结语0 简述 提取地面点是点云数据分析和处理中的重要任务,而点云格网法是一种常用的地面点提取方法。点云格网法(Grid-based Method),通过将点云数据划分为网格单元,根据高程值分析来实现地面点的提取。 1 算法流程 步骤1:…...

Flink 中kafka broker缩容导致Task一直重启
背景 Flink版本 1.12.2 Kafka 客户端 2.4.1 在公司的Flink平台运行了一个读Kafka计算DAU的流程序,由于公司Kafka的缩容,直接导致了该程序一直在重启,重启了一个小时都还没恢复(具体的所容操作是下掉了四台kafka broker࿰…...

纯前端js中使用sheetjs导出excel,并且合并标题
先定义变量----用的是Vue2 ,以下在vue的data:{}中定义--------------//空格占位符 headerTopTitle: [患者信息, , , , , , , , , 入出院信息, , , , , , , 病案首页中的出院主要诊断, ,出院其他诊断(病案首页中原始信息), , , , ,…...

猫眼 校园招聘_1面
(1)打包和构建工具 vite 和 webpack 功能 1. 构建原理: Webpack 是一个静态模块打包器,通过对项目中的JavaScript、css、Image 等文件进行分析,生成对应的静态资源,并且通过一些插件和加载器来实现各种功…...
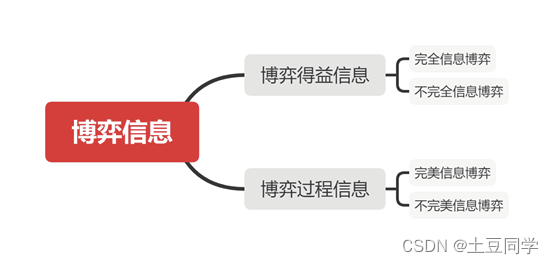
博弈论——博弈信息结构
博弈信息结构 0 引言 在一个博弈构成中,博弈信息结构是不可或缺要素。博弈信息,顾名思义,就是在博弈中,博弈方对于信息的了解。知己知彼,百战不殆。和短兵相接的战争一样,只有充分了解自己的优劣势&#x…...
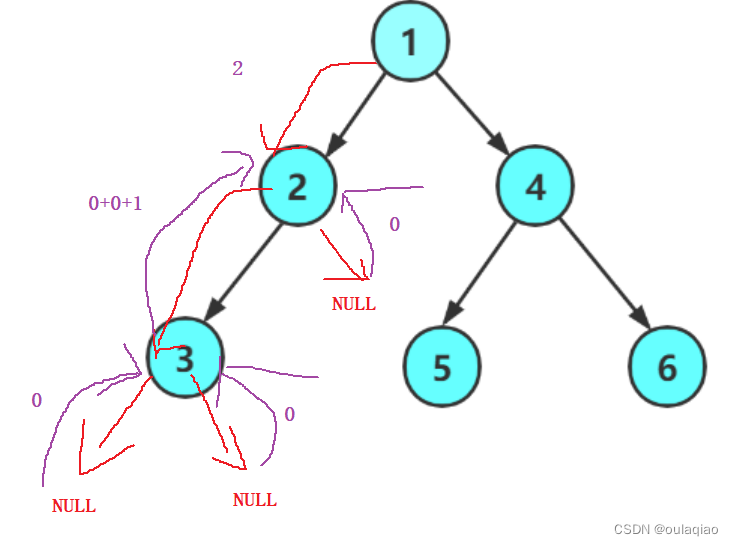
求二叉树的高度——函数递归的思想
二叉树的高度:左右两个数最高的那个的1 int TreeHight(BTNode* root) {if (root NULL){return 0;}int lefhightTreeHight(root->left);int righthight TreeHight(root->right);return lefhight > righthight ? TreeHight(root->left) 1 : TreeHight…...
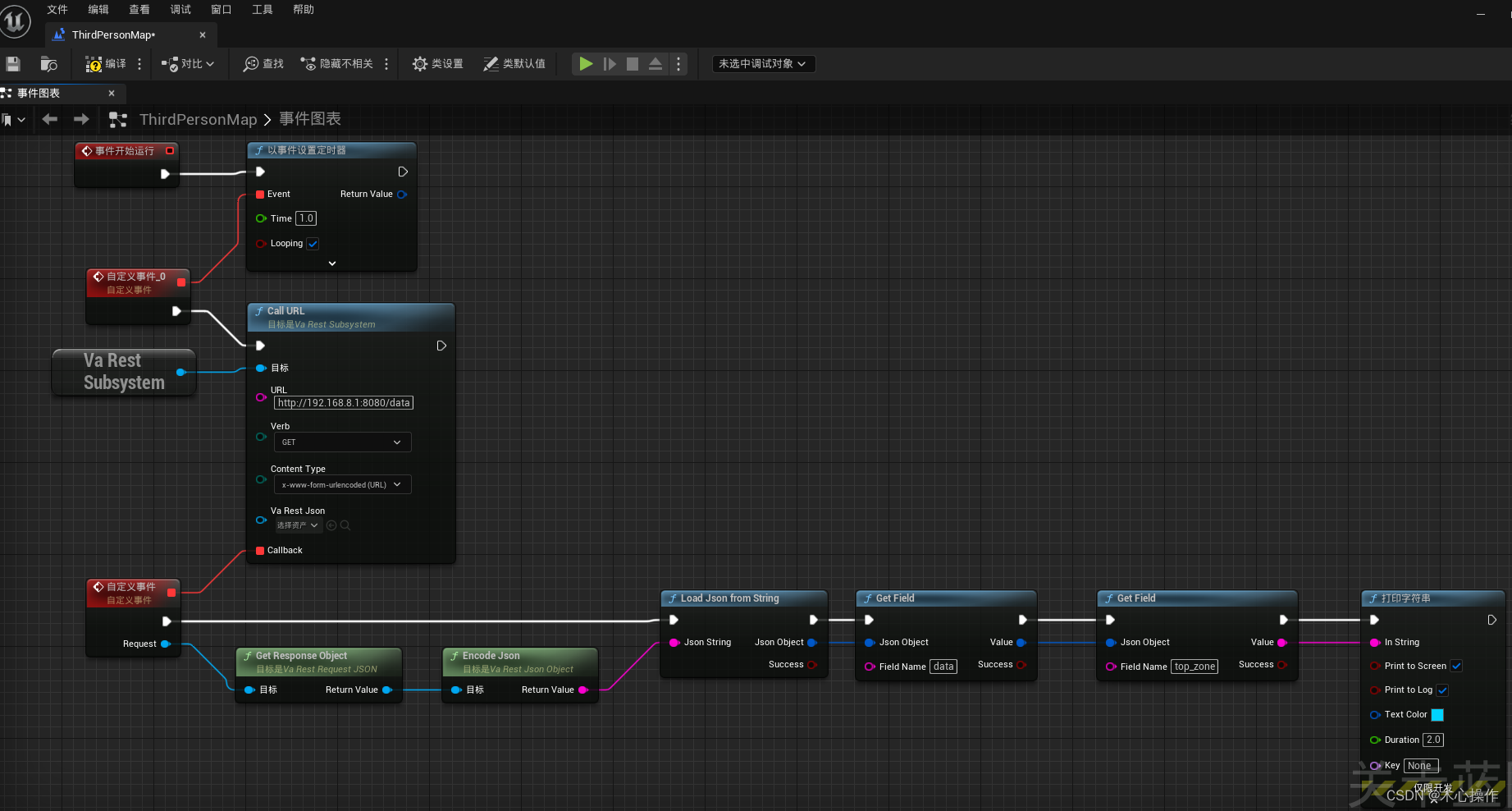
ue5蓝图请求接口
安装与使用 1、在虚幻商城搜索 VaRest 插件 2、选择自己项目的对应版本安装 3、查看是否安装成功 4、进入项目后,分别启动VaRest、JSON Blueprint Utilities两个插件(勾选后会提示重启项目) 5、基本用法:打开关卡蓝图使用…...
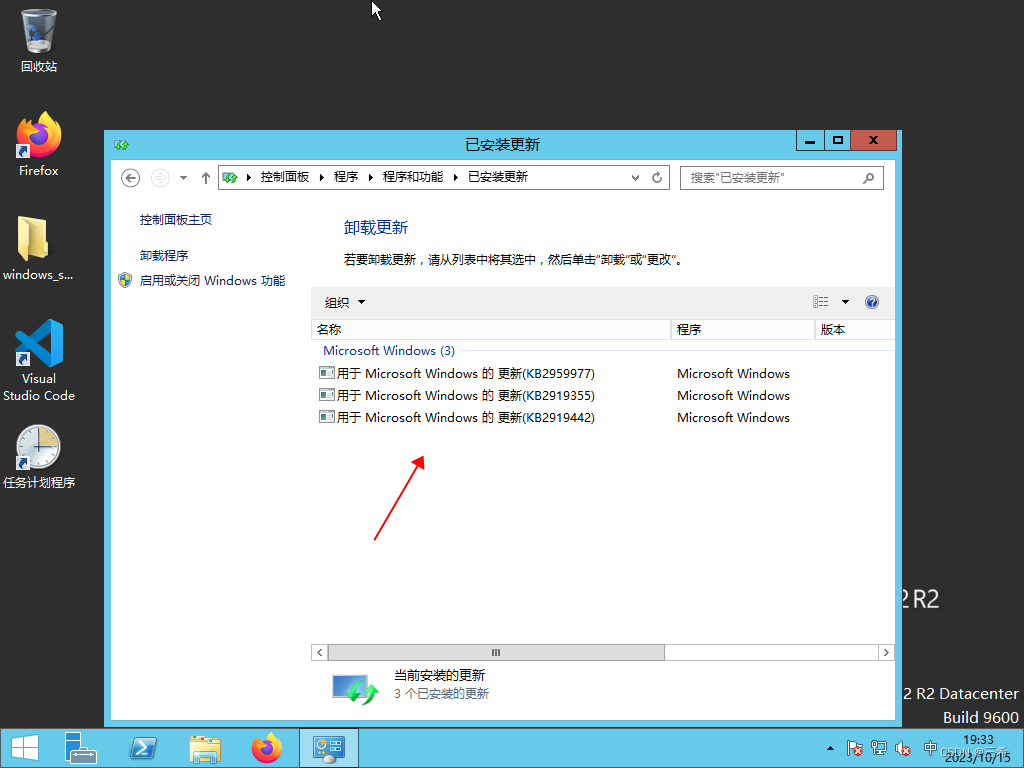
windows server 2012 查看已打了哪些补丁
打开控制面板 点击卸载程序 点击 查看已安装的更新 下图是已安装的补丁...

参加CSP-J第一轮后的感受
本人现在初二。作为一名学了4年多c的人,我一直都挺想考过CSP。于是,去年我就去考了。 当时初一,感觉自己实力不够,就只报了J组的。果不其然,63分,没过。 经过1年的苦练,今年又去考了。 J组78分&…...

rust 智能指针
智能指针 Box Box 的使用场景 由于 Box 是简单的封装,除了将值存储在堆上外,并没有其它性能上的损耗。而性能和功能往往是鱼和熊掌,因此 Box 相比其它智能指针,功能较为单一,可以在以下场景中使用它: 特…...
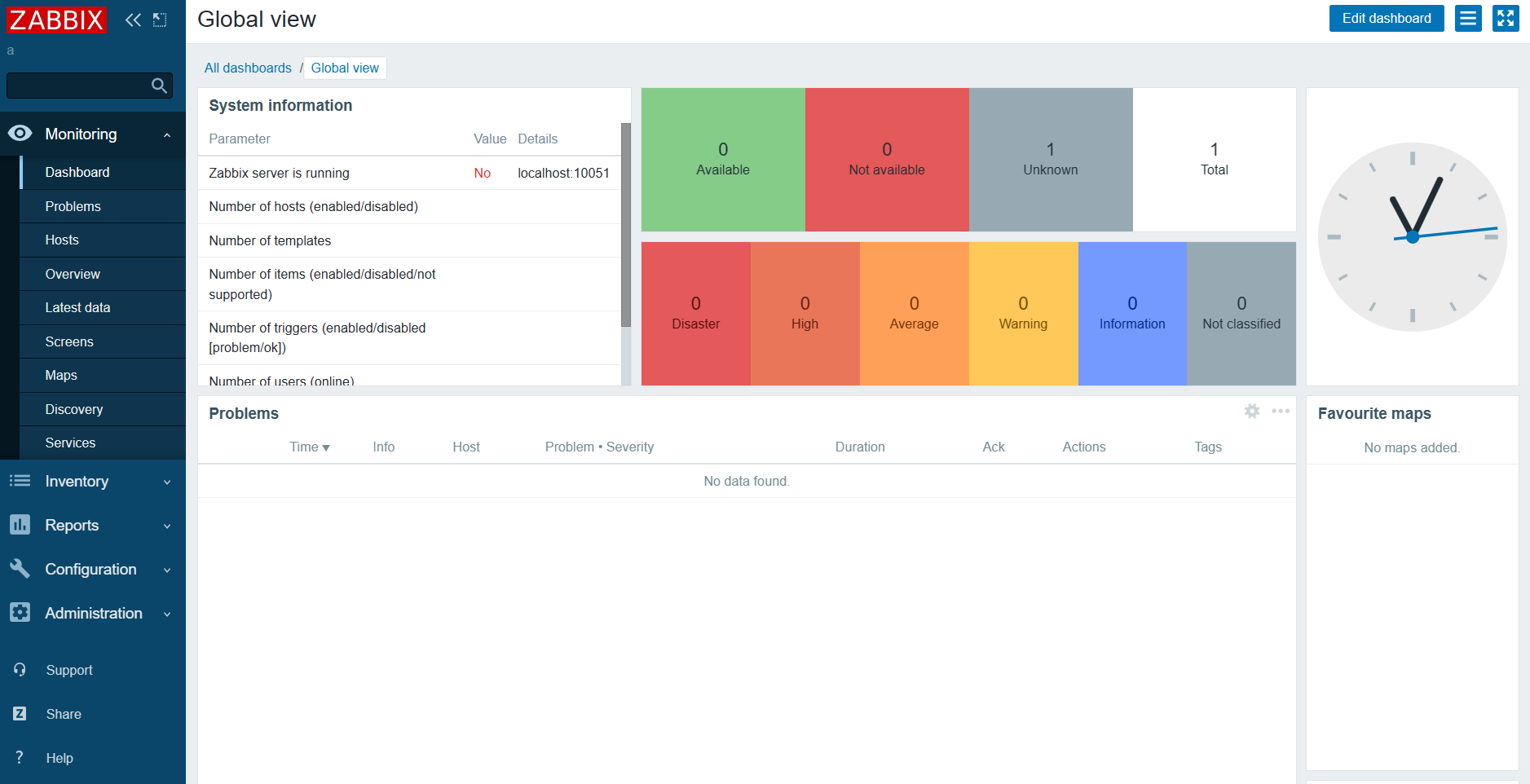
CentOS 7系统安装配置Zabbix 5.0LTS 步骤
目录 一、查看Zabbix官方教程(重点) 二、安装 Docker 创建 Mysql 容器 安装 Docker 依赖包 添加 Docker 官方仓库 安装 Docker 引擎 启动 Docker 服务并设置开机自启 验证 Docker 是否成功安装 拉取 MySQL 镜像 查看本地镜像 运行容器 停止和启…...

【学习之路】Multi Agent Reinforcement Learning框架与代码
【学习之路】Multi Agent Reiforcement Learning框架与代码 Introduction 国庆期间,有个客户找我写个代码,是强化学习相关的,但我没学过,心里那是一个慌,不过好在经过详细的调研以及自身的实力,最后还是解…...
)
android 13.0 SystemUI导航栏添加虚拟按键功能(二)
1.概述 在13.0的系统产品开发中,对于在SystemUI的原生系统中默认只有三键导航,想添加其他虚拟按键就需要先在构建导航栏的相关布局 中分析结构,然后添加相关的图标xml就可以了,然后添加对应的点击事件,就可以了,接下来先分析第二步关于导航栏的相关布局情况 然后实现功能…...
-- Stream的中间操作)
Java8 新特性之Stream(二)-- Stream的中间操作
目录 1.filter(Predicate) 2.map(Function) 3.flatMap(Function) 4.distinct() 5.sorted([Comparator]) 6.limit(n) 7.skip(n) 8.peek(Consumer)...
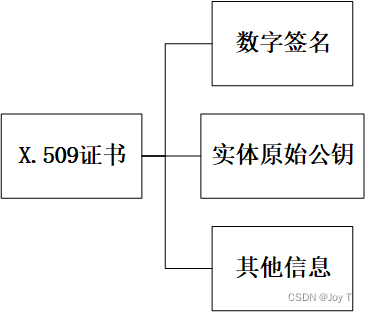
CA与区块链之数字签名详解
CA与区块链验证本质上都是数字签名,首先,我们看一下什么是数字签名! 数字签名 数字签名是公钥密码学中的一种技术,用于验证信息的完整性和发送者的身份。简而言之,数字签名是一种确认信息来源和信息完整性的手段。它通…...

一文解读如何应用 REST 对资源进行访问?
文章目录 一、REST 简介二、涉及注解2.1 RequestMapping2.2 PathVariable2.3 RestController2.4 GetMapping、PostMapping、PutMapping、DeleteMapping补充:PathVariable、RequestBody、RequestParam 区别与应用 三、REST风格案例 一、REST 简介 REST (Representat…...

使用JAVA发送邮件
这里用java代码编写发送邮件我采用jar包,需要先点击这里下载三个jar包:这三个包分别为:additionnal.jar;activation.jar;mail.jar。这三个包缺一不可,如果少添加或未添加均会报下面这个错误: C…...
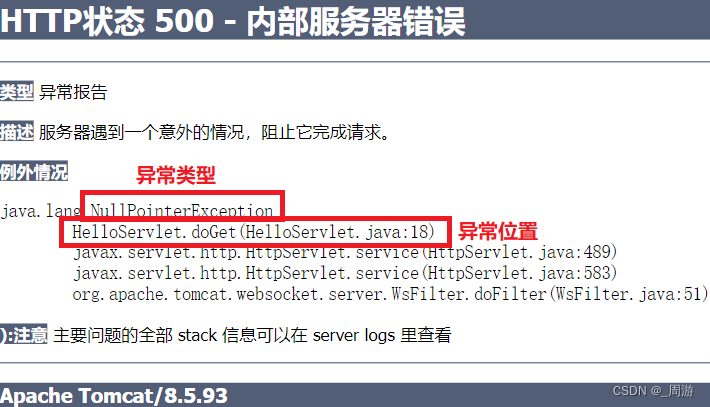
【JavaEE】_servlet程序的编写方法
目录 1. 创建项目 2. 引入依赖 3. 创建目录结构 3.1 在main目录下创建一个webapp目录 3.2 在webapp目录下创建一个WEB-INF目录 3.3 在WEB-INF目录下创建一个web.xml文件 3.4 在web.xml中进行代码编写 4. 编写代码 4.1 在java目录下创建类 4.2 打印"hello world&…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...
