数据结构 - 5(二叉树7000字详解)
一:二叉树的基本概念
1.1树形结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。


注意:树形结构中,子树之间不能有交集,否则就不是树形结构
1.2 数的相关概念

- 结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为6
- 树的度:一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为6
- 叶子结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I…等节点为叶结点
- 双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
- 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
- 根结点:一棵树中,没有双亲结点的结点;如上图:A
- 结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
- 树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
树的以下概念只需了解,在看书时只要知道是什么意思即可:
- 非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G…等节点为分支结点
- 兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
- 堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
- 结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
- 子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
- 森林:由m(m>=0)棵互不相交的树组成的集合称为森林
1.3 树的表现形式
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,如:双亲表示法,孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
class Node {int value; // 树中存储的数据Node firstChild; // 第一个孩子引用Node nextBrother; // 下一个兄弟引用
}

1.4树的应用
文件系统管理(目录和文件)


1.5 二叉树
二叉树是一种常见的树状数据结构,它由节点和边组成。每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树具有以下特点:
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
如下图所示:

注意:对于任意的二叉树都是由以下几种情况复合而成的:

大自然的奇观:


1.6 两种特殊的二叉树
-
满二叉树:满二叉树是指每个节点都有两个子节点(除了叶子节点)。换句话说,满二叉树是一种节点数目达到最大可能值的二叉树。例如,如果一棵二叉树的深度为d,那么它的节点数目就是2^d - 1。
-
完全二叉树:完全二叉树是指除了最后一层外,其他层的节点都被完全填充,并且最后一层的节点都尽量靠左排列的二叉树。换句话说,完全二叉树是在满二叉树的基础上,去掉一些叶子节点而得到的二叉树。
如图所示:

1.7 二叉树的重要性质
- 性质一:叶子结点的个数是度为2结点的个数+1
要理解为什么对任何一棵二叉树,其叶结点个数为 n0,度为2的非叶结点个数为 n2,有 n0 = n2 + 1,我们首先需要了解二叉树的定义和性质。
二叉树是一种特殊的树结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。叶节点是没有子节点的节点,而度为2的非叶节点是具有两个子节点的非叶节点。
让我们来证明这个等式 n0 = n2 + 1 :
-
首先,我们将二叉树的节点按照度的数量进行分类。由于二叉树的节点度数只有0、1、2三种情况,我们可以得出以下等式:n = n0 + n1 + n2,其中 n 表示二叉树的总节点数。
-
其次,我们来考虑度为0的节点,也就是叶节点。叶节点是没有子节点的节点,所以它的度为0。假设叶节点的个数为 n0。
-
然后,我们考虑度为2的非叶节点,也就是具有两个子节点的非叶节点。假设度为2的非叶节点的个数为 n2。
-
根据二叉树的性质,每个非叶节点都会有两个子节点。所以,度为2的非叶节点的总子节点个数为 2 * n2。
-
接下来,我们来看看二叉树的总子节点个数。根据节点分类的等式,可以得出总子节点个数为 n1 + 2 * n2。其中 n1 表示度为1的节点的个数。
-
由于每个节点都有两个子节点,所以总子节点个数应该等于 n - 1(根节点除外)。因此,我们可以得到以下等式:n1 + 2 * n2 = n - 1。
-
最后,我们将以上的等式整合起来,得到 n0 + n1 + n2 = n。将 n1 + 2 * n2 = n - 1 代入其中,得到 n0 + (n - 1) = n,即 n0 = n2 + 1。
根据上述推导,我们可以得出结论:对于任何一棵二叉树,其叶结点个数为 n0,度为2的非叶结点个数为 n2,有 n0 = n2 + 1。即叶子结点的个数是度为2结点的个数+1,这是二叉树性质的一个重要结论。
-
性质二:具有n个结点的完全二叉树的深度k为 上取整
-
性质三:对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若2i+1<n,左孩子序号:2i+1,否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,否则无右孩子

- 性质四:我们可以根据array.length-2)>>1计算倒数第一个非叶子节点的索引
二:二叉树的遍历,存储和实现
2.1 二叉树的遍历
二叉树的遍历方式有四种,分别是前序遍历,中序遍历,后序遍历和层序遍历,这是我们约定俗成的规定。
前序遍历(Preorder Traversal)是一种遍历二叉树的方法。在前序遍历中,我们首先访问根节点,然后遍历左子树,最后遍历右子树。具体过程如下:
- 访问当前节点(根节点)。
- 递归地前序遍历左子树。
- 递归地前序遍历右子树。
下面是一个例子来说明前序遍历:
1/ \2 3/ \4 5
前序遍历结果:1 2 4 5 3
中序遍历(Inorder Traversal)是另一种遍历二叉树的方法。在中序遍历中,我们首先遍历左子树,然后访问根节点,最后遍历右子树。具体过程如下:
- 递归地中序遍历左子树。
- 访问当前节点(根节点)。
- 递归地中序遍历右子树。
下面是一个例子来说明中序遍历:
1/ \2 3/ \4 5
中序遍历结果:4 2 5 1 3
后序遍历(Postorder Traversal)是另一种遍历二叉树的方法。在后序遍历中,我们首先遍历左子树,然后遍历右子树,最后访问根节点。具体过程如下:
- 递归地后序遍历左子树。
- 递归地后序遍历右子树。
- 访问当前节点(根节点)。
下面是一个例子来说明后序遍历:
1/ \2 3/ \4 5
后序遍历结果:4 5 2 3 1
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。

这个图的层序遍历结果就是ABCDEFGHI
下面是一个练习,请同学们根据下图,给出以下二叉树的四种遍历方式:
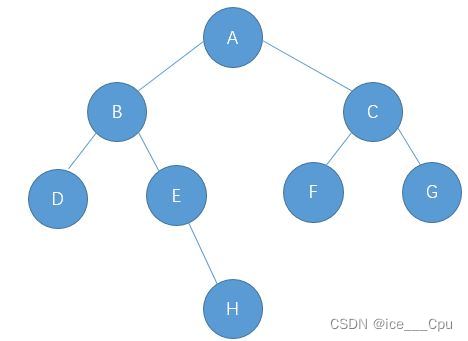
前序遍历:ABDEHCFG
中序遍历:DBEHAFCG
后序遍历:DHEBFGCA
层序遍历:ABCDEFGH
2.2二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。顺序存储在下节介绍。
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式,具体如下:
// 孩子表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}// 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点
}
本文采用孩子表示法来构建二叉树。
2.3二叉树的实现
在Java中,并没有内置的二叉树类。但是,我们可以通过自定义类来实现二叉树的功能。下面是模拟实现二叉树并给出主方法进行测试的代码:
import java.util.LinkedList;
import java.util.Queue;// 定义二叉树节点类
class Node {int data;Node left;Node right;// 节点构造函数public Node(int data) {this.data = data;left = null;right = null;}
}// 定义二叉树类
class BinaryTree {Node root;// 构造函数,初始化根节点public BinaryTree() {root = null;}// 获取树中节点的个数public int size(Node root) {if (root == null) {return 0;} else {// 递归地计算左子树和右子树节点个数,并加上根节点return 1 + size(root.left) + size(root.right);}}// 获取叶子节点的个数public int getLeafNodeCount(Node root) {if (root == null) {return 0;} else if (root.left == null && root.right == null) {// 叶子节点的定义:左右子节点都为空return 1;} else {// 递归地计算左子树和右子树叶子节点个数,并相加return getLeafNodeCount(root.left) + getLeafNodeCount(root.right);}}// 获取第K层节点的个数public int getKLevelNodeCount(Node root, int k) {if (root == null || k <= 0) {return 0;} else if (k == 1) {// 第1层就是根节点本身return 1;} else {// 递归地计算左子树和右子树第k-1层节点个数,并相加return getKLevelNodeCount(root.left, k - 1) + getKLevelNodeCount(root.right, k - 1);}}// 获取二叉树的高度public int getHeight(Node root) {if (root == null) {return 0;} else {// 递归地计算左子树和右子树的高度,并取最大值,再加上根节点int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return Math.max(leftHeight, rightHeight) + 1;}}// 检测值为value的元素是否存在public Node find(Node root, int val) {if (root == null) {return null;} else if (root.data == val) {// 找到了与目标值相等的节点return root;} else {// 递归地在左子树和右子树中查找值为val的节点Node foundNode = find(root.left, val);if (foundNode == null) {foundNode = find(root.right, val);}return foundNode;}}// 层序遍历public void levelOrder(Node root) {if (root == null) {return;}// 使用队列辅助层序遍历Queue<Node> queue = new LinkedList<>();queue.add(root);while (!queue.isEmpty()) {Node current = queue.poll();System.out.print(current.data + " ");if (current.left != null) {queue.add(current.left);}if (current.right != null) {queue.add(current.right);}}}// 判断一棵树是不是完全二叉树public boolean isCompleteTree(Node root) {if (root == null) {return true;}Queue<Node> queue = new LinkedList<>();boolean isNonFullNodeFound = false; // 是否找到了不是满节点的节点queue.add(root);while (!queue.isEmpty()) {Node current = queue.poll();if (current.left != null) {if (isNonFullNodeFound) {return false; // 如果之前找到了不是满节点的节点,当前节点有左子节点,则不是完全二叉树}queue.add(current.left);} else {isNonFullNodeFound = true; // 记录找到了不是满节点的节点}if (current.right != null) {if (isNonFullNodeFound) {return false; // 如果之前找到了不是满节点的节点,当前节点有右子节点,则不是完全二叉树}queue.add(current.right);} else {isNonFullNodeFound = true; // 记录找到了不是满节点的节点}}return true;}
}下面再给出主方法用于测试这些方法的功能:
import java.util.Arrays;public class Main {public static void main(String[] args) {// 创建一个示例二叉树Node root = new Node(1);root.left = new Node(2);root.right = new Node(3);root.left.left = new Node(4);root.left.right = new Node(5);root.right.left = new Node(6);root.right.right = new Node(7);BinaryTree binaryTree = new BinaryTree();// 测试 size 方法System.out.println("树中节点的个数:" + binaryTree.size(root)); // 7// 测试 getLeafNodeCount 方法System.out.println("叶子节点的个数:" + binaryTree.getLeafNodeCount(root)); // 4// 测试 getKLevelNodeCount 方法int k = 3;System.out.println("第" + k + "层节点的个数:" + binaryTree.getKLevelNodeCount(root, k)); // 2// 测试 getHeight 方法System.out.println("二叉树的高度:" + binaryTree.getHeight(root)); // 3// 测试 find 方法int target = 5;Node foundNode = binaryTree.find(root, target);if (foundNode != null) {System.out.println("找到值为" + target + "的节点");} else {System.out.println("未找到值为" + target + "的节点");}// 测试 levelOrder 方法System.out.print("层序遍历结果:");binaryTree.levelOrder(root); // 1 2 3 4 5 6 7System.out.println();// 测试 isCompleteTree 方法System.out.print("是否是完全二叉树:");if (binaryTree.isCompleteTree(root)) {System.out.println("是");} else {System.out.println("否");}}
}
相关文章:

数据结构 - 5(二叉树7000字详解)
一:二叉树的基本概念 1.1树形结构 树是一种非线性的数据结构,它是由n(n>0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 注意&am…...
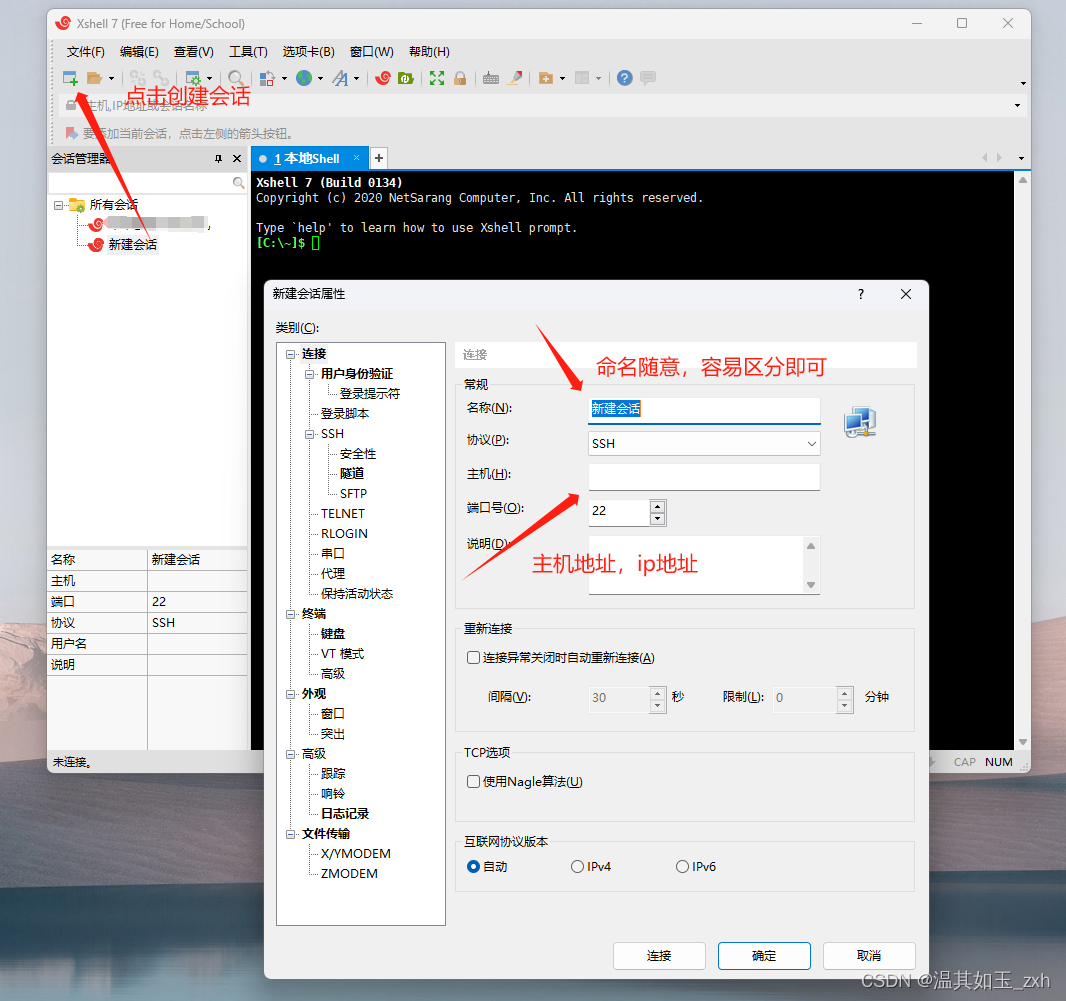
xshell使用方法(超详细)
一、安装 下载最新版安装即可,不需要做任何配置。 安装完成后输入账号名和邮箱,确认后邮箱会收到一条确认邮件,将里面的链接点开即可免费使用(仅安装后会出现,认证后以后再打开不需要重复操作,如果重新安…...
【数据库系统概论】第三章关系数据库标准语言SQL
选择题会考: 1.数据查询: SELECT:用于选择需要查询的列和行。 FROM:用于指定要查询的表。 WHERE:用于指定查询条件。 GROUP BY:用于按照指定的列对结果进行分组。 HAVING:用于指定分组条件…...

云计算是什么?学习云计算能做什么工作?
很多人经常会问云计算是什么?云计算能干什么?学习云计算能做什么工作?其实我们有很多人并不知道云计算是什么,小知今天来给大家讲讲学习云计算能做什么。 中国的云计算行业目前正处于快速发展阶段,随着互联网和数字化…...
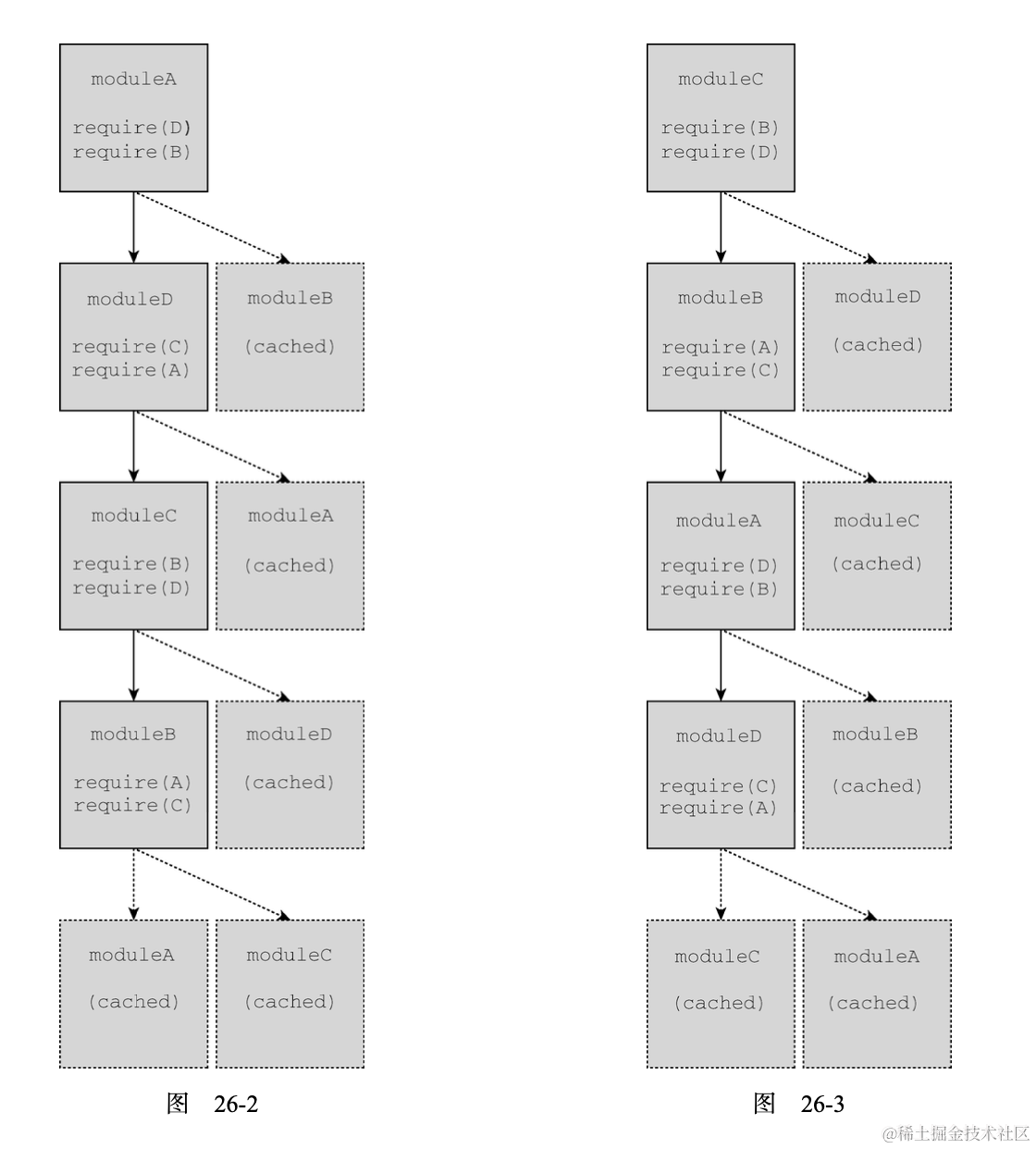
ES6 -- 模块化(CommonJS、AMD、ES Module)
模块模式 将代码拆分成独立的块,然后再将这些块连接起来可以通过模块模式来实现。这种模式背后的思想很简单:把逻辑分块,各自封装,相互独立,每个块自行决定对外暴露什么,同时自行决定引入执行哪些外部代码…...
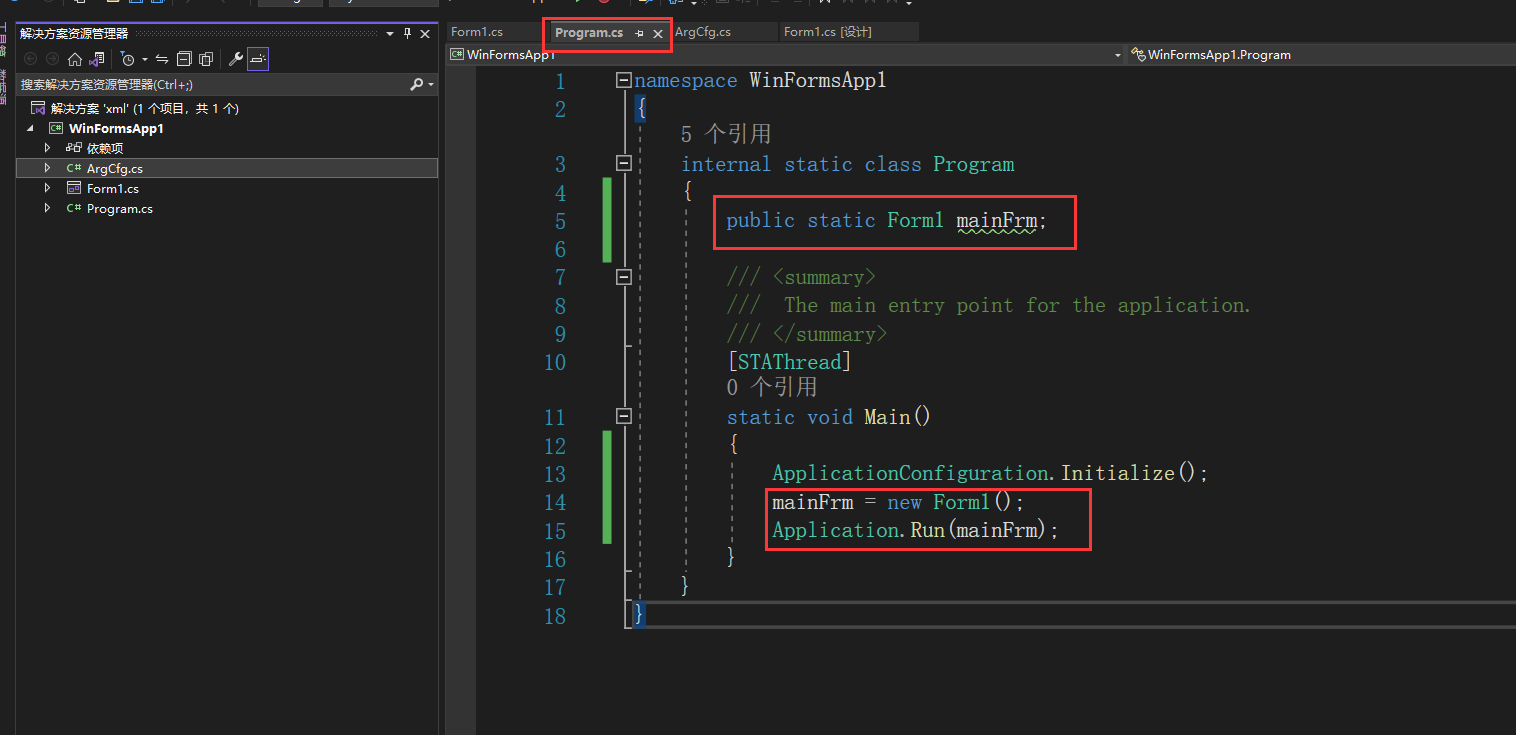
c# xml 参数读取读取的简单使用
完整使用之测试参数的读取(xml) 保存一个xml文档(如果没有就会生成一个默认的 里面的参数用的是我们默认设置的),之后每次更改里面的某项,然后保存 类似于重新刷新一遍。 这里所用的xml测试参数前面需要加…...

gym原来是这样用的
今天down了一个深度强化学习的程序,但是试来试去总是跑不成功,第一句就出问题了 env gym.make("clusterEnv-v0").unwrapped总是报没有该环境,思想半天,然后发现这是自己写的环境,需要到gym中去注册才能使用…...

百度SEO优化技巧与布局(提升网站排名的5种有效方法)
网站SEO关键词介绍: SEO(SearchEngineOptimization)即搜索引擎优化,是通过一系列技术手段和策略,让网站在搜索引擎中获得更好的排名和流量。关键词是SEO优化的重要组成部分,通过关键词布局合理,…...
文案配音软件哪个好?(适合新手使用)
随着短视频的逐渐普及,视频博主越来越多,所以很多朋友也期待成为视频博主。但是,如果你想成为一个有名的视频博主,你需要在很多层面上比别人做得更好。其中之一就是视频文字的配音。相信大部分人都没有配音的技巧,所以…...

excel映射xml方法
excel映射xml方法 创建xml模板 新建一个文本文件,编写模板并命名为xxx.xml <?xml version"1.0" encoding"UTF-8"?> <root><item ID""><surname></surname><man></man><woman>&…...
2023/10/15
文章目录 1.uniapp之Vue2升Vue3值得注意的几点1.1 页面生命周期的使用1.2 引入资源的方式 2. 浏览器本地存储之Cookie和webStorage3. CSS变量 var()的用法4. CSS之实现线性渐变背景5. 图片无法和文字对齐的正确解决方案6. 使用正则处理接口返回的富文本内的图片7. transition实…...

Linux系统中如何开启和配置OpenGauss数据库的远程连接
文章目录 前言1. Linux 安装 openGauss2. Linux 安装cpolar3. 创建openGauss主节点端口号公网地址4. 远程连接openGauss5. 固定连接TCP公网地址6. 固定地址连接测试 前言 openGauss是一款开源关系型数据库管理系统,采用木兰宽松许可证v2发行。openGauss内核深度融合…...

【Docker】Docker网络及容器间通信详解
目录 背景 默认网络 1、bridge 网络模式 2、host 网络模式 3、none 网络模式 4、container 网络模式 自定义网络 容器间网络通信 IP通信 Docker DNS server Joined容器 前言 本实验通过docker DNS server和joined 容器两种方法实现Docker容器间的通信。Docker容器间…...
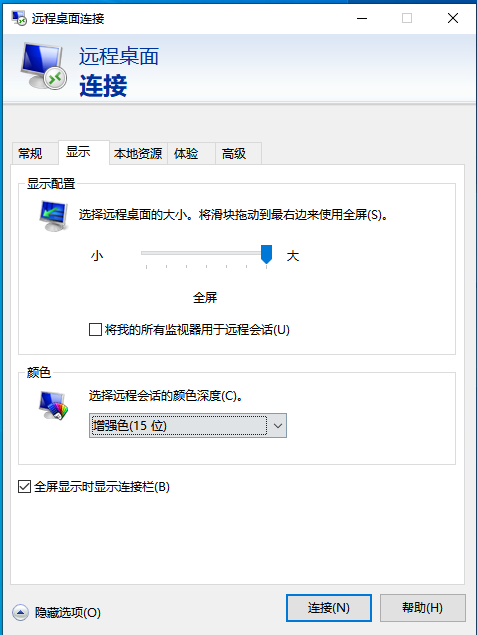
TikTok国际版 使用特网科技Bluestacks模拟器安装方法
特网科技Bluestacks模拟器主机 桌面自带Bluestacks模拟器 TikTok国际版Bluestacks模拟器搜索tiktot 登录google应用商店-安装TikTok 安装过程可能需要3-5分钟不等-配置过低可能会导致安装失败,建议升级更高内存。 安装完成-打开 安装成功APP-我的游戏查看 打开国际版…...
【Hello Algorithm】暴力递归到动态规划(四)
动态规划的数组压缩技巧 - 机器人走格子问题 题目是leetcode62题目原题 表示如下 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中…...

arm day 8
arm 写一段按键中断代码 main.c #include "uart.h" #include "key_it.h" int main() {char c;char *s;uart4_init();//串口初始化//中断初始化key_it_config();while(1){//保证主程序不结束}return 0; } src/key_it.c #include"key_it.h"voi…...
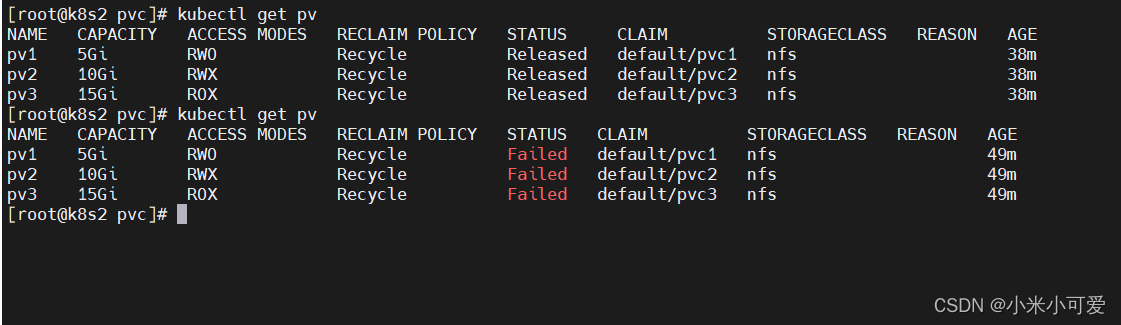
k8s-14 存储之volumes
Volumes配置管理 容器中的文件在磁盘上是临时存放的,这给容器中运行的特殊应用程序带来一些问题。首先,当容器崩溃时,kubelet 将重新启动容器,容器中的文件将会丢失因为容器会以干净的状态重建。其次,当在一个 Pod 中…...
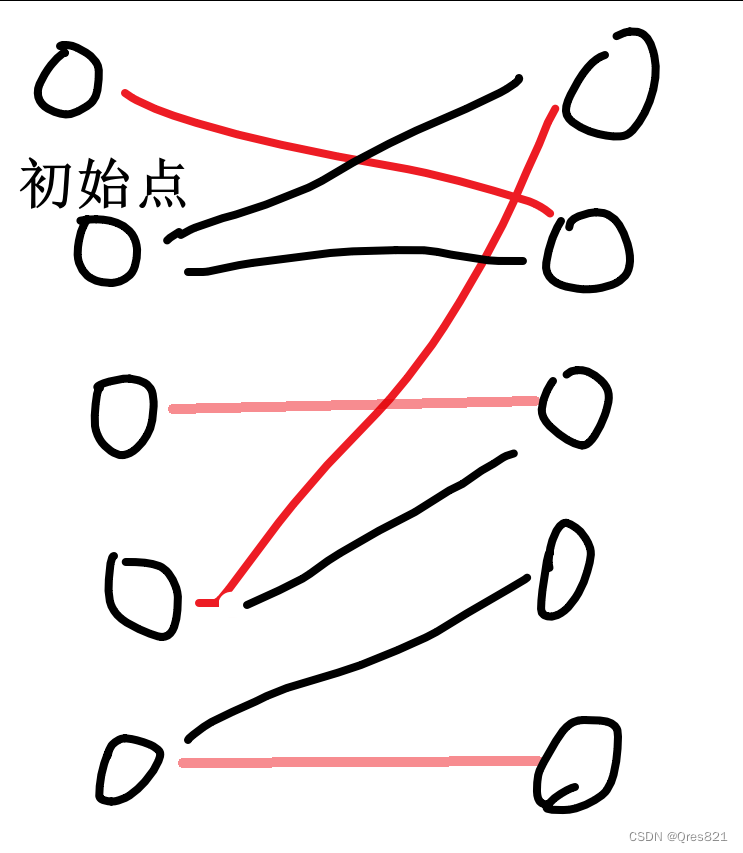
二分图博弈
一张二分图,Alice和Bob每人走一步,不能重复走,谁不能走谁输 结论:若存在最大匹配不包含初始点,则Bob赢,否则Alice赢 以上图为例,红色为最大匹配。 首先对于Alice第一步只能走黑边。而Alice无论…...

【C++】C++11—— 包装器
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:C学习 🎯长路漫漫浩浩,万事皆有期待 上一篇博客:【C】C11…...

LED显示屏高刷新率和低刷新率有什么区别
LED显示屏的刷新率是指图像在LED显示屏上更新的速度,也即屏幕上的图像每秒钟出现的次数,它的单位是赫兹(Hz)。LED显示屏的刷新率越高,图像闪烁感就越小,稳定性也就越高,换言之对视力的保护也越好…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
