Java基础——了解进制和位运算
文章目录
- 关于进制
- 位运算
- 左位移
- 右位移
- 无符号右移
- 取反
- 按位与
- 按位或
- 按位异或
关于进制
所有数字在计算机底层都是以二进制的形式存在。
进制的四种表达形式:
- 二进制:[0,1],满2进1,以0b或0B开头。
- 八进制:[0-7],满8进1,以0开头。
- 十进制:[0-9],满10进1。
- 十六进制:[0,9,A-F],满16进1,以0x或0X开头(此处的A-F不区分大小写)。
进制之间的相互换算参考:https://xinzhi.wenda.so.com/a/1537180588200142
在Java中的整数,默认是int类型占4字节,占32bit(1字节等于8bit),其第32位是符号位;long类型占8个字节,占64bit,其第64位是符号位。
比如:int整数8的二进制:00000000 00000000 00000000 00001000,最多不超过32位。
注意:符号位,0表示正,1表示负。
二进制整数的三种形式:
- 原码:直接将一个整数转换二进制数,最高位是符号位。
- 反码:正数的反码和原码相同,负数的反码是对原码符号位以外的每一位按位取反(由于是负数的反码所以符号位总是1)。
- 补码:正数的补码和原码相同,负数的补码是它的反码加1。
注意:正数的原码、反码和补码都相同。补码转原码是补码取反+1
为什么要使用原码、反码和补码的表示形式?
答:计算机辨别“符号位”会让计算机的基础电路设计变得复杂,于是人们想到将符号位也参与运算,我们知道根据运算法则,减去一个整数等于加上一个负数,所以机器可以只有加法没有减法,这样计算机运算的设计就简单了。(在计算机中,都是补码参与计算)
为什么正数的原码、反码和补码相同?
答:反码和补码的出现是用来解决做减法问题,通过加负数的方式达到做减法的效果,所以只有负数才有反码和补码,正数没有,所有正数的反码和补码都是本身(原码)。
例:演示在计算机中如何计算1+(-1)= 0的过程
整数二进制转换:
1:00000000 00000000 00000000 00000001
-1:10000000 00000000 00000000 00000001
补码转换:
1:00000000 00000000 00000000 00000001(补码)
-1:11111111 11111111 11111111 11111110(反码)-> 11111111 11111111 11111111 11111111(补码)
说明:二进制相加,逢二进一。00000000 00000000 00000000 00000001+ 11111111 11111111 11111111 11111111----------------------------------------100000000 00000000 00000000 00000000 -> 00000000 00000000 00000000 00000000 = 0注:最高位超出位数直接被舍弃,最后计算结果为0.
位运算
位运算是对补码的操作。运算完后,需要将补码转回原码再转十进制,才是最后运算结果,由于正数的补码和原码相同,就不需要转,负数需要转。
注意:
- 正数位运算,不管左位移还是右位移,都是补0。
- 负数位运算,左位移和无符号右移补0,且左位移最高位总是1,右位移补1。
左位移
运算符:<<
说明:整数的二进制数向左移动指定位数。
示例:1 << 2 = 4
补码转换:
1:00000000 00000000 00000000 000000011向左位移2位(1<<2)00000000 00000000 00000000 00000001
<< 00000000 00000000 00000000 00000001----------------------------------------00000000 00000000 00000000 00000100 = 4
注:左位移后,左边超出部分舍弃,右边用0补齐。
右位移
运算符:>>
说明:整数的二进制数向右位移指定位数。
示例:8>>2 = 2
补码转换:
8:00000000 00000000 00000000 00001000
-8:10000000 00000000 00000000 00001000 (取反)-> 11111111 11111111 11111111 11110111 (+1)-> 11111111 11111111 11111111 111110008向右位移2位00000000 00000000 00000000 00001000
>> 00000000 00000000 00000000 00001000------------------------------------------0000000000 00000000 00000000 000010 = 2
注:右位移后,左边用0补齐,右边超出部分舍弃。-8向右位移2位11111111 11111111 11111111 11111000
>> 11111111 11111111 11111111 11111000------------------------------------------11111111 11111111 11111111 11111110 (取反)-> 10000000 00000000 00000000 00000001 (+1)-> 10000000 00000000 00000000 00000010 = -2
注:运算后得到的是补码需转成原码。
无符号右移
运算符:>>>
说明:整数的二进制数向右位移指定位数,正数用0补齐,负数用1补齐。
示例:
8>>>2 = 2
-8>>>2 = 1073741822
补码转换:
8:00000000 00000000 00000000 00001000
-8:10000000 00000000 00000000 00001000 (取反)-> 11111111 11111111 11111111 11110111 (+1)-> 11111111 11111111 11111111 111110008无符号向右位移2位00000000 00000000 00000000 00001000
>>> 00000000 00000000 00000000 00001000------------------------------------------0000000000 00000000 00000000 000010 = 2-8无符号向右位移2位11111111 11111111 11111111 11111000
>>> 11111111 11111111 11111111 11111000------------------------------------------00111111 11111111 11111111 11111110 = 1073741822
注:无符号右位移,左边用0补齐,右边超出部分舍弃。
在线二进制转换十进制:https://www.jisuan.mobi/KZn.html
取反
运算符:~
运算规则:~1=0; ~0=1,1变0,0变1。
示例:~3 = -4
补码转换:
3:00000000 00000000 00000000 000000113取反
~ 00000000 00000000 00000000 00000011
-------------------------------------11111111 11111111 11111111 11111100 (取反)-> 10000000 00000000 00000000 00000011 (+1)-> 10000000 00000000 00000000 00000100 = -4
按位与
运算符:&
运算规则:0&0=0; 0&1=0; 1&0=0; 1&1=1,只有同时都是1的时候才是1,否则是0。
示例:3 & 5 = 1
补码转换:
3:00000000 00000000 00000000 00000011
5:00000000 00000000 00000000 000001013按位与500000000 00000000 00000000 00000011
& 00000000 00000000 00000000 00000101
-------------------------------------00000000 00000000 00000000 00000001 = 1
按位或
运算符:|
运算规则:0 | 0=0; 0 | 1=1; 1 | 0=1; 1 | 1=1,任意一方是1就是1,否则是0。
示例:3 | 5 = 7
补码转换:
3:00000000 00000000 00000000 00000011
5:00000000 00000000 00000000 000001013按位或500000000 00000000 00000000 00000011
| 00000000 00000000 00000000 00000101
-------------------------------------00000000 00000000 00000000 00000111 = 7
按位异或
运算符:^
运算规则:0^0=0; 0^1=1; 1^0=1; 1^1=0,相同的值为0,不同的值为1。
示例:3^5 = 6
补码转换:
3:00000000 00000000 00000000 00000011
5:00000000 00000000 00000000 000001013按位异或500000000 00000000 00000000 00000011
^ 00000000 00000000 00000000 00000101
---------------------------------------00000000 00000000 00000000 00000110 = 6
相关文章:

Java基础——了解进制和位运算
文章目录 关于进制位运算左位移右位移无符号右移取反按位与按位或按位异或 关于进制 所有数字在计算机底层都是以二进制的形式存在。 进制的四种表达形式: 二进制:[0,1],满2进1,以0b或0B开头。八进制:[0-7]…...

mybatisplus 自定义mapper加多表联查结合分页插件查询时出现缺失数据的问题
问题描述 最近做项目时使用了mybatisplus,分页插件也使用的是mybatisplus自带的分页插件,业务需求是查询客户列表,每个客户列表中有一个子列表,在通过分页插件查询后,会出现数量总数为子列表总数、客户列表与子列表不…...
陪诊系统|陪诊软件革新陪诊体验解决病患难题
随着医疗服务的不断升级和改善,陪诊系统作为现代医院的一项重要创新,为病患和陪护人员提供了更加便捷、高效的服务体验。本文将全面介绍陪诊系统的功能、特点和优势,让您更好地了解和体验这一创新科技。 一、系统功能 陪诊系统旨在为病患和陪…...

[Tkinter 教程08] Canvas 图形绘制
python - [译][Tkinter 教程08] Canvas 图形绘制 - 个人文章 - SegmentFault 思否 一、简介 Canvas 为 Tkinter 提供了绘图功能. 其提供的图形组件包括 线形, 圆形, 图片, 甚至其他控件. Canvas 控件为绘制图形图表, 编辑图形, 自定义控件提供了可能. 在第一个例子里, …...

ES6 Symbol 数据结构
1. Symbol概念以及引入原因 ES6 引入了的一种新的原始数据类型Symbol,表示独一无二的值。它是 JavaScript 语言的第七种数据类型,前六种是:undefined、null、布尔值(Boolean)、字符串(String)、…...

Redis常用数据类型、Redis常用命令
Redis常用数据类型、Redis常用命令: Redis常用数据类型:1. 字符串String 类型2. 哈希hash 类型3. 列表list 类型4. 集合set 类型5. 有序集合sorted set / zset 类型 Redis常用命令:1. 字符串操作命令2. 哈希操作命令3. 列表操作命令4. 集合操…...
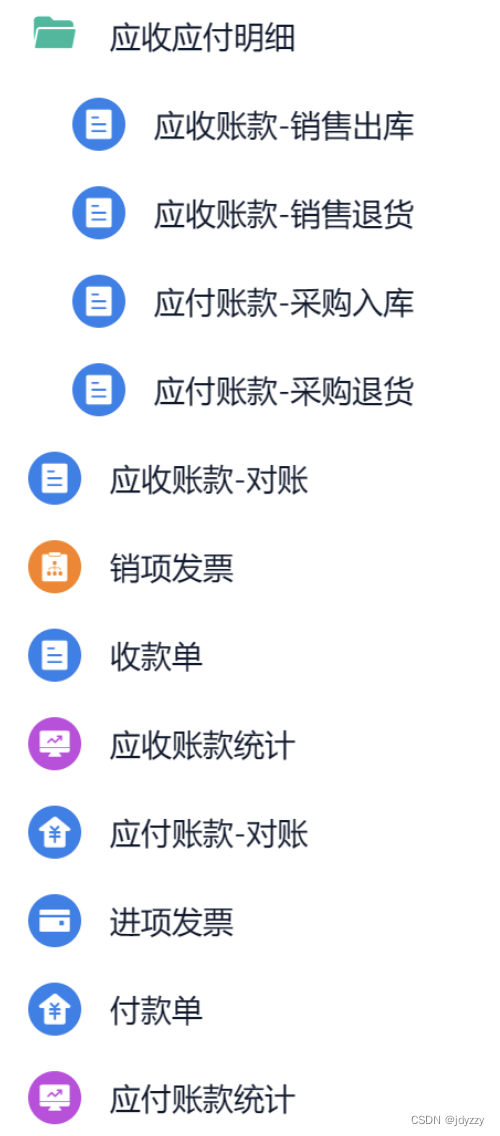
ERP系统是如何运作的?erp管理系统操作流程
ERP系统是如何运作的?ERP系统的运作流程是怎样的? 以简道云ERP管理系统为例: 各行各业适配的ERP系统>>>>https://www.jiandaoyun.com 可以看到上面那个流程图,一般来说,我们把ERP系统可以分为4个大的模…...
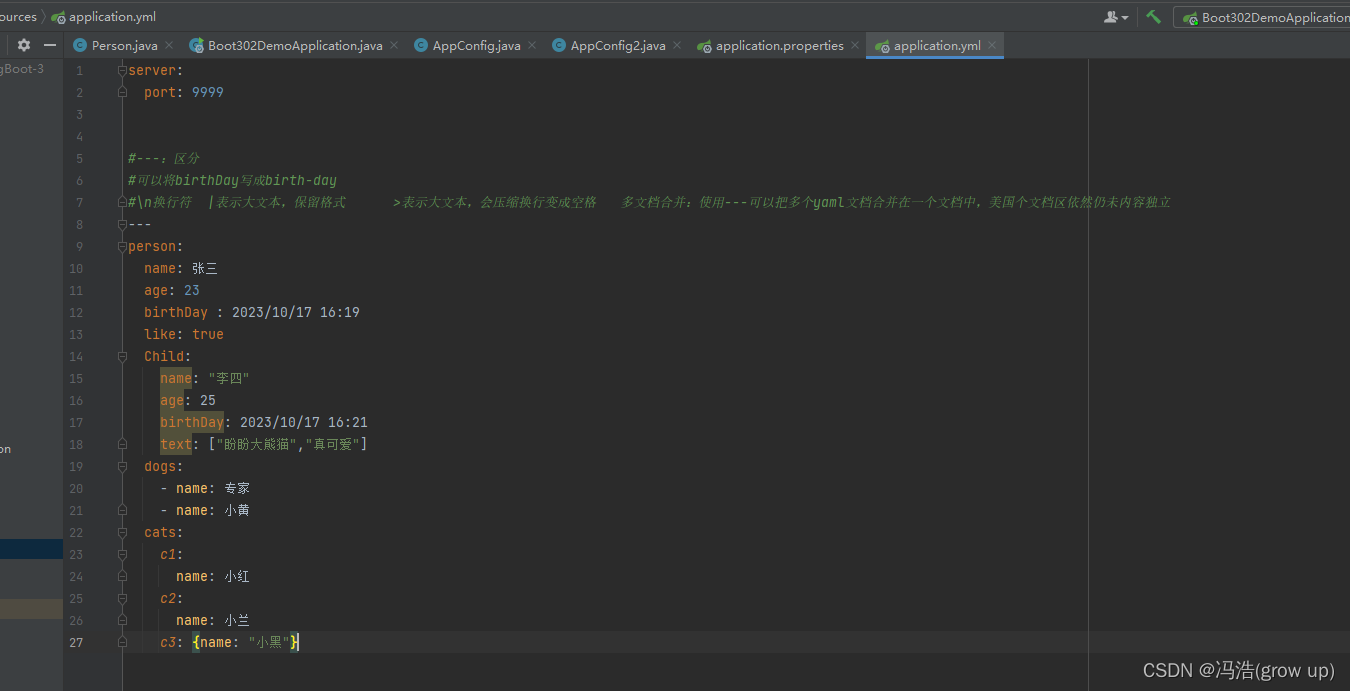
springBoot复杂对象表示和lombok的使用
springBoot复杂对象表示 前言简单案例lombok的使用通过properties文件进行绑定在yaml文件中使用 前言 对象:键值对的集合,如:映射(map)/哈希(hash)/字典(dictionary) 数组:一组按次…...
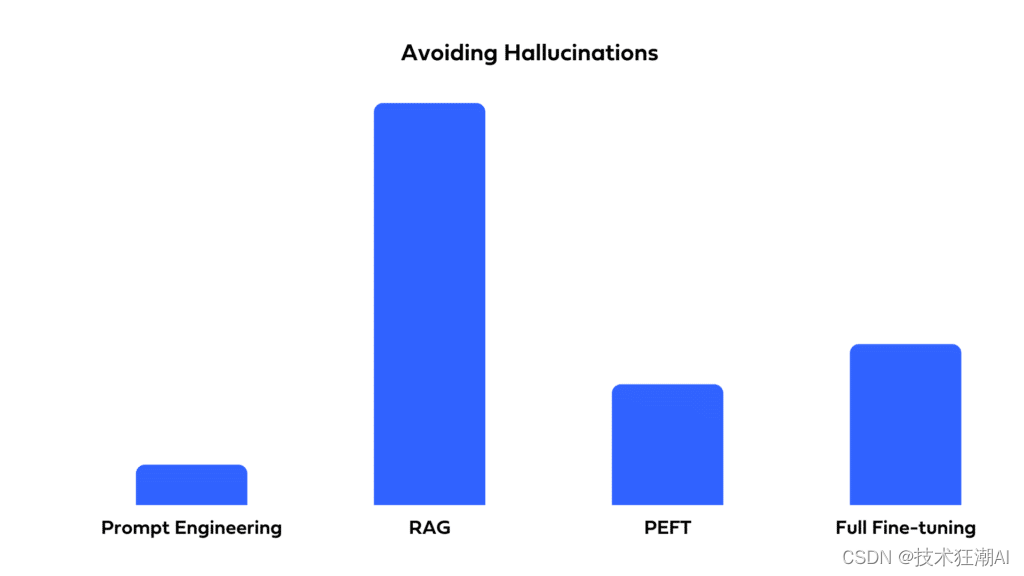
如何选择最适合你的LLM优化方法:全面微调、PEFT、提示工程和RAG对比分析
一、前言 自从ChatGPT问世以来,全球各地的企业都迫切希望利用大型语言模型(LLMs)来提升他们的产品和运营。虽然LLMs具有巨大的潜力,但存在一个问题:即使是最强大的预训练LLM也可能无法直接满足你的特定需求。其原因如…...
)
Jenkins实现CI/CD发布(Ansible/jenkins共享库/gitlab)
Jenkins实现多环境发布 1. 需求介绍 本人负责公司前端业务模块,由于前端模块较多,所以在编写jenkinsfile时会出现很多项目使用的大部分代码相同的情况,为解决这种问题,采用了jenkins的共享库方式优化,并且jenkins要支持…...

使用navicat查看类型颜色
问题描述: 最近遇到一个mongodb的数据问题。 在date日期数据中,混入了string类型的数据,导致查询视图报错: $add only supports numeric or date types解决办法: 使用类型颜色工具。 找到在last_modified_date字段中…...

iOS 中,Atomic 修饰 NSString、 NSArray,也会线程不安全
众所周知,基础类型如 int、float 的变量被 atomic 修饰后就具有原子性,则线程安全。 然而有些情况,atomic 修饰后不一定是线程安全的。 atomic 修饰 NSString,NSArray 的时候,只是保障首地址(数组名&…...

2023医药微信公众号排名榜top100汇总合集
相信每个医药人都或多或少关注了几个医药微信公众号,便于日常了解到最新的医药新闻包括治疗技术、药物研发、研究成果、医学进展、临床试验进展、市场动向等前沿动态。 笔者也不列外,大大小小的公众号收集了有上百个,本着方便查看的目的&…...

基于YOLO算法的单目相机2D测量(工件尺寸和物体尺寸)三
1.简介 1.1 2D测量技术 基于单目相机的2D测量技术在许多领域中具有重要的背景和意义。 工业制造:在工业制造过程中,精确测量是确保产品质量和一致性的关键。基于单目相机的2D测量技术可以用于检测和测量零件尺寸、位置、形状等参数,进而实…...

Cython编译文件出错
报错信息: (rpc) stuamax:~/segment/dss_crf$ python setup.py install Compiling pydensecrf/eigen.pyx because it changed. Compiling pydensecrf/densecrf.pyx because it changed. [1/2] Cythonizing pydensecrf/densecrf.pyx /home/stu/anaconda3/envs/rpc/l…...

WPF 用户控件依赖注入赋值
前言 我一直想组件化得去开发WPF,因为我觉得将复杂问题简单化是最好的 如何组件化开发 主窗口引用 <Window x:Class"WpfApp1.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.…...
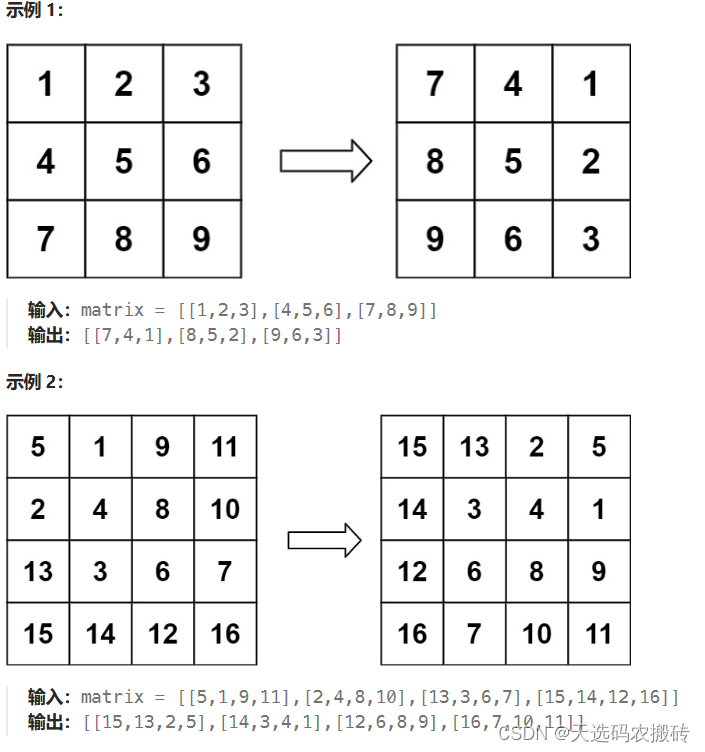
leetcode-48.旋转图像
1. 题目 leetcode题目链接 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。 2. 编程 矩阵转置: 遍历矩阵&#x…...
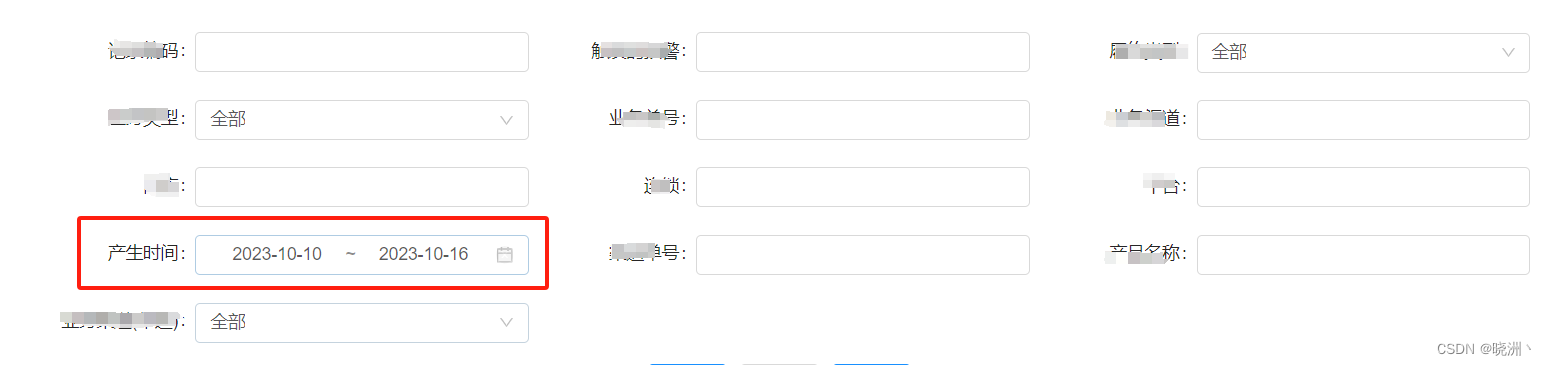
antd的RangePicker设置默认值,默认近七天(andt+react)
import moment from "moment";state {initData:[moment().startOf(day).subtract(6, d), moment().endOf(day)], }<FormItem label"产生时间" {...tailItemLayout}>{getFieldDecorator("produceTime", {initialValue: initData})(<Ran…...
大数据可视化模块竞赛Vue项目文件结构与注意事项
1.vue项目src目录下只有两个文件夹与两个js文件,如图所示: 2.asseets目录存放包或其他外部资料 注意 :echarts采用的是引用外部文件导入 let echarts = require(@/assets/echarts.min.js) 3.components目录存放绘制页面的vue文件(我这里示例创建了一个newPage.vue)…...
户外运动盛行,运动品牌如何利用软文推广脱颖而出?
全民健康意识的提升和城市居民对亲近自然的渴望带来户外运动的盛行,这也使运动品牌的市场保持强劲发展势头,那么在激烈的市场竞争中,运动品牌应该如何脱颖而出呢?下面就让媒介盒子告诉你! 一、 分享户外运动干货 用户…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
