AtCoder abc130
F题提交了无数遍,最后发现是三分求解的写法错了
C - Rectangle Cutting
盲猜都在xy的中心点时可以无限分割,否则不能
D - Enough Array
前缀和二分求位置
E - Common Subsequence
公共子序列求有几种组合
设 d p [ i ] [ j ] dp[i][j] dp[i][j]代表s取到i t取到j时的序列数
当s[i]!=t[j] 时
d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + d p [ i ] [ j − 1 ] − d p [ i − 1 ] [ j − 1 ] dp[i][j]=dp[i-1] [j] + dp[i][j - 1] - dp[i - 1][j - 1] dp[i][j]=dp[i−1][j]+dp[i][j−1]−dp[i−1][j−1]
因为 d p [ i ] [ j ] dp[i][j] dp[i][j]可以视作为 d p [ i − 1 ] [ j ] dp[i - 1][j] dp[i−1][j]添上s[i]后总的序列数
d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]是 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]添上t[j]的序列数
另一边 d p [ i ] [ j − 1 ] dp[i][j - 1] dp[i][j−1]也将 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]包含在内,因此计算了两次 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]需要减去
当s[i]==t[j]时, d p [ i ] [ j ] dp[i][j] dp[i][j]在 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]的序列上各增加一个长度,因此在刚才的计算后再加上 d p [ i − 1 ] [ j − 1 ] dp[i-1][j-1] dp[i−1][j−1]
# -*- coding: utf-8 -*-
# @time : 2023/6/2 13:30
# @author : yhdu@tongwoo.cn
# @desc :
# @file : atcoder.py
# @software : PyCharm
import bisect
import copy
import sys
from sortedcontainers import SortedList
from collections import defaultdict, Counter, deque
from functools import lru_cache, cmp_to_key
import heapq
import math
sys.setrecursionlimit(100010)mod = 10 ** 9 + 7def main():items = sys.version.split()if items[0] == '3.10.6':fp = open("in.txt")else:fp = sys.stdinn, m = map(int, fp.readline().split())s = list(map(int, fp.readline().split()))t = list(map(int, fp.readline().split()))dp = [[0] * (m + 1) for _ in range(n + 1)]for i in range(n + 1):dp[i][0] = 1for i in range(m + 1):dp[0][i] = 1for i in range(1, n + 1):for j in range(1, m + 1):if s[i - 1] == t[j - 1]:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]else:dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1]dp[i][j] %= modprint(dp[n][m])if __name__ == "__main__":main()F - Minimum Bounding Box
max-min显然是凸函数(忘了证明方法),暴力三分可以过
还有一种不那么暴力的解法:
不需要维护所有的x y
只需要维护向上、向下的y中最大值与最小值
向左向右x最大值与最小值
# -*- coding: utf-8 -*-
# @time : 2023/6/2 13:30
# @author : yhdu@tongwoo.cn
# @desc :
# @file : atcoder.py
# @software : PyCharm
import bisect
import copy
import sys
from sortedcontainers import SortedList
from collections import defaultdict, Counter, deque
from functools import lru_cache, cmp_to_key
import heapq
import math
sys.setrecursionlimit(100010)def main():items = sys.version.split()if items[0] == '3.10.6':fp = open("in.txt")else:fp = sys.stdinn = int(fp.readline())min_x, min_y, max_x, max_y = 10 ** 20, 10 ** 20, -10 ** 20, -10 ** 20uy, dy, lx, rx = [], [], [], []for i in range(n):items = fp.readline().strip().split()x, y = int(items[0]), int(items[1])d = items[2]if d == 'U':uy.append(y)min_x, max_x = min(min_x, x), max(max_x, x)elif d == 'D':dy.append(y)min_x, max_x = min(min_x, x), max(max_x, x)elif d == 'L':lx.append(x)min_y, max_y = min(min_y, y), max(max_y, y)else:rx.append(x)min_y, max_y = min(min_y, y), max(max_y, y)uy.sort()dy.sort()lx.sort()rx.sort()def get(t):x0, y0, x1, y1 = min_x, min_y, max_x, max_yif len(uy) > 0:y0 = min(uy[0] + t, y0)y1 = max(uy[-1] + t, y1)if len(dy) > 0:y0 = min(dy[0] - t, y0)y1 = max(dy[-1] - t, y1)if len(rx) > 0:x0 = min(rx[0] + t, x0)x1 = max(rx[-1] + t, x1)if len(lx) > 0:x0 = min(lx[0] - t, x0)x1 = max(lx[-1] - t, x1)return (y1 - y0) * (x1 - x0)lo, hi = 0, 10 ** 13c = 0ans = 1e18while c < 400:m0, m1 = lo + (hi - lo) / 3, hi - (hi - lo) / 3a0, a1 = get(m0), get(m1)if a0 > a1:lo = m0else:hi = m1ans = min(ans, a0)ans = min(ans, a1)c += 1print(ans)if __name__ == "__main__":main()相关文章:

AtCoder abc130
F题提交了无数遍,最后发现是三分求解的写法错了 C - Rectangle Cutting 盲猜都在xy的中心点时可以无限分割,否则不能 D - Enough Array 前缀和二分求位置 E - Common Subsequence 公共子序列求有几种组合 设 d p [ i ] [ j ] dp[i][j] dp[i][j]代表s取到…...
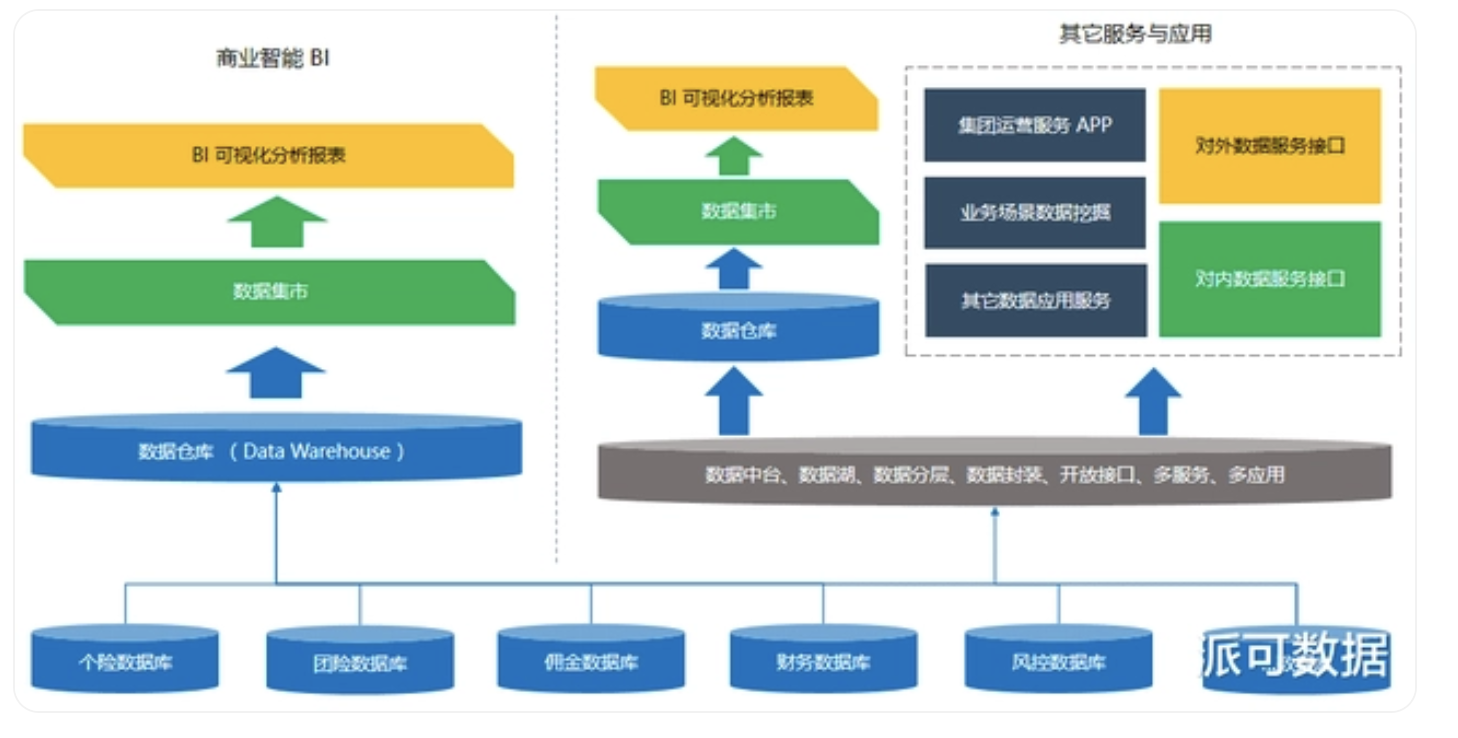
数据库、数据中台、数据仓库、数据湖区别
数据时代,各行业的企业都已经开始通过数据库来沉淀数据,但是真的论起数据库、数据仓库、数据中台,还是新出现的数据湖,它们的概念和区别,可能知道的人就比较少了,今天我们详细来比较了解一下。 一、数据仓…...

缺失的数据范围,思维,hduoj
Problem Description 著名出题人小Q出过非常多的题目,在这个漫长的过程中他发现,确定题目的数据范围是非常痛苦的一件事。 每当思考完一道题目的时间效率,小Q就需要结合时限以及评测机配置来设置合理的数据范围。 因为确定数据范围是一件痛苦…...
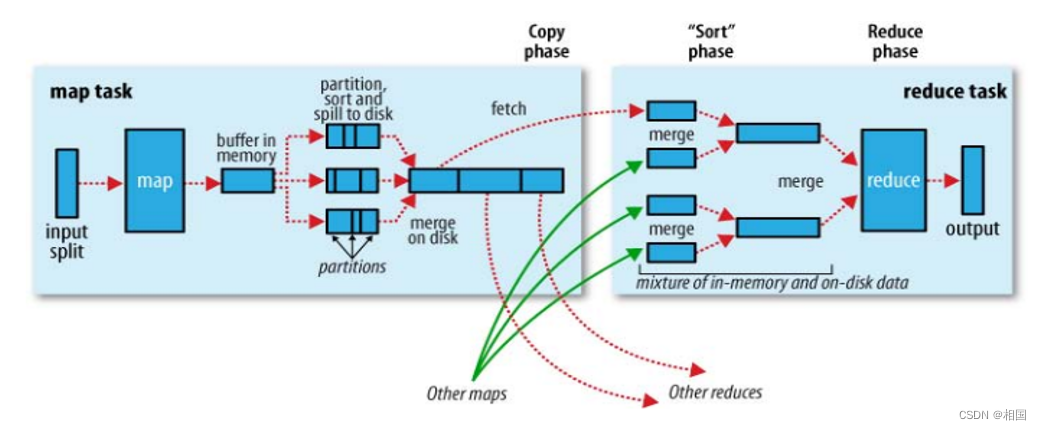
极简的MapReduce实现
目录 1. MapReduce概述 2. 极简MapReduce内存版 3. 复杂MapReduce磁盘版 4. MapReduce思想的总结 1. MapReduce概述 以前写过一篇 MapReduce思想 ,这次再深入一点,简单实现一把单机内存的。MapReduce就是把它理解成高阶函数,需要传入map和…...
)
更新暑假做过的项目(医学数据多标签分类与多标签分割,医学数据二分类)
写在前面 暑假参与了两个项目,收获颇多。搭建网络有许多走过的弯路与经验,调参也是一个必要的技能,在这里想一并分享给大家我在项目中积累的经验和一些小技巧。 PS:结合个人经验与网上经验,大家斟酌自取。 下面的几个…...

谷歌浏览器访问127.0.0.1时报错 Failed to read the ‘sessionStorage‘ property from ‘Window‘
谷歌浏览器访问 127.0.0.1 时报错如下: Uncaught DOMException: Failed to read the ‘sessionStorage’ property from ‘Window’: Access is denied for this document. 原因: 谷歌浏览器设置中禁止了 127.0.0.1 存储数据到浏览器设备上 解决方法…...
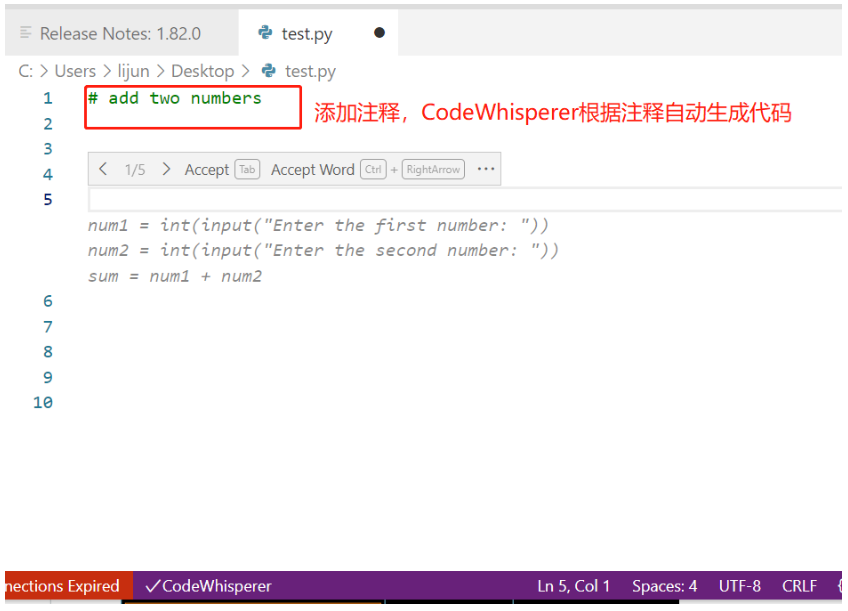
云技术分享 | 快速构建 CodeWhisperer 代码生成服务,让 AI 辅助编程
前言 Amazon CodeWhisperer 是 2023 年 4 月份发布的一款通用的、机器学习驱动的代码生成器服务,CodeWhisperer 经过数十亿行 Amazon 和公开可用代码的训练,可以理解用自然语言(英语)编写的评论,可在集成式开发环境 (…...

开发万岳互联网医院APP:技术要点和关键挑战
随着移动技术和互联网的飞速发展,互联网医院APP成为医疗领域的一项重要创新。这些应用程序为患者和医生提供了更多便利和互动性,但开发互联网医院APP也伴随着一系列的技术要点和关键挑战。本文将探讨互联网医院APP的技术要点以及在开发过程中需要面对的挑…...
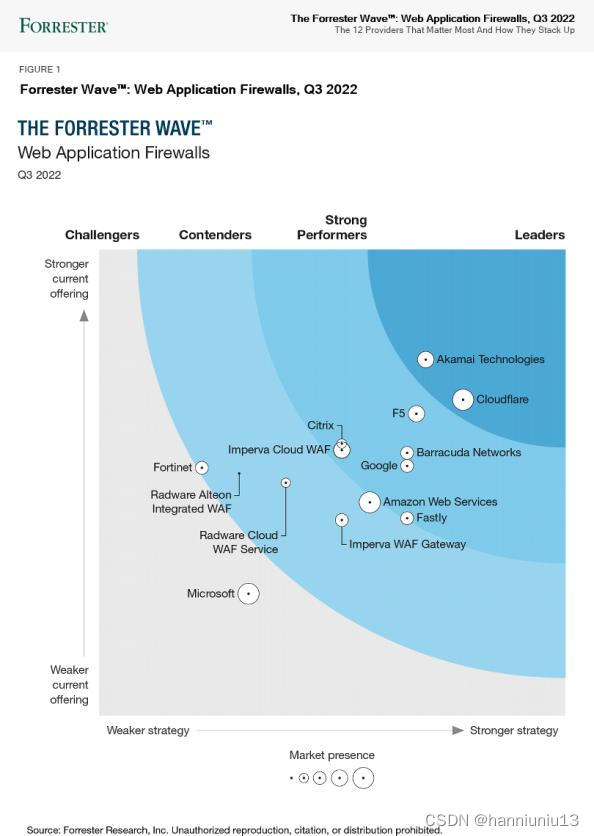
漫谈下一代防火墙与Web应用防火墙的区别
如今,Web应用程序变得越来越复杂,更是黑客非常感兴趣的目标。在谈到网络安全的话题时,我们总会讨论下一代防火墙与Web应用防火墙的区别。当已经拥有下一代防火墙(NGFW)时,为什么需要Web应用程序防火墙&…...

基于马尔可夫随机场的图像去噪算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1、马尔可夫随机场的基本原理 4.2、基于马尔可夫随机场的图像去噪算法 5.算法完整程序工程 1.算法运行效果图预览 原图: 加入噪声的图像: 滤波后的图像 迭代过程…...

【综合类型第 39 篇】HTTP 状态码详解
这是【综合类型第 39 篇】,如果觉得有用的话,欢迎关注专栏。 注: 本篇博客只是在「阿里云开发者社区版 HTTP 状态码详解」中按自己的写作风格做了断句,归纳整理,方便查看和阅读。 尊重原创,原文链接&…...

win10 hosts文件修改不生效
解决办法可以参考:修改hosts 不生效? 三种方法解决...
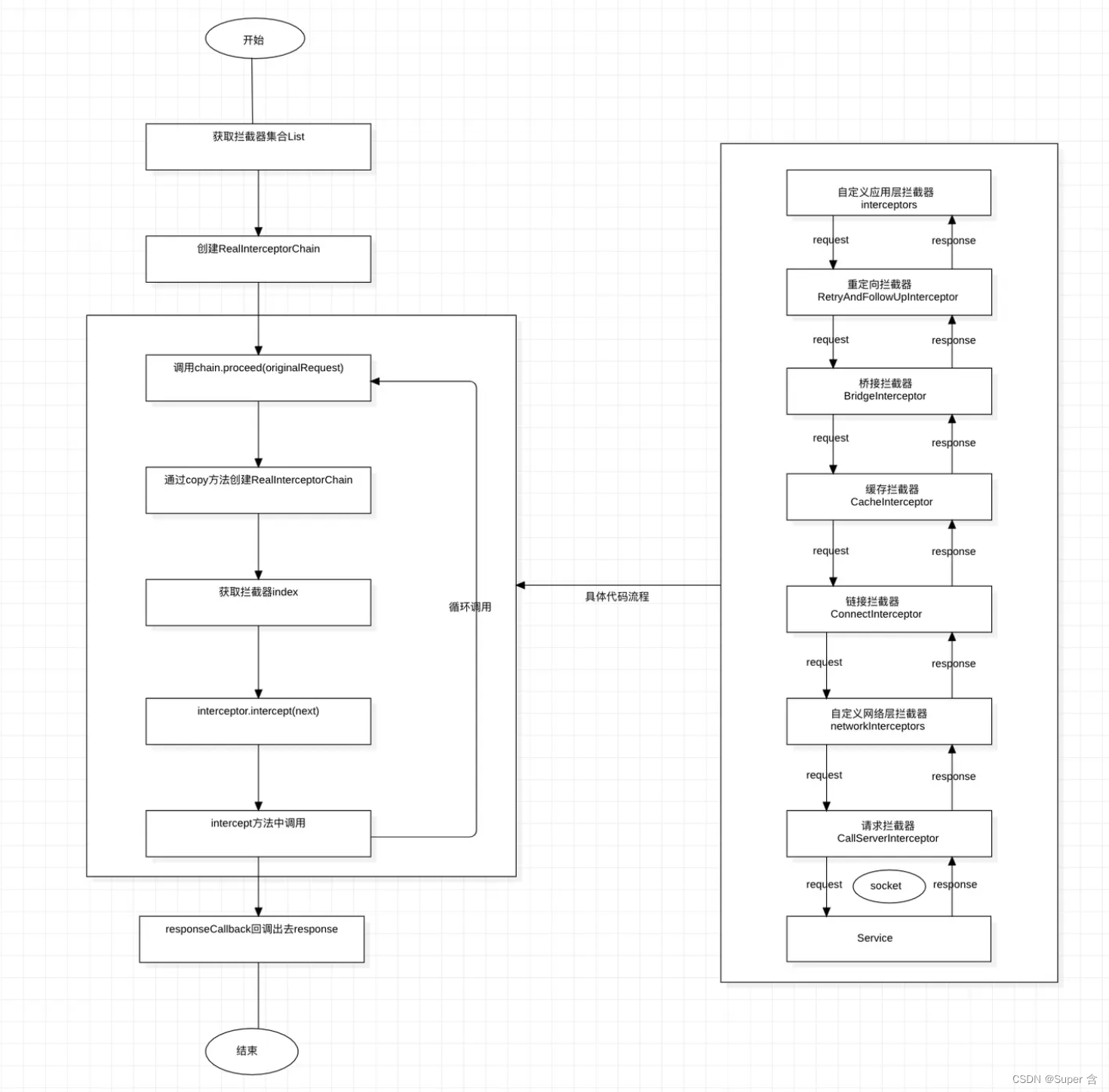
网络库OKHttp(1)流程+拦截器
序、慢慢来才是最快的方法。 背景 OkHttp 是一套处理 HTTP 网络请求的依赖库,由 Square 公司设计研发并开源,目前可以在 Java 和 Kotlin 中使用。对于 Android App 来说,OkHttp 现在几乎已经占据了所有的网络请求操作。 OKHttp源码官网 版…...
关于 Invalid bound statement (not found): 错误的解决
关于 Invalid bound statement not found: 错误的解决 前言错误原因解决方法1. 检查SQL映射文件2. 检查MyBatis配置3. 检查SQL语句4. 检查命名约定5. 清除缓存6. 启用日志记录 重点注意 结语 我是将军我一直都在,。! 前言 当开发Java Spring Boot应用程…...
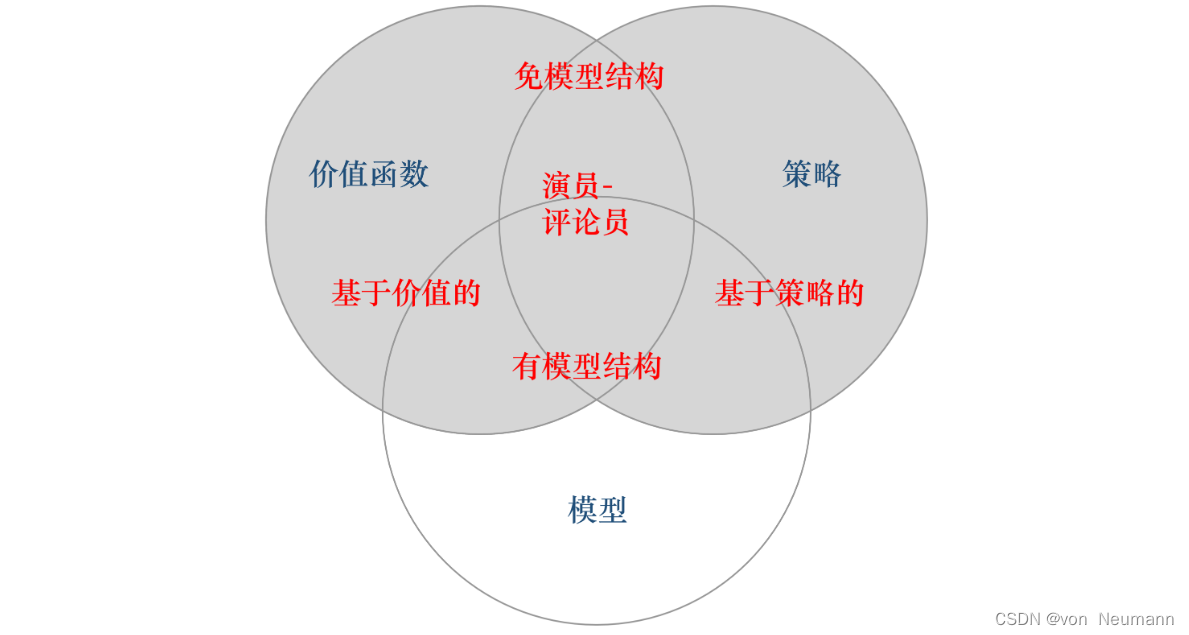
深入理解强化学习——智能体的类型:有模型强化学习智能体与免模型强化学习智能体
分类目录:《深入理解强化学习》总目录 根据智能体学习的事物不同,我们可以把智能体进行归类。基于价值的智能体(Value-based agent)显式地学习价值函数,隐式地学习它的策略。策略是其从学到的价值函数里面推算出来的。…...
vue项目获得开源代码之后跳过登录界面
readme运行 进入到账号和密码 找到main.js 比如说,以上这段代码 剩下next()就成功进入了...
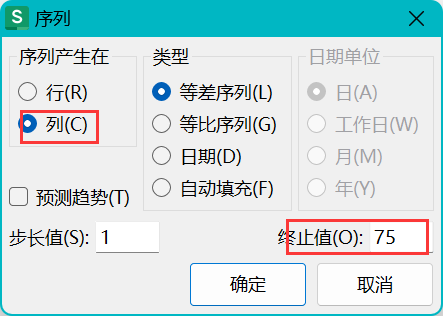
WPS、Excel表格增加一列,序列1到任意大小 / 填充某个范围的数字到列
Excel添加一列递增的数字方法有如下: 一、最常用的,使用鼠标放到右下角下拉增加 1、选中起始框的右下角,直到显示黑色实心十字 2、一直向下拖动 3、成功 这种填充方式是最常用的,100以内都可以轻松瞬间完成 1~100填充 但是如果…...
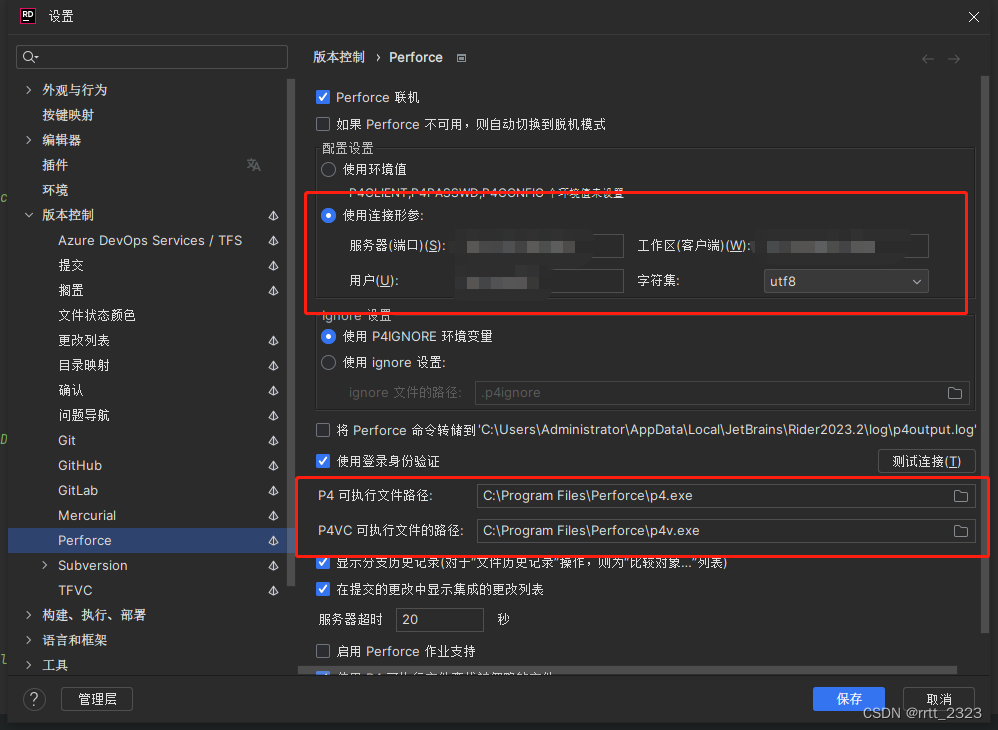
在 rider 里用配置 Perforce(P4)的注意事项
整个配置界面里,关键就配2处位置,但是都有些误导性。 1是连接形参的4个参数都得填,字符集看你项目的要求,这里工作区其实指的是你的工作空间,还不如显示英文的 Workspace 呢,搞得我一开始没填,…...
)
在Spring中,标签管理的Bean中,为什么使用@Autowired自动装配修饰引用类(前提条件该引用类也是标签管理的Bean)
Autowired是Spring框架的一个注解,它可以用来完成自动装配。 自动装配是Spring框架的一个特性,它可以避免手动去注入依赖,而是由框架自动注入。这样可以减少代码的重复性和提高开发效率。 在使用Autowired注解时,Spring会自动搜…...

俄罗斯YandexGPT 2在国家考试中获得高分;OpenAI API开发者快速入门指南
🦉 AI新闻 🚀 俄罗斯YandexGPT 2聊天机器人成功在国家考试中获得高分 摘要:俄罗斯YandexGPT 2聊天机器人通过国家统一考试文学科目,以55分的加权分数成功进入大学。Yandex团队强调他们在开发过程中确保数据库不包含任何关于统考…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
