分布式之PBFT算法
写在前面
在分布式之拜占庭问题 一文中我们分析了拜占庭问题,并一起看了支持拜占庭容错的口信消息性和签名消息性算法,但是这两种算法都有一个非常严重的问题,就是消息数量太多,通信的成本太大,消息数量复杂度为O(n ^ (f + 1)),其中f为判将数,所以导致这两种算法都不能在工程上实际落地,本文就一起来看下一个支持拜占庭容错的改进版本的算法PBFT,该算法的消息数量复杂度是O(n ^ 2),这个时间复杂度虽然也比较差,但要比O(n ^ (f + 1))好的多了,可以算得上是瘸子里的将军了。接下来我们就一起看下这位瘸子将军吧!
1:PBFT介绍
PBFT是一个支持拜占庭容错的分布式共识算法,其消息都是加密的不可篡改(这点类似秘钥消息型拜占庭问题之解),假定叛徒数为f,总节点数为n,则二者需要满足3f + 1<=n,因为该系统假定叛徒的人数为(n - 1)/3,若叛徒人数不满足要求,则该算法将不使用,如总结点数为4,则最多允许有4-1/3=1个叛徒,当然没有或更少的叛徒肯定是可以的。另外该算法通过3阶段提交来达成共识,如下:
预准备阶段
准备阶段
提交阶段
语言不是很好描述每个阶段,我们接下来通过一个实际的例子来看下。
2:实例
4节点1叛徒场景。
假定我们有客户端苏秦,leader赵,follower魏,follower韩,follower楚(叛徒),如下图:

假定苏秦某刻向楚发送进攻消息(即客户端向leader更新数据),如下图:

接着就进入到三阶段提交的第一阶段预准备阶段,分别向赵魏韩楚发出指令(同步客户端的更新),如下:
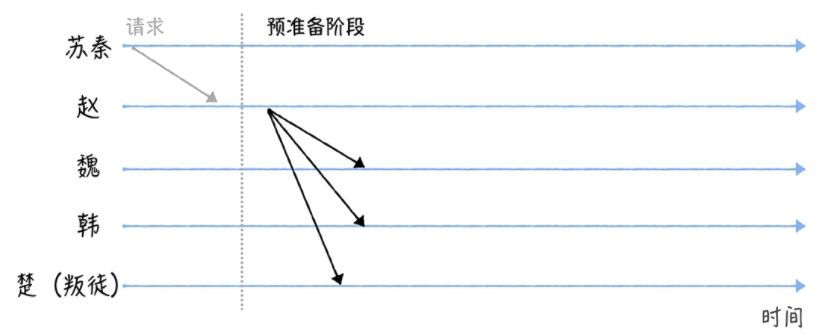
接着进入准备阶段,赵魏韩分别将受到的消息发送给对方,一旦某个节点收到了2f(这里因为f是1,所以就是2)个一致的消息时则进入到提交阶段,本例中叛徒楚因为其也不能伪造消息,所以就选择不发任何消息来扰乱达成共识的过程。如下图:
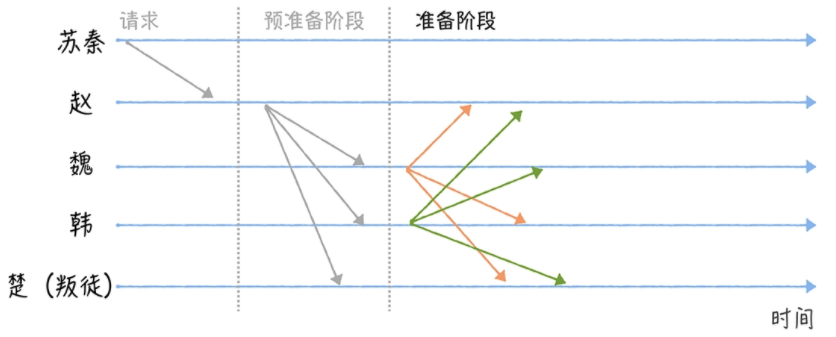
接下来进入提交阶段,告知其他节点自己已经准备到提交数据,当收到了2f+1(这里因为f是1,所以就是3)个消息时,则提交消息,如下图:
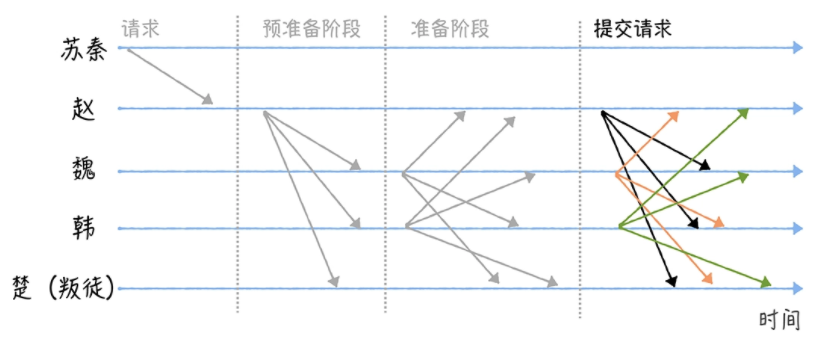
提交消息后返回成功给苏秦(leader),代表自己已经提交数据,当苏秦收到了f+1个提交的消息,则说明集群达成共识,如下图:
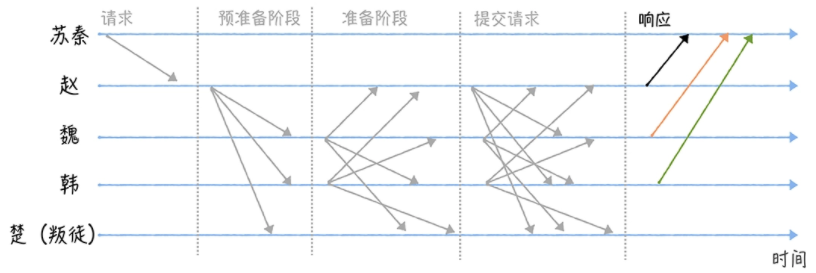
以上过程源码模拟参考这里 ,运行结果如下图:

3:交互次数分析
假定 13 节点集群中(f为4),则交互次数如下:
请求消息:1
预准备阶段:leader给所有的follower发消息,这里个数为13-1=12
准备阶段消息:只有可信节点才会发消息,可信节点数为8(不包括leader),因此发送消息数为8*12=96
提交阶段消息:除叛徒外的所有节点都要发送消息,因此总结点数是9(包括leader),因此发送消息数为9*12=108
回复消息:包括leader在内的所有非叛徒节点,都回复消息给客户端,因此消息数是9
因此总消息数就是226,可以看到消息交互次数还是蛮多的,但是支持拜占庭容错的要求本身就比较麻烦,所以该类算法都是比较耗时间的,有叛徒就是会比较麻烦。
写在后面
小结
本文分析了口信型拜占庭问题之解和签名消息型拜占庭问题之解因为消息通信量巨大而无法在工程上落地的问题,进而引入了本文分析的内容PBFT算法,并分析了其三阶段提交,预准备阶段,准备阶段,提交阶段,并给出了具体实例。希望本文能够帮助到你,也欢迎留言我们一起讨论。
参考文章列表
分布式之拜占庭问题 。
相关文章:

分布式之PBFT算法
写在前面 在分布式之拜占庭问题 一文中我们分析了拜占庭问题,并一起看了支持拜占庭容错的口信消息性和签名消息性算法,但是这两种算法都有一个非常严重的问题,就是消息数量太多,通信的成本太大,消息数量复杂度为O(n ^…...
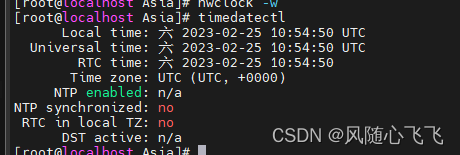
Linux 操作系统——查看/修改系统时区、时间、本地时间修改为UTC
文章目录1.背景描述2.知识储备3.解决步骤1. 查看当前时区2.修改设置Linux服务器时区3.复制相应的时区文件,替换系统时区文件;或者创建链接文件4. 查看和修改Linux的时间5. 硬件时间和系统时间的 相互同步1.背景描述 最近一个项目日期采用java8的LocalDa…...

CSS数据类型以及符号
css数据类型定义的是css属性中具有代表性的值,在规范的语法格式中,使用关键字外加一对 <和>表示,例如数值类型<number>、色值类型<color>等。 举个例子:background-image这个css属性语法结构如下: …...
LeetCode-54. 螺旋矩阵
题目来源 54. 螺旋矩阵 题目思路 while循环只遍历"环",不成环就不遍历了 四个边界 上边界 top : 0下边界 bottom : matrix.length - 1左边界 left : 0右边界 right : matrix[0].length - 1 矩阵不一定是方阵 top < bottom && left < r…...

【Python入门第十八天】Python For 循环
Python For 循环 for 循环用于迭代序列(即列表,元组,字典,集合或字符串)。 这与其他编程语言中的 for 关键字不太相似,而是更像其他面向对象编程语言中的迭代器方法。 通过使用 for 循环,我们…...

Qt图片定时滚动播放器
目录参考结构PicturePlay.promain.cpppictureplay.hpictureplay.cpppictureplay.ui效果源码参考 Qt图片浏览器 QT制作一个图片播放器 Qt中自适应的labelpixmap充满窗口后,无法缩小只能放大 可以显示jpg、jpeg、png、bmp。可以从电脑上拖动图到窗口并显示出来或者打开…...

李宏毅2023春季机器学习课程
目录2021&2022课程重磅须知我维护的其他项目更新日志课程地址课程资料直链课程作业直链其他优质课程2021&2022课程 CSDN Github 重磅须知 为方便所有网课资料与优质电子书籍的实时更新维护,创建一个在线实时网盘文件夹; 网盘获取方式&#…...

计算机操作系统知识点汇总
计算机操作系统选择填空题,300知识点,包含操作系统概论、处理机管理、内存管理、设备管理、文件管理等,为大学生期末创造奇迹提供无限可能 1、填空题 1、操作系统是对计算机资源进行管理的软件 2、操作系统是提供了处理机管理、 存储器管理…...

【离线数仓-8-数据仓库开发DWD层设计要点-交易域相关事实表】
离线数仓-8-数据仓库开发DWD层设计要点-交易域相关事实表离线数仓-8-数据仓库开发DWD层设计要点-交易域相关事实表一、DWD层设计要点二、交易域相关事实表1.交易域加购事务事实表1.加购事务事实表 前期梳理2.加购事务事实表 DDL表设计分析3.加购事务事实表 加载数据分析1.首日全…...
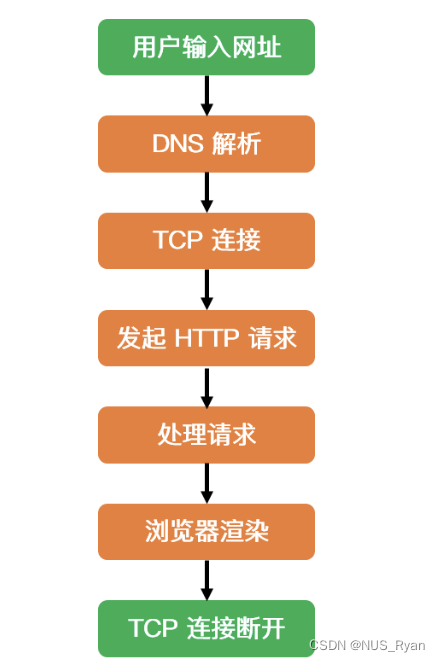
计算机网络(七):DNS协议和原理,DNS为什么用UDP,网页解析的全过程
文章目录一、什么是DNS二、DNS的作用三、DNS作用四、DNS为什么用UDP五、如果打开一个网站很慢,要如何排查六、网页解析的全过程一、什么是DNS DNS是域名系统的英文缩写,是一种组织成域层次结构的计算机和网络服务命名系统,用于TCP/IP网络。 …...
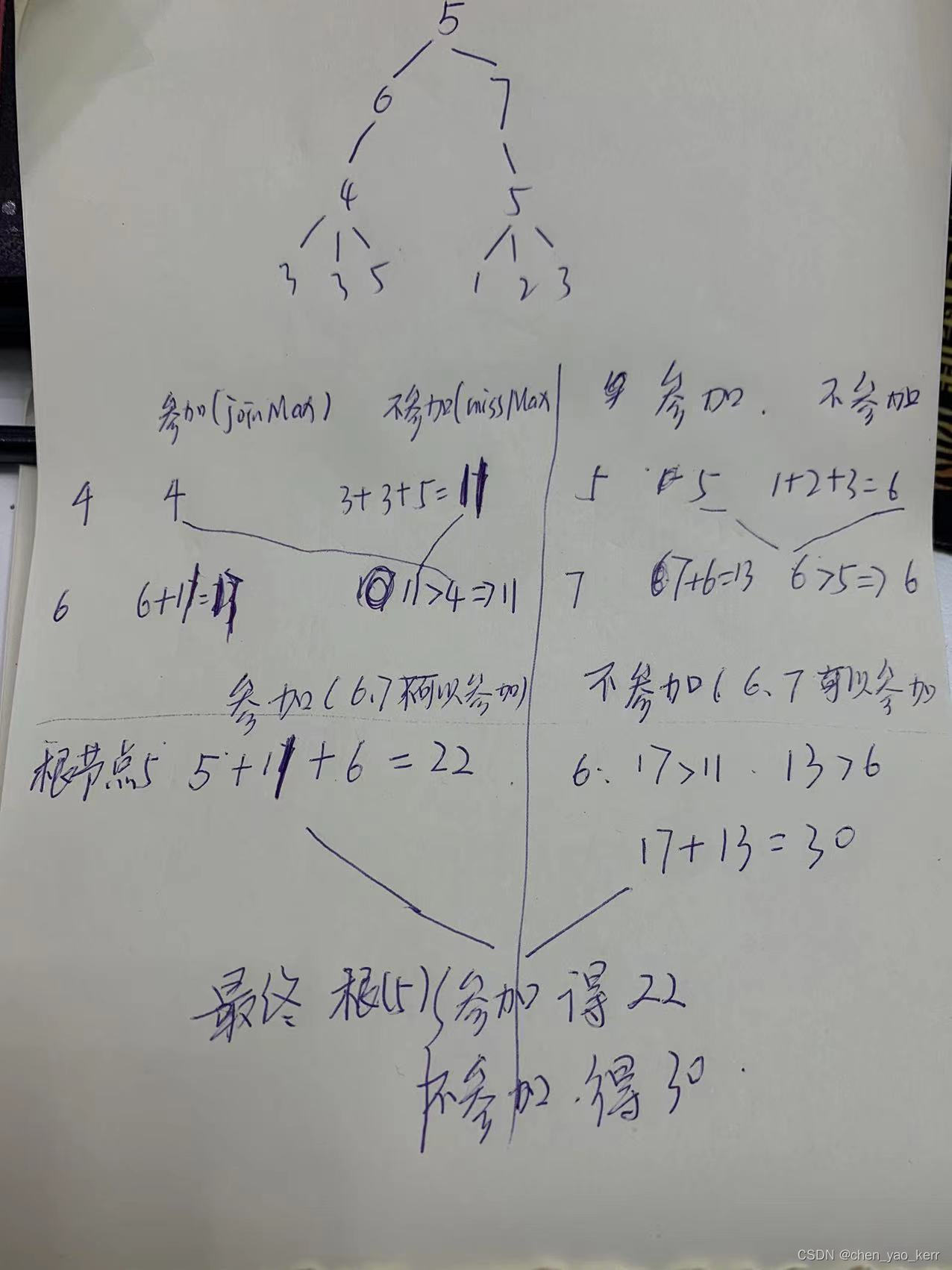
算法23:多叉树_派对的最大快乐值
公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。 叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外,每…...

中国ETC行业市场规模及未来发展趋势
中国ETC行业市场规模及未来发展趋势编辑根据市场调研在线网发布的2023-2029年中国ETC行业发展策略分析及战略咨询研究报告分析:随着政府坚持实施绿色出行政策,ETC行业也受到了极大的支持。根据中国智能交通协会统计,2017年中国ETC行业市场规模…...
——只出现一次的数字)
每日刷题(一)——只出现一次的数字
前言 今天遇到一个位运算的题目,感觉很有意思,记录一下。 Question1 136. 只出现一次的数字 给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实…...
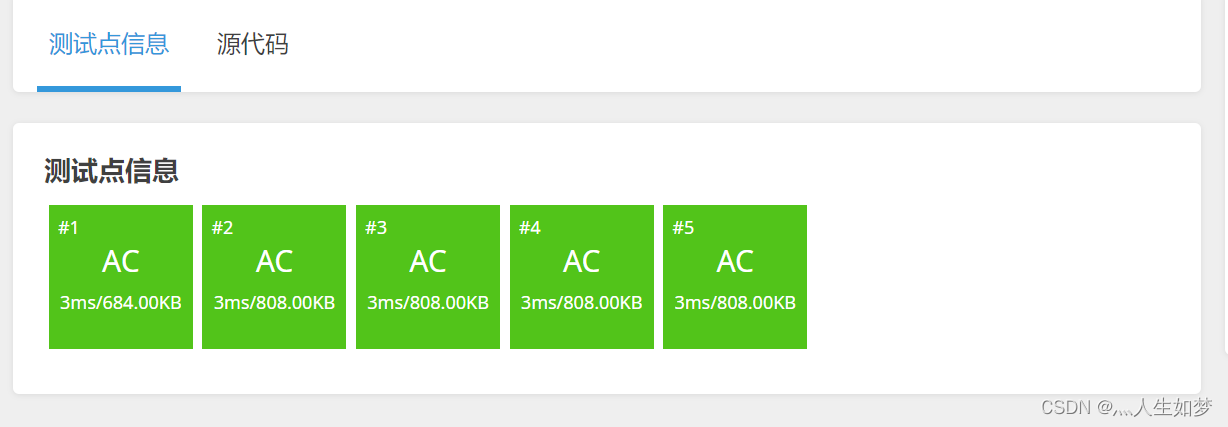
洛谷P5737 【深基7.例3】闰年展示 C语言/C++
【深基7.例3】闰年展示 题目描述 输入 x,yx,yx,y,输出 [x,y][x,y][x,y] 区间中闰年个数,并在下一行输出所有闰年年份数字,使用空格隔开。 输入格式 输入两个正整数 x,yx,yx,y,以空格隔开。 输出格式 第一行输出一个正整数&a…...

shell注释
注释对于任何编程语言都是不可忽视的重要组成部分,编写者通过注释来为其他人提供解释或提示,能有效提高代码的可读性。 Bash 同其他编程语言一样提供了两种类型注释的支持。 单行注释多行注释一、Bash 单行注释 在注释段落的开头使用 # ,如下…...
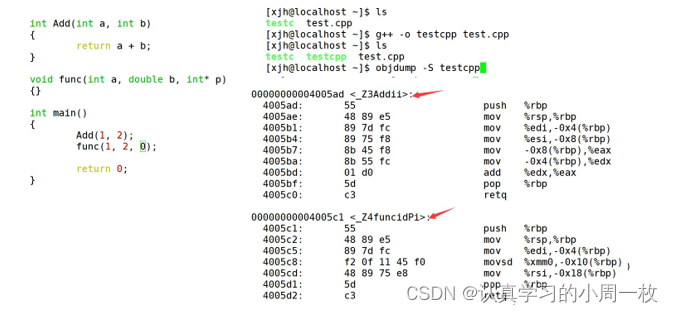
【C++入门(上篇)】C++入门学习
前言: 在之前的学习中,我们已经对初阶数据结构进行相应了学习,加上之前C语言的学习功底。今天,我们将会踏上更高一级“台阶”的学习-----即C的学习!!! 文章目录1.C 简介1.1什么是C1.2.C的发展史…...

【密码学】 一篇文章讲透数字签名
【密码学】 一篇文章讲透数字签名 数字签名介绍 数字签名(又称公钥数字签名)是只有信息的发送者才能产生的别人无法伪造的一段数字串,这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。它是一种类似写在纸上的普通的物理签名…...

POI导入导出、EasyExcel批量导入和分页导出
文件导入导出POI、EasyExcel POI:消耗内存非常大,在线上发生过堆内存溢出OOM;在导出大数据量的记录的时候也会造成堆溢出甚至宕机,如果导入导出数据量小的话还是考虑的,下面简单介绍POI怎么使用 POI导入 首先拿到文…...

手把手教你做微信公众号
手把手教你做微信公众号 微信公众号可以通过注册的方式来建立。 1.进入微信公众平台 首先,在浏览器中搜索微信公众号,网页第一个就是,如下图所示,我们点进去。 2.注册微信平台账号 进入官网之后,如下图所示&#…...
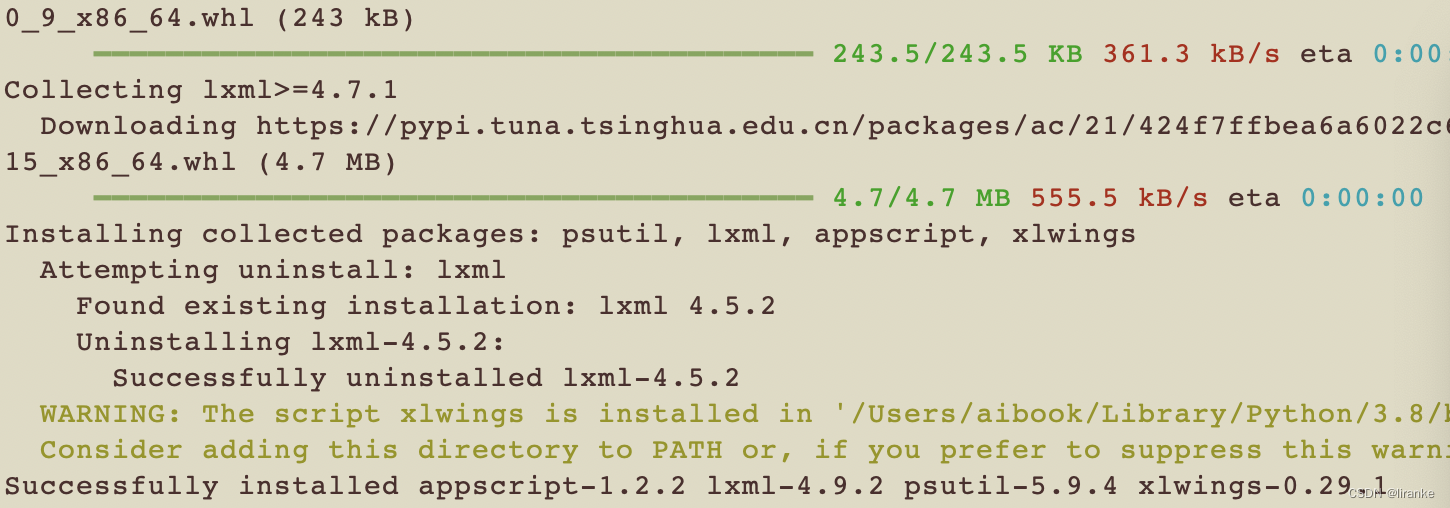
python-在macOS上安装python库 xlwings失败的解决方式
问题:python库 xlwings安装失败 今天,看到网上有wlwings库,可以用来处理excel表格,立刻想试一试。结果,安装这个python库失败了。经过排查,问题解决。 安装过程和错误提示: 我用最简单直接的…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
