二叉搜索树之AVL树
AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺
序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年 发明了一种
解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过
1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
平衡因子bf = 右子树高度 - 左子树高度
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在O(log_2 n),搜索时间
复杂度O(log_2 n)。
AVL树的插入
AVL树节点在定义时维护一个平衡因子,具体节点定义如下:
static class TreeNode{public int val;public int bf;//平衡因子public TreeNode left;public TreeNode right;public TreeNode parent;public TreeNode(int val){this.val = val;}}AVL树的插入过程可以分为两步:
1. 按照二叉搜索树的方式插入新节点
2. 调整节点的平衡因子
按照二叉搜索树的方式插入新节点:
public boolean insert(int val){TreeNode node = new TreeNode(val);if (root == null){root = node;return true;}TreeNode parent = null;TreeNode cur = root;while (cur != null){if (cur.val < val){parent = cur;cur = cur.right;}else if (cur.val == val){return false;}else {parent = cur;cur = cur.left;}}if (parent.val < val){parent.right = node;}else {parent.left = node;}node.parent = parent;cur = node;}调整节点的平衡因子
//平衡因子的修改while (parent != null){//先看cur是parent的左还是右 决定平衡因子是++还是--if (cur == parent.right){//如果是右树,那么右树高度增加 平衡因子++parent.bf++;}else {//如果是左树,那么左树高度增加 平衡因子--parent.bf--;}//检查当前的平衡因子 是不是绝对值 1 0 -1if (parent.bf == 0){//说明已经平衡了break;}else if (parent.bf == 1 || parent.bf == -1){//继续向上去修改平衡因子cur = parent;parent = cur.parent;}else {if (parent.bf == 2){//右树高-》需要降低右树的高度if (cur.bf == 1){//左单旋rotateLeft(parent);}else {//cur.bf == -1rotateRL(parent);}}else {//parent.bf == -2 左树高-》需要降低左树的高度if (cur.bf == -1){//右单旋rotateRight(parent);}else {//cur.bf == 1//左右双旋rotateLR(parent);}}//上述代码走完就已经平衡了break;}}左单旋-插入位置在较高右子树的右侧:(parent.bf = 2, cur.bf = 1)

//左单旋private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL= subR.left;parent.right = subRL;subR.left = parent;if (subRL != null){subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;if (parent == root){root = subR;root.parent = null;}else {if (pParent.left == parent){pParent.left = subR;}else {pParent.right = subR;}subR.parent = pParent;}subR.bf = 0;parent.bf = 0;}右单旋-插入位置在较高左子树的左侧:(parent.bf = -2, cur.bf = -1)
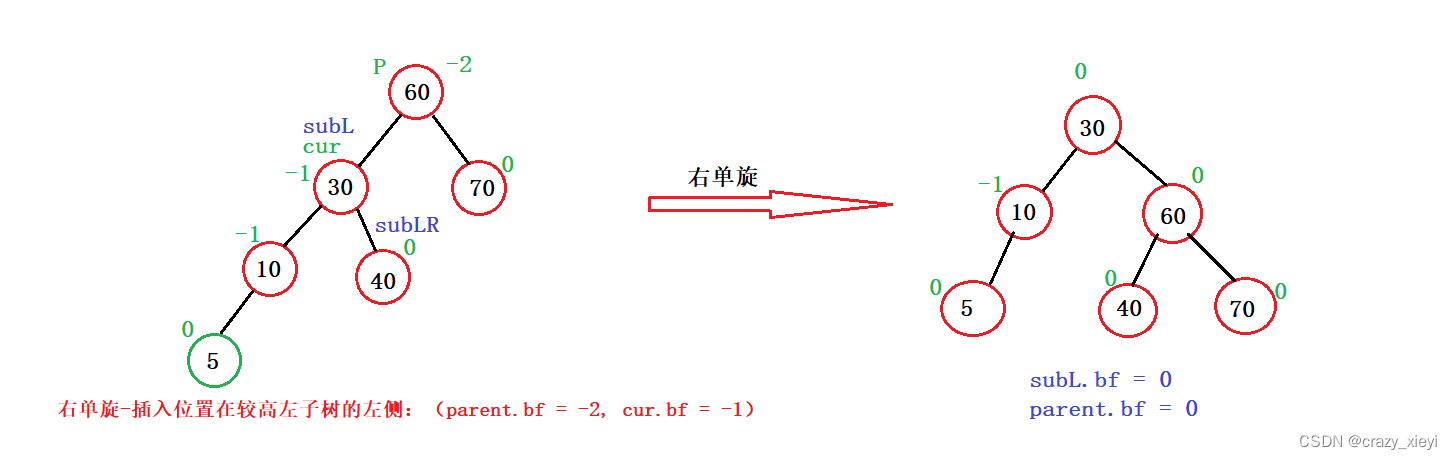
//右单旋private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;if (subLR != null){subLR.parent = parent;}//必须先记录当前的父亲的父亲节点TreeNode pParent = parent.parent;parent.parent = subL;//检查当前节点是不是根节点if (parent == root){root = subL;root.parent = null;}else {//不是根节点,判断这颗子树是左子树还是右子树if (pParent.left == parent){pParent.left = subL;}else {pParent.right = subL;}subL.parent = pParent;}subL.bf = 0;parent.bf = 0;}左右双旋-插入位置在较高左子树的右侧:(parent.bf = -2, cur.bf = 1)
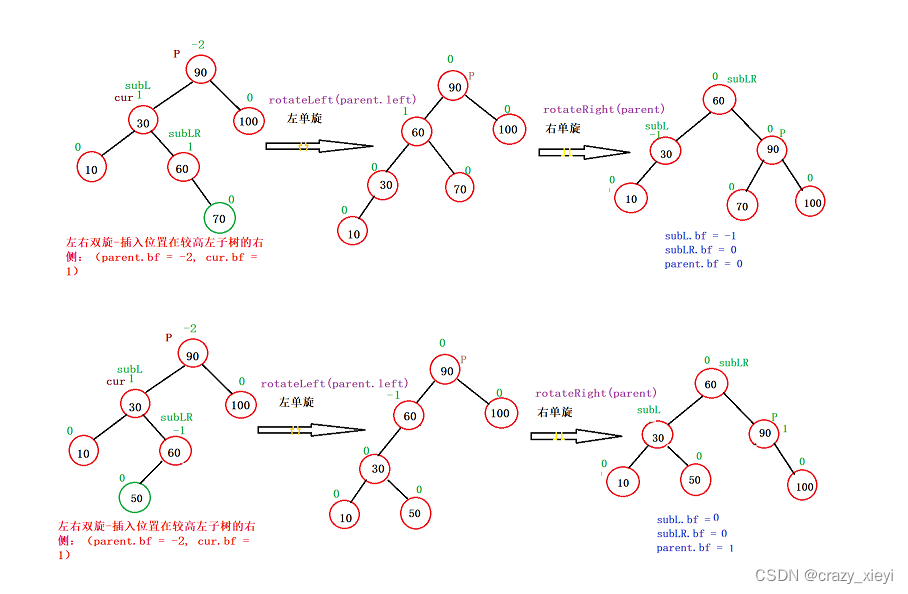
//左右双旋private void rotateLR(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR= subL.right;int bf = subLR.bf;rotateLeft(parent.left);rotateRight(parent);if (bf == -1){subL.bf = 0;subLR.bf = 0;parent.bf = 1;}else if (bf == 1){subL.bf = -1;subLR.bf = 0;parent.bf = 0;}}右左双旋-插入位置在较高右子树的左侧:(parent.bf = 2, cur.bf = -1)
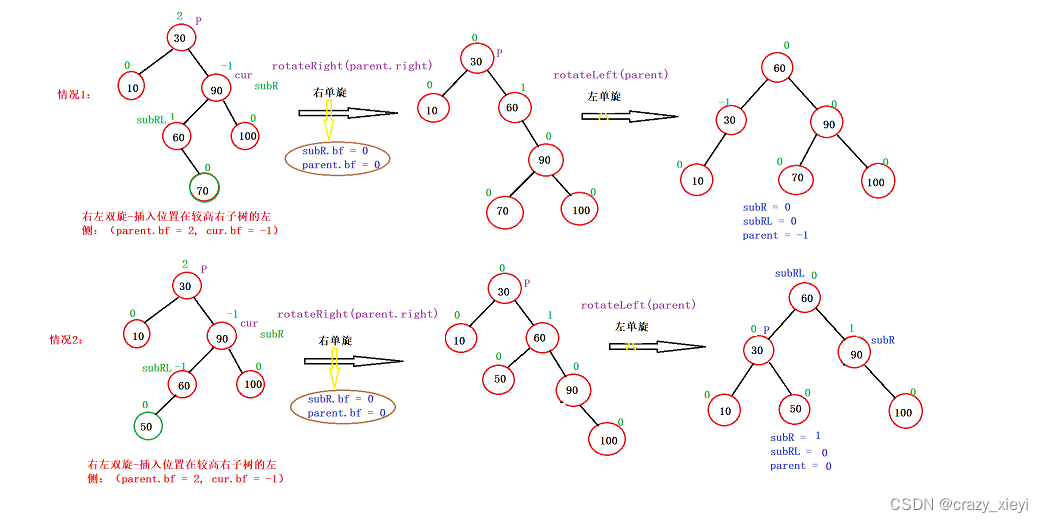
private void rotateRL(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;rotateRight(parent.right);rotateLeft(parent);if (bf == 1){subR.bf = 0;subRL.bf = 0;parent.bf = -1;}else if (bf == -1){subR.bf = 1;subRL.bf = 0;parent.bf = 0;}}AVL树插入操作的完整代码+验证代码
public class AVLTree {static class TreeNode{public int val;public int bf;//平衡因子public TreeNode left;public TreeNode right;public TreeNode parent;public TreeNode(int val){this.val = val;}}//根节点public TreeNode root;public boolean insert(int val){TreeNode node = new TreeNode(val);if (root == null){root = node;return true;}TreeNode parent = null;TreeNode cur = root;while (cur != null){if (cur.val < val){parent = cur;cur = cur.right;}else if (cur.val == val){return false;}else {parent = cur;cur = cur.left;}}if (parent.val < val){parent.right = node;}else {parent.left = node;}node.parent = parent;cur = node;//平衡因子的修改while (parent != null){//先看cur是parent的左还是右 决定平衡因子是++还是--if (cur == parent.right){//如果是右树,那么右树高度增加 平衡因子++parent.bf++;}else {//如果是左树,那么左树高度增加 平衡因子--parent.bf--;}//检查当前的平衡因子 是不是绝对值 1 0 -1if (parent.bf == 0){//说明已经平衡了break;}else if (parent.bf == 1 || parent.bf == -1){//继续向上去修改平衡因子cur = parent;parent = cur.parent;}else {if (parent.bf == 2){//右树高-》需要降低右树的高度if (cur.bf == 1){//左单旋rotateLeft(parent);}else {//cur.bf == -1rotateRL(parent);}}else {//parent.bf == -2 左树高-》需要降低左树的高度if (cur.bf == -1){//右单旋rotateRight(parent);}else {//cur.bf == 1//左右双旋rotateLR(parent);}}//上述代码走完就已经平衡了break;}}return true;}private void rotateRL(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;rotateRight(parent.right);rotateLeft(parent);if (bf == 1){subR.bf = 0;subRL.bf = 0;parent.bf = -1;}else if (bf == -1){subR.bf = 1;subRL.bf = 0;parent.bf = 0;}}//左右双旋private void rotateLR(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR= subL.right;int bf = subLR.bf;rotateLeft(parent.left);rotateRight(parent);if (bf == -1){subL.bf = 0;subLR.bf = 0;parent.bf = 1;}else if (bf == 1){subL.bf = -1;subLR.bf = 0;parent.bf = 0;}}//左单旋private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL= subR.left;parent.right = subRL;subR.left = parent;if (subRL != null){subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;if (parent == root){root = subR;root.parent = null;}else {if (pParent.left == parent){pParent.left = subR;}else {pParent.right = subR;}subR.parent = pParent;}subR.bf = 0;parent.bf = 0;}//右单旋private void rotateRight(TreeNode parent) {TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;if (subLR != null){subLR.parent = parent;}//必须先记录当前的父亲的父亲节点TreeNode pParent = parent.parent;parent.parent = subL;//检查当前节点是不是根节点if (parent == root){root = subL;root.parent = null;}else {//不是根节点,判断这颗子树是左子树还是右子树if (pParent.left == parent){pParent.left = subL;}else {pParent.right = subL;}subL.parent = pParent;}subL.bf = 0;parent.bf = 0;}//中序遍历public void inorder(TreeNode root){if (root == null)return;inorder(root.left);System.out.print(root.val + " ");inorder(root.right);}private int height(TreeNode root){if (root == null)return 0;int leftHeight = height(root.left);int rightHeight = height(root.right);return leftHeight > rightHeight ? leftHeight+1 : rightHeight+1;}public boolean isBalanced(TreeNode root){if (root == null)return true;int leftHeight = height(root.left);int rightHeight = height(root.right);if (rightHeight-leftHeight != root.bf){System.out.println("这个节点:"+root.val + "有异常!");return false;}return Math.abs(leftHeight-rightHeight) <= 1&& isBalanced(root.left)&& isBalanced(root.right);}
}AVL树的删除
因为AVL树也是二叉搜索树,可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,只不过与删除不
同的是,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。
1、找到需要删除的节点
2、按照搜索树的删除规则删除节点--参考https://blog.csdn.net/crazy_xieyi/article/details/127627063
3、更新平衡因子,如果出现了不平衡,进行旋转。--单旋,双旋
AVL树的性能分析
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询
时高效的时间复杂度,即 。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要
维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要
一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修
改,就不太适合。
相关文章:

二叉搜索树之AVL树
AVL树的概念二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年 发明了一种解决上…...
全栈自动化测试技术笔记(二):准备工作的切入点
自动化测试技术笔记(二):准备工作的切入点 上篇整理的技术笔记,聊了自动化测试的前期调研工作如何开展,最后一部分也提到了工作的优先级区分。 这篇文章,接上篇文章的内容,来聊聊自动化测试前期的准备工作࿰…...
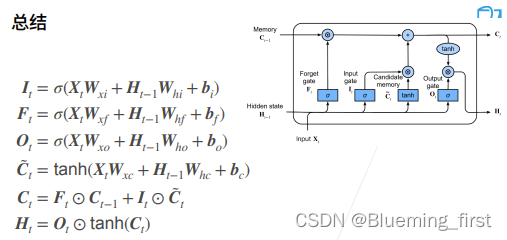
57 长短期记忆网络(LSTM)【动手学深度学习v2】
57 长短期记忆网络(LSTM)【动手学深度学习v2】 深度学习学习笔记 学习视频:https://www.bilibili.com/video/BV1JU4y1H7PC/?spm_id_fromautoNext&vd_source75dce036dc8244310435eaf03de4e330 长短期记忆网络(LSTM)…...
算法第十五期——动态规划(DP)之各种背包问题
目录 0、背包问题分类 1、 0/1背包简化版 【代码】 2、0/ 1背包的方案数 【思路】 【做法】 【代码】 空间优化1:交替滚动 空间优化2:自我滚动 3、完全背包 【思路】 【代码】 4、分组背包 核心代码 5、多重背包 多重背包解题思路1:转化…...
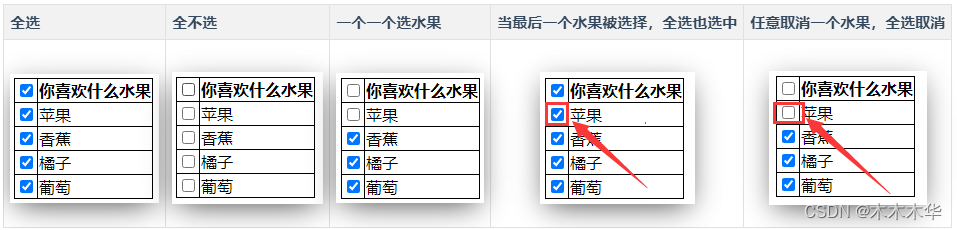
实现复选框全选和全不选的切换
今天,复看了一下JS的菜鸟教程,发现评论里面都是精华呀!! 看到函数这一节,发现就复选框的全选和全不选功能展开了讨论。我感觉挺有意思的,尝试实现了一下。 1. 全选、全不选,两个按钮ÿ…...
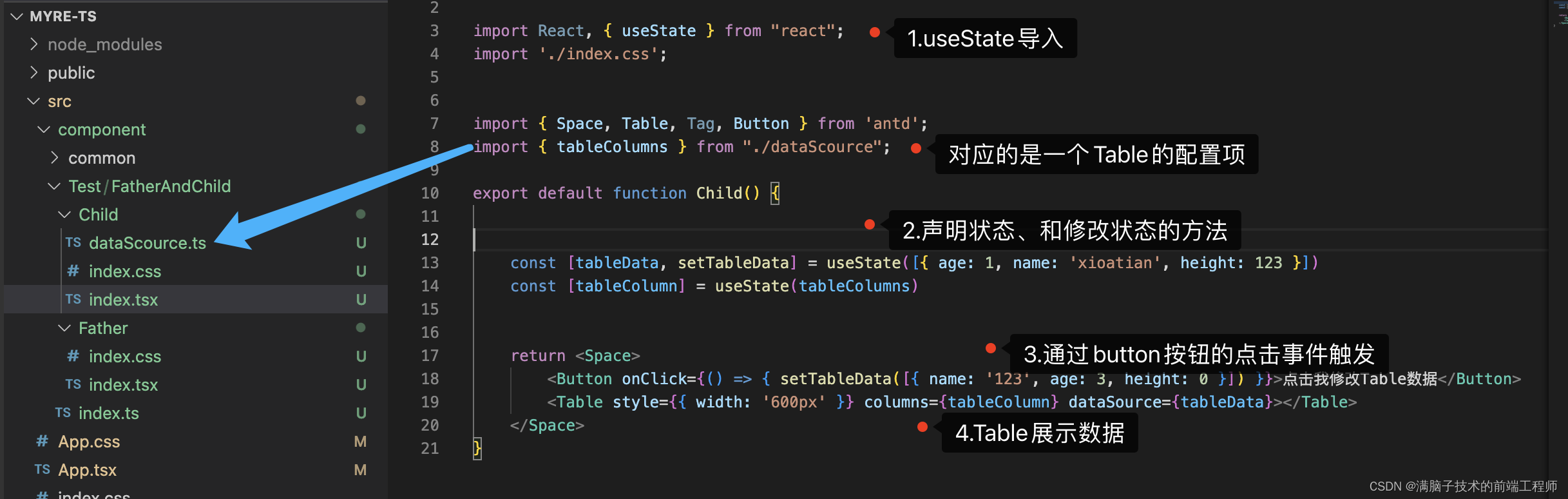
React hooks之useState用法(一)
系列文章目录 学习React已经有很长的一段时间了,今天决定重新回顾一下跟React相关的一些知识点 文章目录系列文章目录结构如下一、hooks是什么?useState可以能做什么二、如何使用useState()第一步:创建【函数组件&…...
spring的简单理解
目录 1 .ioc容器(控制反转) 2. Aop面向切面编程 3. 事务申明 4. 注解的方式启动 5. spring是什么与他的优势 6. 代理设计模式(比如aop) 7. springmvc中相应json数据 8. 使用lombok来进行对代码的简化 9. 使用logback记录…...
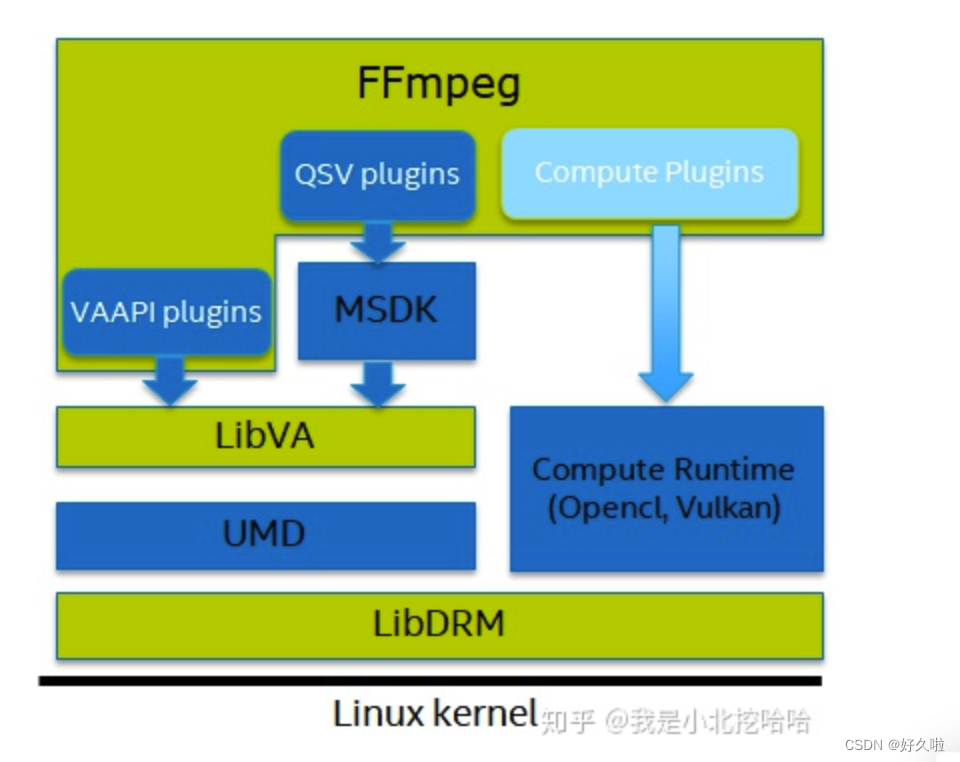
Docker调用Intel集显实现FFmpeg硬解码
文章目录Docker调用Intel集显实现FFmpeg硬解码参考FFmpeg 集成qsv方式一 容器完成所有步骤方式二 容器完成部分步骤方式三 dockerfile部署Docker调用Intel集显实现FFmpeg硬解码 参考 ffmpeg_qsv_docker拉取该镜像可以实现FFmpeg集成vaapi的硬加速,通过dockerfile文…...

端到端模型(end-to-end)与非端到端模型
一、端到端(end to end) 从输入端到输出端会得到一个预测结果,将预测结果和真实结果进行比较得到误差,将误差反向传播到网络的各个层之中,调整网络的权重和参数直到模型收敛或者达到预期的效果为止,中间所…...
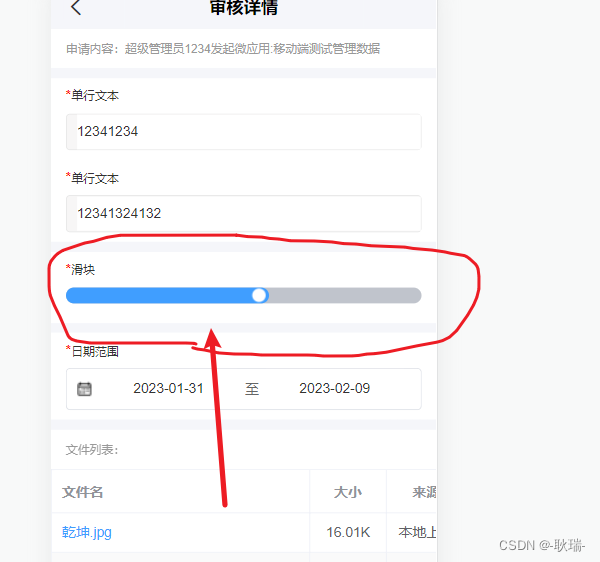
uniApp封装一个滑块组件
最近 项目中有一个需求 PC端动态设计的表单 移动端要能渲染出来 那么 就要去找到对应的组件 而其中 没有的 就包括滑块 没有又能怎么办 只能自己封装一个 我们直接上代码 <template><view class"u-slider" tap"onClick" :class"[disabled…...

运动基元(二):贝塞尔曲线
贝塞尔曲线是我第一个深入接触并使用于路径规划的运动基元。N阶贝塞尔曲线具有很多优良的特性,例如端点性、N阶可导性、对称性、曲率连续性、凸包性、几何不变性、仿射不变性以及变差缩减性。本章主要介绍贝塞尔曲线用于运动基元时几个特别有用的特性。 一、贝塞尔曲线的定义 …...

Android 11.0 关于Launcher3中调用截图功能总是返回null的解决方案
1.1概述 在11.0的系统产品开发中,在某些时候需要调用截图接口来进行截屏功能实现,而在Launcher3中发现调用系统截屏接口SurfaceControl.screenshot进行截图的时候始终为null, 获取不到系统当前页面的截屏功能,所以需要找到当前截屏失败的原因然后来实现截屏功能的实现,下面来…...

random随机数
random随机数 1.概述 random用来生成一些随机数,下面介绍random模块提供的方法根据需求生成不同的随机数。 2.random常用操作 2.1.random默认随机数 random()函数返回一个随机的浮点值,默认返回值范围在0 < n < 1.0区间 import randomfor i …...
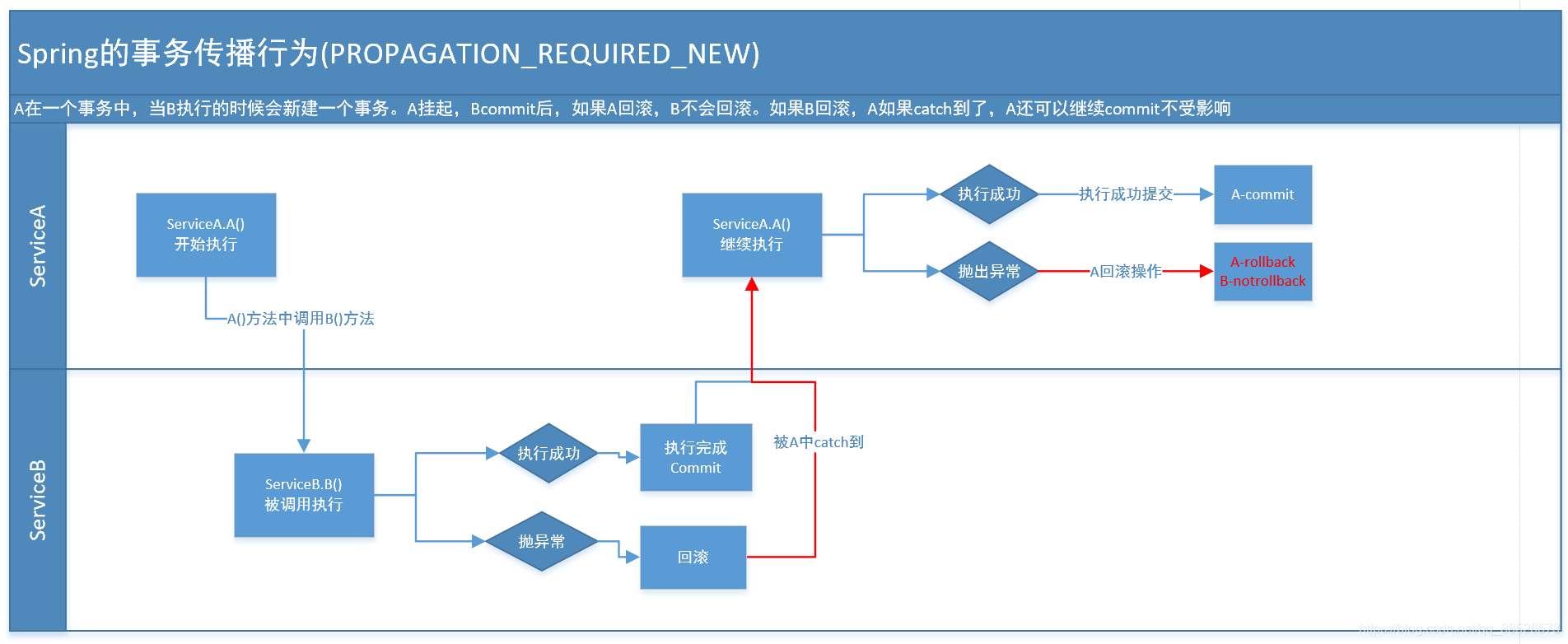
【金三银四系列】Spring面试题-上(2023版)
Spring面试专题 1.Spring应该很熟悉吧?来介绍下你的Spring的理解 有些同学可能会抢答,不熟悉!!! 好了,不开玩笑,面对这个问题我们应该怎么来回答呢?我们给大家梳理这个几个维度来回答 1.1 Spring的发展历程 先介绍…...

linux基本功系列之tar命令实战
文章目录前言一. tar命令介绍二. 语法格式及常用选项三. 参考案例3.1 仅打包不压缩3.2 打包后使用调用压缩命令进行压缩3.3 列出文件的内容3.4 追加文件到tar命令中3.5 释放文件到指定的目录四 . 各种压缩方式的比较总结前言 大家好,又见面了,我是沐风晓…...
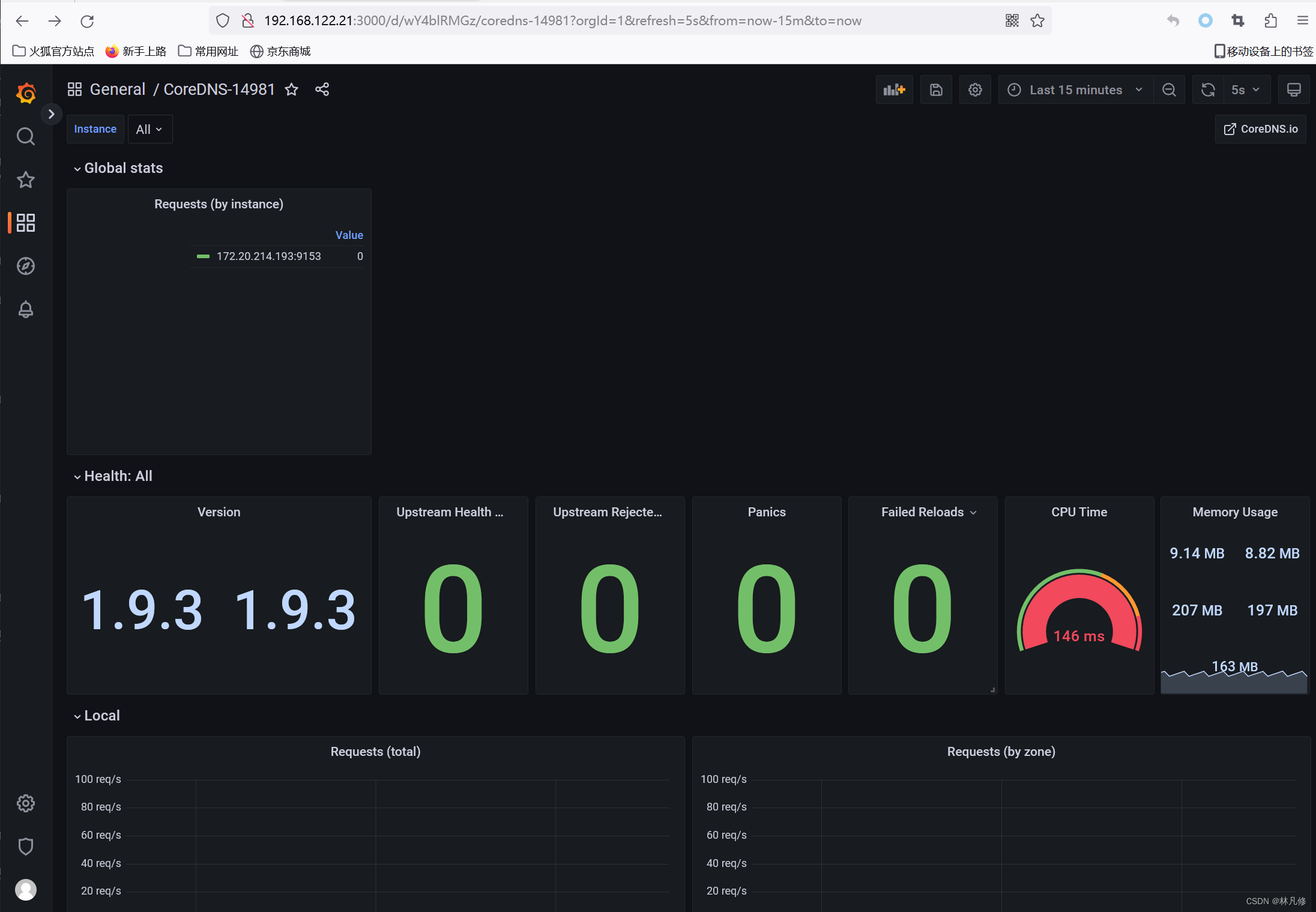
Prometheus服务发现
Prometheus服务发现介绍 Prometheus默认是采用pull的方式拉取监控数据的,每一个被抓取的目标都要暴露一个HTTP接口,prometheus通过这个接口来获取相应的指标数据,这种方式需要由prometheus-server决定采集的目标服务器有哪些,通过…...
【Spring6源码・MVC】请求处理流程源码解析
上一篇《【Spring6源码・MVC】初始化registry,完成url和controller的映射关系》我们知道,在IOC容器加载的同时,初始化了registry这个HashMap,这个HashMap中存放了请求路径和对应的方法。当我们请求进来,会通过这个regi…...

elasticsearch term match 查询
1. 准备数据 PUT h1/doc/1 {"name": "rose","gender": "female","age": 18,"tags": ["白", "漂亮", "高"] }PUT h1/doc/2 {"name": "lila","gender&quo…...
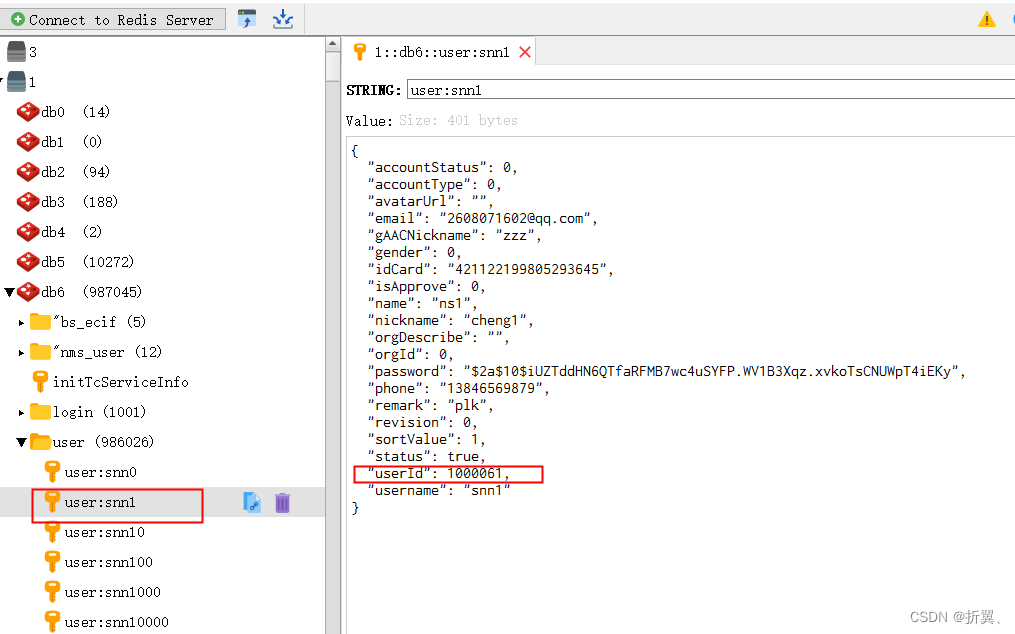
canal使用说明:MySQL、Redis实时数据同步
1. canal简介 canal是阿里开源的数据同步工具,基于bin log可以将数据库同步到其他各类数据库中,目标数据库支持mysql,postgresql,oracle,redis,MQ,ES等 canal分成服务端deployer和客户端adapter,我们可以部署多个,同时为了方便管…...

计算机视觉框架OpenMMLab开源学习(三):图像分类实战
前言:本篇主要偏向图像分类实战部分,使用MMclassification工具进行代码应用,最后对水果分类进行实战演示,本次环境和代码配置部分省略,具体内容建议参考前一篇文章:计算机视觉框架OpenMMLab开源学习&#x…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
