随机森林算法(Random Forest)R语言实现
随机森林
- 1. 使用Boston数据集进行随机森林模型构建
- 2. 数据集划分
- 3.构建自变量与因变量之间的公式
- 4. 模型训练
- 5. 寻找合适的ntree
- 6. 查看变量重要性并绘图展示
- 7. 偏依赖图:Partial Dependence Plot(PDP图)
- 8. 训练集预测结果
1. 使用Boston数据集进行随机森林模型构建
library(rio)
library(ggplot2)
library(magrittr)
library(randomForest)
library(tidyverse)
library(skimr)
library(DataExplorer)
library(caret)
library(varSelRF)
library(pdp)
library(iml)
data("boston")as.data.frame(boston)
skim(boston)#数据鸟瞰
plot_missing(boston)#数据缺失
#na.roughfix() #填补缺失
hist(boston$lstat,breaks = 50)
数据展示:
2. 数据集划分
######################################
# 1.数据集划分
set.seed(123)
trains <- createDataPartition(y = boston$lstat,p=0.70,list = F)
traindata <- boston[trains,]
testdata <- boston[-trains,]
3.构建自变量与因变量之间的公式
#因变量自变量构建公式
colnames(boston)
form_reg <- as.formula(paste0("lstat ~",paste(colnames(traindata)[1:15],collapse = "+")))
form_reg

构建的公式:

4. 模型训练
#### 2.1模型mtry的最优选取,mry=12 % Var explained最佳
#默认情况下数据集变量个数的二次方根(分类模型)或1/3(预测模型)
set.seed(123)
n <- ncol(boston)-5
errRate <- c(1) #设置模型误判率向量初始值
for (i in 1:n) {rf_train <- randomForest(form_reg, data = traindata,ntree = 1000,#决策树的棵树p =0.8,mtry = i,#每个节点可供选择的变量数目importance = T #输出变量的重要性)errRate[i] <- mean(rf_train$mse)print(rf_train)
}
m= which.min(errRate)
print(m)
结果:
Call:
randomForest(formula = form_reg, data = traindata, ntree = 1000, p = 0.8, mtry = i, importance = T)
Type of random forest: regression
Number of trees: 1000
No. of variables tried at each split: 1
Mean of squared residuals: 13.35016% Var explained: 72.5
Call:
randomForest(formula = form_reg, data = traindata, ntree = 1000, p = 0.8, mtry = i, importance = T)
Type of random forest: regression
Number of trees: 1000
No. of variables tried at each split: 2
Mean of squared residuals: 11.0119% Var explained: 77.31
Call:
randomForest(formula = form_reg, data = traindata, ntree = 1000, p = 0.8, mtry = i, importance = T)
Type of random forest: regression
Number of trees: 1000
No. of variables tried at each split: 3
Mean of squared residuals: 10.51724% Var explained: 78.33
Call:
randomForest(formula = form_reg, data = traindata, ntree = 1000, p = 0.8, mtry = i, importance = T)
Type of random forest: regression
Number of trees: 1000
No. of variables tried at each split: 4
Mean of squared residuals: 10.41254% Var explained: 78.55
Call:
randomForest(formula = form_reg, data = traindata, ntree = 1000, p = 0.8, mtry = i, importance = T)
Type of random forest: regression
Number of trees: 1000
No. of variables tried at each split: 5
Mean of squared residuals: 10.335% Var explained: 78.71
Call:
randomForest(formula = form_reg, data = traindata, ntree = 1000, p = 0.8, mtry = i, importance = T)
Type of random forest: regression
Number of trees: 1000
No. of variables tried at each split: 6
Mean of squared residuals: 10.22917% Var explained: 78.93
Call:
randomForest(formula = form_reg, data = traindata, ntree = 1000, p = 0.8, mtry = i, importance = T)
Type of random forest: regression
Number of trees: 1000
No. of variables tried at each split: 7
Mean of squared residuals: 10.25744% Var explained: 78.87
Call:
randomForest(formula = form_reg, data = traindata, ntree = 1000, p = 0.8, mtry = i, importance = T)
Type of random forest: regression
Number of trees: 1000
No. of variables tried at each split: 8
Mean of squared residuals: 10.11666% Var explained: 79.16
Call:
randomForest(formula = form_reg, data = traindata, ntree = 1000, p = 0.8, mtry = i, importance = T)
Type of random forest: regression
Number of trees: 1000
No. of variables tried at each split: 9
Mean of squared residuals: 10.09725% Var explained: 79.2
Call:
randomForest(formula = form_reg, data = traindata, ntree = 1000, p = 0.8, mtry = i, importance = T)
Type of random forest: regression
Number of trees: 1000
No. of variables tried at each split: 10
Mean of squared residuals: 10.09231% Var explained: 79.21
Call:
randomForest(formula = form_reg, data = traindata, ntree = 1000, p = 0.8, mtry = i, importance = T)
Type of random forest: regression
Number of trees: 1000
No. of variables tried at each split: 11
Mean of squared residuals: 10.12222% Var explained: 79.15

结果显示mtry为11误差最小,精度最高
5. 寻找合适的ntree
#### 寻找合适的ntree
set.seed(123)
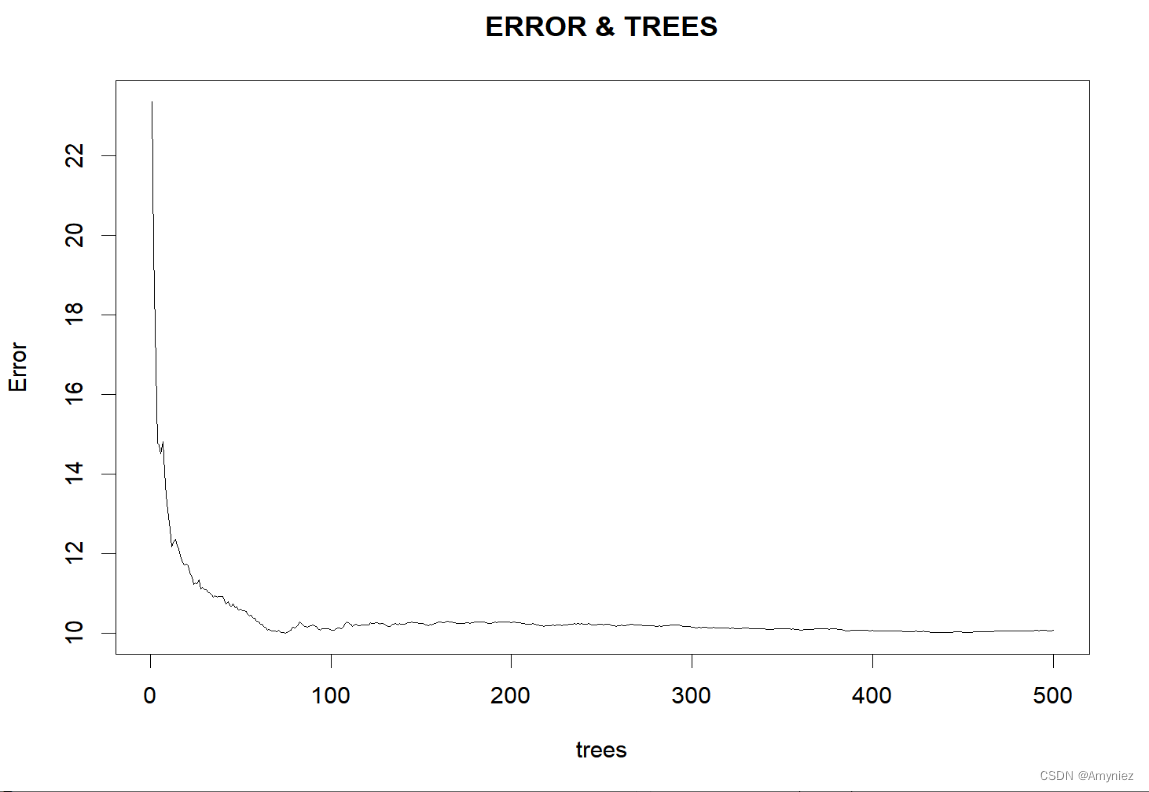
rf_train<-randomForest(form_reg,data=traindata,mtry=11,ntree=500,importance = T,proximity=TRUE)
plot(rf_train,main = "ERROR & TREES") #绘制模型误差与决策树数量关系图
运行结果:
6. 查看变量重要性并绘图展示
#### 变量重要性
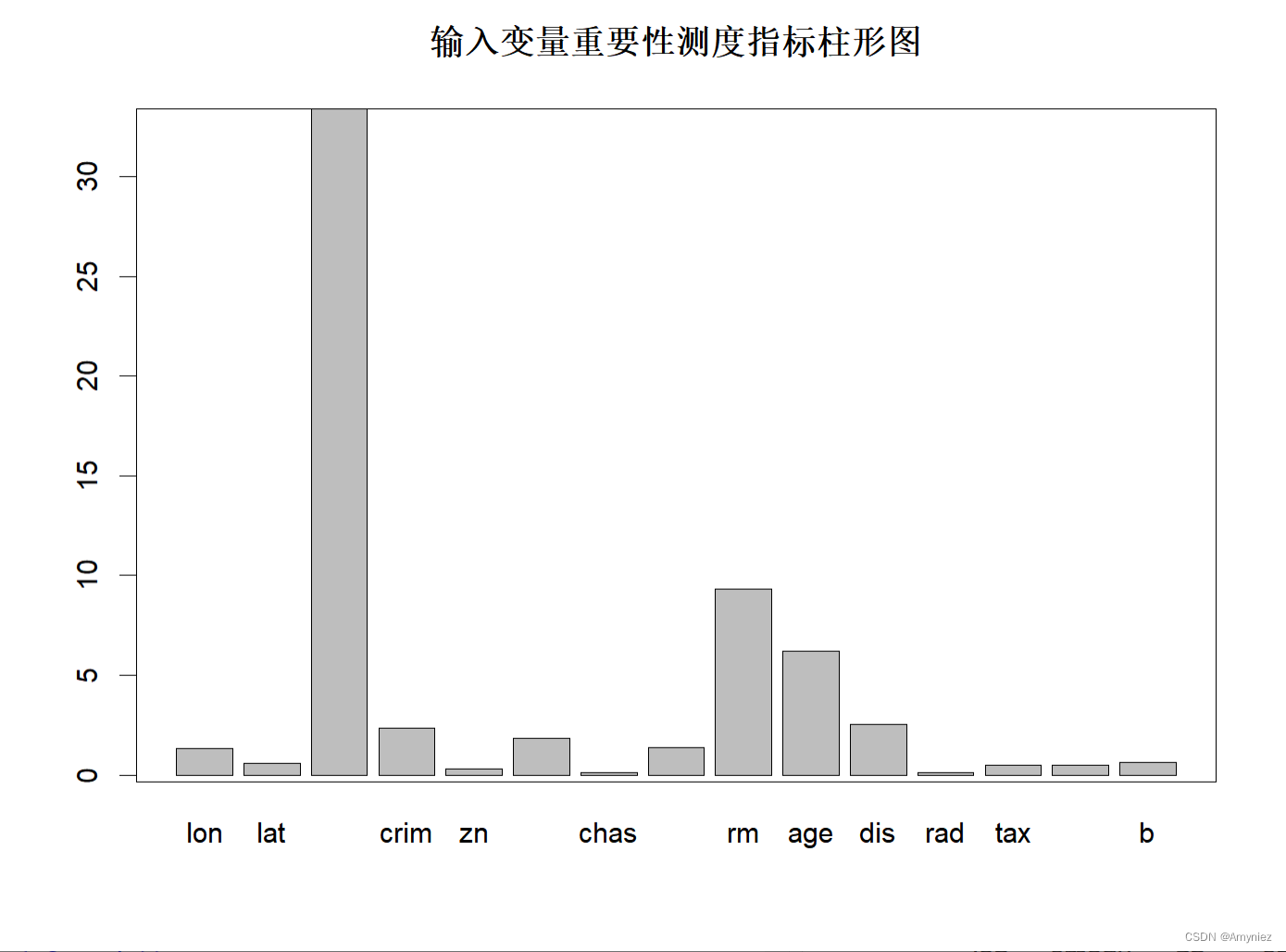
importance<-importance(rf_train) ##### 绘图法1
barplot(rf_train$importance[,1],main="输入变量重要性测度指标柱形图")
box()
重要性展示:
##### 绘图法2
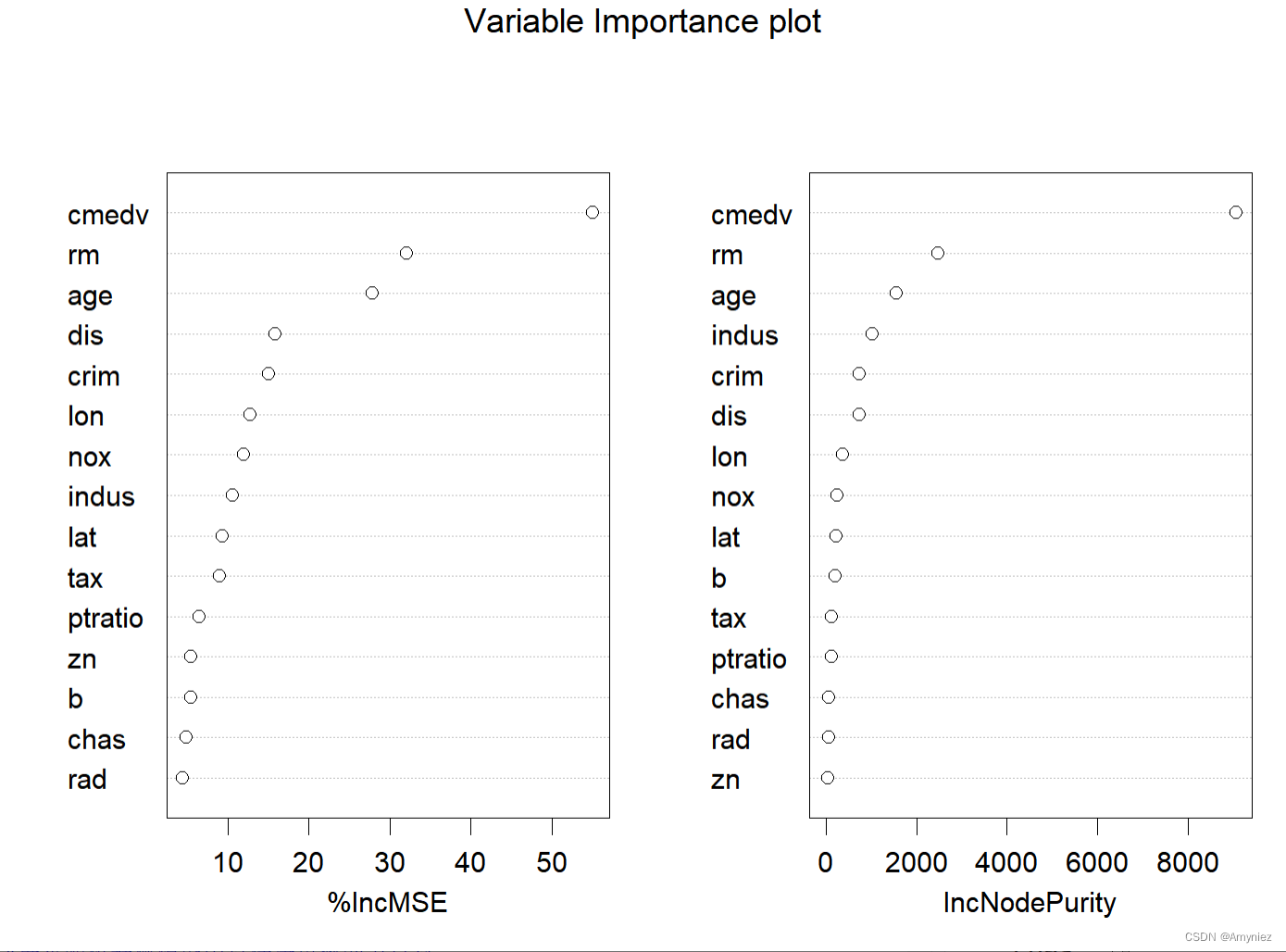
varImpPlot(rf_train,main = "Variable Importance plot")
varImpPlot(rf_train,main = "Variable Importance plot",type = 1)
varImpPlot(rf_train,sort=TRUE,n.var=nrow(rf_train$importance),main = "Variable Importance plot",type = 2) # 基尼系数
hist(treesize(rf_train)) #展示随机森林模型中每棵决策树的节点数
max(treesize(rf_train));
min(treesize(rf_train))
“%IncMSE” 即increase in mean squared error,通过对每一个预测变量随机赋值,如果该预测变量更为重要,那么其值被随机替换后模型预测的误差会增大。“IncNodePurity”即increase in node purity,通过残差平方和来度量,代表了每个变量对分类树每个节点上观测值的异质性的影响,从而比较变量的重要性。两个指示值均是判断预测变量重要性的指标,均是值越大表示该变量的重要性越大,但分别基于两者的重要性排名存在一定的差异。
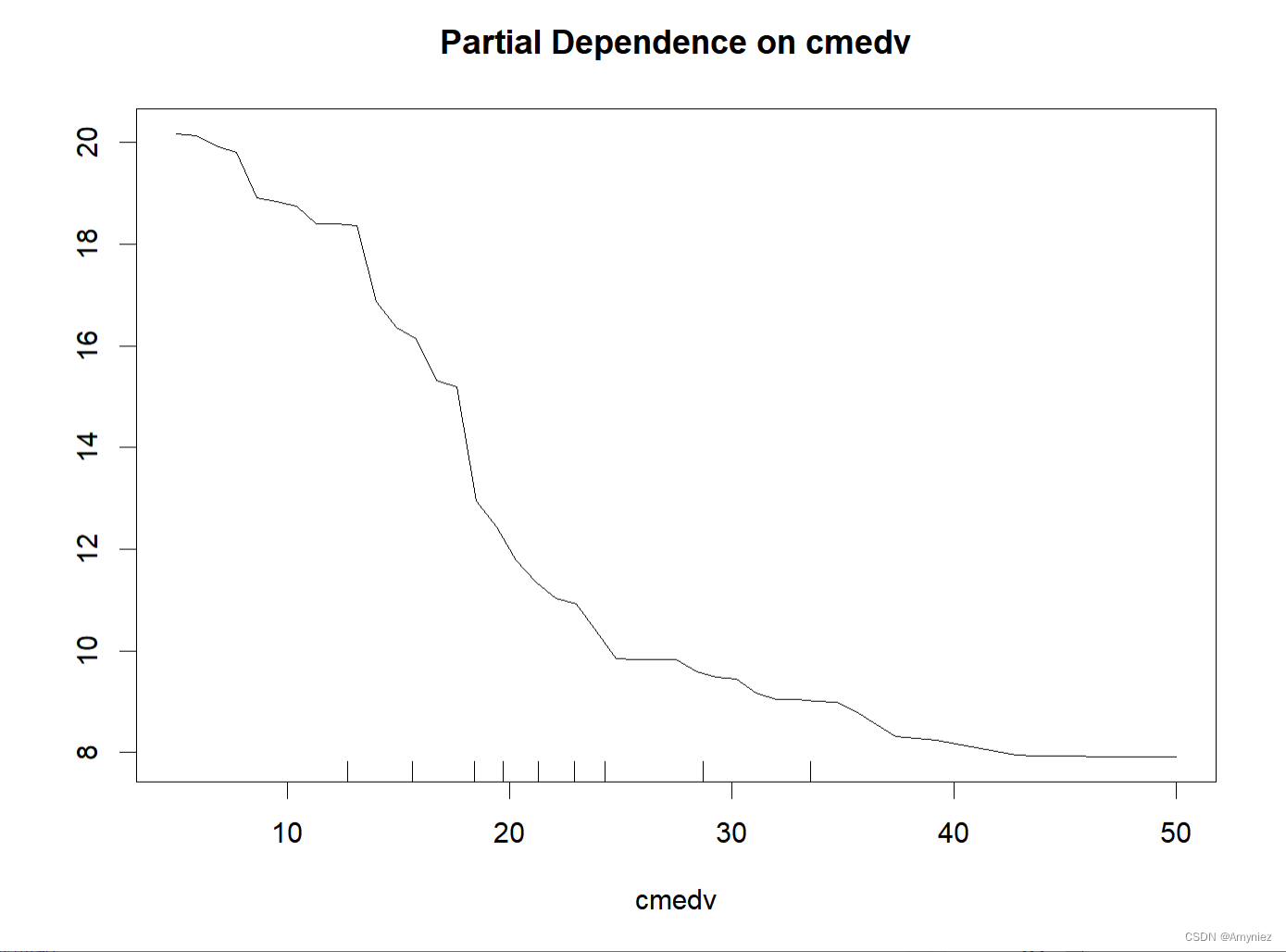
7. 偏依赖图:Partial Dependence Plot(PDP图)
部分依赖图可以显示目标和特征之间的关系是线性的、单调的还是更复杂的
缺点: 部分依赖函数中现实的最大特征数是两个,这不是PDP的错,而是2维表示(纸或屏幕)的错,是我们无法想象超过3维的错。
partialPlot(x = rf_train,pred.data = traindata,x.var = cmedv
)
PDP图:
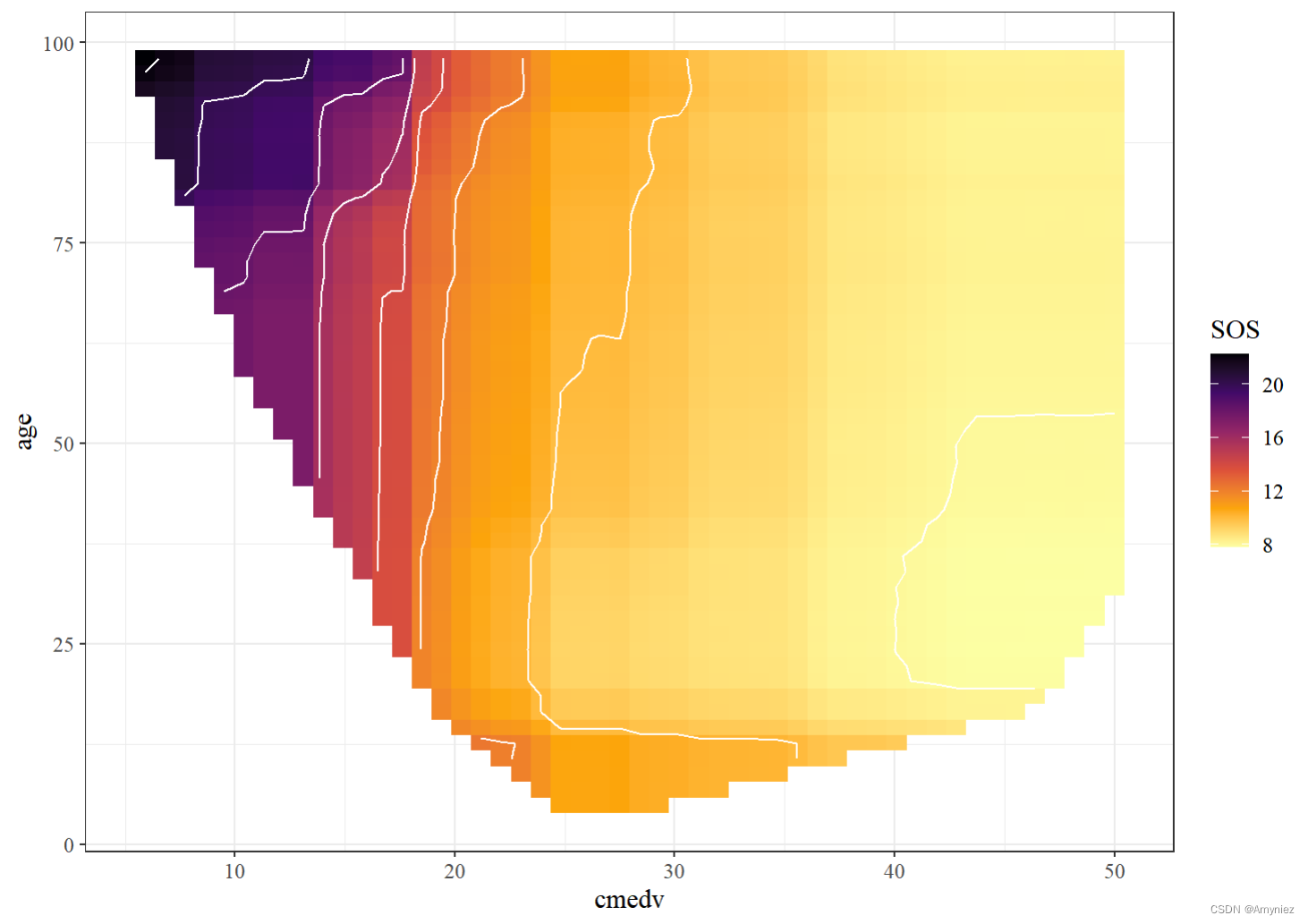
rf_train %>%partial(pred.var = c("cmedv", "age"), chull = TRUE, progress = TRUE) %>%autoplot(contour = TRUE, legend.title = "SOS",option = "B", direction = -1) + theme_bw()+theme(text=element_text(size=12, family="serif"))
交互结果展示:
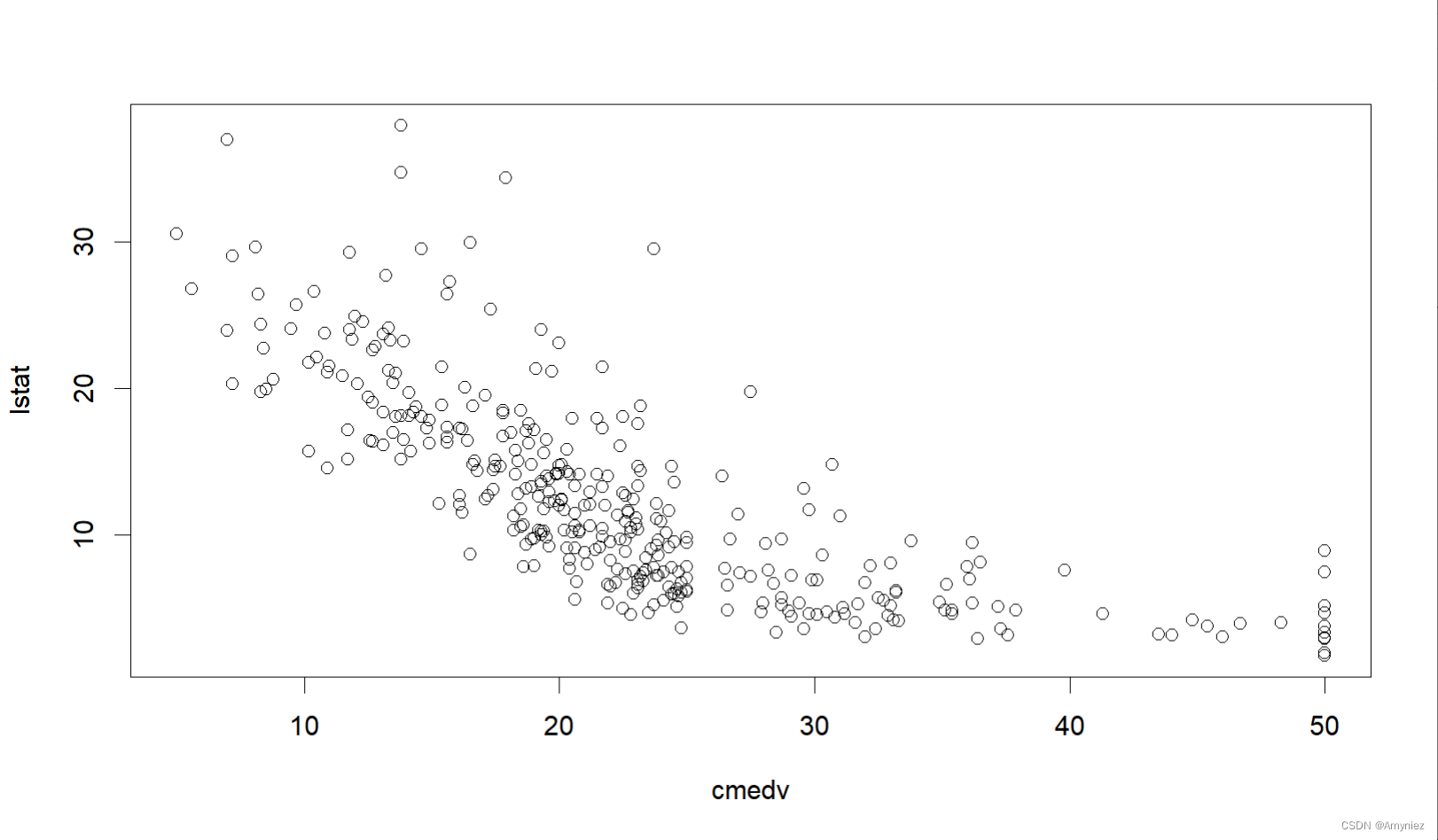
#预测与指标的关系散点图
plot(lstat ~ cmedv, data = traindata)
8. 训练集预测结果
#图示训练集预测结果
plot(x = traindata$lstat,y = trainpred,xlab = "实际值",ylab = "预测值",main = "随机森林-实际值与预测值比较"
)trainlinmod <- lm(trainpred ~ traindata$lstat) #拟合回归模型
abline(trainlinmod, col = "blue",lwd =2.5, lty = "solid")
abline(a = 0,b = 1, col = "red",lwd =2.5, lty = "dashed")
legend("topleft",legend = c("Mode1","Base"),col = c("blue","red"),lwd = 2.5,lty = c("solid","dashed"))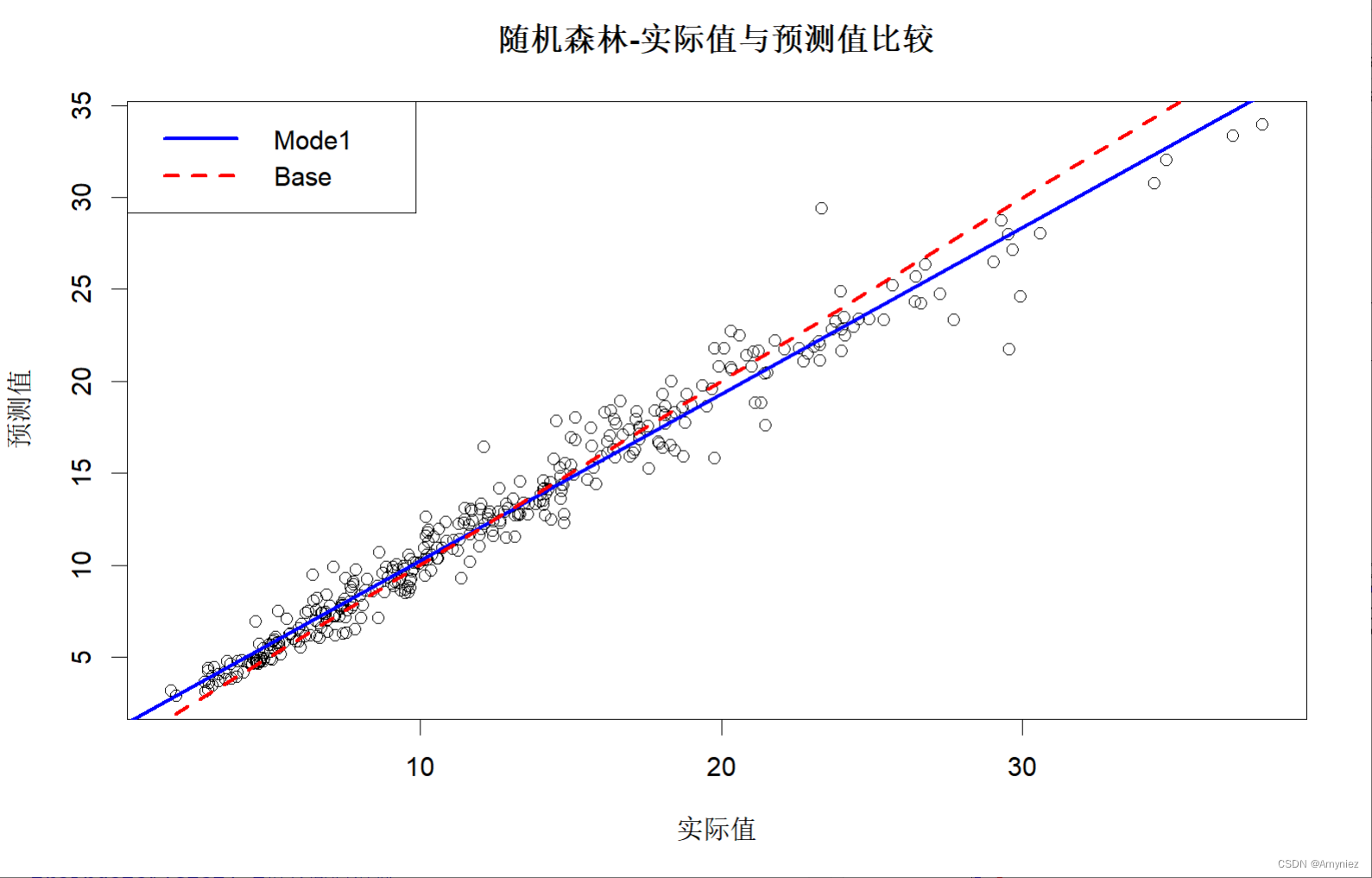
#测试集预测结果
testpred <- predict(rf_train,newdata = testdata)
#测试集预测误差结果
defaultSummary(data.frame(obs = testdata$lstat,pred = testpred))
#图示测试集结果
plot(x = testdata$lstat,y = testpred,xlab = "实际值",ylab = "预测值",main = "随机森林-实际值与预测值比较"
)
testlinmod <- lm(testpred ~ testdata$lstat)
abline(testlinmod, col = "blue",lwd =2.5, lty = "solid")
abline(a = 0,b = 1, col = "red",lwd =2.5, lty = "dashed")
legend("topleft",legend = c("Mode1","Base"),col = c("blue","red"),lwd = 2.5,lty = c("solid","dashed"))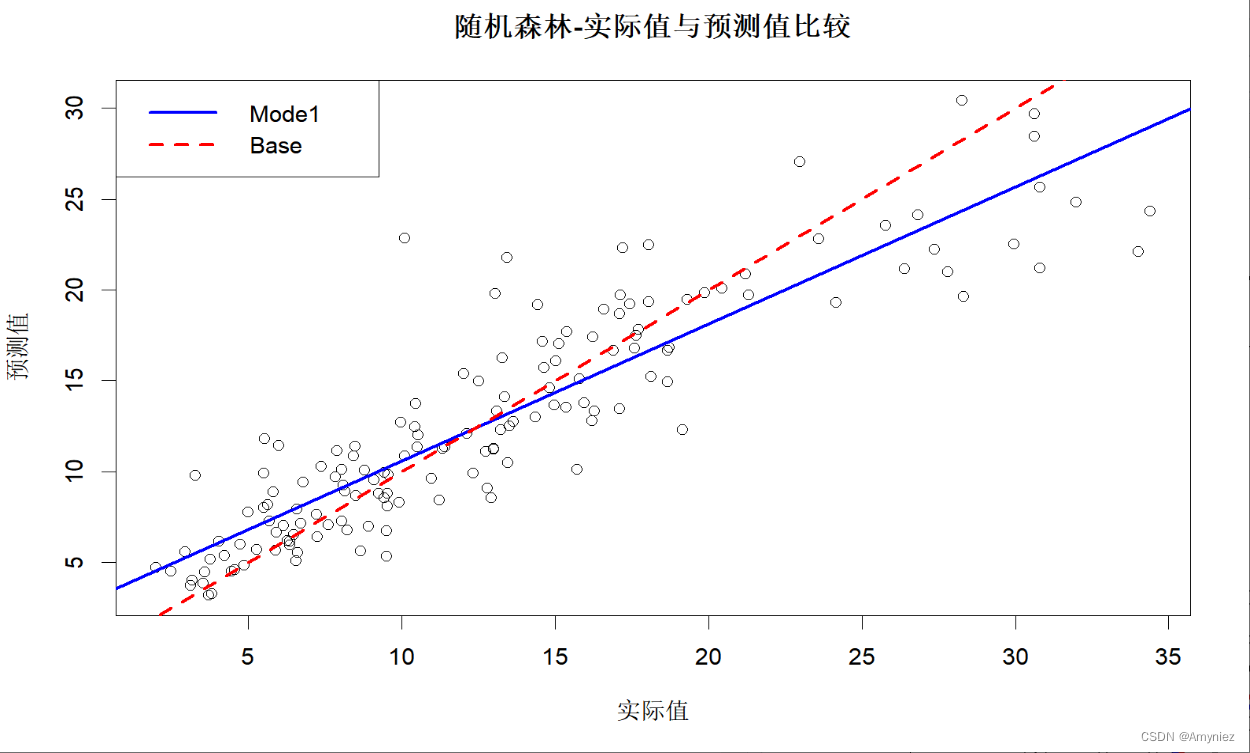
相关文章:

随机森林算法(Random Forest)R语言实现
随机森林1. 使用Boston数据集进行随机森林模型构建2. 数据集划分3.构建自变量与因变量之间的公式4. 模型训练5. 寻找合适的ntree6. 查看变量重要性并绘图展示7. 偏依赖图:Partial Dependence Plot(PDP图)8. 训练集预测结果1. 使用Boston数据集进行随机森…...
干货 | 八条“黄金规则”解决RF电路寄生信号
PART 01 接地通孔应位于接地参考层开关处流经所布线路的所有电流都有相等的回流。耦合策略固然很多,不过回流通常流经相邻的接地层或与信号线路并行布置的接地。在参考层继续时,所有耦合都仅限于传输线路,一切都非常正常。不过,如…...
Java虚拟机之类加载学习总结
文章目录1 什么是类加载1.1 类加载的应用1.2 类加载过程1.3 类的验证1.4 类初始化顺序2 类加载时机3 类加载器3.1 类加载分类3.2 双亲委派3.3 自定义类加载器3.4 类加载器的命名空间4 打破双亲委派4.1 线程上下文类加载器4.2 自定义类加载器5 类的卸载1 什么是类加载 Java 虚拟…...

基于 vue3、vite、antdv、css 变量实现在线主题色切换
1、前言动态切换主题是一个很常见的需求. 实现方案也有很多, 如:编译多套 css 文件, 然后切换类名(需要预设主题, 不够灵活)less 在线编译(不兼容 ie, 性能较差)css 变量(不兼容 ie)但是这些基本都是针对 vue2 的, 我在网上并没有找到比较完整的解决 vue3 换肤的方案, 大多只处…...

“笨办法”学Python 3 ——练习 44 继承和组合
练习44 继承和组合 永远记住这一点:继承的大多数用法都可以用组合(composition)来简化或替换。并且无论如何都要避免多重继承。 内容提要: 1. 什么是继承? (1)隐式继承 (2&#x…...

绕过安全狗拦截的SQL注入
目录 靶场环境及中间件 知识补充 判断存在注入 整形get类注入 字符型GET注入...

JAVA练习62-无重复字符的最长子串、最长回文子串
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、题目1-无重复字符的最长子串 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 二、题目2-最长回文子串 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 总…...

【JavaWeb】复习重点内容
✅✅作者主页:🔗孙不坚1208的博客 🔥🔥精选专栏:🔗JavaWeb从入门到精通(持续更新中) 📋📋 本文摘要:本篇文章主要分享JavaWeb的学习重点内容。 &a…...

基于粒子群改进的灰色神经网络的时间序列预测,PSO-GNN模型,神经网络案例之20
目标 灰色模型原理 神经网络原理 灰色神经网络原理 粒子群算法的原理 粒子群改进灰色神经网络原理 粒子群改进灰色神经网络的代码实现 效果图 结果分析 展望 灰色模型 基本思想是用原始数据组成原始序列(0),经累加生成法生成序列(1),它可以弱化原始数据的随机性,使其呈现…...
Java中的反射使用
1、获取Class对象的三种方式 1、对象调用Object类的getClass()方法(对象.getClass()) 2、调用类的class属性(类名.class) 3、调用Class类的静态方法(Class.forName(“包名.类名”))常用 Student类 package…...

urho3d工具
AssetImporter 加载开放资源导入库支持的各种三维格式(http://assimp.sourceforge.net/)并保存Urho3D模型、动画、材质和场景文件。有关支持的格式列表,请参阅http://assimp.sourceforge.net/main_features_formats.html. Blender的另一种导出路径是使用Urho3D插件…...
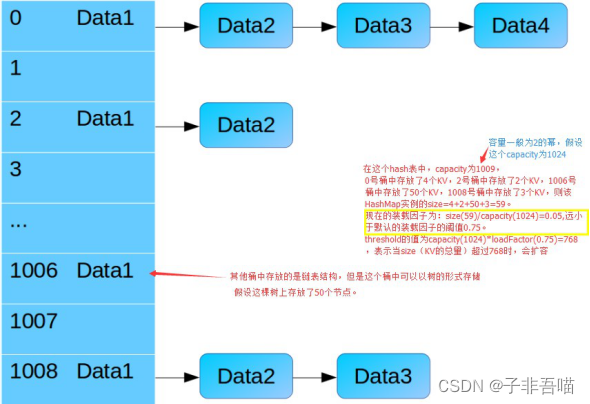
HashMap数据结构
HashMap概述 HashMap是基于哈希表的Map接口实现的,它存储的是内容是键值对<key,value>映射。此类不保证映 射的顺序,假定哈希函数将元素适当的分布在各桶之间,可为基本操作(get和put)提供稳定的性能。 HashMap在JDK1.8以前数据结构和存…...

BFC的含义以及应用
什么是BFC? BFC全称是Block Formatting context,翻译过来就是块级格式化上下文。简单来说,BFC是一个完全独立的空间。让空间里的子元素不会影响到外面的布局。😃😃😃 如何触发BFC呢? mdn给了如下方式&a…...

电脑技巧:分享8个Win11系统必备小技巧
目录 1、让任务栏显示“右键菜单” 2、任务栏置顶 3、还原经典右键菜单 4、Win11版任务管理器 5、新版AltTab 6、开始菜单不再卡 7、为Edge浏览器添加云母效果 8、自动切换日/夜模式 Win11在很多地方都做了调整,但由于涉及到诸多旧有习惯,再加上…...
C/C++每日一练(20230226)
目录 17. 电话号码的字母组合 37. 解数独 51. N 皇后 52. N皇后 II 89. 格雷编码 90. 子集 II 17. 电话号码的字母组合 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电…...

Vue 3第二章:Vite文件目录结构及SFC语法
文章目录1. Vite 文件目录结构2. Vue3 SFC 语法规范介绍1. Vite 文件目录结构 Vue3 并没有强制规定文件目录结构,开发者可以按照自己喜欢的方式组织代码。不过,通常情况下,我们会按照以下方式组织文件目录: ├── public │ …...

Leetcode 剑指 Offer II 016. 不含重复字符的最长子字符串
题目难度: 中等 原题链接 今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复 剑指offer2 就能看到该系列当前连载的所有文章了, 记得关注哦~ 题目描述 给定一个字符串 s ,请你找出其中不含有重复字符的最长…...

TCP 的演化史-sack 与 reordering metric
就着 TCP 本身说事,而不是高谈阔论关于它是如何不合时宜,然后摆出一个更务虚的更新。 从一个 case 开始。 按照现在 Linux TCP(遵守 RFC) 实现,以下是一个将会导致 reordering 更新的 sack 序列: 考虑一种情况,这两个…...

【Spring6】| Spring的入门程序、集成Log4j2日志框架
目录 一:Spring的入门程序 1. Spring的下载 2. Spring的jar文件 3. 第一个Spring程序 4. 第一个Spring程序详细剖析 5. Spring6启用Log4j2日志框架 一:Spring的入门程序 1. Spring的下载 官网地址:https://spring.io/ 官网地址&…...
)
包子凑数(完全背包)
小明几乎每天早晨都会在一家包子铺吃早餐。 他发现这家包子铺有 N 种蒸笼,其中第 i种蒸笼恰好能放 Ai 个包子。 每种蒸笼都有非常多笼,可以认为是无限笼。 每当有顾客想买 X 个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
