考研数学中放缩法和无穷项求和
考研数学放缩法和无穷项求和
- 放缩法专题
- 例子1
- 例子2
- 例子3
- 例子4
- 例子5
放缩法专题
本文以例子为切入,对一些常用的放缩方法进行总结归纳,以期让读者对相关问题有一定的应对手段。
例子1
问题:2020年高数甲,选择题第1题。
lim n → + ∞ ( 2 n 2 + 4 n 2 + 1 + ⋯ + 2 n n 2 + n + 1 ) \lim_{n\to+\infty}\left( \frac{2}{n^2}+\frac{4}{n^2+1}+\cdots + \frac{2n}{n^2+n+1}\right) n→+∞lim(n22+n2+14+⋯+n2+n+12n)
解答:这个问题比较简单,只要注意到分母在 n → + ∞ n\to+\infty n→+∞的过程中, n 2 n^2 n2占主导项,那么就可以把分母统一起来,可以缩小到 n 2 n^2 n2,也可以放大到 n 2 + n + 1 n^2+n+1 n2+n+1。
分母统一后注意到 2 + 4 + ⋯ + 2 n = 2 × n ( n + 1 ) 2 2+4+\cdots + 2n=2\times\frac{n(n+1)}{2} 2+4+⋯+2n=2×2n(n+1),那么极限就是分子和分母 n 2 n^2 n2项系数之比。
归纳总结:
- 放缩的项,尽量是不重要的项。
类似题目:
- 2017年高数甲,选择题第2题;2013年高数甲,选择题第2题。
例子2
问题:2019年高数甲,选择题第一题。
求极限:
lim n → ∞ [ ( 1 + 1 2 ! + 1 3 ! + ⋯ 1 n ! ) + ( 1 1 × 3 + 1 3 × 5 + ⋯ 1 ( 2 n − 1 ) × ( 2 n + 1 ) ) ] \lim_{n\to\infty}\left[\left(1+\frac{1}{2!}+\frac{1}{3!}+\cdots \frac{1}{n!}\right)+\left(\frac{1}{1\times 3}+\frac{1}{3\times 5}+\cdots \frac{1}{(2n-1)\times (2n+1)}\right)\right] n→∞lim[(1+2!1+3!1+⋯n!1)+(1×31+3×51+⋯(2n−1)×(2n+1)1)]
A. e − 1 2 e-\frac{1}{2} e−21
B. 5 2 \frac{5}{2} 25
C. e + 1 2 e+\frac{1}{2} e+21
D. 7 2 \frac{7}{2} 27
解答:这个问题作为选择题比较简单,要直接求极限则很复杂。
首先注意到,中括号中,两项极限肯定都存在。因为这两个求和项都比调和级数小,所以一定各自收敛。
那再看第二项 ( 1 1 × 3 + 1 3 × 5 + ⋯ 1 ( 2 n − 1 ) × ( 2 n + 1 ) ) \left(\frac{1}{1\times 3}+\frac{1}{3\times 5}+\cdots \frac{1}{(2n-1)\times (2n+1)}\right) (1×31+3×51+⋯(2n−1)×(2n+1)1),这里很明显应该用裂项消除来做,只要注意到:
1 ( 2 n − 1 ) ( 2 n + 1 ) = 1 2 ( 1 2 n − 1 − 1 2 n + 1 ) \frac{1}{(2n-1)(2n+1)}=\frac{1}{2}\left(\frac{1}{2n-1}-\frac{1}{2n+1}\right) (2n−1)(2n+1)1=21(2n−11−2n+11)
那么,裂项就可以化成:
1 2 ( 1 − 1 3 + 1 3 − 1 5 + ⋯ − 1 2 n + 1 ) \frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\cdots-\frac{1}{2n+1}\right) 21(1−31+31−51+⋯−2n+11)
很显然,此项的极限是 1 2 \frac{1}{2} 21。
再看第一项,乍一看这是一个很难的极限,但注意到选项中出现了 e e e,可以意识到它可能和两个重要极限中的
lim n → ∞ ( 1 + 1 n ) n \lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n n→∞lim(1+n1)n
曾使用过此项:
lim n → ∞ ( 1 + 1 2 ! + 1 3 ! + ⋯ 1 n ! ) \lim_{n\to\infty}\left(1+\frac{1}{2!}+\frac{1}{3!}+\cdots \frac{1}{n!}\right) n→∞lim(1+2!1+3!1+⋯n!1)
这里回顾一下证明重要极限的过程就可以理解了,直接用二项式定理公式展开:
( 1 + 1 n ) n = 1 + ( n 1 ) 1 n + ( n 2 ) 1 n 2 + ⋯ + ( n n ) 1 n n = 1 + n 1 ! ⋅ 1 n + n ( n − 1 ) 2 ! ⋅ 1 n 2 + ⋯ + n ( n − 1 ) ( n − 2 ) ⋯ ( n − n + 1 ) n ! ⋅ 1 n n = 1 + 1 + 1 2 ! ⋅ n ( n − 1 ) n 2 + ⋯ + 1 n ! ⋅ n ( n − 1 ) ( n − 2 ) ⋯ ( n − n + 1 ) n n ≤ 1 + 1 + 1 2 ! + 1 3 ! + ⋯ 1 n ! \begin{aligned} \left(1+\frac{1}{n}\right)^n&=1+{n\choose 1}\frac{1}{n}+{n\choose 2}\frac{1}{n^2}+\cdots +{n\choose n}\frac{1}{n^n} \\ &= 1+\frac{n}{1!}\cdot \frac{1}{n}+\frac{n(n-1)}{2!}\cdot \frac{1}{n^2}+\cdots+\frac{n(n-1)(n-2)\cdots (n-n+1)}{n!}\cdot \frac{1}{n^n} \\ &=1+1+\frac{1}{2!}\cdot \frac{n(n-1)}{n^2}+\cdots+\frac{1}{n!}\cdot \frac{n(n-1)(n-2)\cdots (n-n+1)}{n^n} \\ &\le 1+1+\frac{1}{2!}+\frac{1}{3!}+\cdots \frac{1}{n!} \end{aligned} (1+n1)n=1+(1n)n1+(2n)n21+⋯+(nn)nn1=1+1!n⋅n1+2!n(n−1)⋅n21+⋯+n!n(n−1)(n−2)⋯(n−n+1)⋅nn1=1+1+2!1⋅n2n(n−1)+⋯+n!1⋅nnn(n−1)(n−2)⋯(n−n+1)≤1+1+2!1+3!1+⋯n!1
因此
lim n → ∞ ( 1 + 1 2 ! + 1 3 ! + ⋯ 1 n ! ) ≥ e − 1 \lim_{n\to\infty}\left(1+\frac{1}{2!}+\frac{1}{3!}+\cdots \frac{1}{n!}\right)\ge e-1 n→∞lim(1+2!1+3!1+⋯n!1)≥e−1
即使不记得此式,也应该记得重要极限的证明过程中,怎么确定上限的,那就是一个经典的放缩:
只需要注意到,函数的增长速度 2 n − 1 < n ! < n n 2^{n-1}<n!<n^n 2n−1<n!<nn,将阶乘放缩到 n n n^n nn是没用的,因为 ∑ n = 1 ∞ 1 n n \sum_{n=1}^{\infty}\frac{1}{n^n} ∑n=1∞nn1求和仍然不好求,放缩到 2 n − 1 2^{n-1} 2n−1可以凑等比数列。可以得到:
lim n → ∞ ( 1 + 1 2 ! + 1 3 ! + ⋯ 1 n ! ) < lim n → ∞ ( 1 + 1 2 1 + 1 2 2 + ⋯ + 1 2 n − 1 ) = 2 \lim_{n\to\infty}\left(1+\frac{1}{2!}+\frac{1}{3!}+\cdots \frac{1}{n!}\right) < \lim_{n\to\infty}\left(1+\frac{1}{2^1}+\frac{1}{2^2}+\cdots +\frac{1}{2^{n-1}}\right)=2 n→∞lim(1+2!1+3!1+⋯n!1)<n→∞lim(1+211+221+⋯+2n−11)=2
即便 2 n 2^n 2n是能想象到的最接近 n ! n! n!的函数,但两者实际上差距仍然很大,所以这两个极限不相等,但这个不等关系已经可以排除出正确答案了。因为可以得到原式子一定小于 2 + 1 2 = 5 2 2+\frac{1}{2}=\frac{5}{2} 2+21=25,只有A选项符合这个大小。
归纳总结
- 放缩的原则,放缩前后尽量接近;
- 放缩后是为了方便求值,有时不必保证放缩前后极限相等,不等关系也可以选出正确答案;
- 要对一些书上经典的证明有所了解,很多考试的技巧都在书中经典证明中出现过。
例子3
问题:2015年第二大题,计算
lim n → ∞ 1 n ( 1 + sin π n + 1 + sin 2 π n + ⋯ + 1 + sin n π n ) \lim_{n\to \infty}\frac{1}{n}\left(\sqrt{1+\sin{\frac{\pi}{n}}}+\sqrt{1+\sin{\frac{2\pi}{n}}}+\cdots + \sqrt{1+\sin{\frac{n\pi}{n}}}\right) n→∞limn1(1+sinnπ+1+sinn2π+⋯+1+sinnnπ)
解答:这个题目看上去也是无穷级数的累加,进行适当放缩。但实际上注意到 1 n \frac{1}{n} n1,应当把此极限化为定积分来计算。
归纳总结
- 有些无穷级数累加的极限,不要盲目用放缩法,能否化为定积分更容易判断。
例子4
问题:2004年第1大题,计算
lim n → ∞ sin 1 + sin 1 2 + ⋯ + sin 1 n n \lim_{n\to\infty}\sqrt[n]{\sin1+\sin\frac{1}{2}+\cdots +\sin\frac{1}{n}} n→∞limnsin1+sin21+⋯+sinn1
解答:首先检验是否可以定积分计算,定积分计算必然需要找出 d x = 1 n dx=\frac{1}{n} dx=n1和定义变量 x x x取值的 i n \frac{i}{n} ni,x是等间距变化才行,而本题目中虽然可以构造 1 / n 1/n 1/n,但 sin \sin sin内部的变化不是等间距的,因此不能用定积分。
然后检查是否可以裂项或使用三角函数等性质,制造连锁的反应,以直接求和出来,但不管和差化积、倍角公式还是乘 cos \cos cos函数都不能实现此效果。三角函数乘积时容易用性质来做一些操作,但这里没有办法化乘积。
最后考虑放缩,如果了解一个常用的结论(证明方法也很经典,可以用均值不等式):
lim n → ∞ n n = 1 \lim_{n\to\infty}\sqrt[n]{n}=1 n→∞limnn=1
那么对放缩会有一个提前的意识:即便开 n n n次根号下是一个函数 n n n,增长率是线性的,开 n n n次方结果仍会收到 1 1 1。而根号下的求和实际上肯定不如 n n n的。因此基本可以断定,这个极限结果必然是 1 1 1,为验证此观点,放缩可以大胆点:
1 < sin 1 + sin 1 2 + ⋯ + sin 1 n < n 1<\sin1+\sin\frac{1}{2}+\cdots +\sin\frac{1}{n}<n 1<sin1+sin21+⋯+sinn1<n
因此:
lim n → ∞ 1 n < lim n → ∞ sin 1 + sin 1 2 + ⋯ + sin 1 n n < lim n → ∞ n n \lim_{n\to\infty}\sqrt[n]{1}<\lim_{n\to\infty}\sqrt[n]{\sin1+\sin\frac{1}{2}+\cdots +\sin\frac{1}{n}}<\lim_{n\to\infty}\sqrt[n]{n} n→∞limn1<n→∞limnsin1+sin21+⋯+sinn1<n→∞limnn
总结:
- 要了解一些常用的极限,判断要计算的级数的增长数量级,对放缩有一定的预估。
- 有些操作如开 n n n次方 x n \sqrt[n]{x} nx,本身会将很大范围内的函数收缩到 1 1 1,这时不妨放缩大胆点。
例子5
问题:2002年第一题,求解
lim n → ∞ cos 1 2 cos 1 4 ⋯ cos 1 2 n \lim_{n\to\infty}\cos\frac{1}{2}\cos\frac{1}{4}\cdots \cos\frac{1}{2^n} n→∞limcos21cos41⋯cos2n1
解答:看到三角函数,各个取值是2倍关系,应当立即想到倍角公式,这里只要乘以 sin 1 2 n \sin\frac{1}{2^n} sin2n1,即可知道如何做,当然别忘了额外乘了什么,就要除以什么。
相关文章:

考研数学中放缩法和无穷项求和
考研数学放缩法和无穷项求和 放缩法专题例子1例子2例子3例子4例子5 放缩法专题 本文以例子为切入,对一些常用的放缩方法进行总结归纳,以期让读者对相关问题有一定的应对手段。 例子1 问题:2020年高数甲,选择题第1题。 lim …...

计算机网络常识
文章目录 1、HTTP2、HTTP状态码1xx(信息性状态码):2xx(成功状态码):3xx(重定向状态码):4xx(客户端错误状态码):5xx(服务器…...
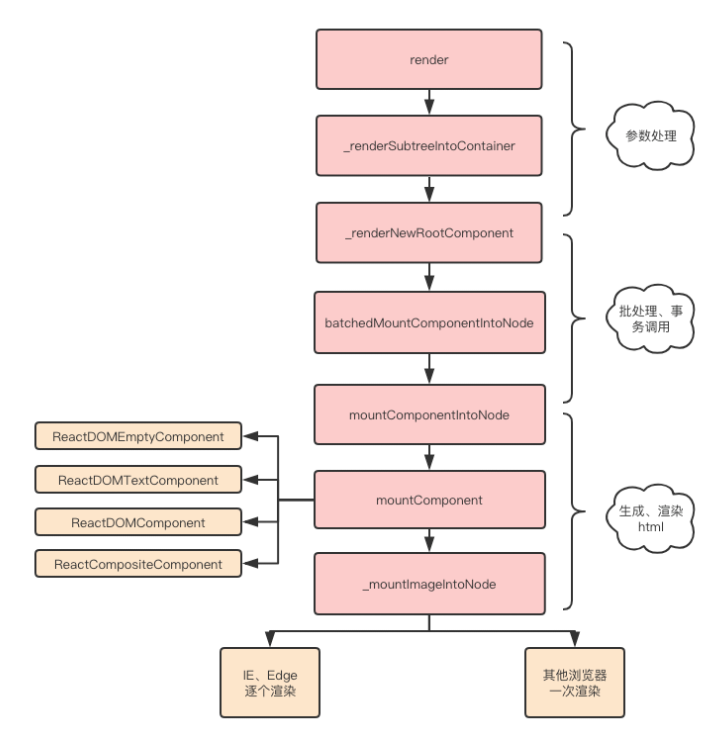
React之Jsx如何转换成真实DOM
一、是什么 react通过将组件编写的JSX映射到屏幕,以及组件中的状态发生了变化之后 React会将这些「变化」更新到屏幕上 在前面文章了解中,JSX通过babel最终转化成React.createElement这种形式,例如: <div>< img src&q…...

OpenCV学习(六)——图像算术运算(加法、融合与按位运算)
图像算术运算 6. 图像算术运算6.1 图像加法6.2 图像融合6.3 按位运算 6. 图像算术运算 6.1 图像加法 OpenCV加法是饱和运算Numpy加法是模运算 import cv2 import numpy as npx np.uint8([250]) y np.uint8([10])# OpenCV加法 print(cv2.add(x, y)) # 25010 260 > 255…...

如何做好一次代码审查,什么样是一次优秀的代码审查,静态代码分析工具有哪些
代码审查是确保代码质量、提升团队协作效率、分享知识和技能的重要过程。以下是进行优秀代码审查的一些指南: 如何做好代码审查: 理解代码的背景和目的: 在开始审查前,确保你了解这次提交的背景和目的,这有助于更准确…...

【Android】一个contentResolver引起的内存泄漏问题分析
长时间的压力测试后,系统发生了重启,报错log如下 JNI ERROR (app bug): global reference table overflow (max51200) global reference table overflow的log 08-08 04:11:53.052912 973 3243 F zygote64: indirect_reference_table.cc:256] JNI ER…...
2023年正版win10/win11系统安装教学(纯净版)
第一步:准备一个8G容量以上的U盘。 注意,在制作系统盘时会格式化U盘,所以最好准备个空U盘,防止资料丢失。 第二步:制作系统盘。 安装win10 进入windows官网 官网win10下载地址:https://www.microsoft.c…...

系统架构设计师-第11章-未来信息综合技术-软考学习笔记
未来信息综合技术是指近年来新技术发展而提出的一些新概念、新知识、新产品 信息物理系统(CPS ) ,人工智能( A l) ,机器人、边缘计算、数字孪生、云计算和大数据等技术 信息物理系统技术概述 信息物理系统的概念 信息物理系统是控制系统、嵌入式系统…...
方法详解)
Python __new__()方法详解
__new__() 是一种负责创建类实例的静态方法,它无需使用 staticmethod 装饰器修饰,且该方法会优先 __init__() 初始化方法被调用。 一般情况下,覆写 __new__() 的实现将会使用合适的参数调用其超类的 super().__new__(),并在返回之…...

虹科 | 解决方案 | 汽车示波器 索赔管理方案
索赔管理 Pico汽车示波器应用于主机厂/供应商与服务店/4S店的协作,实现产品索赔工作的高效管理;同时收集的故障波形数据,便于日后的产品优化和改进 故障记录 在索赔申请过程中,Pico汽车示波器的数据记录功能可以用于捕捉故障时的…...

详解Jmeter中的BeanShell脚本
BeanShell是一种完全符合Java语法规范的脚本语言,并且又拥有自己的一些语法和方法,所以它和java是可以无缝衔接的,学了Java的一些基本语法后,就可以来在Jmeter中写写BeanShell脚本了 在利用jmeter进行接口测试或者性能测试的时候,…...

前端和后端 优化
1.前端资源优化 1.1 html结构优化 保证简洁、清晰的html结构,减少或避免多余的html标签 使用HTML5的web语义化标签,结构清晰且利于seo css文件在head中引入,js文件放在body底部引入,这样做可以防止阻塞。另外如果有需要提前加载的…...

C++编译与运行:其二、编译期和运行期的区别
C的编译分为四步,最终生成一个可执行文件。 C的运行,就是将可执行文件交给操作系统,按照机器码逐步执行,运行功能。 先看一个非常非常有趣的例子: class Father{ public:virtual void f(){cout<<"I am fat…...
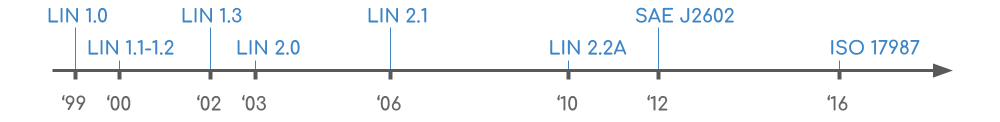
汽车电子专有名词与相应技术
1.EEA (Electronic & Electrical Architecture 电子电气架构) EEA在宏观上概括为物理架构与逻辑架构的结合,微观上通过众多电子元器件的协同配合,或集成式或分布式的系统级电子电气架构,具体详见专栏 新能源汽车电…...

idea 没加载 provided的包
目录 前言解决方案 前言 我的版本是IntelliJ IDEA 2022.1.4 (Community Edition),本地调试不知道为什么不加载provided的包。后来找到这篇文章https://youtrack.jetbrains.com/issue/IDEA-107048才知道这是个bug。不知道其他版本会不会出现这种问题。 解决方案 我…...

Hover:借贷新势力崛起,在经验与创新中找寻平衡
复苏中的Cosmos 如果让我选择一个最我感到可惜的区块链项目,我会选择Cosmos。 Cosmos最早提出并推动万链互联的概念,希望打通不同链之间的孤岛,彼时和另一个天王项目Polkadot号称跨链双雄。其跨链技术允许不同的区块链网络互相通信…...

软件设计原则-依赖倒置原则讲解以及代码示例
依赖倒置原则 一,介绍 1.前言 依赖倒置原则(Dependency Inversion Principle,DIP)是面向对象设计中的一个重要原则,由Robert C. Martin提出。 依赖倒置原则的核心思想是:高层模块不应该依赖于低层模块&…...

Linux--进程替换
1.什么是进程替换 在fork函数之后,父子进程各自执行代码的一部分,但是如果子进程想要执行一份全新的程序呢? 通过进程替换来完成,进程替换就是父子进程代码发生写时拷贝,子进程执行自己的功能。 程序替换就是通过特定的…...
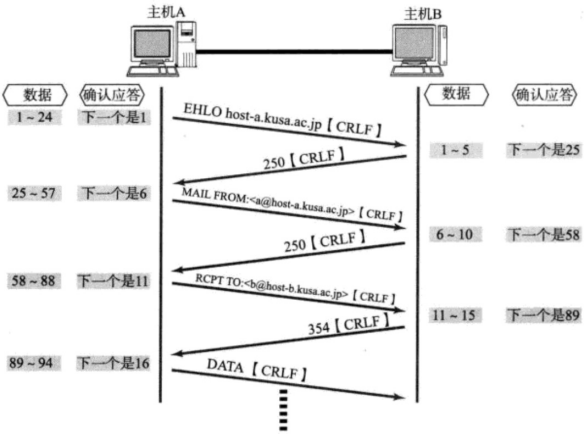
【计算机网络】TCP协议
文章目录 1. TCP报文的结构2. TCP的发送缓冲区和接收缓冲区3. 确保可靠性序列号和确认序列号确认应答超时重传连接管理1️⃣三次握手建立连接2️⃣四次挥手断开连接 4. 提高性能流量控制滑动窗口拥塞控制延迟应答捎带应答 5. 面向字节流6. TCP/UDP对比 概念:TCP&…...

机器学习数据集:Kaggle
什么是Kaggle? Kaggle成立于2010年,是一个进行数据发掘和预测竞赛的在线平台。从公司的角度来讲,可以提供一些数据,进而提出一个实际需要解决的问题;从参赛者的角度来讲,他们将组队参与项目,针…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

C++ 类基础:封装、继承、多态与多线程模板实现
前言 C 是一门强大的面向对象编程语言,而类(Class)作为其核心特性之一,是理解和使用 C 的关键。本文将深入探讨 C 类的基本特性,包括封装、继承和多态,同时讨论类中的权限控制,并展示如何使用类…...

C# WPF 左右布局实现学习笔记(1)
开发流程视频: https://www.youtube.com/watch?vCkHyDYeImjY&ab_channelC%23DesignPro Git源码: GitHub - CSharpDesignPro/Page-Navigation-using-MVVM: WPF - Page Navigation using MVVM 1. 新建工程 新建WPF应用(.NET Framework) 2.…...
