学习笔记:Splay
Splay
定义
Splay 树, 或 伸展树,是一种平衡二叉查找树,它通过 Splay/伸展操作 不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质,能够在均摊 O ( log n ) O(\log n) O(logn) 时间内完成插入,查找和删除操作,并且保持平衡而不至于退化为链。
Splay 树由 Daniel Sleator 和 Robert Tarjan 于 1985 年发明。
结构
节点维护信息
x tot fa[i] ch[i][0/1] val[i] cnt[i] sz[i]
根节点编号 节点个数 父亲 左右儿子编号 节点权值 权值出现次数 子树大小
struct Splay{
int fa, ch[2], val, cnt, siz;
}tree[MAXN];
操作
基本操作
maintain(x):在改变节点位置后,将节点 x x x 的 size \text{size} size 更新。
get(x):判断节点 x x x 是父亲节点的左儿子还是右儿子。
clear(x):销毁节点 x x x。
void maintain(int x){
tree[x].siz = tree[tree[x].ch[0]].siz + tree[tree[x].ch[1]].siz + tree[x].cnt;
}
bool get(int x){
if(x == tree[tree[x].fa].ch[1])return true;
else return false;
}
void clear(int x){
tree[tree[x].ch[0]].siz = 0;
tree[tree[x].ch[1]].siz = 0;
tree[x].fa = 0;tree[x].val = 0;
tree[x].cnt = 0;tree[x].siz = 0;
}
旋转操作
为了使 Splay 保持平衡而进行旋转操作,旋转的本质是将某个节点上移一个位置。
旋转需要保证:
整棵 Splay 的中序遍历不变(不能破坏二叉查找树的性质)。
受影响的节点维护的信息依然正确有效。
root 必须指向旋转后的根节点。
在 Splay 中旋转分为两种:左旋和右旋。
过程
具体分析旋转步骤(假设需要旋转的节点为 x x x,其父亲为 y y y,以右旋为例)
将 y y y 的左儿子指向 x x x 的右儿子,且 x x x 的右儿子(如果 x x x 有右儿子的话)的父亲指向 y y y;ch[y][0] = ch[x][1];fa[ch[x][1]] = y;
将 x x x 的右儿子指向 y y y,且 y y y 的父亲指向 x x x;ch[x][chk^1] = y;fa[y] = x;
如果原来的 y y y 还有父亲 z z z,那么把 z z z 的某个儿子(原来 y y y 所在的儿子位置)指向 x x x,且 x x x 的父亲指向 z z z。fa[x] = z;if(z)ch[z][y == ch[z][1]] = x;
实现
void maintain(int x){
tree[x].siz = tree[tree[x].ch[0]].siz + tree[tree[x].ch[1]].siz + tree[x].cnt;
}
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
Splay 操作
Splay 操作规定:每访问一个节点 x x x 后都要强制将其旋转到根节点。
Splay 操作即对 x x x 做一系列的 Splay 步骤。每次对 x x x 做一次 splay 步骤, x x x 到根节点的距离都会更近。定义 p p p 为 x x x 的父节点。Splay 步骤有三种,具体分为六种情况:
实现
void maintain(int x){
tree[x].siz = tree[tree[x].ch[0]].siz + tree[tree[x].ch[1]].siz + tree[x].cnt;
}
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
插入操作
过程
插入操作是一个比较复杂的过程,具体步骤如下(假设插入的值为 k k k):
如果树空了,则直接插入根并退出。
如果当前节点的权值等于 k k k 则增加当前节点的大小并更新节点和父亲的信息,将当前节点进行 Splay 操作。
否则按照二叉查找树的性质向下找,找到空节点就插入即可(请不要忘记 Splay 操作)。
实现
void maintain(int x){
tree[x].siz = tree[tree[x].ch[0]].siz + tree[tree[x].ch[1]].siz + tree[x].cnt;
}
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
void insert(int k){
if(!root){
tree[++tot].val = k;tree[tot].cnt++;
root = tot;maintain(root);return;
}
int cur = root, f = 0;
while(true){
if(tree[cur].val == k){
tree[cur].cnt++;
maintain(cur);maintain(f);
splay(cur);break;
}
f = cur;cur = tree[f].ch[tree[f].val < k];
if(!cur){
tree[++tot].val = k;tree[tot].cnt++;tree[tot].fa = f;
tree[f].ch[tree[f].val < k] = tot;
maintain(tot);maintain(f);splay(tot);break;
}
}
}
查询 x 的排名
过程
根据二叉查找树的定义和性质,显然可以按照以下步骤查询 x x x 的排名:
如果 x x x 比当前节点的权值小,向其左子树查找。
如果 x x x 比当前节点的权值大,将答案加上左子树( s i z e size size)和当前节点( c n t cnt cnt)的大小,向其右子树查找。
如果 x x x 与当前节点的权值相同,将答案加 1 1 1 并返回。
注意最后需要进行 Splay 操作。
实现
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
int getrank(int k){
int res = 0, cur = root;
while(true){
if(k < tree[cur].val)cur = tree[cur].ch[0];
else{
res += tree[tree[cur].ch[0]].siz;
if(k == tree[cur].val){splay(cur);return res + 1;}
res += tree[cur].cnt;cur = tree[cur].ch[1];
}
}
}
查询排名 x 的数
过程
设 k k k 为剩余排名,具体步骤如下:
如果左子树非空且剩余排名 k k k 不大于左子树的大小 s i z e size size,那么向左子树查找。
否则将 k k k 减去左子树的和根的大小。如果此时 k k k 的值小于等于 0 0 0,则返回根节点的权值,否则继续向右子树查找。
实现
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
int getval(int k){
int cur = root;
while(true){
if(tree[cur].ch[0] && k <= tree[tree[cur].ch[0]].siz)cur = tree[cur].ch[0];
else{k -= tree[tree[cur].ch[0]].siz + tree[cur].cnt;
if(k <= 0){splay(cur);return tree[cur].val;}
cur = tree[cur].ch[1];
}
}
}
查询前驱
过程
前驱定义为小于 x x x 的最大的数,那么查询前驱可以转化为:将 x x x 插入(此时 x x x 已经在根的位置了),前驱即为 x x x 的左子树中最右边的节点,最后将 x x x 删除即可。
实现
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
int getpre(){
int cur = tree[root].ch[0];
if(!cur)return cur;
while(tree[cur].ch[1])cur = tree[cur].ch[1];
splay(cur);return cur;
}
查询后继
过程
后继定义为大于 x x x 的最小的数,查询方法和前驱类似: x x x 的右子树中最左边的节点。
实现
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
int getnxt(){
int cur = tree[root].ch[1];
if(!cur)return cur;
while(tree[cur].ch[0])cur = tree[cur].ch[0];
splay(cur);return cur;
}
合并两棵树
过程
合并两棵 Splay 树,设两棵树的根节点分别为 x x x 和 y y y,那么我们要求 x x x 树中的最大值小于 y y y 树中的最小值。合并操作如下:
如果 x x x 和 y y y 其中之一或两者都为空树,直接返回不为空的那一棵树的根节点或空树。
否则将 x x x 树中的最大值 Splay \operatorname{Splay} Splay 到根,然后把它的右子树设置为 y y y 并更新节点的信息,然后返回这个节点。
删除操作
过程
删除操作也是一个比较复杂的操作,具体步骤如下:
首先将 x x x 旋转到根的位置。
如果 c n t [ x ] > 1 cnt[x]>1 cnt[x]>1(有不止一个 x x x),那么将 c n t [ x ] cnt[x] cnt[x] 减 1 1 1 并退出。
否则,合并它的左右两棵子树即可。
实现
void maintain(int x){
tree[x].siz = tree[tree[x].ch[0]].siz + tree[tree[x].ch[1]].siz + tree[x].cnt;
}
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void clear(int x){
tree[tree[x].ch[0]].siz = 0;
tree[tree[x].ch[1]].siz = 0;
tree[x].fa = 0;tree[x].val = 0;
tree[x].cnt = 0;tree[x].siz = 0;
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
int getrank(int k){
int res = 0, cur = root;
while(true){
if(k < tree[cur].val)cur = tree[cur].ch[0];
else{
res += tree[tree[cur].ch[0]].siz;
if(k == tree[cur].val){splay(cur);return res + 1;}
res += tree[cur].cnt;cur = tree[cur].ch[1];
}
}
}
int getpre(){
int cur = tree[root].ch[0];
if(!cur)return cur;
while(tree[cur].ch[1])cur = tree[cur].ch[1];
splay(cur);return cur;
}
void remove(int k){
getrank(k);
if(tree[root].cnt > 1){tree[root].cnt–;maintain(root);return;}
if(!tree[root].ch[0] && !tree[root].ch[1]){clear(root);root = 0;return;}
if(!tree[root].ch[0]){
int cur = root;root = tree[root].ch[1];
tree[root].fa = 0;clear(cur);return;
}
if(!tree[root].ch[1]){
int cur = root;root = tree[root].ch[0];
tree[root].fa = 0;clear(cur);return;
}
int cur = root, x = getpre();
tree[tree[cur].ch[1]].fa = root;
tree[root].ch[1] = tree[cur].ch[1];
clear(cur);maintain(root);
}
实现
#include
#define MAXN 100005
using namespace std;
int n, opt, x, root, tot;
struct splay{
int fa, ch[2], val, cnt, siz;
}tree[MAXN];
int read(){
int t = 1, x = 0;char ch = getchar();
while(!isdigit(ch)){if(ch == ‘-’)t = -1;ch = getchar();}
while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * t;
}
void write(int x){
if(x < 0){putchar(‘-’);x = -x;}
if(x >= 10)write(x/ 10);
putchar(x % 10 ^ 48);
}
void maintain(int x){
tree[x].siz = tree[tree[x].ch[0]].siz + tree[tree[x].ch[1]].siz + tree[x].cnt;
}
bool get(int x){
return x == tree[tree[x].fa].ch[1];
}
void clear(int x){
tree[tree[x].ch[0]].siz = 0;
tree[tree[x].ch[1]].siz = 0;
tree[x].fa = 0;tree[x].val = 0;
tree[x].cnt = 0;tree[x].siz = 0;
}
void rotate(int x){
int y = tree[x].fa, z = tree[y].fa, chk = get(x);
tree[y].ch[chk] = tree[x].ch[chk ^ 1];
if(tree[x].ch[chk ^ 1])tree[tree[x].ch[chk ^ 1]].fa = y;
tree[x].ch[chk ^ 1] = y;
tree[y].fa = x;tree[x].fa = z;
if(z != 0)tree[z].ch[y == tree[z].ch[1]] = x;
maintain(x);maintain(y);
}
void splay(int x){
for(int f = tree[x].fa ; f = tree[x].fa, f ; rotate(x))
if(tree[f].fa)rotate(get(x) == get(f) ? f : x);
root = x;
}
void insert(int k){
if(!root){
tree[++tot].val = k;tree[tot].cnt++;
root = tot;maintain(root);return;
}
int cur = root, f = 0;
while(true){
if(tree[cur].val == k){
tree[cur].cnt++;
maintain(cur);maintain(f);
splay(cur);break;
}
f = cur;cur = tree[f].ch[tree[f].val < k];
if(!cur){
tree[++tot].val = k;tree[tot].cnt++;tree[tot].fa = f;
tree[f].ch[tree[f].val < k] = tot;
maintain(tot);maintain(f);splay(tot);break;
}
}
}
int getrank(int k){
int res = 0, cur = root;
while(true){
if(k < tree[cur].val)cur = tree[cur].ch[0];
else{
res += tree[tree[cur].ch[0]].siz;
if(k == tree[cur].val){splay(cur);return res + 1;}
res += tree[cur].cnt;cur = tree[cur].ch[1];
}
}
}
int getval(int k){
int cur = root;
while(true){
if(tree[cur].ch[0] && k <= tree[tree[cur].ch[0]].siz)cur = tree[cur].ch[0];
else{k -= tree[tree[cur].ch[0]].siz + tree[cur].cnt;
if(k <= 0){splay(cur);return tree[cur].val;}
cur = tree[cur].ch[1];
}
}
}
int getpre(){
int cur = tree[root].ch[0];
if(!cur)return cur;
while(tree[cur].ch[1])cur = tree[cur].ch[1];
splay(cur);return cur;
}
int getnxt(){
int cur = tree[root].ch[1];
if(!cur)return cur;
while(tree[cur].ch[0])cur = tree[cur].ch[0];
splay(cur);return cur;
}
void remove(int k){
getrank(k);
if(tree[root].cnt > 1){tree[root].cnt–;maintain(root);return;}
if(!tree[root].ch[0] && !tree[root].ch[1]){clear(root);root = 0;return;}
if(!tree[root].ch[0]){
int cur = root;root = tree[root].ch[1];
tree[root].fa = 0;clear(cur);return;
}
if(!tree[root].ch[1]){
int cur = root;root = tree[root].ch[0];
tree[root].fa = 0;clear(cur);return;
}
int cur = root, x = getpre();
tree[tree[cur].ch[1]].fa = root;
tree[root].ch[1] = tree[cur].ch[1];
clear(cur);maintain(root);
}
int main(){
n = read();
for(int i = 1 ; i <= n ; i ++){
opt = read();x = read();
switch(opt){
case 1:insert(x);break;
case 2:remove(x);break;
case 3:write(getrank(x));putchar(‘\n’);break;
case 4:write(getval(x));putchar(‘\n’);break;
case 5:insert(x);write(tree[getpre()].val);putchar(‘\n’);remove(x);break;
case 6:insert(x);write(tree[getnxt()].val);putchar(‘\n’);remove(x);break;
default:break;
}
}
return 0;
}
Splay 操作的时间复杂度
因为 zig 和 zag 是 对称 操作,我们只需要对 zig,zig−zig,zig−zag 操作分析复杂度。采用势能分析,定义一个 n n n 个节点的 Splay 树进行了 m m m 次 Splay 步骤。可记 w ( x ) = [ log ( size ( x ) ) ] w(x)=[\log(\operatorname{size}(x))] w(x)=[log(size(x))], 定义势能函数为 φ = ∑ w ( x ) \varphi =\sum w(x) φ=∑w(x), φ ( 0 ) ≤ n log n \varphi (0) \leq n \log n φ(0)≤nlogn,在第 i i i 次操作后势能为 φ ( i ) \varphi (i) φ(i), 则我们只需要求出初始势能和每次的势能变化量的和即可。
由此可见,三种 Splay 步骤的势能全部可以缩放为 ≤ 3 ( w ′ ( x ) − w ( x ) ) \leq 3(w'(x)−w(x)) ≤3(w′(x)−w(x)). 令 w ( n ) ( x ) = w ′ ( n − 1 ) ( x ) w^{(n)}(x)=w'^{(n-1)}(x) w(n)(x)=w′(n−1)(x), w ( 0 ) ( x ) = w ( x ) w^{(0)}(x)=w(x) w(0)(x)=w(x), 假设 Splay 操作一次依次访问了 x 1 , x 2 , ⋯ , x n x_{1}, x_{2}, \cdots, x_{n} x1,x2,⋯,xn, 最终 x 1 x_{1} x1 成为根节点,我们可以得到:
3 ( ∑ i = 0 n − 2 ( w ( i + 1 ) ( x 1 ) − w ( i ) ( x 1 ) ) + w ( n ) − w ( n − 1 ) ( x 1 ) ) + 1 = 3 ( w ( n ) − w ( x 1 ) ) + 1 ≤ log n \begin{aligned} 3\left(\sum_{i=0}^{n-2}\left(w^{(i+1)}(x_{1})-w^{(i)}(x_{1})\right)+w(n)−w^{(n-1)}(x_{1})\right)+1 & = 3(w(n)−w(x_{1}))+1 \\ & \leq \log n \end{aligned} 3(i=0∑n−2(w(i+1)(x1)−w(i)(x1))+w(n)−w(n−1)(x1))+1=3(w(n)−w(x1))+1≤logn
继而可得:
∑ i = 1 m ( φ ( m − i + 1 ) − φ ( m − i ) ) + φ ( 0 ) = n log n + m log n \sum_{i=1}^m (\varphi (m-i+1)−\varphi (m−i)) +\varphi (0) = n \log n+m \log n i=1∑m(φ(m−i+1)−φ(m−i))+φ(0)=nlogn+mlogn
因此,对于 n n n 个节点的 Splay 树,做一次 Splay 操作的均摊复杂度为 O ( log n ) O(\log n) O(logn)。因此基于 Splay 的插入,查询,删除等操作的时间复杂度也为均摊 O ( log n ) O(\log n) O(logn)。
相关文章:

学习笔记:Splay
Splay 定义 Splay 树, 或 伸展树,是一种平衡二叉查找树,它通过 Splay/伸展操作 不断将某个节点旋转到根节点,使得整棵树仍然满足二叉查找树的性质,能够在均摊 O ( log n ) O(\log n) O(logn) 时间内完成插入,查…...
JAVA中的垃圾回收器(1)
一)垃圾回收器概述: 1.1)按照线程数来区分: 串行回收指的是在同一时间端内只允许有一个CPU用于执行垃圾回收操作,此时工作线程被暂停,直至垃圾回收工作结束,在诸如单CPU处理器或者较小的应用内存等硬件平台不是特别优越的场合,出行…...
Windows 10/11如何恢复永久删除的文件?
数据丢失在我们的工作生活中经常发生。当你决定清理硬盘或U盘时,你会删除一些文件夹或文件。如果你通过右键单击删除文件,则可以很容易从回收站恢复已删除的文件。但是,如果你按Shift Delete键、清空回收站或删除大于8998MB的大文件夹&#…...
)
【Shell 系列教程】shell介绍(一)
文章目录 前言Shell 脚本Shell 环境第一个shell脚本运行 Shell 脚本有两种方法:1、作为可执行程序2、作为解释器参数 前言 Shell 是一个用 C 语言编写的程序,它是用户使用 Linux 的桥梁。Shell 既是一种命令语言,又是一种程序设计语言。 Sh…...

考研数学中放缩法和无穷项求和
考研数学放缩法和无穷项求和 放缩法专题例子1例子2例子3例子4例子5 放缩法专题 本文以例子为切入,对一些常用的放缩方法进行总结归纳,以期让读者对相关问题有一定的应对手段。 例子1 问题:2020年高数甲,选择题第1题。 lim …...

计算机网络常识
文章目录 1、HTTP2、HTTP状态码1xx(信息性状态码):2xx(成功状态码):3xx(重定向状态码):4xx(客户端错误状态码):5xx(服务器…...
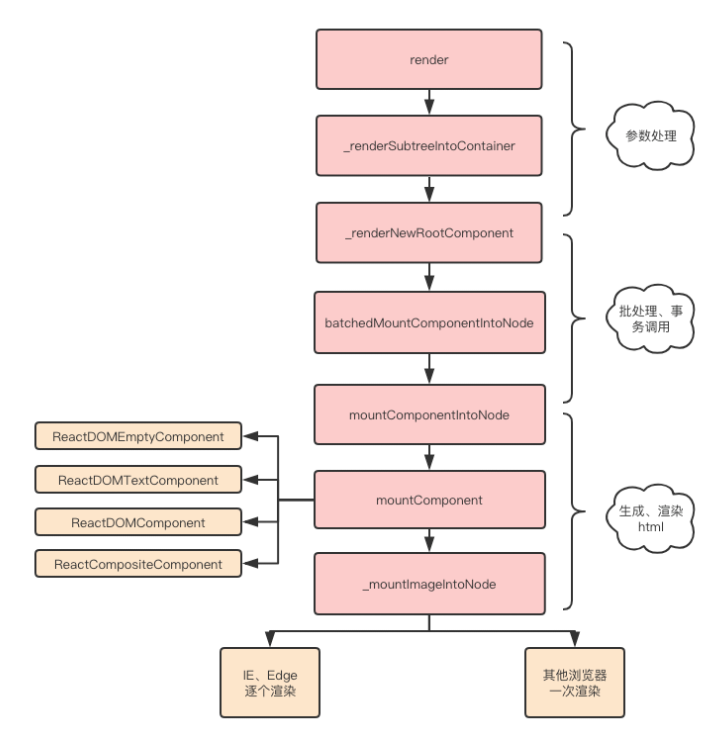
React之Jsx如何转换成真实DOM
一、是什么 react通过将组件编写的JSX映射到屏幕,以及组件中的状态发生了变化之后 React会将这些「变化」更新到屏幕上 在前面文章了解中,JSX通过babel最终转化成React.createElement这种形式,例如: <div>< img src&q…...

OpenCV学习(六)——图像算术运算(加法、融合与按位运算)
图像算术运算 6. 图像算术运算6.1 图像加法6.2 图像融合6.3 按位运算 6. 图像算术运算 6.1 图像加法 OpenCV加法是饱和运算Numpy加法是模运算 import cv2 import numpy as npx np.uint8([250]) y np.uint8([10])# OpenCV加法 print(cv2.add(x, y)) # 25010 260 > 255…...

如何做好一次代码审查,什么样是一次优秀的代码审查,静态代码分析工具有哪些
代码审查是确保代码质量、提升团队协作效率、分享知识和技能的重要过程。以下是进行优秀代码审查的一些指南: 如何做好代码审查: 理解代码的背景和目的: 在开始审查前,确保你了解这次提交的背景和目的,这有助于更准确…...

【Android】一个contentResolver引起的内存泄漏问题分析
长时间的压力测试后,系统发生了重启,报错log如下 JNI ERROR (app bug): global reference table overflow (max51200) global reference table overflow的log 08-08 04:11:53.052912 973 3243 F zygote64: indirect_reference_table.cc:256] JNI ER…...
2023年正版win10/win11系统安装教学(纯净版)
第一步:准备一个8G容量以上的U盘。 注意,在制作系统盘时会格式化U盘,所以最好准备个空U盘,防止资料丢失。 第二步:制作系统盘。 安装win10 进入windows官网 官网win10下载地址:https://www.microsoft.c…...

系统架构设计师-第11章-未来信息综合技术-软考学习笔记
未来信息综合技术是指近年来新技术发展而提出的一些新概念、新知识、新产品 信息物理系统(CPS ) ,人工智能( A l) ,机器人、边缘计算、数字孪生、云计算和大数据等技术 信息物理系统技术概述 信息物理系统的概念 信息物理系统是控制系统、嵌入式系统…...
方法详解)
Python __new__()方法详解
__new__() 是一种负责创建类实例的静态方法,它无需使用 staticmethod 装饰器修饰,且该方法会优先 __init__() 初始化方法被调用。 一般情况下,覆写 __new__() 的实现将会使用合适的参数调用其超类的 super().__new__(),并在返回之…...

虹科 | 解决方案 | 汽车示波器 索赔管理方案
索赔管理 Pico汽车示波器应用于主机厂/供应商与服务店/4S店的协作,实现产品索赔工作的高效管理;同时收集的故障波形数据,便于日后的产品优化和改进 故障记录 在索赔申请过程中,Pico汽车示波器的数据记录功能可以用于捕捉故障时的…...

详解Jmeter中的BeanShell脚本
BeanShell是一种完全符合Java语法规范的脚本语言,并且又拥有自己的一些语法和方法,所以它和java是可以无缝衔接的,学了Java的一些基本语法后,就可以来在Jmeter中写写BeanShell脚本了 在利用jmeter进行接口测试或者性能测试的时候,…...

前端和后端 优化
1.前端资源优化 1.1 html结构优化 保证简洁、清晰的html结构,减少或避免多余的html标签 使用HTML5的web语义化标签,结构清晰且利于seo css文件在head中引入,js文件放在body底部引入,这样做可以防止阻塞。另外如果有需要提前加载的…...

C++编译与运行:其二、编译期和运行期的区别
C的编译分为四步,最终生成一个可执行文件。 C的运行,就是将可执行文件交给操作系统,按照机器码逐步执行,运行功能。 先看一个非常非常有趣的例子: class Father{ public:virtual void f(){cout<<"I am fat…...
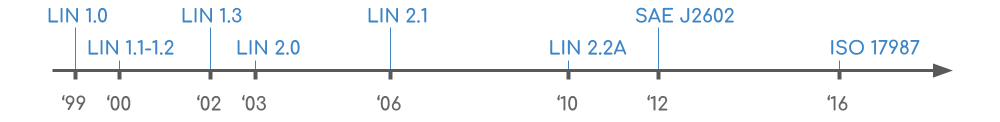
汽车电子专有名词与相应技术
1.EEA (Electronic & Electrical Architecture 电子电气架构) EEA在宏观上概括为物理架构与逻辑架构的结合,微观上通过众多电子元器件的协同配合,或集成式或分布式的系统级电子电气架构,具体详见专栏 新能源汽车电…...

idea 没加载 provided的包
目录 前言解决方案 前言 我的版本是IntelliJ IDEA 2022.1.4 (Community Edition),本地调试不知道为什么不加载provided的包。后来找到这篇文章https://youtrack.jetbrains.com/issue/IDEA-107048才知道这是个bug。不知道其他版本会不会出现这种问题。 解决方案 我…...

Hover:借贷新势力崛起,在经验与创新中找寻平衡
复苏中的Cosmos 如果让我选择一个最我感到可惜的区块链项目,我会选择Cosmos。 Cosmos最早提出并推动万链互联的概念,希望打通不同链之间的孤岛,彼时和另一个天王项目Polkadot号称跨链双雄。其跨链技术允许不同的区块链网络互相通信…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

Java中栈的多种实现类详解
Java中栈的多种实现类详解:Stack、LinkedList与ArrayDeque全方位对比 前言一、Stack类——Java最早的栈实现1.1 Stack类简介1.2 常用方法1.3 优缺点分析 二、LinkedList类——灵活的双端链表2.1 LinkedList类简介2.2 常用方法2.3 优缺点分析 三、ArrayDeque类——高…...

gorm 配置数据库
介绍 GORM 是 Go 语言中最流行的 ORM(对象关系映射)库之一,基于数据库操作的封装,提供类似 Django ORM / SQLAlchemy 的开发体验。 特性描述支持多种数据库MySQL、PostgreSQL、SQLite、SQL Server、ClickHouse 等自动迁移自动根…...
