【蓝桥集训】第七天并查集
作者:指针不指南吗
专栏:Acwing 蓝桥集训每日一题🐾或许会很慢,但是不可以停下来🐾
文章目录
- 1.亲戚
- 2.合并集合
- 3.连通块中点的数量
有关并查集的知识学习可以移步至—— 【算法】——并查集
1.亲戚
或许你并不知道,你的某个朋友是你的亲戚。
他可能是你的曾祖父的外公的女婿的外甥女的表姐的孙子。
如果能得到完整的家谱,判断两个人是否是亲戚应该是可行的,但如果两个人的最近公共祖先与他们相隔好几代,使得家谱十分庞大,那么检验亲戚关系实非人力所能及。
在这种情况下,最好的帮手就是计算机。
为了将问题简化,你将得到一些亲戚关系的信息,如Marry和Tom是亲戚,Tom和Ben是亲戚,等等。
从这些信息中,你可以推出Marry和Ben是亲戚。
请写一个程序,对于我们的关于亲戚关系的提问,以最快的速度给出答案。
输入格式
输入由两部分组成。
第一部分以 N,M开始。N 为问题涉及的人的个数。这些人的编号为 1,2,3,…,N。下面有 M 行,每行有两个数 ai,bia_i,b_iai,bi ,表示已知 aia_iai 和 bib_ibi 是亲戚。
第二部分以 Q 开始。以下 Q 行有 Q 个询问,每行为 ci,dic_i,d_ici,di ,表示询问 cic_ici 和 did_idi 是否为亲戚。
输出格式
对于每个询问ci,dic_i,d_ici,di ,输出一行:若 cic_ici 和 did_idi 为亲戚,则输出“Yes”,否则输出“No”。
数据范围
1≤N≤20000,
1≤M≤10610^6106 ,
1≤Q≤10610^6106 .输入样例:
10 7 2 4 5 7 1 3 8 9 1 2 5 6 2 3 3 3 4 7 10 8 9输出样例:
Yes No Yes
-
思路
- 把每个家族看成一个集合:人之间互为亲戚,则说明他们是一个家族的,用一个编号来表示;
- 这个题比较简单,就是并查集的两个朴素操作:
- 两个人互为亲戚,进行家族合并,即并查集合并
- 查询两个人是否为亲戚,即看看这两人的家族是否一样
-
代码实现
#include<bits/stdc++.h> using namespace std;const int N=200010;int n,m; //n表示人数,m表示操作的次数 int p[N];int find(int x) //找到家族编号,即根节点 {if(p[x]!=x) p[x]=find(p[x]);return p[x]; }int main() {scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) p[i]=i; //初始化父节点while(m--){ //m次合并操作,亲戚互认int a,b;scanf("%d%d",&a,&b);if(find(a)!=find(b)) p[find(a)]=find(b); //家族集合合并}int q;cin>>q;while(q--){ //q次查询,是否是亲戚,一个家族集合的int x,y;scanf("%d%d",&x,&y);if(find(x)==find(y)) puts("Yes"); else puts("No");}return 0; }
2.合并集合
一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。
现在要进行 m 个操作,操作共有两种:
M a b,将编号为 a 和 b 的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;Q a b,询问编号为 a 和 b 的两个数是否在同一个集合中;输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为
M a b或Q a b中的一种。输出格式
对于每个询问指令
Q a b,都要输出一个结果,如果 a 和 b 在同一集合内,则输出Yes,否则输出No。每个结果占一行。
数据范围
1≤n,m≤10510^5105
输入样例:
4 5 M 1 2 M 3 4 Q 1 2 Q 1 3 Q 3 4输出样例:
Yes No Yes
-
代码实现
#include<bits/stdc++.h> using namespace std;const int N=100010;int n,m; //n表示点的数量,m表示操作的次数 int p[N]; //存的每个节点的父节点int find(int x) //返回x的祖宗节点+路径压缩 {if(p[x]!=x) p[x]=find(p[x]);return p[x]; }int main() {scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) p[i]=i; //最开始,每个点都各自在一个集合中,so父节点就是他本身;while(m--){char op[2];int a,b;scanf("%s%d %d",op,&a,&b);//合并if(op[0]=='M') p[find(a)]=p[find(b)]; //让a的祖宗节点等于b的祖宗节点,让a的祖宗节点直接插在b祖宗节点下面else{if(find(a)==find(b)) puts("Yes"); //判断是否属于同一个集合else puts("No");} }return 0; }
注意
读入字母M或者是Q的时候,使用字符串op[2],是因为直接用char的话,可能会出现空格换行的问题作物,这种比较保险,记得在后面使用的时候,用op[0],不能直接使用op
puts自动包含换行
3.连通块中点的数量
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。
现在要进行 m 个操作,操作共有三种:
C a b,在点 a 和点 b 之间连一条边,a 和 b 可能相等;Q1 a b,询问点 a 和点 b 是否在同一个连通块中,a 和 b 可能相等;Q2 a,询问点 a 所在连通块中点的数量;输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为
C a b,Q1 a b或Q2 a中的一种。输出格式
对于每个询问指令
Q1 a b,如果 a 和 b 在同一个连通块中,则输出Yes,否则输出No。对于每个询问指令
Q2 a,输出一个整数表示点 a 所在连通块中点的数量每个结果占一行。
数据范围
1≤n,m≤10510^5105
输入样例:
5 5 C 1 2 Q1 1 2 Q2 1 C 2 5 Q2 5输出样例:
Yes 2 3
-
思路
-
连通块就是一个点的集合:集合中的点可以相互到达,直接或者是间接都是可以的;
-
这时候我们可以把它类比成一个树,运用并查集,一个点集合,我们可以用一个编号来表示,属于同一个编号,就说明两个点之间可以相互到达,在一个连通块里面;
-
有三个操作:
-
两点之间连一条边,那么这两个点所在集合中的点,都是可以相互到达的,即合成一个连通块,用并查集中的合并操作;
-
判断是否在一个连通块,用并查集的查询;
-
询问一个点集合的数量,需要我们额外维护,初始化的时候每个集合1个,合并的时候,两个集合数量相加,最后输出即可
-
-
-
代码实现
#include<bits/stdc++.h>using namespace std;const int N=1000010; int n,m; int p[N],sizel[N]; //p表示父节点,sizel表示集合的大小,记住sizel里面放的是祖宗节点,后面容易出错int find(int n) //返回祖宗节点 {if(p[n]!=n) p[n]=find(p[n]);return p[n]; }int main() {scanf("%d%d",&n,&m); //读入点的数量和操作的次数for(int i=1;i<=n;i++){ //初始化,父节点就是它本身;集合大小都是1,只有他自己p[i]=i;sizel[i]=1;}char op[5]; while(m--){scanf("%s",op); //读入操作的名字if(op[0]=='C'){ //合并int a,b;scanf("%d%d",&a,&b);if(find(a)==find(b)) continue; //相同则进入下个循环else{ //不同即操作,两步的顺序不能反!!!sizel[find(b)]+=sizel[find(a)]; //b的集合大小加上a的集合大小p[find(a)]=find(b); //让a的祖宗节点指向b的祖宗节点}}else if(op[1]=='1'){ //查询是否一个集合int a,b;scanf("%d%d",&a,&b);if(find(a)==find(b)) puts("Yes");else puts("No");}else{if(op[1]=='2') { //输出集合大小int d;scanf("%d",&d);printf("%d\n",sizel[find(d)]); }}}return 0; }

相关文章:

【蓝桥集训】第七天并查集
作者:指针不指南吗 专栏:Acwing 蓝桥集训每日一题 🐾或许会很慢,但是不可以停下来🐾 文章目录1.亲戚2.合并集合3.连通块中点的数量有关并查集的知识学习可以移步至—— 【算法】——并查集1.亲戚 或许你并不知道&#…...

【Playwright】扑面而来的Playwright测试框架
在当今快节奏的开发环境中,测试是软件开发的重要组成部分。 Microsoft Playwright 是一种流行的测试自动化框架,允许开发人员为 Web 应用程序编写端到端测试。 Playwright 建立在 Puppeteer 之上,这是另一个流行的测试自动化框架。在这篇博文…...
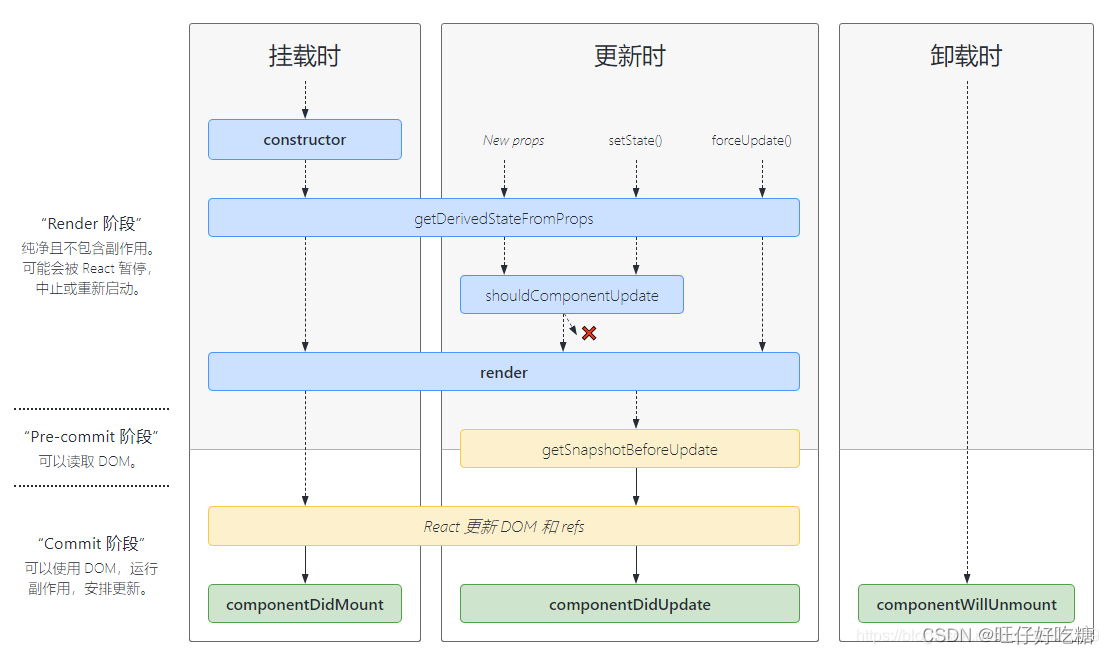
React(三) ——新、旧生命周期
🧁个人主页:个人主页 ✌支持我 :点赞👍收藏🌼关注🧡 文章目录⛳React生命周期🌋初始化阶段👣运行中阶段🏓销毁阶段🏫新生命周期的替代🚚react中性…...

IT男的一次中年破局尝试--出书
一、转战外企 接上回《人到中年——IT男择业感悟》后,自己从大央企去了某知名外企。外企虽然最近几年的日子已经没有10年前的辉煌与滋润,但相对来说,还能勉强找到工作与生活的平衡点。 划重点,35岁上下的人换工作理由…...

Python 内置函数eval()
Python 内置函数eval() eval(expression, globalsNone, localsNone) 函数用来执行一个字符串表达式,并返回表达式的值。 expression: 字符串表达式。global: 可选,globals必须是一个字典。locals: 可选,locals可以是任何映射对象。 示例 &…...

【ArcGIS Pro二次开发】系列学习笔记,持续更新,记得收藏
一、前言 这个系列是本人的一个学习笔记。 作为一个ArcGIS Pro二次开发的初学者,最困扰的就是无从入手。网上关于ArcGIS Pro二次开发的中文资料极少,官方文档对于我这样的英文苦手又太不友好。 在搜索无果后,决定自已动手,从头…...

EasyRecovery16MAC苹果版本Photo最新版数据恢复软件
无论是在工作学习中,还是在生活中,Word、Excle等办公软件都是大家很常用的。我们在使用电脑的过程中,有时会因自己的误删或电脑故障,从而导致我们所写的文档丢失了。出现这样的大家不要着急,今天小编就给大家推荐一款可…...

Go的string与strings.Builder
Go的string与strings.Builder 文章目录Go的string与strings.Builder一、strings.Builder 的优势二、string类型的值三、与string相比,Builder的优势体现在拼接方面3.1 Builder的拼接,与Builder的自动扩容3.2 手动扩容3.3 Builder 的重用四、strings.Buil…...

8.Spring Security 权限控制
1.简介入门JavaEE和SpringMVC :Spring Security就是通过11个Fliter进行组合管理小Demouser实体类user.type字段,0普通用户,1超级管理员,2版主补全get set tostringimplement UserDetails,重写以下方法// true: 账号未过…...

curl / python+selenium爬取网页信息
Python爬取网页信息 需求: 持续爬取某嵌入式设备配置网页上的状态信息 shell脚本 简单快速, 不用装插件只能爬取静态内容 用curl命令返回整个网页的内容用grep命令抓取其中某些字段结合正则表达式可多样查找但对于动态内容, 比如对某嵌入式设备配置网页上的一条不断更新的信…...

晶体塑性有限元 Abaqus 三维泰森多边形(voronoi模型)插件 V7.0
1 上一版本完整功能介绍: Voronoi晶体插件-6.0版本[新功能介绍] 晶体塑性有限元 Abaqus 三维泰森多边形(voronoi模型)插件 V6.0 2 新增功能模块 7.0版本新增功能模块包括:柱状晶体模块和分层晶体模块。 2.1 二维柱状晶体模块 …...

CPython解释器性能分析与优化
原文来自微信公众号“编程语言Lab”:CPython 解释器性能分析与优化 搜索关注 “编程语言Lab”公众号(HW-PLLab)获取更多技术内容! 欢迎加入 编程语言社区 SIG-元编程 参与交流讨论(加入方式:添加文末小助手…...
Linux 进程:理解进程和pcb
目录一、进程的概念二、CPU分时机制三、并发与并行1.并发2.并行四、pcb的概念一、进程的概念 什么是进程? 进程就是进行中的程序,即运行中的应用程序。比如:电脑上打开的LOL、QQ…… 这些都是一个个的进程。 什么是应用程序? 应用…...
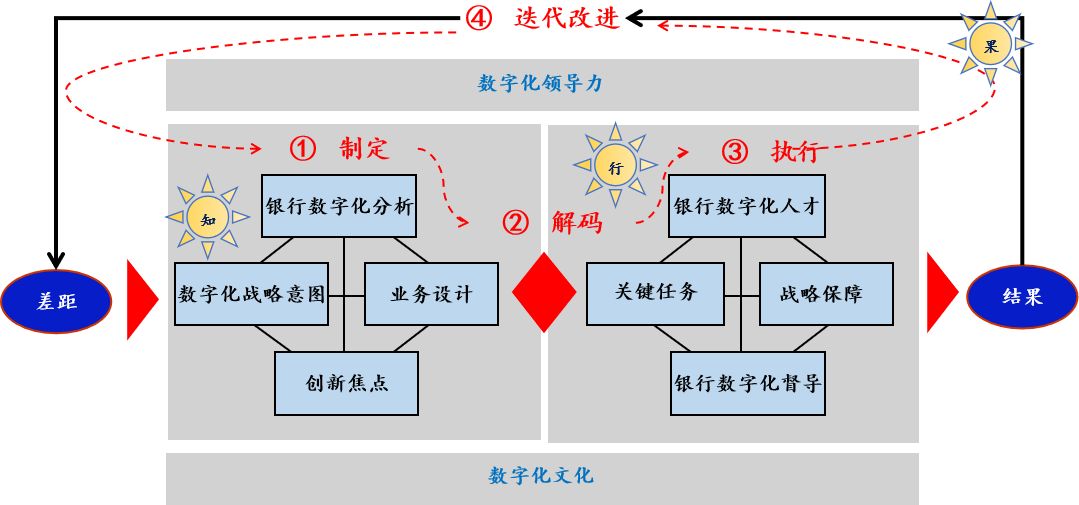
银行数字化转型导师坚鹏:招商银行数字化转型战略研究
招商银行数字化转型战略研究课程背景: 很多银行存在以下问题:不清楚如何制定银行数字化转型战略?不知道其它银行的数字化转型战略是如何演变的? 课程特色:用实战案例解读招商银行数字化转型战略。用独特视角解…...
java 一文讲透面向对象 (20万字博文)
目录 一、前言 二、面向对象程序设计介绍 1.oop三大特性 : 2.面向对象和面向过程的区别 : 3.面向对象思想特点 : 4.面向对象的程序开发 : 三、Java——类与对象 1.java中如何描述一个事物? 2.什么是类? 3.类的五大成员: 4.封装的前提——抽象 : 5.什么是对…...
使用file-selector-button美化原生文件上传
前言 你平时见到的上传文件是下面这样的? 还是下面这种美化过的button样式 还是下面这种复杂的上传组件。 <input type="file" >:只要指定的是type类型的input,打开浏览器就是上面第一种原生的浏览器默认的很丑的样式。 下面的两种是我从ElementUI截的图,…...

0402换元积分法-不定积分
文章目录1 第一类换元法1.1 定理11.2 例题1.2 常见凑微分形式1.2.1常见基本的导数公式的逆运算1.2.2被积函数含有三角函数2 第二类换元法2.1 定理22.2 常见第二换元代换方法2.2.1 三角代换-弦代换2.2.2 三角代换-切代换2.2.3 三角代换-割代换2.2.4 三角代换汇总2.2.5 倒代换2.2…...
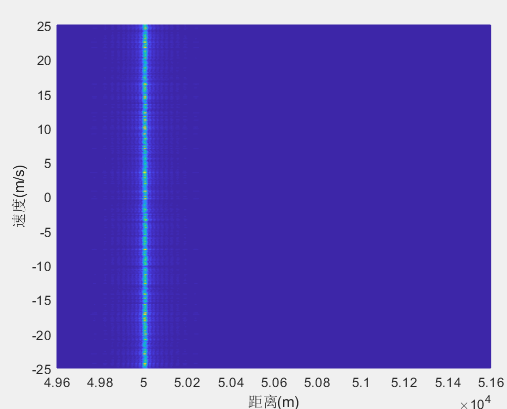
信号类型(雷达)——脉冲雷达(三)
系列文章目录 《信号类型(雷达通信)》 《信号类型(雷达)——雷达波形认识(一)》 《信号类型(雷达)——连续波雷达(二)》 文章目录 前言 一、相参雷达 1…...
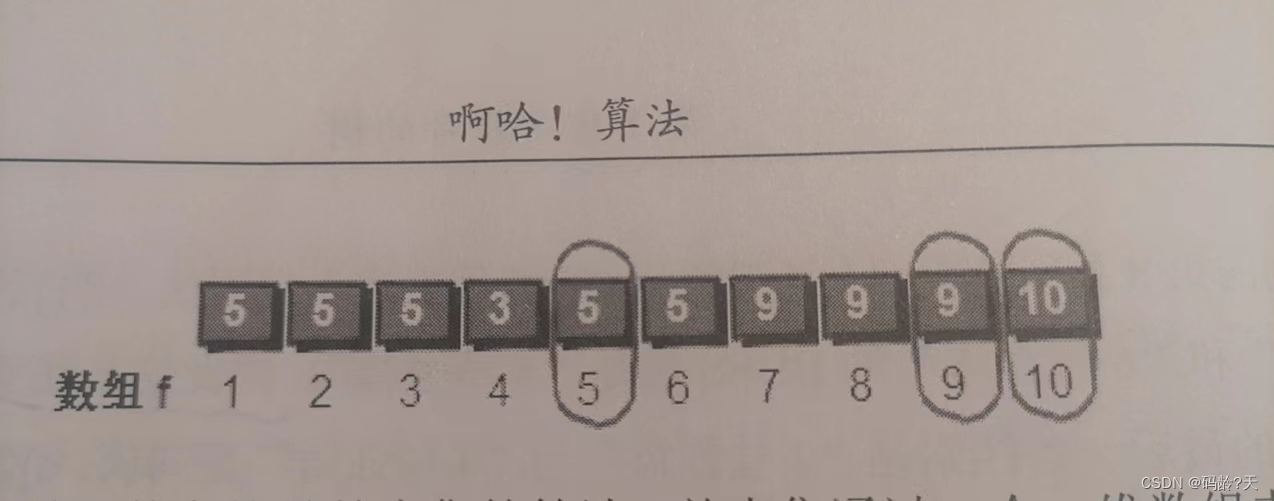
并查集(13张图解)--擒贼先擒王
目录 前言 故事 🌼思路 🌼总结 🌼代码 👊观察过程代码 👊正确代码 👊细节代码 来自《啊哈算法》 前言 刚学了树在优先队列中的应用--堆的实现 那么树还有哪些神奇的用法呢?我们从一…...
Flutter3引用原生播放器-IOS(Swift)篇
前言由于Flutter项目中需要使用到播放器功能,因此对flutter中各种播放器解决方案进行了一番研究和比对,最后决定还是自己通过Plugin的方法去引用原生播放器符合自己的需求,本篇文章会对各种解决方案做一个简单的比较,以及讲解一下…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...
