NOIP2023模拟6联测27 C. 点餐
NOIP2023模拟6联测27 C. 点餐
题目大意
有 n n n 种菜品,每样菜品有 a i , b i a_i , b_i ai,bi
假设有某位顾客点了 k k k 样菜品,那么价格为 ∑ i = 1 k a p i + max i = 1 k b p i \sum_{i = 1}^k a_{p_i}+\max_{i = 1}^kb_{p_i} ∑i=1kapi+maxi=1kbpi
询问所有的 k ∈ ( 1 , n ) k \in(1 , n) k∈(1,n) 的答案。
思路
先把输入按 b b b 排序
设 w ( k , x ) w(k ,x) w(k,x) 为要选在前 x x x 里面选 k k k 个,那么
就是前 x x x 个菜品内最小的 k − 1 k - 1 k−1 个 a a a 加上 a x + b x a_x +b_x ax+bx
显然,决策满足单调性,所以可以用一个分治来搞
维护最小的前 k − 1 k - 1 k−1 个 a a a 可以用主席树
code
#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
#define LL long long
using namespace std;
const int N = 2e5 + 5;
const LL inf = 1e18 + 5;
int n , pos , rt[N] , m , ans1[N];
LL ans[N] , a[N];
struct Re {LL a , b;
} re[N << 1];
struct Tr {int lp , rp , cnt;LL val;
} tr[10000005];
bool cmp1 (Re x , Re y) { return x.a < y.a; }
bool cmp2 (Re x , Re y) { return x.b < y.b; }
void glp (int p) {if (!tr[p].lp) tr[p].lp = ++pos;
}
void grp (int p) {if (!tr[p].rp) tr[p].rp = ++pos;
}
void change (int lst , int p , int l , int r , int x) {if (l == r) {tr[p].cnt ++;tr[p].val += a[l];}else {int mid = l + r >> 1;if (x <= mid) {glp (p);tr[p].rp = tr[lst].rp;change (tr[lst].lp , tr[p].lp , l , mid , x);}else {grp (p);tr[p].lp = tr[lst].lp;change (tr[lst].rp , tr[p].rp , mid + 1 , r , x);}tr[p].val = tr[tr[p].lp].val + tr[tr[p].rp].val;tr[p].cnt = tr[tr[p].lp].cnt + tr[tr[p].rp].cnt;}
}
LL getsum (int p , int l , int r , int k) {if (l == r)return a[l];else {int mid = l + r >> 1;if (tr[tr[p].lp].cnt >= k) {return getsum (tr[p].lp , l , mid , k);}else {return getsum (tr[p].rp , mid + 1 , r , k - tr[tr[p].lp].cnt) + tr[tr[p].lp].val;}}
}
void solve (int l , int r , int L , int R) {if (l > r) return;int mid = l + r >> 1 , now1= 0;LL now;fu (i , max (L , mid) , R) {// now = re[i].b + re[i].a + getsum (rt[i - 1] , 1 , n , mid - 1);now = re[i].b + getsum (rt[i] , 1 , n , mid);if (ans[mid] > now) {ans[mid] = now;now1 = i;ans1[mid] = i;}}solve (l , mid - 1 , L , now1);solve (mid + 1 , r , now1 , R);
}
int main () {freopen ("order.in" , "r" , stdin);freopen ("order.out" ,"w" , stdout);scanf ("%d" , &n);fu (i , 1 , n)scanf ("%lld%lld" , &re[i].a , &re[i].b);sort (re + 1 , re + n + 1 , cmp1);fu (i , 1 , n) a[i] = re[i].a , re[i].a = i;sort (re + 1 , re + n + 1 , cmp2);fu (i , 1 , n) ans[i] = inf;fu (i , 0 , n) rt[i] = ++pos;fu (i , 1 , n) {change (rt[i - 1] , rt[i] , 1 , n , re[i].a);}solve (1 , n , 1 , n);fu (i , 1 , n) {printf ("%lld\n" , ans[i]);}return 0;
}
相关文章:

NOIP2023模拟6联测27 C. 点餐
NOIP2023模拟6联测27 C. 点餐 题目大意 有 n n n 种菜品,每样菜品有 a i , b i a_i , b_i ai,bi 假设有某位顾客点了 k k k 样菜品,那么价格为 ∑ i 1 k a p i max i 1 k b p i \sum_{i 1}^k a_{p_i}\max_{i 1}^kb_{p_i} ∑i1kapi…...

简单聊聊远程协同运维定义以及优势-行云管家
很多新人小伙伴对于远程协同运维不是很了解,今天我们就来简单聊聊远程协同运维定义以及优势。 远程协同运维定义 远程协同运维其实非常容易理解,主要是指计算机系统技术服务工程相关的人员通过局域网或者是其他网络对于它来进行连接,共同远…...

Ortec974A EPICS IOC程序
Ortec974A设备介绍,请见Ortec -- 974A 四通道100-MHz计时器/计数器_ortec974a_EPICS Technical的博客-CSDN博客 1) 创建一个用户存放这个IOC程序结构的目录: rootorangepi4-lts:/usr/local/EPICS/program# mkdir ortec974A rootorangepi4-l…...

JS-文件下载,实现在ios也是下载 而不是预览,
需求 通过A链接的方式,把从后台获取到的文件下载到本地,实现在移动端,PC端都能下载 问题 通过ajax请求后端生成的文件流之后,创建BLOB文件进行下载,在PC端和移动安卓端都可以实现下载到本地和对应的手机,而在IOS端的…...

Leetcode.275 H 指数 II
题目链接 Leetcode.275 H 指数 II mid 题目描述 给你一个整数数组 c i t a t i o n s citations citations ,其中 c i t a t i o n s [ i ] citations[i] citations[i] 表示研究者的第 i i i 篇论文被引用的次数, c i t a t i o n s citations citat…...

代码随想录Day40-单调栈:力扣第496e、503m、42h、84h题
496e. 下一个更大元素 I 题目链接 代码随想录文章讲解链接 方法一:单调栈哈希表 用时:13m52s 思路 维护一个栈底到栈顶是单调递减的栈,从后往前遍历数组nums2,更新栈。nums2当前元素nums2[i]的下一个更大元素就是栈顶元素&am…...
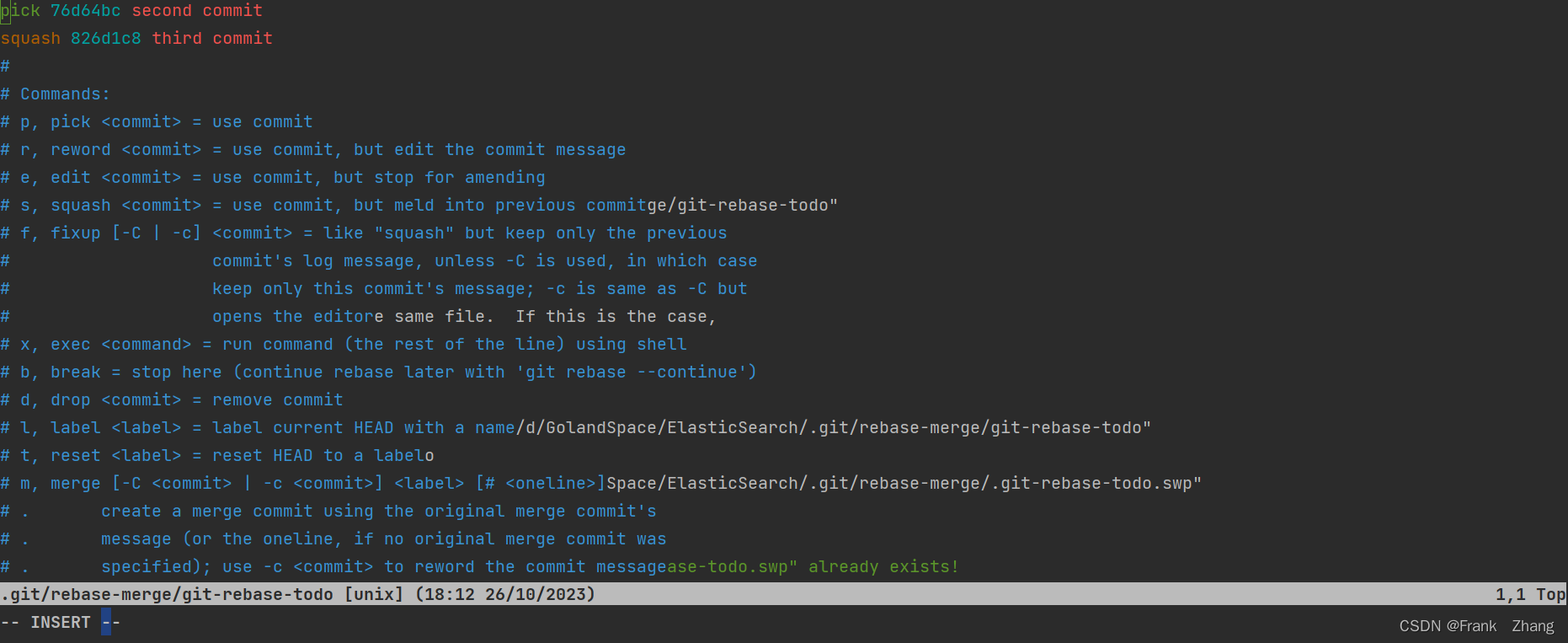
Git窗口打开vim后如何退出编辑(IDEA/Goland等编辑器)
最近在学习git高级操作过程中,遇到了一下问题: 我在学习Git合并多个commit为一个的时候,需要输入一个命令 git rebase -i HEAD~2 这说明已经是编辑模式了。当我写好后,我还按照原来在linux上的按下ESC键,但是只是光…...

【CSDN 每日一练 ★★☆】【二叉树/BSF】二叉树的层序遍历
【CSDN 每日一练 ★★☆】【二叉树/BSF】二叉树的层序遍历 二叉树 BSF 题目 给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。 示例: 二叉树:[3,9,20,null,nul…...
Golang | Zinx学习笔记(一)
参考 http://zinx.me/ https://www.kancloud.cn/aceld/zinx/1960213 https://www.yuque.com/aceld/tsgooa/gx01meg5ow4pftac 说明 zinx是一个基于Golang的轻量级并发服务器框架。 目前zinx已经在很多企业进行开发使用,具体使用领域包括:后端模块的消息中转、长链…...

【Java 进阶篇】在Java Web应用中获取ServletContext对象详解
在Java Web应用开发中,ServletContext对象扮演着重要的角色,它允许你在整个Web应用程序中存储和共享数据。ServletContext对象是Servlet容器提供的一种用于管理Web应用程序的全局信息的方式。本文将详细探讨ServletContext对象的概念、用途以及如何在Jav…...

负债6W,依靠这个项目副业6个月还清欠款,还多存了10W+
真不敢想象负债6W“走投无路”的我还能通过副业逆天翻盘,6个月还清欠款,还让我多了10W存款,现在小日子也是相当滋润,吃穿不愁,不用过多为生计而奔波操劳。 仅代表个人收益 网盘下载地址:【安卓软件】音魔变…...
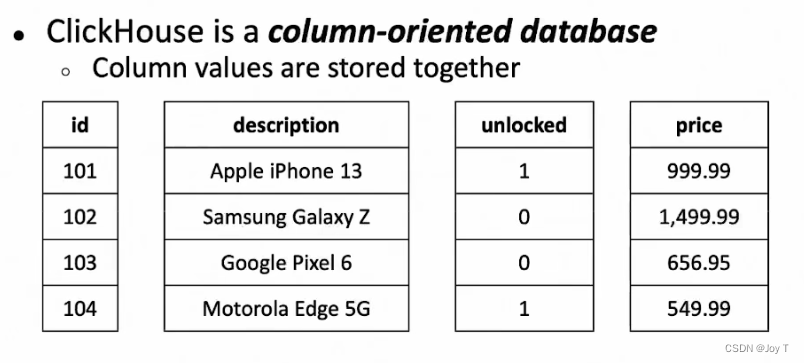
快速了解ClickHouse!
简介 ClickHouse是一个开源列式数据库管理系统(DBMS),用于在线分析处理(OLAP): 列式存储:与传统的行式数据库不同,ClickHouse以列的形式存储数据,这使得在分析大量数据时…...
PythonWEB
文章目录 前端简介1. 什么是网页2. 网页的组成3. 网页的优势4. 前端三剑客5. 编写步骤6. HTTP协议 HTML51. HTML介绍2. 元素3. 使用4. 基本结构解析5. 常用标签文本标签容器标签列表标签表格标签表单标签 对于文件数据的提交需要满足以下两个条件:6. 标签分类 前端简…...
【工具问题】IDEA每次关闭的时候都会弹框显示closing project,然后弹框持续很久就像卡住了
idea关闭的时候出现问题 问题展示为什么会出现这种情况怎么解决 问题展示 我idea已经关闭了,但是这个弹框要持续很久才能关闭 为什么会出现这种情况 我的plugins原本是加载不出来的,所以我按照网上说法去做 怎么解决 file->setting,再如图选择…...

从瀑布模式到水母模式:ChatGPT如何赋能软件研发全流程
文章目录 前言内容简介作者简介专家推荐读者对象直播预告 前言 计算机技术的发展和互联网的普及,使信息处理和传输变得更加高效,极大地改变了金融、商业、教育、娱乐等领域的运作方式。数据分析、人工智能和云计算等新兴技术,也在不断地影响和…...
类变量/方法、main语法、代码块
一.类变量和方法 思维导图概览: 1.1类变量(静态变量) 1.什么叫做类变量/方法? ——给类中的成员属性或成员方法加上static关键字进行修饰,类变量/方法也叫做静态变量/方法,静态变量/方法被类的自身所有对…...

[SHCTF 校外赛道] crypto
终于都结束了,这些新生赛太漫长了。不过这个也还是有些难度的,好多整不来。抓紧时间整理一下。 week1 第1周基本是古典密码,古典和现代最大的区别是古典全靠猜,现在都是数学 立正 wl hgrfhg 4gNUx4NgQgEUb4NC64NHxZLg636V6CDBi…...
vue3从基础到入门(一)
文章目录 简介提升使用创建脚手架vite 常用Composition APIsetuprefreactive函数响应式vue2响应式vue3实现响应式 reactive对比ref注意计算属性computed函数 监视watch函数watchEffect函数 生命周期hook函数toRef 简介 2020年9月18日,Vue.js发布3.0版本,…...

枚举类型 表示不同的 HTTP 状态码和相应的错误消息
java web业务中经常用常量来表示不同的 HTTP 响应状态,比如 public enum AppHttpCodeEnum {// 成功段0SUCCESS(200,"操作成功"),// 登录段1~50NEED_LOGIN(1,"需要登录后操作"),LOGIN_PASSWORD_ERROR(2,"密码错误"),// TOKEN50~100TOKEN_INVALID…...
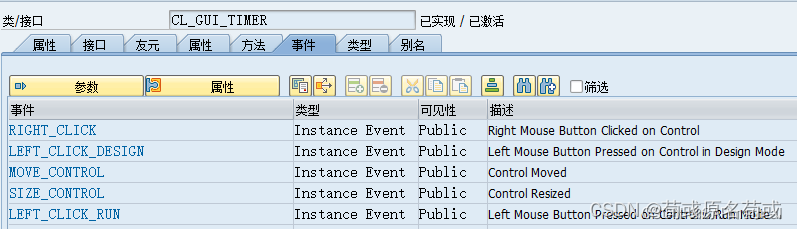
SAP 使用cl_gui_timer自动刷新屏幕的用法详解 <转载>
原文链接:https://blog.csdn.net/SAPmatinal/article/details/130483382 SAP 使用cl_gui_timer自动刷新屏幕的用法详解 这个类在初始化的时候会设置一个定时间隔,每隔这个时间就会触发一次FINISHED事件。利用这个类的特性,可以实现很多东西&…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...
