基于适应度相关算法的无人机航迹规划-附代码
基于适应度相关算法的无人机航迹规划
文章目录
- 基于适应度相关算法的无人机航迹规划
- 1.适应度相关搜索算法
- 2.无人机飞行环境建模
- 3.无人机航迹规划建模
- 4.实验结果
- 4.1地图创建
- 4.2 航迹规划
- 5.参考文献
- 6.Matlab代码
摘要:本文主要介绍利用适应度相关算法来优化无人机航迹规划。
1.适应度相关搜索算法
适应度相关算法原理请参考:https://blog.csdn.net/u011835903/article/details/119946003
2.无人机飞行环境建模
? 环境模型的建立是考验无人机是否可以圆满完成人类所赋予各项任务的基
础和前提,其中第一步便是如何描述规划空间中的障碍物。首先我们将采取函数模拟法模拟地貌特征。其函数表达式为:
z ( x , y ) = s i n ( y + a ) + b s i n ( x ) + c c o s ( d y 2 + x 2 ) + e c o s ( y ) + f s i n ( f y 2 + x 2 ) + g c o s ( y ) (1) z(x,y)=sin(y+a)+bsin(x)+ccos(d\sqrt{y^2+x^2})+ecos(y)+fsin(f\sqrt{y^2+x^2})+gcos(y)\tag{1} z(x,y)=sin(y+a)+bsin(x)+ccos(dy2+x2)+ecos(y)+fsin(fy2+x2)+gcos(y)(1)
其中, ( x , y ) (x, y) (x,y) 为地形上某点投影在水平面上的点坐标, z z z 则为对应点坐标的高度。式中 a , b , c , d , e , f , g a, b, c, d, e, f , g a,b,c,d,e,f,g 是常系数,想要得到不同的地貌特征可以通过改变其常系数的大小,以上建模是作为环境模型的基准地形信息。但为了得到障碍区域我们还需要在这个基准地形上叠加山峰模型,这样就可以模拟像山峰、丘陵等障碍地理信息。山峰模型的数学表达式为:
h ( x , y ) = ∑ i h i e x p [ − ( x − x o i ) 2 a i 2 − ( y − y o i ) 2 b i 2 ] + h o (2) h(x,y)=\sum_ih_iexp[-\frac{(x-x_{oi})^2}{a_i^2}-\frac{(y-y_{oi})^2}{b_i^2}]+h_o \tag{2} h(x,y)=i∑hiexp[−ai2(x−xoi)2−bi2(y−yoi)2]+ho(2)
式 (2)中, h o h_o ho 和 h i h_i hi 分别表示基准地形和第 i i i座山峰的高度, ( x o i , y o i ) (xoi , y oi ) (xoi,yoi)则表示第 i座山峰的中心坐标位置,a i 和 b i 分别是第 i 座山峰沿 x 轴和 y 轴方向的坡度。由式(1)和(2),我们可以得到如下表达式:
Z ( x , y ) = m a x [ z ( x , y ) , h ( x , y ) ] (3) Z(x,y)=max[z(x,y),h(x,y)]\tag{3} Z(x,y)=max[z(x,y),h(x,y)](3)
无人机在躲避障碍物的同时也会经常遇到具有威胁飞行安全的区域,我们称之为威胁区域。这些威胁区域可以是敌人的雷达和防空导弹系统的探测威胁区域也可以是一些其它的威胁,一旦无人机进入这些区域很有可能会被击落或者坠毁。为了简化模型,本文采用半径为 r 的圆柱形区域表示威胁区域,其半径的大小决定威胁区域的覆盖范围。每一个圆柱体的中心位置是对无人机构成最大威胁的地方并向外依次减弱。
3.无人机航迹规划建模
? 在环境建模的基础上,无人机航迹规划需要考虑到在执行复杂任务的过程中自身性能约束要求,合理的设计航迹评价函数才能使得适应度相关搜索算法得出的最后结果符合要求,并保证规划出的航迹是有效的。考虑到实际环境中,无人机需要不断适应变化的环境。所以在无人机路径规划过程中,最优路径会显得比较复杂,并包含许多不同的特征。基于实际的情况,本文采用较为复杂的航迹评价函数进行无人机路径规划。影响无人机性能的指标主要包括航迹长度、飞行高度、最小步长、转角代价、最大爬升角等。
? 搜索最佳路径通常与搜索最短路径是密不可分的。在无人机航迹规划过程中,航迹的长度对于大多数航迹规划任务来说也是非常重要的。众所周知,较短的路线可以节省更多的燃料和更多的时间并且发现未知威胁的几率会更低。我们一般把路径定义为无人机从起始点到终点所飞行路程的值,设一条完整的航线有 n n n个节点,其中第 i i i个航路点和第 i + 1 i+1 i+1个航路点之间的距离表示为 l i l_i li ,这两个航路点的坐标分别表示为 ( x i , y i , z i ) (x_i,y_i,z_i ) (xi,yi,zi), ( x i + 1 , y i + 1 , z i + 1 ) (x_{i+1}, y_{i+1},z_{i+1}) (xi+1,yi+1,zi+1)并分别记作 g ( i ) g(i) g(i)和 g ( i + 1 ) g(i+1) g(i+1)。航迹需要满足如下条件:
{ l i = ∣ ∣ g ( i + 1 ) − g ( i ) ∣ ∣ 2 L p a t h = ∑ i = 1 n − 1 l i (4) \begin{cases} l_i = ||g(i+1)-g(i)||_2\\ L_{path}=\sum_{i=1}^{n-1}l_i \end{cases}\tag{4} {li=∣∣g(i+1)−g(i)∣∣2Lpath=∑i=1n−1li(4)
在飞行的过程中会遇到障碍物或者进入威胁区域,如果无人机无法躲避障碍物或者飞入了威胁区域将面临被击落或坠毁的危险以至于无法到达终点,记为 L p a t h = ∞ L_{path}=\infty Lpath=∞,但是无穷函数在实际问题中很难表示,我们采用惩罚的方式进行处理。一般情况下,为了利用地形覆盖自身位置,无人机应尽可能降低高度这可以帮助自身避免一些未知雷达等威胁。但是太低的飞行高度同样会加大无人机同山体和地面的撞击几率,因此设定稳定的飞行高度是非常重要的。飞行高度不应该有太大的变化,稳定的飞行高度可以减少控制系统的负担,节省更多的燃料 。为了使无人机飞行更加安全,给出的飞行高度模型:
{ h h e i g h t = 1 n ∑ i = 0 n − 1 ( z ( i ) − z ‾ ) 2 z ‾ = 1 n ∑ i = 0 n − 1 z ( i ) (5) \begin{cases} h_{height}=\sqrt{\frac{1}{n}\sum_{i=0}^{n-1}(z(i)-\overline{z})^2}\\ \overline{z}=\frac{1}{n}\sum_{i=0}^{n-1}z(i) \end{cases}\tag{5} {hheight=n1∑i=0n−1(z(i)−z)2z=n1∑i=0n−1z(i)(5)
无人机的可操作性也受到其转角代价函数的限制。,在飞行过程中无人机的转角应不大于其预先设定的最大转角,转角的大小会影响其飞行的稳定性。本文的研究中,设定最大转角为 Φ Φ Φ,当前转角为 θ \theta θ并且 a i a_i ai是第 i i i段航路段向量。
{ c o s θ = a i T a i + 1 ∣ a i ∣ ∣ a i + 1 ∣ J t u r n = ∑ i = 1 n ( c o s ( Φ − c o s θ ) ) (6) \begin{cases} cos\theta =\frac{a_i^Ta_{i+1}}{|a_i||a_{i+1}|}\\ J_{turn}=\sum_{i=1}^n(cos(\Phi-cos\theta)) \end{cases}\tag{6} {cosθ=∣ai∣∣ai+1∣aiTai+1Jturn=∑i=1n(cos(Φ−cosθ))(6)
其中, ∣ a ∣ |a| ∣a∣代表矢量 a a a的长度。
? 通过对以上三个方面建立了无人机航迹规划的代价函数,可以得出本文的航迹评价函数如下:
J c o s t = w 1 L p a t h + w 2 h h e i g h t + w 3 J t u r n (7) J_{cost}=w_1L_{path}+w_2h_{height}+w_3J_{turn} \tag{7} Jcost=w1Lpath+w2hheight+w3Jturn(7)
其中, J c o s t J_{cost} Jcost是总的代价函数,参数 w i w_i wi , i = 1 , 2 , 3 i=1,2,3 i=1,2,3 表示每个代价函数的权值,且满足如下条件:
{ w i ≥ 0 ∑ i = 1 3 w i = 1 (8) \begin{cases} w_i\geq0 \\ \sum_{i=1}^3 w_i=1 \end{cases} \tag{8} {wi≥0∑i=13wi=1(8)
通过对总的代价函数进行有效地处理,我们可以得到由线段组成的航迹。不可否认的是得到的路径往往是仅在理论上可行,但为了实际可飞,有必要对航迹进行平滑处理。本文采用三次样条插值的方法对路径进行平滑。
4.实验结果
4.1地图创建
设置地图参数a, b, c, d, e, f , g=1。地图大小为:200*200。设置三个山峰,山峰信息如表1所示。威胁区域信息如表2所示
| 信息 | 山峰中心坐标 | 山峰高度 | 山峰X方向坡度 | 山峰y方向坡度 |
|---|---|---|---|---|
| 山峰1 | [60,60] | 50 | 20 | 20 |
| 山峰2 | [100,100] | 60 | 30 | 30 |
| 山峰3 | [150,150] | 80 | 20 | 20 |
| 信息 | 威胁区域中心坐标 | 威胁区域半径 |
|---|---|---|
| 威胁区域1 | [150,50] | 30 |
| 威胁区域2 | [50,150] | 20 |
创建的地图如下:

4.2 航迹规划
设置起点坐标为[0,0,20],终点坐标为[200,200,20]。利用适应度相关算法对航迹评价函数式(7)进行优化。优化结果如下:
在这里插入图片描述

从结果来看,适应度相关算法规划出了一条比较好的路径,表明算法具有一定的优势。
5.参考文献
[1]薛建凯. 一种新型的群智能优化技术的研究与应用[D].东华大学,2020.DOI:10.27012/d.cnki.gdhuu.2020.000178.
6.Matlab代码
相关文章:

基于适应度相关算法的无人机航迹规划-附代码
基于适应度相关算法的无人机航迹规划 文章目录 基于适应度相关算法的无人机航迹规划1.适应度相关搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用适应度相关算法来优化无人机航迹…...
jmeter BeanShell预处理程序:报错Error invoking bsh method: eval...
1、jmeter运行报错: ERROR o.a.j.u.BeanShellInterpreter: Error invoking bsh method: eval In file: inline evaluation of: " . . . Encountered "" at line 13, column 23. WARN o.a.j.m.BeanShellPreProcessor: Problem in BeanShell scri…...

使用springboot对Elasticsearch 进行索引的增、删、改、查
一 SpringBoot Elasticsearch 项目环境搭建 1.1 修改pom文件添加依赖 目前使用spring-boot-starter-parent版本为2.2.8.RELEASE 对应spring-data-elasticsearch版本为2.2.8.RELEASE,版本对应可以自行百度,如果不行直接用elasticsearch-rest-high-lev…...

Project#2: Extendible Hash Index
文章目录 准备Task #1-Read/Write Page GuardsBasicPageGuard/ReadPageGuard/WritePageGuardUpgradeWrappersTests Task #2-Extendible Hash Table PagesHash Table Header Pages**成员变量:****方法实现:** Hash Table Directory Pages**成员变量&#…...
Emscripten + CMakeLists.txt 将 C++ 项目编译成 WebAssembly(.wasm)/js,并编译 Html 测试
背景:Web 端需要使用已有的 C 库(使用 CMake 编译),需要将 C 项目编译成 WebAssembly(.wasm) 供 js 调用。 上篇文章《Mac 上安装 Emscripten》 已讲解如何安装配置 Emscripten 环境。 本篇文章主要讲解如何将基于 CMakeLists 配…...
MATLAB中preparets函数用法
目录 语法 说明 示例 准备开环和闭环网络的数据 preparets函数的功能是为网络模拟或训练准备输入和目标时间序列数据 语法 [Xs,Xi,Ai,Ts,EWs,shift] preparets(net,Xnf,Tnf,Tf,EW) 说明 [Xs, Xi, Ai, Ts, EWs, shift] preparets(net, Xnf, Tnf, Tf, EW) 这个函数接受…...
ARM 版 OpenEuler 22.03 部署 KubeSphere v3.4.0 不完全指南续篇
作者:运维有术 前言 知识点 定级:入门级KubeKey 安装部署 ARM 版 KubeSphere 和 KubernetesARM 版 KubeSphere 和 Kubernetes 常见问题 实战服务器配置 (个人云上测试服务器) 主机名IPCPU内存系统盘数据盘用途ks-master-1172.16.33.1661650200KubeSp…...

react官网
应急方案 – React 中文文档 (docschina.org) 正版卡死版 Hooks FAQ – React (reactjs.org) 英文流畅版 应急方案 – React 中文网 (nodejs.cn) 盗版流畅版(翻译有稍稍的问题) http://www.react-cn.com/index.html 黄版...
前端css介绍
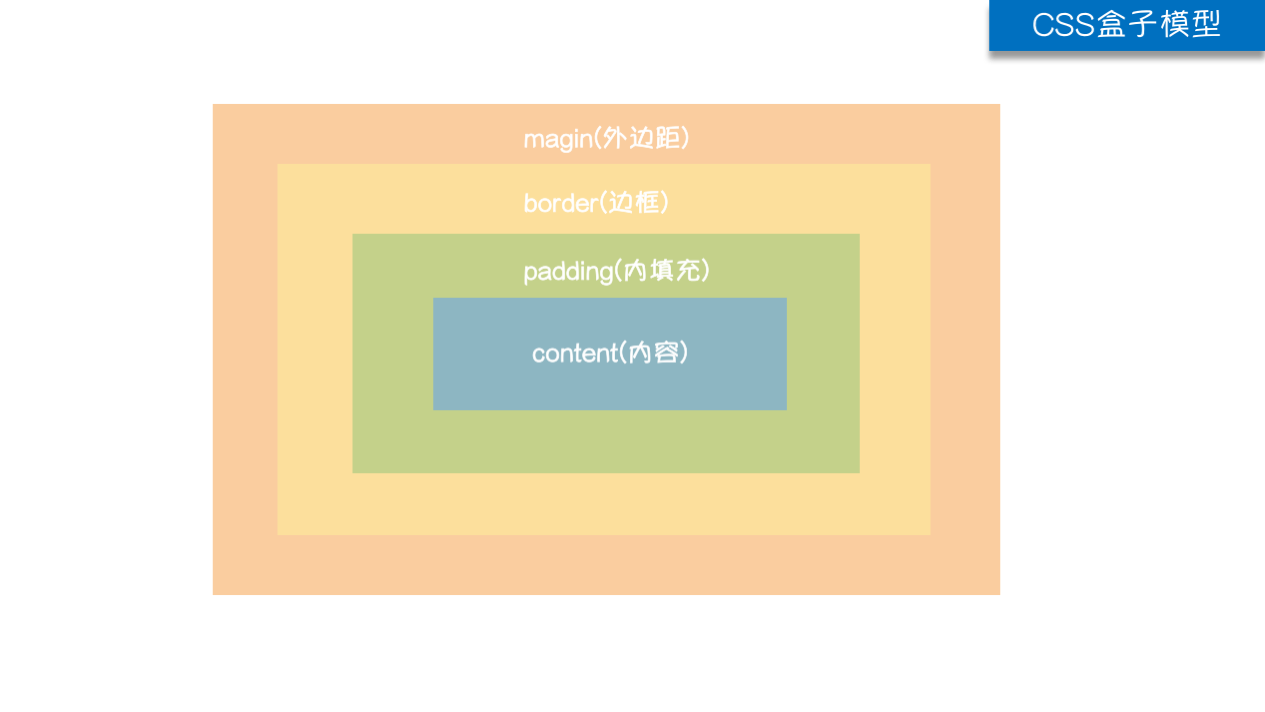
CSS介绍 CSS(Cascading Style Sheet,层叠样式表)定义如何显示HTML元素。 当浏览器读到一个样式表,它就会按照这个样式表来对文档进行格式化(渲染)。 CSS语法 CSS实例 每个CSS样式由两个组成部分:选择器和…...

MySql创建索引
在MySQL中,可以使用CREATE INDEX语句来创建索引。以下是创建索引的基本语法: CREATE INDEX index_name ON table_name (column1, column2, ...);其中,index_name是索引的名称,可以自定义(也可以不指定索引名称&#x…...

前后端分离vue+springboot家庭理财账单财务管理系统
项目介绍: 该系统能够管理家庭收入支出,并且能直观得表现收支状态。主要功能包括用户管理、收支管理、财务管理、统计收支情况等功能。 技术栈: 后端: SpringBoot,Sa-Token,MyBatis-Plus,MyB…...
LeetCode:2003. 每棵子树内缺失的最小基因值(C++)
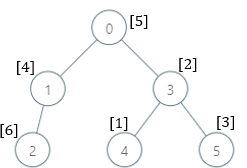
目录 2003. 每棵子树内缺失的最小基因值 题目描述: 实现代码与解析: dfs 启发式合并 原理思路: 2003. 每棵子树内缺失的最小基因值 题目描述: 有一棵根节点为 0 的 家族树 ,总共包含 n 个节点,节点编…...

React Hooks之useContext使用
官方文档写道:在组件的顶层调用 useContext 来读取和订阅 context。 我理解就是一个“全局变量”的概念。它可以用来声明一个变量,然后在各个组件中使用,避免了props一级一级往下传,当然使用场景有限,比如设置一个主题…...
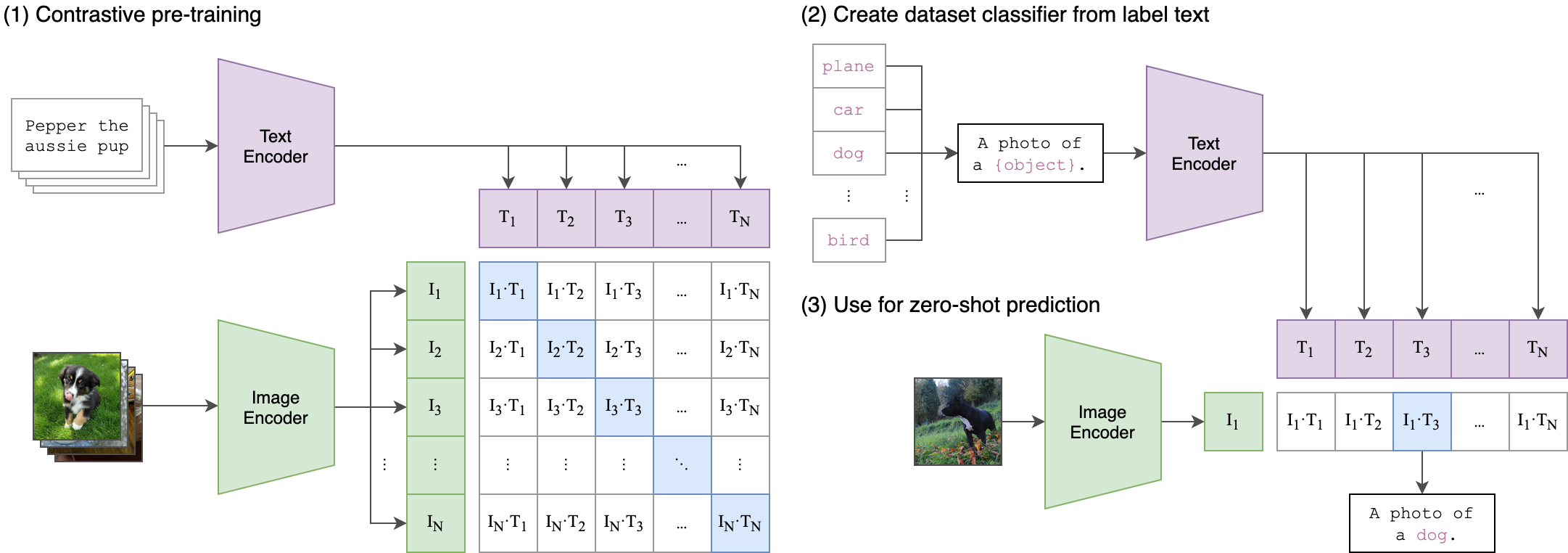
多模态对比语言图像预训练CLIP:打破语言与视觉的界限
项目设计集合(人工智能方向):助力新人快速实战掌握技能、自主完成项目设计升级,提升自身的硬实力(不仅限NLP、知识图谱、计算机视觉等领域):汇总有意义的项目设计集合,助力新人快速实…...

使用s3cmd访问S3存储 -【真实案例】
背景 项目中使用到了 S3 存储(基于华为云 OBS),并且在应用服务器上开通了到 S3 存储的防火墙。 👉 目标:在应用服务器上验证 S3 存储是否通畅可用。 👉 选型:经过分析,发现在 Linux 下可以使用 s3cmd 来访问 S3 存储。 s3cmd 简介 s3cmd 是一个开源免费的、基于 P…...
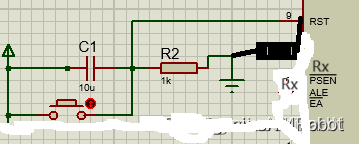
51单片机复位电容计算与分析(附带Proteus电路图)
因为iC x (dU/dt).在上电瞬间,U从0变化到U,所以这一瞬间就是通的,然后这就是一个直流回路,因为电容C直流中是断路的,所以就不通了。 然后来分析一下这个电容的电压到底是能不能达到单片机需要的复位电压。 这是一个线性电容&…...

前端性能瓶颈崩溃项目?Webpack助力解决!
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 📝 个人网站 :《 江城开朗的豌豆🫛 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 ⭐ 专栏简介 📘 文章引言 一、背…...

纷享销客BI,助力企业激活数据价值,科学企业决策
10月25日上午,国家数据局正式挂牌成立,这标志着我国数字经济发展将进入新的发展阶段,也将有力促进数据要素技术创新、开发利用和有效治理,以数据强国支撑数字中国的建设。伴随数据作为企业新的生产要素的意义不断凸显,…...
SpringBoot整合阿里云OSS对象存储
文章目录 1、OSS介绍及开通1.1、阿里云OSS简介1.2、开通OSS 2、创建存储空间bucket及密钥获取2.1、创建存储空间2.2、获取密钥 3、OSS快速入门案例4、在springboot项目中整合4.1、将oss配置放到yml文件中4.2、创建Oss属性类,接收yml文件中的属性4.3、封装文件上传功…...
【ES专题】ElasticSearch快速入门
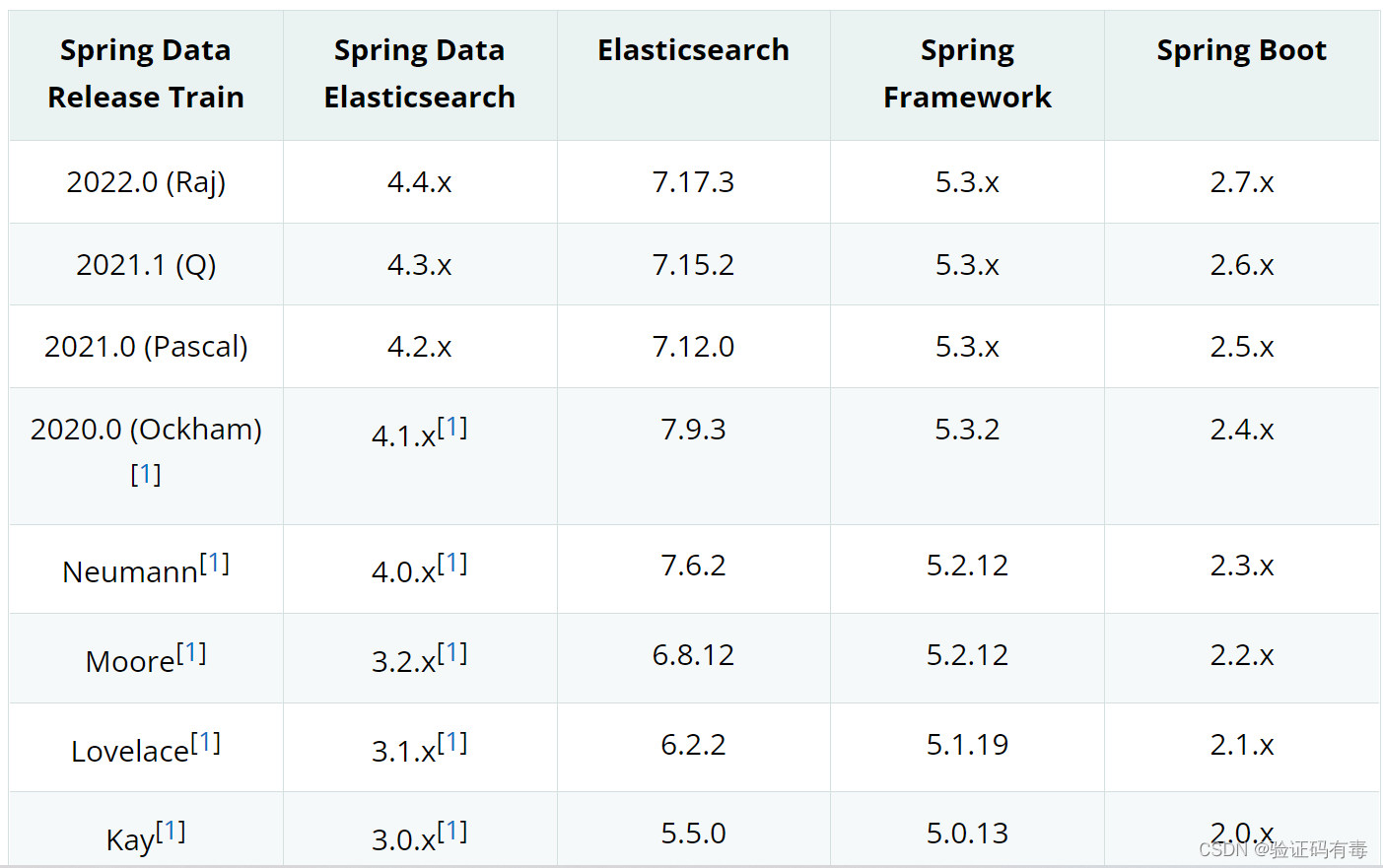
目录 前言从一个【搜索】说起 阅读对象阅读导航笔记正文一、全文检索1.1 什么是【全文检索】1.2 【全文检索】原理1.3 什么是倒排索引 二、ElasticSearch简介2.1 ElasticSearch介绍2.2 ElasticSearch应用场景2.3 数据库横向对比 三、ElasticSearch环境搭建3.1 Windows下安装3.2…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
