博弈论学习笔记(2)——完全信息静态博弈
前言
这部分我们学习的是完全信息静态博弈,主要内容包括博弈论的基本概念、战略式博弈、Nash均衡、Nash均衡解的特性、以及Nash均衡的应用。
零、绪论
1、什么是博弈论
1)博弈的定义
博弈论:研究决策主体的行为发生直接相互作用时候的决策以及这种决策的均衡问题。
完全理性的个人或群体发生直接相互作用的情形。博弈论研究这种情形下个人或群体的决策以及这种选择所导致的结果的理论。
2)博弈与传统决策的区别
传统的决策是从若干备选方案中选择一个有利方案,如出门带伞问题就是一个决策问题。而博弈是研究决策主体的行为发生直接相互作用时候的决策,在博弈中,决策主体的选择不仅与决策主体的偏好结构有关,而且与其他人的选择有关。
2、如何研究博弈论
1)完全理性假设的主要表现
-
参与人的偏好具有一致性
-
参与人对面临的决策问题具有完全的理解
-
参与人具有强大的逻辑推理能力和计算能力
2)共同知识是什么
如果有一种每个参与人都知道的“信息或事件”,并且每个参与人都知道每个参与人都知道它,每个参与人都知道每个参与人都知道每个参与人都知道它,……,如此等等,那么这种“信息”对于参与人而言就是共同知识。显然关于一个事件的共同知识这个概念比人们所熟悉的“相互知识”需要更多的信息,共同知识是无穷尽的“相互知识”。

有了参与人完全理性和参与人完全理性是共同知识这两个假设,就可以确保博弈过程的分析具有逻辑上的一致性。
3、博弈论研究的目的
1)什么是博弈问题的解
所有参与人都预测到的博弈结果,即参与人的一致性预测
将Nash均衡作为博弈问题的一致性预测,也就是博弈问题的解。
4、博弈论的主要分类
1)合作博弈与非合作博弈
决策主体的行为相互作用时,当事人能否达成一个具有约束力的协议。
2)静态博弈与动态博弈
根据参与人的先后顺序。
3)完全信息博弈与不完全信息博弈
参与人对其他参与人的特征,战略空间及支付函数在博弈开始时是否已知。
4)完美信息博弈与不完美信息博弈

注意完美信息博弈与完全信息博弈的比较
一、战略式博弈
1、基本概念
1)参与人
博弈中选择行动以最大化自己效用的决策主体
2)行动
参与人在博弈的某个时点的决策变量
3)行动组合(行动断面)
博弈中每个参与人采取一个行动的一种博弈情形
4)战略
参与人的行动规则,规定了参与人在每一种轮到自己行动的情形下,应该采取的行动。它是与博弈行动顺序相关的行动有序集,战略是行动的规则,而不是行动本身,作为行动规则,战略必须是完备的。
【特例】
在完全信息静态博弈中,不存在决策时序上的差异,所有参与人在同一决策时点即博弈开始那一时刻决策,因此所有参与人面临的决策情形只有一种。参与人的战略集与行动集相同。
5)战略组合
博弈中每个参与人采取战略组合中相应战略Si的一种博弈情形。
6)支付
参与人在博弈中的所得。参与人的支付就可表示为一种特定博弈情形(如行动组合或战略组合)下参与人得到的确定效用水平或期望效用水平。
7)信息
参与人所具有的有关博弈的所有的知识。
8)完美信息与完全信息

9)结果
博弈分析者所感兴趣的所有东西,如:均衡策略组合、均衡行动组合、均衡支付等。
10)均衡
所有参与人的最优的战略组合。在博弈论中,均衡是指所有个人的买卖规则(战略)的组合,均衡价格是这种战略组合的结果。
2、战略式博弈
1)战略式博弈的定义
战略式博弈是博弈问题的一种规范性描述,亦称为标准式博弈。
战略式博弈是一种相互作用的决策模型,这种模型假设每个参与人仅选择一次行动或行动计划(战略),并且这些选择是同时进行的。

二、Nash均衡
1、占优均衡
1)“囚徒困境”


理性的前提假设,使得每个小偷都有背离“抵赖,抵赖”的意愿,因此,小偷的选择会偏离“抵赖”,而选择“坦白”。

无论对方如何选择,每个小偷都会选择“坦白”,可以发现战略“坦白”具有这样的特点:无论对方怎样选择(选择“坦白”或者“抵赖”),“坦白”总是理性小偷的最优战略,而与其他小偷的选择无关。
在学习占优行为、重复剔除劣战略行为这章之前,不妨做一做下面这道题。
【收益矩阵的参数范围问题】
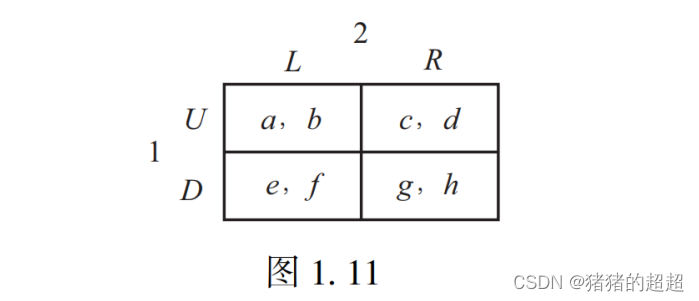
【题解】


2)占优战略
参与人的最优战略与其他参与人的选择无关。无论其他参与人选择什么战略,参与人的最优战略总是唯一的。这样的最优战略我们称为“占优战略”(dominant strategy)

3)占优行为
在一个博弈问题中,如果某个参与人具有占优战略,那么只要这个参与人是理性的,他肯定就会选择他的占优战略。参与人的这种选择行为我们称为占优行为。占优行为是理性参与人选择行为的最基本特征。
4)占优战略均衡
如果所有的参与人都具有占优战略,那么只要参与人是理性的,肯定都会选择自己的占优战略。
博弈的结果就由参与人的占优战略共同决定。像这种由参与人的占优战略共同决定的博弈结果,称为占优战略均衡(dominant-strategy equilibrium)。

2、重复剔除劣战略行为
1)劣战略

2)剔除劣战略行为

3)重复剔除的占优均衡

4)弱劣战略

5)均衡结果是否与劣战略的剔除顺序有关
一般而言,如果每次剔除的是严格劣战略,均衡结果与剔除顺序无关;如果剔除的是弱战略,均衡结果可能与剔除顺序有关
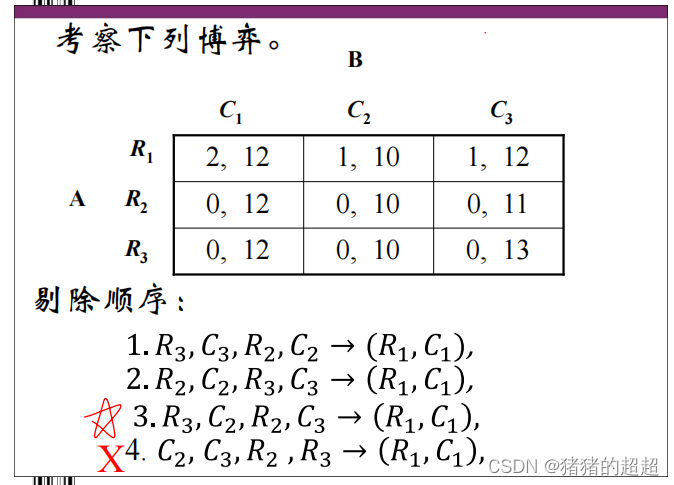
在重复剔除劣战略的过程中,需要注意:
-
重复剔除劣战略均衡要求“理性”为“共同知识” 。
-
一般而言,参与人的战略空间越大,需要剔除的步骤就越多,对“理性”的要求就越严格。
3、Nash均衡
1)什么是博弈问题的解
-
博弈分析是在博弈问题的结构和参与人完全理性为共同知识下进行的;
-
对博弈问题的求解,等同于完全理性的参与人对博弈的求解;
-
博弈问题的解:所有参与人的一致性预测。

2)什么是Nash均衡

3)求解Nash均衡的方法
【划线法】
在两人博弈中,相互构成最优战略的战略组合就是Nash均衡。

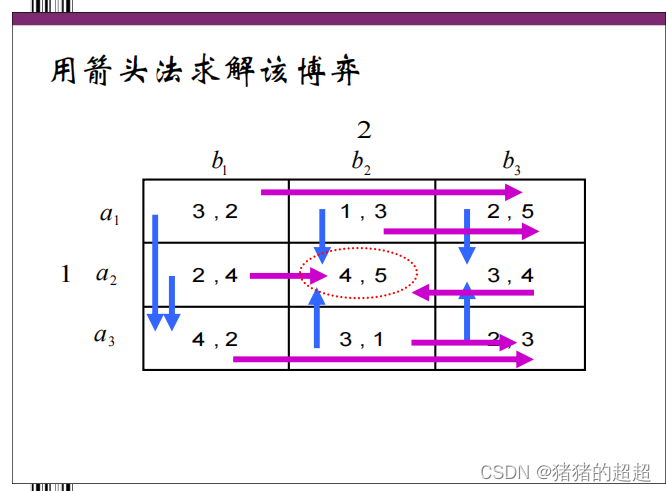
【箭头法】
在两人博弈中,一个战略组合只有在两个参与人都不愿意偏离的情况下才能构成Nash均衡。计算步骤如下:
-
对于每个战略组合,检查是否有参与人会偏离
-
找出没有参与人会偏离的战略组合
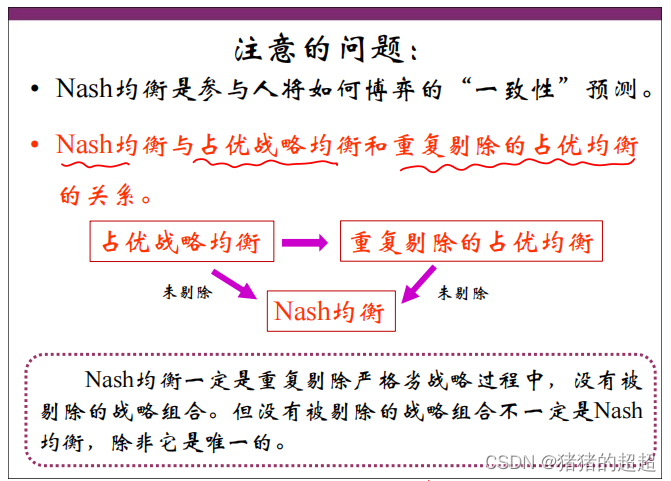
4)Nash均衡 VS 占优战略均衡 VS 重复剔除的占优均衡
4、混合战略Nash均衡
1)混合战略
以一定的概率分布来选择自己战略的行为,在博弈中称之为混合战略。与此相对应,参与人在给定信息下只选择一种特点战略,成为纯战略。

混合战略解释了一个参与人对其他参与人所采取的行动的不确定性,它描述了参与人在给定信息下以某种概率分布随机地选择不同的行动或战略。混合战略为定义在纯战略集上的一个概率分布。

2)混合战略的支付
对于混合战略,参与人的支付是不确定的,此时,参与人关心的是支付的期望收益。

3)混合战略与混合战略组合


4)纯战略-混合战略 VS 完全混合战略

5)混合战略Nash均衡

6)最优混合战略的特性


7)支集

8)最优反应的引理

5、混合战略Nash均衡的求解
1)等值法



【举例说明】

2)Wilson奇数定理

3)支撑是什么

掌握支撑的写法

4)支撑求解法

支撑法求解过程中可能遇到的问题:

5)支撑法求解典例








6)支撑法的问题,计算量大

用剔除劣战略的方法,排除支撑!!!
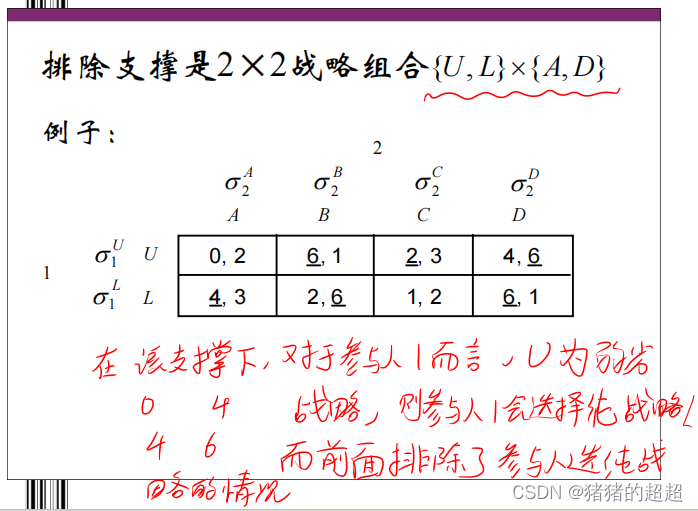
7)规划求解法


8)规划法求解典例
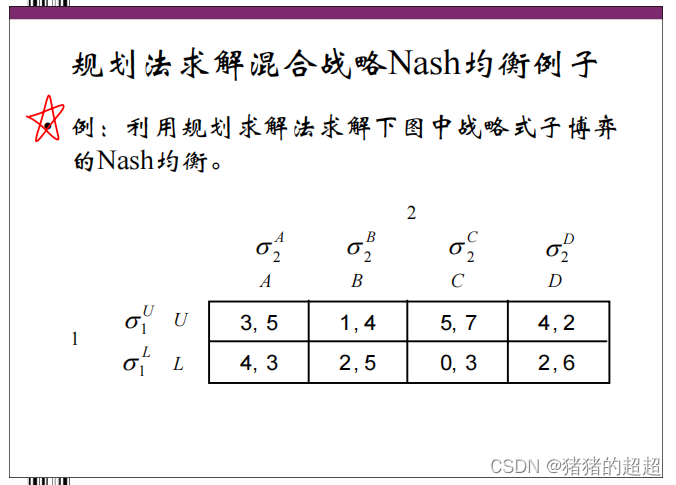



从理论上来讲,这两种方法对有限战略式博弈都是适用的,但从以上例子的求解过程来看,都存在着计算过程复杂,计算量大等问题,尤其是对多人(即参与人人数大于2)博弈问题。当参与人人数大于2时,使用支撑法,就必须求解非线性方程组;而使用规划法,就必须求解一个无论是目标函数还是约束条件都是非线性的规划问题。
三、Nash均衡解的特性
1、Nash均衡的意义
1)一致性预测
Nash均衡是博弈中的一种一致性预测——如果所有参与人预测一个特点的Nash均衡会出现,那么所有参与人都不会偏离,这个Nash均衡就会出现。

2)Nash均衡的特点
对任一个参与人i,在给定其他参与人选择的情况下,均衡战略是自己的最优战略。

3)一般解的定义



2、Nash均衡解的存在性
1)不同均衡概念之间的关系
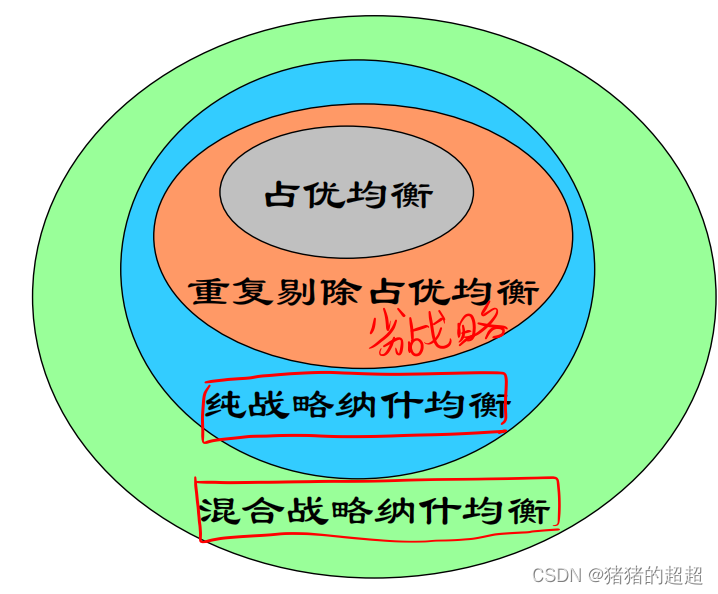
2)Nash均衡的存在性定理
每一个有限的战略式博弈至少存在一个Nash均衡(包括纯战略和混合战略Nash均衡)。
3、Nash均衡解的多重性

1)什么是Nash均衡的多重性问题
传统的博弈论研究的问题或许并不是如何找到博弈的Nash均衡(即存在性问题),而是在博弈的多个Nash均衡中选择一个合理的均衡(即多重性问题)。
但事实上,当在一个博弈中存在多个Nash均衡时,目前还没有一个一般的理论能证明哪个Nash均衡结果一定会出现。
2)如何解决Nash均衡的多重性问题
1、均衡精炼的方法
从博弈解的定义入手,在Nash均衡的基础上,通过定义更加精炼的博弈解如子博弈精炼Nash均衡、精炼贝叶斯Nash均衡等,剔除Nash均衡中不合理的均衡。这种解决Nash均衡多重性的思路具有普遍性,对所有的博弈问题都适用;
均衡精炼的方法可以称为规范式的方法,其它的方法称为非规范式的方法。
2、非规范式的方法
焦点效应
相关均衡
3)什么是焦点效应
在一个具有多重均衡的博弈中,趋向于将参与人的注意力集中到一个均衡的任何事情,都可能使参与人全都预期并随之实行这个均衡,就像一个自行应验的预言一样。
Schelling将这种现象称之为“焦点效应” (focal-point effect)。
在焦点效应中具有某种使它显著地区别于所有其它均衡性质的均衡,被称为“焦点均衡”(focal equilibrium)。
结合“性别战”的例子理解,详见PPT
-
博弈的现实状况或背景也会将博弈引向特定的均衡。
-
此外,“焦点效应”在某些博弈中还可能由均衡战略自身的性质来确定。
但是需要注意的是,聚焦因素只有针对Nash均衡时才可能是有效的。
4)什么是廉价磋商
类似于“性别战”中这种博弈之前进行的沟通或商议,在博弈分析中称之为具有通信的博弈或“廉价磋商”(cheap talk)。
在博弈分析中,将参与人在博弈开始之前,不花任何成本所达成的、对参与人没有约束力的协议称为“廉价磋商”。
5)什么是相关均衡
在“性别战”博弈中,夫妻双方通过长期的共处,在周末娱乐项目的选择上可能会形成这样的习惯:双方根据周末的天气状况来选择娱乐项目。
便得到了一种解决Nash均衡多重性问题的方式:让参与人根据某个共同观测到的信号(如“性别战”中的天气状况)来选择行动。
如果参与人根据信号选择行动的规则本身能够构成一个Nash均衡,那么参与人就可能会根据某个共同观测到的信号来选择行动。这种由参与人的行动规则所构成的Nash均衡,就是Aumann定义的“相关均衡”(correlated equilibrium)。

四、Nash均衡的应用
1、Cournot寡头竞争模型
该模型研究了寡头垄断市场中,企业追求利润最大化时的决策问题。
1)Cournot模型的基本假设

2)什么是反应函数

上面两个函数分别描述了给定对手的产量,企业 i 应该如何反应,因而分别称为企业1与企业2的反应函数(reaction function)。
反应函数意味着每个企业的最优产量是另一个企业的产量的函数,两个反应函数的交点便是Nash均衡点。
3)Cournot模型的计算



联合垄断市场、“垄断最优的情形在两个寡头的时候是无法达到”等内容详见PPT
2、Bertrand寡头竞争模型
在寡头垄断市场中,企业关心更多的可能是自己的产品在市场上的价格,而不是生产多少产品,也就是说,企业进行的可能是价格竞争而不是产量竞争。
1)Bertrand模型的基本假设

2)Bertrand模型的计算


3)Bertrand悖论


3、Hotelling寡头竞争模型
在Hotelling价格竞争模型中,Hotelling通过引入产品在空间位置上的差异,巧妙地解决了产品的差异形式的描述问题。
在Hotelling价格竞争模型中,产品虽然仍是同质的,但其在空间位置上有差异,因而对于不同位置的消费者其运输成本不同,由此导致产品不再是完全替代的。
1)Hotelling模型的基本假设

2)Hotelling模型的求解





通过引入产品的位置差异,使得企业的均衡利润不再为0,而企业的定价也大于产品的边际成本,在一定程度上解释了Bertrand悖论。
在上面的分析中,我们将两个企业固定于线性城市的两端。如果允许企业在选择价格的同时还可以选择位置,那么两个企业都会选择线性城市的中点(即[0,1]区间的中点),而当两个企业都位于中点时,Bertrand均衡则成为模型的唯一均衡。
4、Hardin公共财产问题
公共资源被过度使用,如草原沙化,渔业资源枯竭以及各种矿产资源的过度开发等等,使人类社会的生存面临着极大的挑战。以G. Hardin的公共财产模型为例,分析人们的利己行为如何使得公共资源被过度使用。


具体求解过程详见PPT
5、混合战略Nash均衡的应用
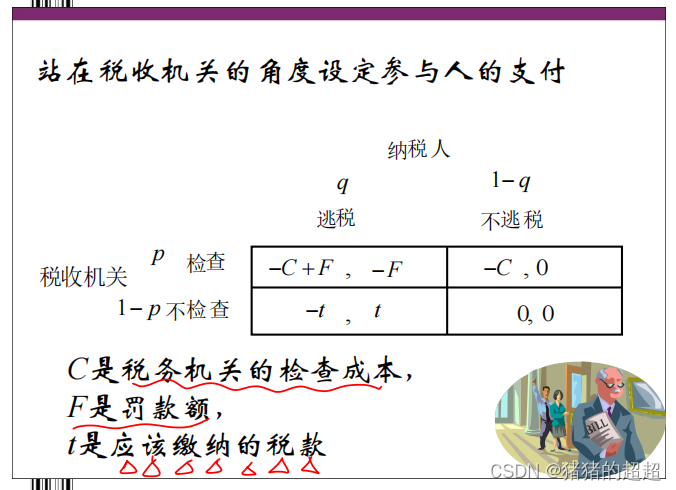
1)小偷-守卫博弈
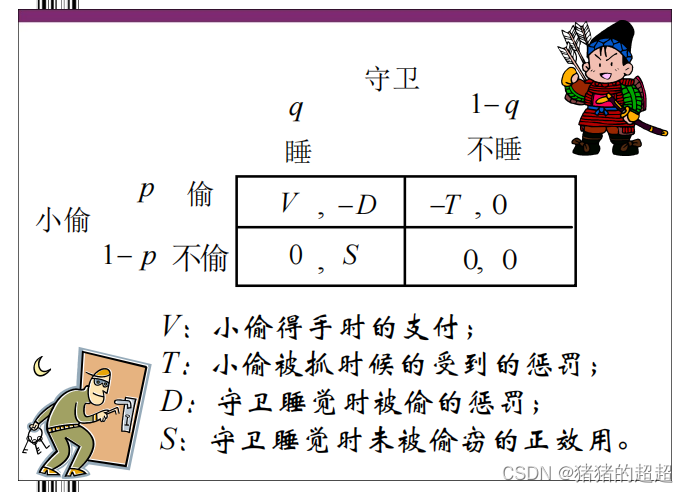
2)监督博弈

相关文章:

博弈论学习笔记(2)——完全信息静态博弈
前言 这部分我们学习的是完全信息静态博弈,主要内容包括博弈论的基本概念、战略式博弈、Nash均衡、Nash均衡解的特性、以及Nash均衡的应用。 零、绪论 1、什么是博弈论 1)博弈的定义 博弈论:研究决策主体的行为发生直接相互作用时候的决策…...

【COMP304 LEC4 LEC5】
LEC 4 1. Truth-Functionality Propositional logic 的connectives(连接词)are truth-functional 但是,有时候的描述不是true-functional的,比如:"Knowing that", "It is necessary that",&quo…...

表白墙(服务器)
目录 0.需求 1.创建Maven项目 2.给pom.xml内引入三个依赖 3.完善目录,并补充web.xml中的内容 4.编写代码 后端代码 编辑前端代码 5.引入数据库 创建message表 创建工具类 往MessageServlet类中添加方法 0.需求 前面写好了表白墙页面,但存…...

在 Mac 中卸载 Node.js
在 Mac 中卸载 Node.js,可以选择以下两种方法: 使用命令行卸载 Node.js 第一步:打开终端,输入以下命令显示 Node.js 的安装路径: which node 执行该命令后,会显示安装路径:/usr/local/bin/n…...

Hafnium构建选项及FVP模型调用
安全之安全(security)博客目录导读 目录 一、Hafnium构建选项 二、FVP模型调用 一、Hafnium构建选项 本节解释了在支持基于FF-A的SPM (SPMD位于EL3, SPMC位于S-EL1、S-EL2或EL3)的情况下进行构建时涉及的TF-A构建选项:...

第44天:前端及html、Http协议
前端 前端是所有跟用户直接打交道的都可以称之为是前端,比如:PC页面、手机页面、平板页面、汽车显示屏、大屏幕展示出来的都是前端内容。 前端的用处: 学了前端以后我们就可以做全栈工程师(会后端、会前端、会DB、会运维等),能够写一些简单的…...

shell_63.Linux产生信号
Linux 系统信号 信号 值 描述 1 SIGHUP 挂起(hang up)进程 2 SIGINT 中断(interrupt)进程 3 SIGQUIT 停止(stop)进程 9 …...
)
互联网摸鱼日报(2023-11-01)
互联网摸鱼日报(2023-11-01) 36氪新闻 毫末智行张凯:2023年高阶智能辅助驾驶市场迎来大爆发 撕开三星、金士顿市场,国产老牌存储器企业出海三年,营收翻三倍|insight全球 给医生一双“透视眼”,「锦瑟医疗」专注开…...

AR的光学原理?
AR智能眼镜的光学成像系统 AR眼镜的光学成像系统由微型显示屏和光学镜片组成,可以将其理解为智能手机的屏幕。 增强现实,从本质上说,是将设备生成的影像与现实世界进行叠加融合。这种技术基本就是通过光学镜片组件对微型显示屏幕发出的光线…...

语义分割 实例分割的异同点
语义分割和实例分割是计算机视觉领域中两个相关但不同的任务,它们都涉及对图像像素进行分类和标记,但关注的对象和目标有所不同。 目标对象: 语义分割:语义分割的目标是将图像中的每个像素标记为对应的语义类别,即将…...

C++学习初探---‘C++面向对象‘-继承函数重载与运算符重载
文章目录 前言继承继承是什么?三种访问权限的继承: 函数重载与运算符重载函数重载运算符重载可重载运算符&不可重载运算符 前言 第三次学习记录,依旧是C面向对象的内容。 继承 继承是什么? C中的继承是一种面向对象编程&am…...

Linux下搭建SRS服务器环境
搭建环境 Ubuntu的Linux环境srs 安装源码:源码地址为:GitHub - ossrs/srs at 3.0release 搭建步骤 下载srs源码 git clone GitHub - ossrs/srs: SRS is a simple, high-efficiency, real-time video server supporting RTMP, WebRTC, HLS, HTTP-FLV,…...
)
pytest 使用(一)
pytest 使用pytest,默认的测试用例的规则以及基础应用pytest测试用例的运行方式pytest执行测试用例的顺序是怎样的呢?如何分组执行(冒烟,分模块执行,分接口和web执行)pytest跳过测试用例 b站课程链接 使用…...

基于秃鹰算法的无人机航迹规划-附代码
基于秃鹰算法的无人机航迹规划 文章目录 基于秃鹰算法的无人机航迹规划1.秃鹰搜索算法2.无人机飞行环境建模3.无人机航迹规划建模4.实验结果4.1地图创建4.2 航迹规划 5.参考文献6.Matlab代码 摘要:本文主要介绍利用秃鹰算法来优化无人机航迹规划。 1.秃鹰搜索算法 …...
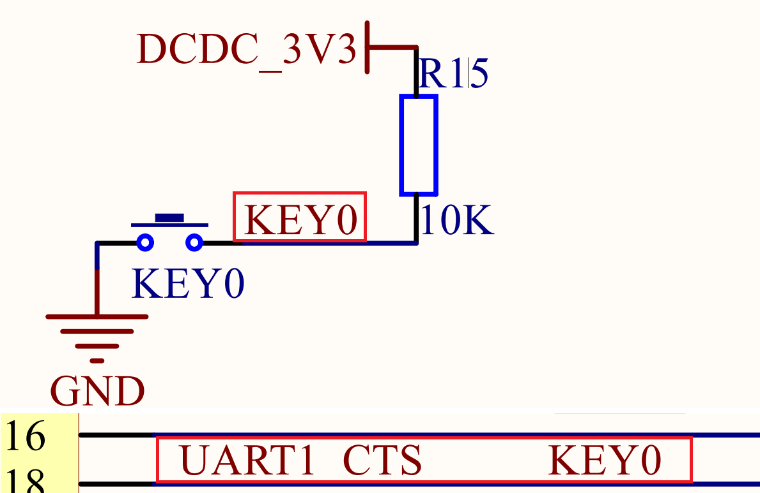
08. 按键输入
08. 按键输入 按键原理图代码编写GPIO驱动代码按键驱动代码主函数 加上清除BSS段,代码不运行 按键原理图 按键KEY0连接到了UART1_CTS上。默认情况下,KEY0为高,当按下KEY0后,UART1_CTS为低电平 代码编写 在bsp下创建一个key和一个…...

YOLOv8-pose关键点检测:模型轻量化创新 |轻量高性能网络PPLCNet助力backbone
💡💡💡本文解决什么问题:轻量高性能网络PPLCNet替换YOLOv8 backbone PPLCNet | GFLOPs从9.6降低至6.6, mAP50从0.921下降至0.901,mAP50-95从0.697提升至0.752 Yolov8-Pose关键点检测专栏介绍:https://blog.csdn.net/m0_63774211/category_12398833.html ✨✨✨手…...

大数据笔记-关于Cassandra的删除问题
Cassandra是Facebook开源的一个NoSQL数据库,它除了具备一般的NoSQL分布式数据库特点以外,最大的一个特点是去中心化架构设计,这和Hadoop HDFS/HBase等不一样,比如HDFS分为NameNode和DataNode,而Cassandra集群中所有节点…...

Qt自定义文件选择框
文章目录 前言一、头文件二、源文件三、qss文件四、效果 前言 在开发过程中,经常遇到使用文件选择框的情况,qt默认的文件选择框,样式可能与开发的桌面程序差异比较大.此时,我们可以自定义文件选择框,设置其样式,尽量做到样式统一. 一、头文件 #ifndef CUSTOMFILEDIALOG_H #d…...
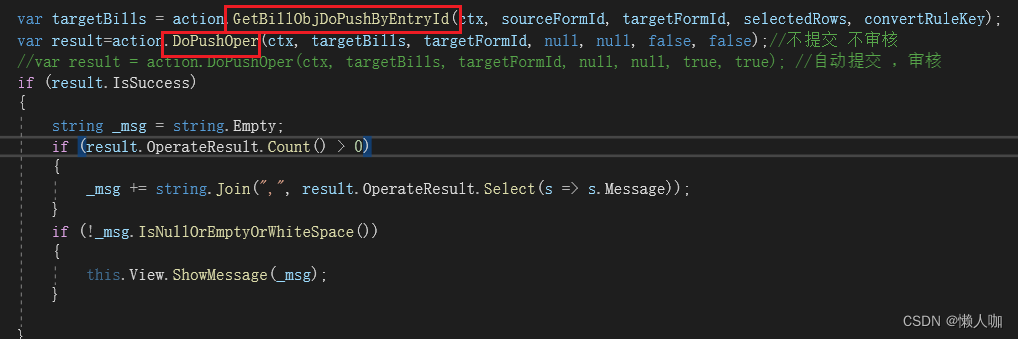
金蝶云星空创建自动下推并保存公共服务
文章目录 金蝶云星空创建自动下推并保存公共服务创建公共方法按单下推数据按明细行下推数据调用下推操作 调用公共方法 金蝶云星空创建自动下推并保存公共服务 创建公共方法 按单下推数据 /// <summary>/// 获取单据转换数据包/// </summary>public DynamicObjec…...

人大金仓助力中国人民银行征信中心业务系统异地容灾优化升级
日前,人大金仓助力中国人民银行应收账款融资服务平台异地容灾项目顺利上线,保证了平台系统运行的连续性和数据安全,为充分发挥平台的融资功能,缓解中小微企业融资难提供了强有力的保障。 缓解中小微企业融资难 中国人民银行构于2…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...





