Python自动化测试面试题-编程篇
前言
随着行业的发展,编程能力逐渐成为软件测试从业人员的一项基本能力。因此在笔试和面试中常常会有一定量的编码题,主要考察以下几点。
- 基本编码能力及思维逻辑
- 基本数据结构(顺序表、链表、队列、栈、二叉树)
- 基本算法(排序、查找、递归)及时间复杂度
除基本算法之外,笔试面试中经常会考察以下三种思想:
- 哈希
- 递归
- 分治
哈希
哈希即Python中的映射类型,字典和集合,键值唯一,查找效率高,序列(列表、元祖、字符串)的元素查找时间复杂度是O(n),而字典和集合的查找只需要O(1)。
因此哈希在列表问题中主要有两种作用:
- 去重
- 优化查找效率
列表去重
列表去重在不考虑顺序的情况下可以直接使用set()转换(转换后会自动排序),需要保持顺序可以使用字典构建的fromkeys()方法,利用字典键值的唯一性去重。
不考虑顺序:
l = [2,1,2,3,4,5,6,6,5,4,3,2,1]
result = list(set(l))
print(result)运行结果:
[1, 2, 3, 4, 5, 6]考虑顺序:
l = [2,1,2,3,4,5,6,6,5,4,3,2,1]
s = set()
result = []
for i in l:if i in s:continues.add(i)result.append(i)
print(result)注意,这里如果使用:
if not i in result:result.append(i)虽然看起来代码简单,但是列表in查找的的时间复杂度为O(n),not in的效率比in要差,每次都要进行n次比对。
上例中,使用了一个集合变量s来优化in查找,同时使用in代替not in。
Python3.6后字典按键值插入顺序,如果使用Python3.6,也可以利用字典的有序性来去重,示例如下:
l = [2,1,2,3,4,5,6,6,5,4,3,2,1]
result = list({}.fromkeys(l).keys())
print(result)运行结果:
[2, 1, 3, 4, 5, 6]列表分组
一串字母数字组合的字符串,找出相同的字母或数字,并按照个数排序。
l = [1,2,3,'a','b','c',1,2,'a','b',3,'c','d','a','b',1]
set1 = set(l)
result = [(item, l.count(item)) for item in set1]
result.sort(key=lambda x:x[1], reverse=True)
print(result)这里使用哈希的键值不重复性。当然也可以使用python自带的groupby函数,代码如下:
from itertools import groupbyl = [1,2,3,'a','b','c',1,2,'a','b',3,'c','d','a','b',1]
l.sort(key=lambda x: str(x)) # 分组前需要先排序
result = []
for item, group in groupby(l, key=lambda x: str(x)):result.append((item, len(list(group))))
result.sort(key=lambda x:x[1], reverse=True)
print(result)海量数据top K
对于小数据量可以使用排序+切片,而对于海量数据,需要考虑服务器硬件条件。即要考虑时间效率,也要考虑内存占用,同时还要考虑数据特征。如果大量的重复数据,可以先用哈希进行去重来降低数据量。
这里我们使用生成器生成1000万个随机整数,求最大的1000个数,生成随机数的代码如下:
import random
import time
n = 10000 * 1000
k = 1000
print(n)
def gen_num(n):for i in range(n):yield random.randint(0, n)
l = gen_num(n)- 不限内存可以直接使用set()去重+排序
start = time.time()
l = list(set(l))
result = l[-k:]
result.reverse()
print(time.time()-start)1000w个数据会全部读入内存,set后列表自动为递增顺序,使用切片取-1000到最后的即为top 1000的数
- 使用堆排可以节省一些内存
start = time.time()
result = heapq.nlargest(k, l)
print(time.time()-start)这里是用来Python自带的堆排库heapq。使用nlargest(k,l)可以取到l序列,最大的k个数。
- 较小内存可以分治策略,使用多线程对数据进行分组处理(略)
两数之和
l=[1,2,3,4,5,6,7,8] 数据不重复,target=6,快速找出数组中两个元素之和等于target 的数组下标。
注意,不要使用双重循环,暴力加和来和target对比,正确的做法是单层循环,然后查找target与当前值的差,是否存在于列表中。
但是由于列表的in查询时间复杂度是O(n),即隐含了一层循环,这样效率其实和双重循环是一样的,都是O(n^2)。
这里就可以使用哈希来优化查询差值是否在列表中操作,将O(n)降为O(1),因此总体的效率就会变成O(n^2)->O(n)。
l = [1,2,3,4,5,6,7,8]
set1 = set(list1) # 使用集合已方便查找
target = 6result = []
for a in set1:b = target - aif a < b < target and b in set1: # 在集合中查找,为避免重复,判断a为较小的那个值result.append((list1.index(a), list1.index(b))) # 列表index取下标的操作为O(1)
print(result)递归问题
递归是一种循环调用自身的函数。可以用于解决以下高频问题:
- 阶乘
- 斐波那切数列
- 跳台阶、变态跳台阶
- 快速排序
- 二分查找
- 二叉树深度遍历(前序、中序、后序)
- 求二叉树深度
- 平衡二叉树判断
- 判断两颗树是否相同
递归是一种分层推导解决问题的方法,是一种非常重要的解决问题的思想。递归可快速将问题层级化,简单化,只需要考虑出口和每层的推导即可。
如阶乘,要想求n!,只需要知道前一个数的阶乘(n-1)!,然后乘以n即可,因此问题可以转为求上一个数的阶乘,依次向前,直到第一个数。
举个通俗的例子:
A欠你10万,但是他没那么多钱,B欠A 8万,C欠B 7万 C现在有钱。因此你要逐层找到C,一层一层还钱,最后你才能拿到属于你的10万。
编写递归函数有两个要点:
- 出口条件,可以不止一个
- 推导方法(已知上一个结果怎么推导当前结果)
阶乘
求n的阶乘
- 出口:n = 1 时,返回1
- 推导:(n-1)层的结果 * n
代码如下:
def factorial(n):if n == 1: # 出口return 1return factorial(n-1) * n # 自我调用求上一个结果,然后推导本层结果也可以简写为 factorial = lambda n: 1 if n==1 else factorial(n-1) * n
斐波那切数列
斐波那切数列是 1 1 2 3 5 8 ...这样的序列。前两个数为1,后面的数为前两个数之和。
- 出口:n <= 2,返回1
- 推导:(n-1)层的结果 + (n-2)层的结果
代码如下:
def fib(n):if n<=2:return 1return fib(n-2) + fib(n-1) 递归是一种分层简化问题的解法,但不一定是效率最高的解法,比如斐波那切数列中,在求fib(n-2) 和 fib(n-1)时实际上反复求解了两次fib(n-2)。
可以通过缓存来优化效率,代码如下。
from functools import lru_cache@lru_cache()
def fib(n):if n<=2:return 1return fib(n-2) + fib(n-1) 跳台阶、变态跳台阶
- 跳台阶:一只青蛙,一次可以跳上1阶,也可以跳上2阶,问跳上n阶有多少种跳法。
- 变态跳台阶:一只青蛙,一次可以跳上1阶,可以一次跳上n阶,为跳上n阶有多少种跳法。
这个问题关键是逻辑分析每层的推导过程。
跳台阶实际上就是一个从第二位开始的斐波那切数列:1 2 3 5 8 13 ...
- 出口:n <= 2,返回n(即1时返回1,2时返回2)
- 推导:(n-1)层的结果 + (n-2)层的结果
代码如下:
jump1 = lambda n: n if n<=2 else jump1(n-2) + jump1(n-1)变态跳台阶只是推导方式不同,每一层的结果是上一层跳法的2倍。
- 出口:n <= 2,返回n
- 推导:(n-1)层的结果 * 2
代码如下:
jump2 = lambda n: n if n<=2 else jump2(n-1) * 2
快速排序
快速排序的是想是选一个基准数(如第一个数),将大于该数和小于该数的分成两块,然后在每一块中重复执行此操作,直到该块中只有一个数,即为有序。
- 出口:列表长度为1(<2)时,返回列表
- 选择一个数,(将小于该数的序列)排序结果 + 基准数 + (大于该数的序列)排序结果
def quick_sort(l): if len(l) < 2:return ltarget = l[0] # 以第一个数为基准数low_part, eq_part, high_part = [], [target], []for i in l[1:]:if i < target:low_part.append(i)elif i == target:eq_part.append(i)else:high_part.append(i)return quick_sort(low_part) + eq_part + quick_sort(high_part)注:eq_part中应包含基准数target。
二分查找
二分查找需要序列首先有序。思想是先用序列中间数和目标值对比,如果目标值小,则从前半部分(小于中间数)重复此查找,否则从后半部分重复此查找。
- 出口1:中间数和目标数相同,返回中间数下标
- 出口2:列表为空,返回未找到
- 推导:
def bin_search(l, n): if not l:return Nonemid = len(l) // 2if l[mid] == n:return midif l[mid] > n:return bin_search(l[:mid])return bin_search(l[mid+1:])二叉树遍历
二叉树是非常常考的一种数据结构。其基本结构就是一个包含数据和左右节点的一种结构,使用Python类描述如下:
class Node(object):def __init__(self, data, left=None, right=None):self.data = dataself.left = leftself.right = right二叉树的遍历分为分层遍历(广度优先)和深度遍历(深度优先)两种,其中深度遍历又分为前序、中序、后序三种。
分层遍历由于每次处理多个节点,使用循环解决更加方便一点(也可以是使用递归解决)。
分层遍历代码如下:
def lookup(root):row = [root]while(row):print(row)row = [kid for item in row for kid in (item.left, item.right) if kid]’深度遍历
- 出口:节点为None
- 推导:
- 前序:打印当前节点-》遍历左子树 -》遍历右子树
- 中序:遍历左子树 -》打印当前节点-》遍历右子树
- 后序:遍历左子树 -》遍历右子树-》打印当前节点
以前序为例:
def deep(root):if root is none:return[print(root.data), deep(root.left), deep(root.right)]二叉树最大深度
二叉树最大深度即其左子树深度和右子树深度中最大的一个加上1(当前节点)。由于二叉树的每一个左右节点都是一个二叉树,这种层层嵌套的结构非常适合使用递归求解。
- 出口:节点为空,深度返回0
- 推导:左子树深度和右子树深度中最大的一个 + 1
def max_depth(root):if not root:return 0return max([max_depth(root.left), max_depth(root.right)]) + 1相等二叉树判断
相等二叉树是只,一个二叉树,节点数据相同,左右子树也完全相同。由于左右子树也是一个二叉树,因此也可以使用递归求解。
- 出口:最后的节点都为None时,两个相等,返回True
- 推导:判断两个节点数据是否相等,左子树是否相等(递归),右子树是否相等(递归)
def is_same_tree(p, q):if p is None and q is None:return Trueelif p and q:return p.data == q.data and is_same_tree(p.left, q.left) and is_same_tree(p.right, q.right)平衡二叉树判断
平衡二叉树是指,一个二叉树的左右子树的高度差不超过1。平衡二叉树的左右子树也应该是平衡二叉树,因此这也是一个递归问题。
- 出口:两个节点都为None时,返回True(平衡)
- 判断左子树和右子树深度的差<=1,并且左右子树都是平衡二叉树(递归)
注:这里需要使用以上求二叉树深度的方法
def max_depth(root):if not root:return 0return max([max_depth(root.left), max_depth(root.right)]) + 1def is_balance_tree(root):if root is None:return Truereturn abs(max_depth(root.left)-max_depth(root.right))<=1 and is_balance_tree(root.left) and is_balance_tree(root.right)其他
字符串统计
str1 = 'abcdaacddceea'
set1 = set(str1)
result = [(char, str1.count(char)) for char in set1]
print(result)统计重复最多的n个字符
统计重复最多的n个字符#
Copy
from collections import Counter
c = Counter('abcdaacddceea')
print(c.items())
print(c.most_common(3))字符串反转
- 简单字符串反转
Python中字符串反转方式非常多,而且比较高效,可以使用反向切片或者reverse实现。
'abcefg'[::-1]或
''.join(reversed('abcdefg'))- 包含数字字母的字符串,仅反转字母
可以通过遍历判断,如果是字母则取其对应反转索引位置的字母,如果是数字则取当前数字。
a = 'abc123efg'
l = len(a)
r = []
for i,c in enumerate(a):r.append(c) if c.isdigit() else r.append(a[l-i-1])
print(''.join(r))判断括号是否闭合
这是栈使用的一个经典示例,思路为,遇到正括号则入栈,遇到反括号则和栈顶判断,如果匹配则匹配的正括号出栈(完成一对匹配),否则打印不匹配,break退出。
text = "({[({{abc}})][{1}]})2([]){({[]})}[]"def is_closed(text)stack = [] # 使用list模拟栈, stack.append()入栈, stack.pop()出栈并获取栈顶元素brackets = {')':'(',']':'[','}':'{'} # 使用字典存储括号的对应关系, 使用反括号作key方便查询对应的括号for char in text:if char in brackets.values(): # 如果是正括号,入栈stack.append(char)elif char in brackets.keys(): # 如果是反括号if brackets[char] != stack.pop(): # 如果不匹配弹出的栈顶元素return Falsereturn Trueprint(is_closed(text))合并两个有序列表,并保持有序
常见的解法有两种:
- 连接 + 排序,时间复杂度度为O((m+n)log2(m+n))
- 两个队列根据大小依次弹出,时间复杂度度约为O(m+n)
依次出队列的逻辑为:
- 队列1为空,队列2不为空,从队列2弹出一个数据
- 队列2为空,队列1不为空,从队列1弹出一个数据
- 两个都不为空,判断两个对队列顶端哪个小,从哪个列表弹出一个数据
以下为使用Python列表模拟两个队列依次弹出的示例。
由于Python列表尾部弹出list.pop()的的操作效率O(1),比首部弹出list.pop(0)的操作效率O(n)更高,因此我们先按从大到小排序,最后在执行一次反转。
list1 = [1,5,7,9]
list2 = [2,3,4,5, 6,8,10,12,14]
result = []
for i in range(len(list1) + len(list2)):if list1 and not list2:result.append(list1.pop())elif list2 and not list1:result.append(list2.pop())else:result.append(list1.pop()) if list1[-1] > list2[-1] else result.append(list2.pop()) # 弹出顶端大的数
result.reverse() # 执行反转
print(result)两个队列实现一个栈
队列是先入先出,栈是先入后出。
使用两个队列实现栈的方式有很多种,主要分为优化入栈和优化出栈两种,以下为优化入栈的一种实现方法。
- 入栈时直接存入队列q1
- 出栈时,将q1中元素依次放入q2, 直到最后一个元素,弹出元素,然后将q2中元素重新依次放回q1
实现代码如下:
import queueclass Stack(object):def __init__(self):self.q1 = queue.Queue()self.q2 = queue.Queue()def push(self, value):self.q1.put(value)def pop(self):while self.q1.qsize() > 1:self.q2.put(self.q1.get())value = self.q1.get()while not self.q2.empty():self.q1.put(self.q2.get())return value测试代码:
s = Stack()
[s.push(i) for i in [1,2,3,4,5,6,7]]
print(s.pop())
print(s.pop())
print(s.pop())
print(s.pop())打印结果为:
7
6
5
4相关文章:

Python自动化测试面试题-编程篇
前言 随着行业的发展,编程能力逐渐成为软件测试从业人员的一项基本能力。因此在笔试和面试中常常会有一定量的编码题,主要考察以下几点。 基本编码能力及思维逻辑基本数据结构(顺序表、链表、队列、栈、二叉树)基本算法…...

CIT 594 Module 7 Programming AssignmentCSV Slicer
CIT 594 Module 7 Programming Assignment CSV Slicer In this assignment you will read files in a format known as “comma separated values” (CSV), interpret the formatting and output the content in the structure represented by the file. Q1703105484 Learning …...
链路追踪——【Brave】第一遍小结
前言 微服务链路追踪系列博客,后续可能会涉及到Brave、Zipkin、Sleuth内容的梳理。 Brave 何为Brave? github地址:https://github.com/openzipkin/brave Brave是一个分布式追踪埋点库。 #mermaid-svg-riwF9nbu1AldDJ7P {font-family:"…...
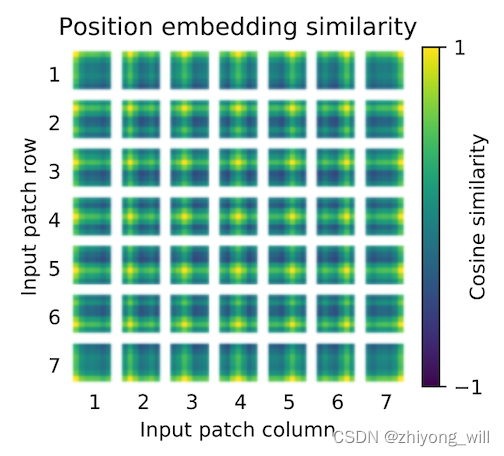
Vision Transformer(ViT)
1. 概述 Transformer[1]是Google在2017年提出的一种Seq2Seq结构的语言模型,在Transformer中首次使用Self-Atttention机制完全代替了基于RNN的模型结构,使得模型可以并行化训练,同时解决了在基于RNN模型中出现了长距离依赖问题,因…...

104-JVM优化
JVM优化为什么要学习JVM优化: 1:深入地理解 Java 这门语言 我们常用的布尔型 Boolean,我们都知道它有两个值,true 和 false,但你们知道其实在运行时,Java 虚拟机是 没有布尔型 Boolean 这种类型的&#x…...

QML 颜色表示法
作者: 一去、二三里 个人微信号: iwaleon 微信公众号: 高效程序员 如果你经常需要美化样式(最常见的有:文本色、背景色、边框色、阴影色等),那一定离不开颜色。而在 QML 中,颜色的表示方法有多种:颜色名、十六进制颜色值、颜色相关的函数,一起来学习一下吧。 老规矩…...
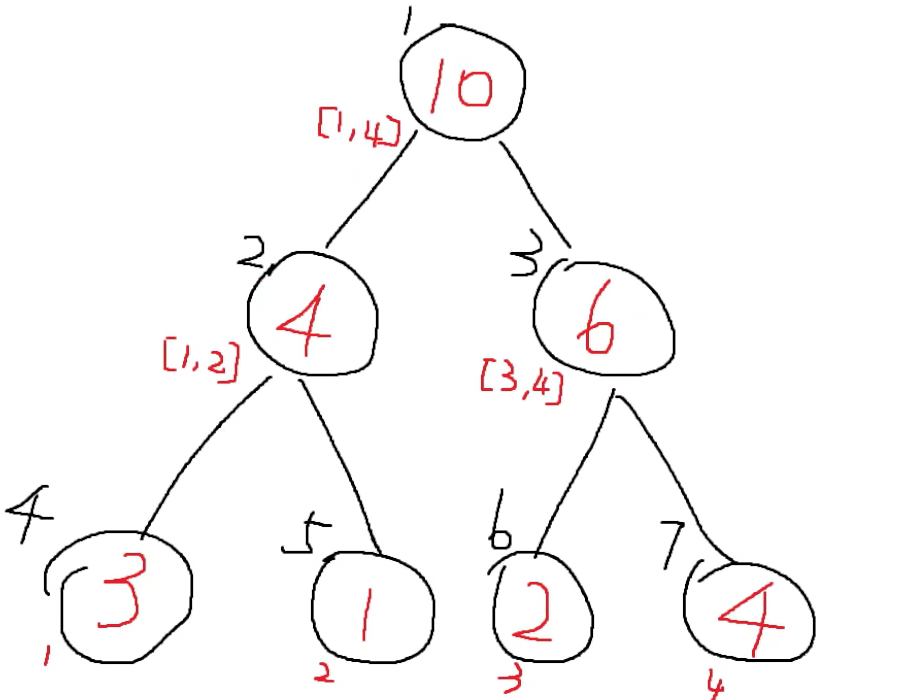
基础数据结构--线段树(Python版本)
文章目录前言特点操作数据存储updateLazy下移查询实现前言 月末了,划个水,赶一下指标(更新一些活跃值,狗头) 本文主要是关于线段树的内容。这个线段树的话,主要是适合求解我们一个数组的一些区间的问题&am…...

【micropython】SPI触摸屏开发
背景:最近买了几块ESP32模块,看了下mircopython支持还不错,所以买了个SPI触摸屏试试水,记录一下使用过程。硬件相关:SPI触摸屏使用2.4寸屏幕,常见淘宝均可买到,驱动为ILI9341,具体参…...
【云原生】k8s中Pod进阶资源限制与探针
一、Pod 进阶 1、资源限制 当定义 Pod 时可以选择性地为每个容器设定所需要的资源数量。 最常见的可设定资源是 CPU 和内存大小,以及其他类型的资源。 当为 Pod 中的容器指定了 request 资源时,调度器就使用该信息来决定将 Pod 调度到哪个节点上。当还…...
AI - stable-diffusion(AI绘画)的搭建与使用
最近 AI 火的一塌糊涂,除了 ChatGPT 以外,AI 绘画领域也有很大的进步,以下几张图片都是 AI 绘制的,你能看出来么? 一、环境搭建 上面的效果图其实是使用了开源的 AI 绘画项目 stable-diffusion 绘制的,这是…...
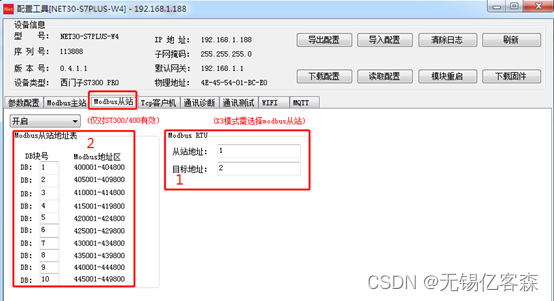
应用场景五: 西门子PLC通过Modbus协议连接DCS系统
应用描述: 西门子PLC(S7200/300/400/200SMART)通过桥接器可以支持ModbusRTU串口和ModbusTCP以太网(有线和无线WIFI同时支持)两种通讯方式连接DCS系统,不需要编程PLC通讯程序,直接在模块中进行地…...

我继续问了ChatGPT关于SAP顾问职业发展前景的问题,大家感受一下
目录 SAP 顾问 跟其他IT工作收入情况相比是怎么样的? 如何成为SAP FICO 优秀的顾问 要想成为SAP FICO 优秀的顾问 ,需要ABA开发技能吗 SAP 顾问中哪个类型收入最多? 中国的ERP软件能够取代SAP吗? 今天我继续撩 ChatGPT。随便问…...
)
Python小白入门---00开篇介绍(简单了解一下)
Python 小白入门 系列教程 第一部分:Python 基础 介绍 Python 编程语言安装 Python 环境变量和数据类型运算符和表达式控制流程语句函数和模块异常处理 第二部分:Python 标准库和常用模块 Python 标准库简介文本处理和正则表达式文件操作和目录操作时…...

【算法基础】C++STL容器
一、Vector 1. 初始化(定义) (1)vector最基本的初始化: vector <int> a;(2)定义长度为10的vector: vector <int> a(10);(3)定义长度为10的vector,并且把所有元素都初始化为-3: vector <int...

【经典蓝牙】蓝牙 A2DP协议分析
A2DP 介绍 A2DP(Advanced Audio Distribution Profile)是蓝牙高音质音频传输协议, 用于传输单声道, 双声道音乐(一般在 A2DP 中用于 stereo 双声道) , 典型应用为蓝牙耳机。 A2DP旨在通过蓝牙连接传输高质量的立体声音…...
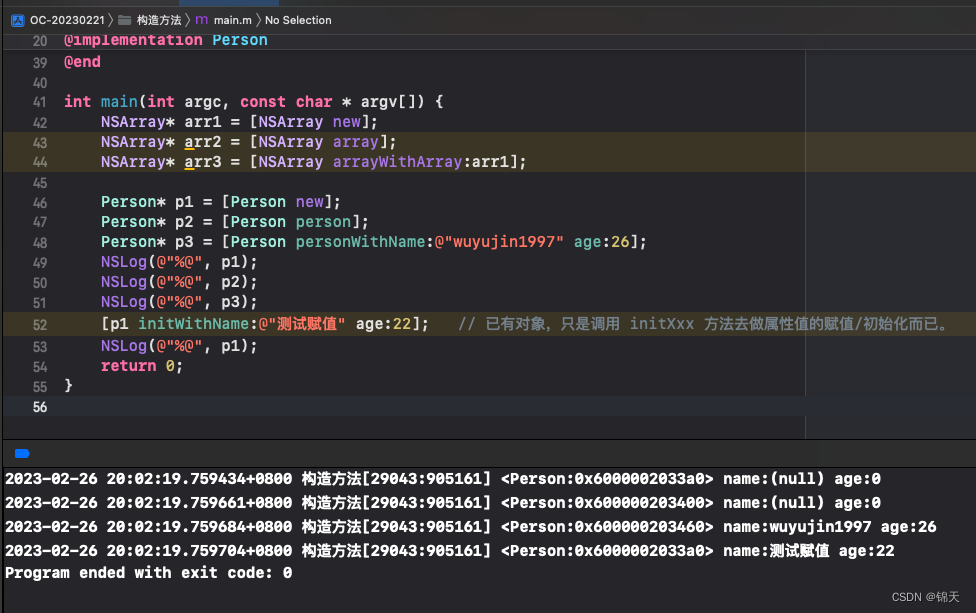
Objective-C 构造方法的定义和声明规范
总目录 iOS开发笔记目录 从一无所知到入门 文章目录源码中 NSArray 的构造方法与命名规律自定义类的构造方法命名截图代码输出源码中 NSArray 的构造方法与命名规律 interface NSArray<ObjectType> (NSArrayCreation) (instancetype)array;(instancetype)arrayWithObject…...

Matlab图像处理学习笔记
Matlab图像处理 Matlab基础 数组 1、向量 生成方式1: x = [值] x = [1 2 3] % 行向量 y = [4; 5; 6] % 列向量 z = x % 行向量转列向量...
——迭代器的基础理论知识)
笔记(三)——迭代器的基础理论知识
迭代器是一种检查容器内元素并且遍历容器内元素的数据类型。它提供对一个容器中的对象的访问方法,并且定义了容器中对象的范围。一、vector容器的iterator类型vector容器的迭代器属于随机访问迭代器,一次可以移动多个位置。vector<int>::iterator …...
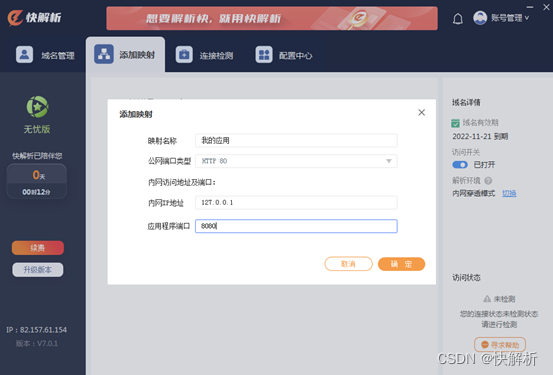
没有公网ip怎么外网访问nas?快解析内网端口映射到公网
对于NAS用户而言,外网访问是永远绕不开的话题。拥有NAS后的第一个问题,就是搞定NAS的外网访问。不过众所周知,并不是所有的小伙伴都能得到公网IP,由于IPV4资源的枯竭,一般不会被分配到公网IP。公网IP在很大程度上除了让…...
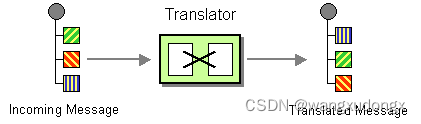
spring integration使用:消息转换器
系列文章目录 …TODO spring integration开篇:说明 …TODO spring integration使用:消息路由 spring integration使用:消息转换器 spring integration使用:消息转换器系列文章目录前言消息转换器(或者叫翻译器&#x…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
