数据结构入门5-2(数和二叉树)
目录
注:
树的存储结构
1. 双亲表示法
2. 孩子表示法
3. 重要:孩子兄弟法(二叉树表示法)
森林与二叉树的转换
树和森林的遍历
1. 树的遍历
2. 森林的遍历
哈夫曼树及其应用
基本概念
哈夫曼树的构造算法
1. 构造过程
2. 算法实现
哈夫曼编码
算法实现
文件的编码和译码
二叉树的运用 - 利用二叉树求解表达式
中缀表达式树的创建
中缀表达式树的求值
注:
本笔记参考:《数据结构(C语言版)》
接下来是树的表示、遍历操作及树林与二叉树之间的对应关系。
树的存储结构
1. 双亲表示法
用一组连续的存储单元存储树的结点,每个结点包括两个域:
![]()
例如:

- 优点:求结点的双亲和树的根会十分方便;
- 缺点:求结点的孩子时需要遍历整个结构。
------
2. 孩子表示法
由于每个结点可以有多棵子树,所以每个结点可以有多个指针域,每个指针域分别指向其中一棵子树的根结点:
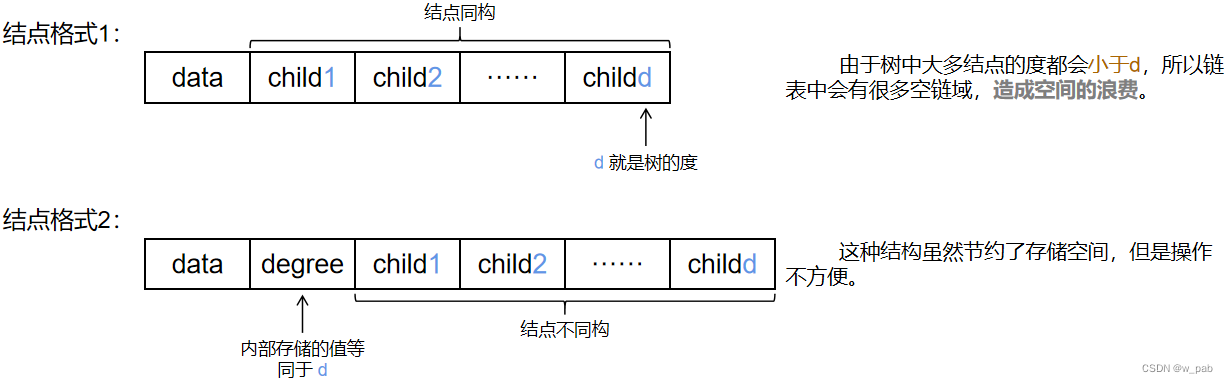
除此之外,还有一种存储结构:在这种存储结构中,由孩子结点组成了一个个线性表,并且把这些链表的头结点再组成一个线性表。
【例如】
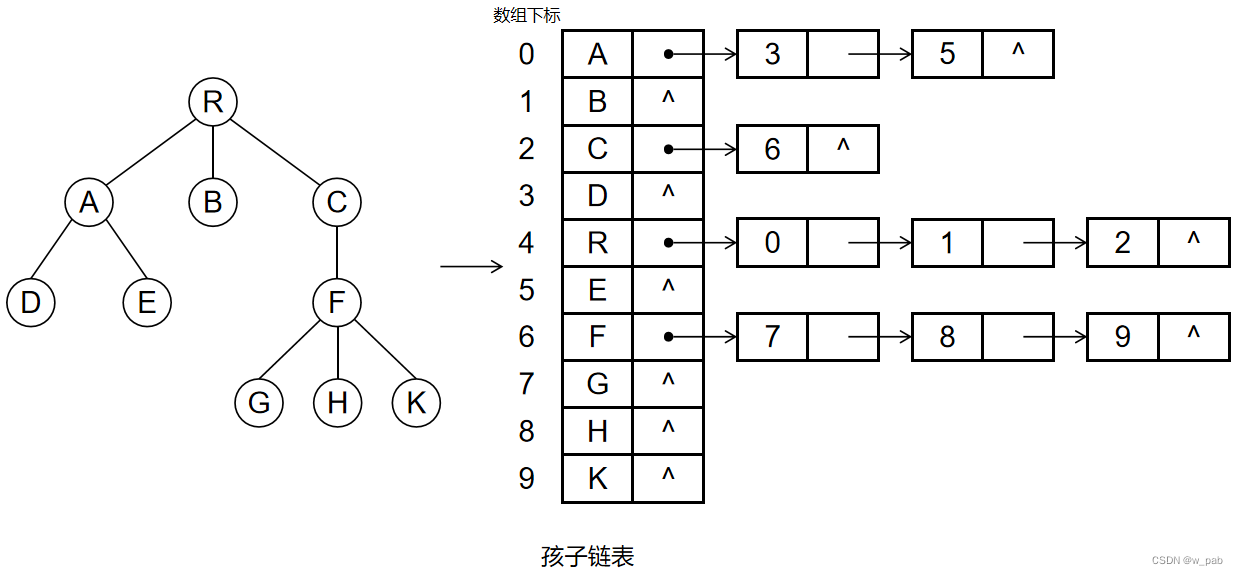
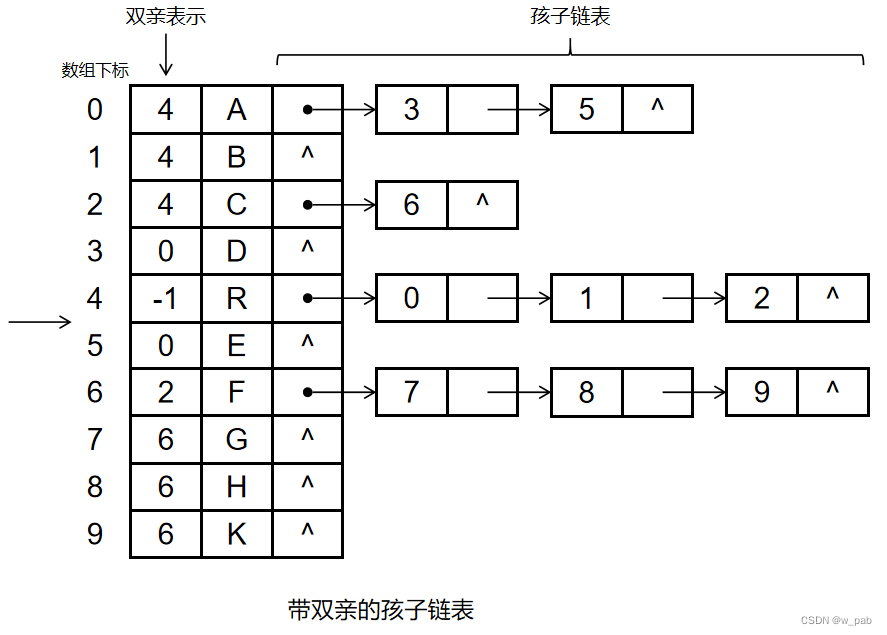
而如果把双亲表示法和孩子表示法结合起来,就会得到又一种存储结构:
------
3. 重要:孩子兄弟法(二叉树表示法)
即将二叉链表作为树的存储结构,这种链表有两个链域:
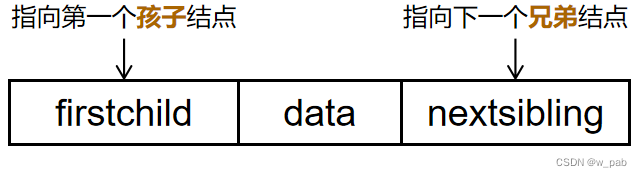
typedef struct CSNode {ElemType data;CSNode* firstchild, * nextsibling;
}CSNode, *CSTree;这种存储结构便于各种关于树的操作,譬如访问孩子节点:只需交替寻找 firstchild域 和 nextsibling域 即可。

而如果要方便寻找双亲结点,仅需在结构上多设置一个 parent域 即可。
如上图所示,这种存储结构与二叉链表完全一致,可以通过这种结构,将一般的树转换成二叉树进行处理。因此,孩子兄弟表示法的运用较为普遍。
森林与二叉树的转换
由上述的孩子兄弟表示法可知,任何一棵和树对应的二叉树,其根结点的右子树必空。例如:
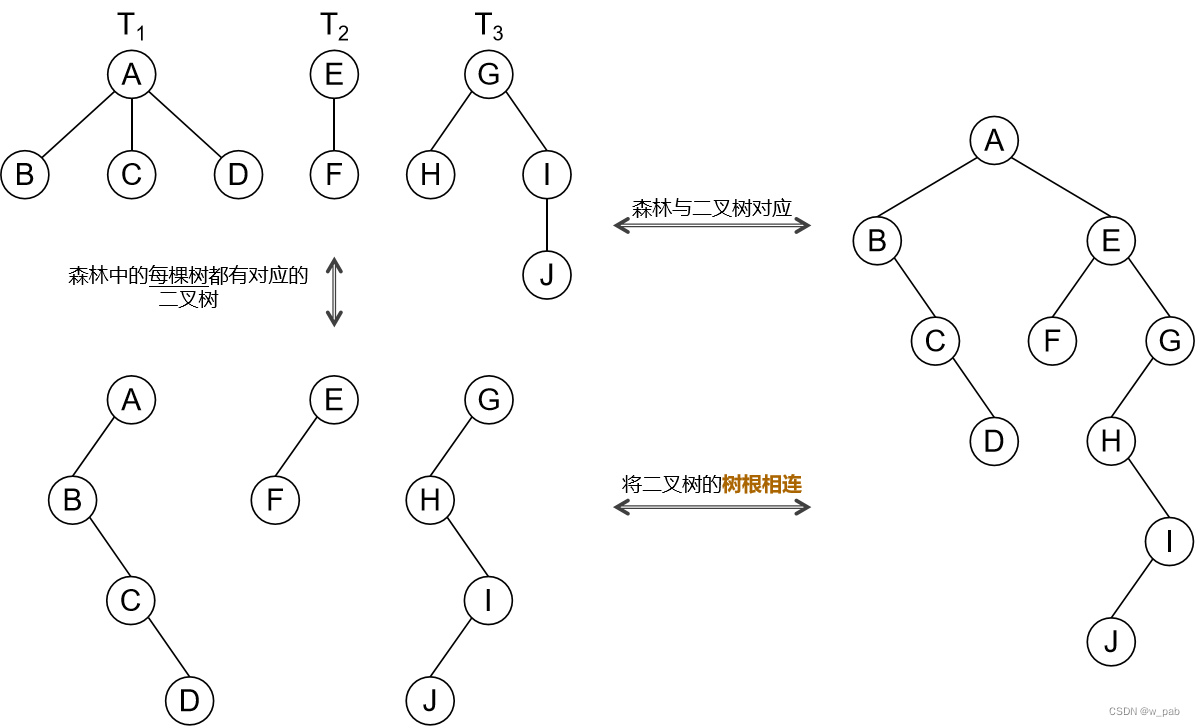
通过上述的例子,就可以揭示森林与二叉树之间的转换规律。
现在假设:
![]()
因为空树就是空二叉树,所以这种情况不做说明。
1. 森林转换为二叉树

2. 二叉树转换为森林

上述所描述的转换方式都可以通过递归实现。
树和森林的遍历
1. 树的遍历
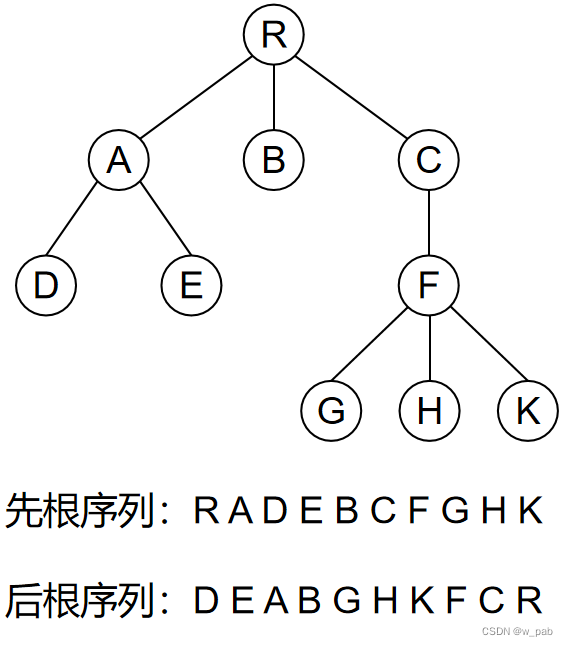
与二叉树不同,树的遍历只有两种方式:
- 先根(次序)遍历:优先访问树的根结点,然后依此访问子树;
- 后根(次序)遍历:先后根遍历子树,再访问对应根结点。
【例如】
2. 森林的遍历
||| 森林和树之间是可以进行相互递归的。
遍历的一个前提:森林非空。
(1)先序遍历规则:
- 访问森林中第一棵树的根结点;
- 先序访问第一棵树的根结点的子树森林;
- 先序遍历由剩余的树构成的森林。
(2)中序遍历规则:
- 中序遍历森林中第一棵树的根结点的子树森林;
- 访问第一棵树的根结点;
- 中序遍历由剩余的树构成的森林。
【例如】
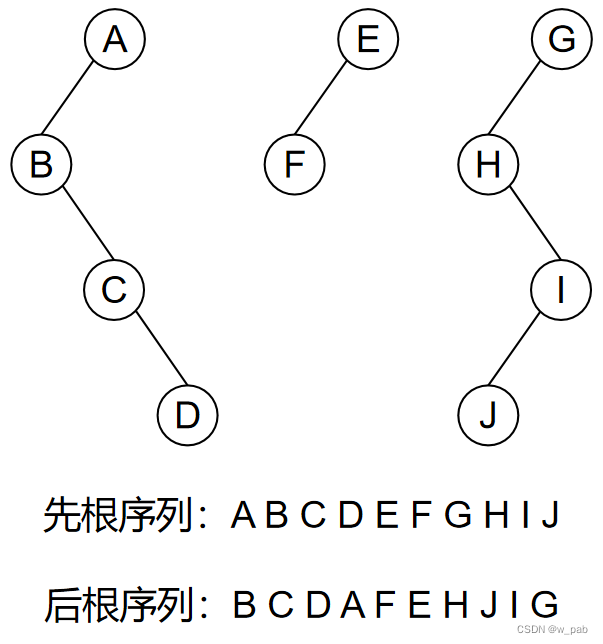
注:此处森林的先序和中序遍历,分别与对应二叉树的先序和中序遍历相对。
哈夫曼树及其应用
基本概念
||| 哈夫曼树(即最优二叉树):是一类带权路径长度最短的二叉树。
以下是一些会用到的概念:
| 概念 | 定义 |
| 路径 | 从树中的一个结点到另一个结点之间的 分支 构成两结点之间的路径 |
| 路径长度 | 即路径上的分支数目 |
| 树的路径长度 | 从树根到每一结点的路径长度之和 |
| 权 | 赋予某个实体的一个量 (是对实体的某个或某些属性的数值化描述) |
| 结点的带权路径长度 | = 该结点到树根之间的路径长度 × 结点上的权 |
| 树的带权路径长度(WSL) | = 树中 所有叶子结点 的带权路径长度之和 |
【例如】
有4个叶子结点a、b、c、d,分别带权7、5、2、4,这4个叶子结点存在于不同的二叉树上:
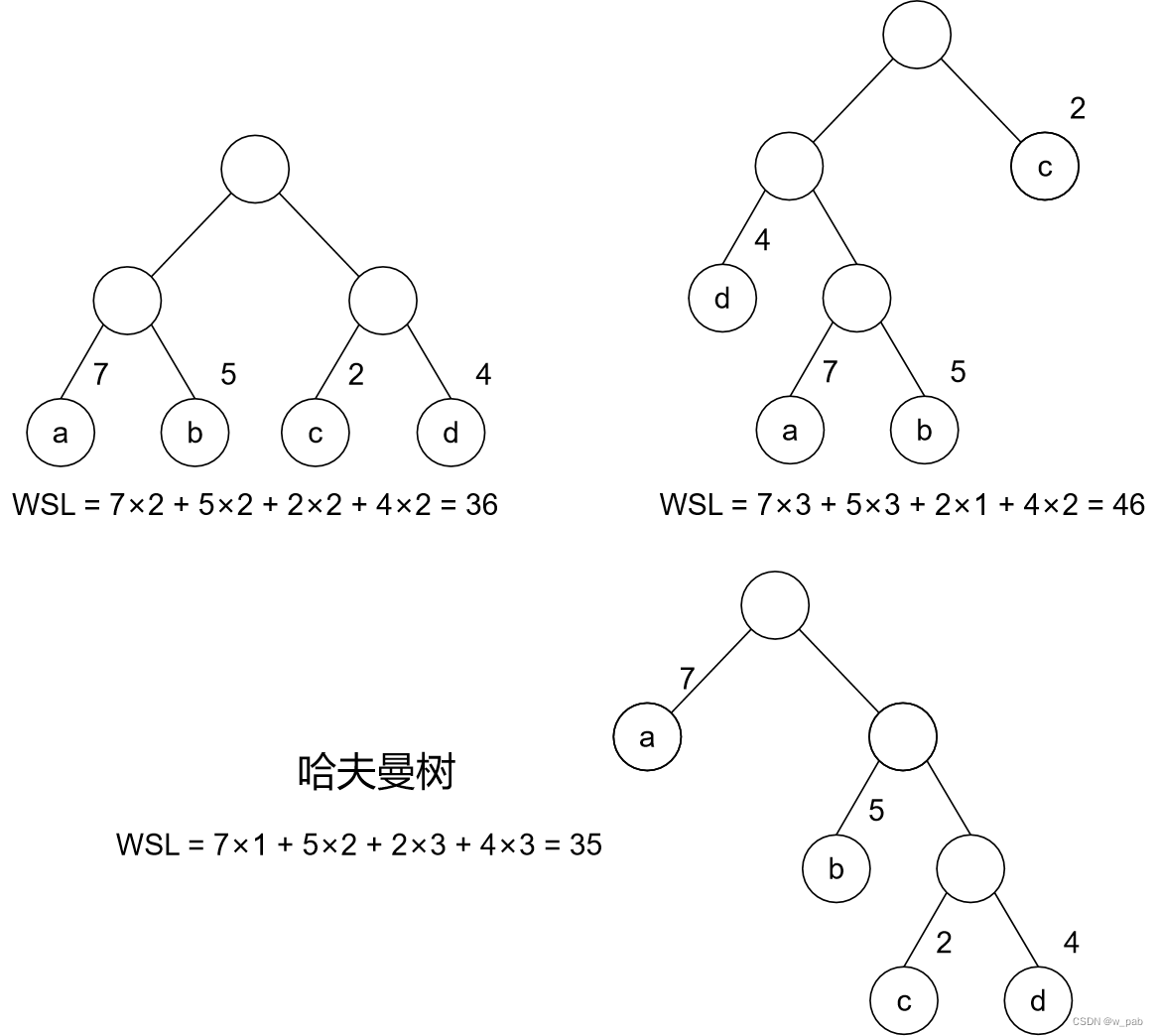
可以验证,下面的这棵树的带权路径长度恰好是最小的(或者说,在所有带权为7、5、2、4的4个叶子结点的二叉树中其值最小),它就是哈夫曼树。
由上述例子可以看出:在哈夫曼树中,权值越大的结点离根结点越近。
哈夫曼树的构造算法
1. 构造过程
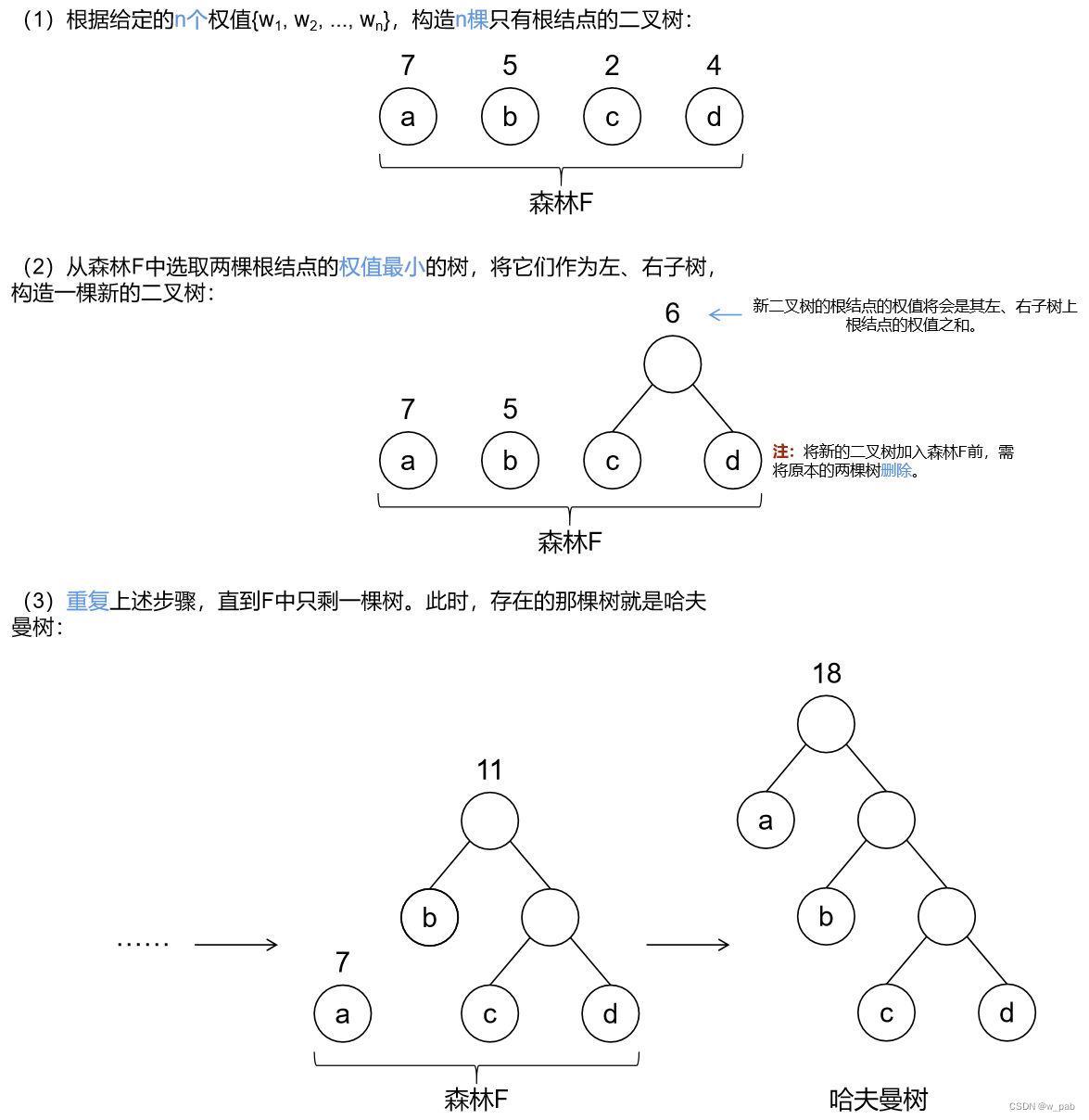
2. 算法实现
由上述构造可知,哈夫曼树中不存在度为1的结点。故若哈夫曼树存在n个叶子结点,则其总结点数一定是2n - 1。
哈夫曼树的结点存储结构:

若将上述的存储结构转换为代码,就是:
typedef struct
{int weight; //结点的权值int parent, lchild, rchild; //结点的双亲、左孩子和右孩子的下标
}HTNode, *HuffmanTree;注意:和以往的链式存储不同,此次是通过动态分配的方式对哈夫曼树进行存储。
在具体的实现中,为了方便,往往会将下标为0的单元置空,所以开辟的数组大小将会是2n。对存储内容进行分类:
- 前1~n个单元:存储叶子结点;
- 后n - 1个单元:存储非叶子结点。
【参考代码:构造哈夫曼树】
void CreateHuffmanTree(HuffmanTree& HT, int n)
{//---初始化开始---if (n <= 1)return;int m = 2 * n - 1;HT = new HTNode[m + 1]; //规定:HT[m]表示根结点for (int i = 1; i <= m; i++){ //处理 1 至 m 个单元(初始化)HT[i].parent = 0;HT[i].lchild = 0;HT[i].rchild = 0;}for (int i = 1; i <= n; i++){ //输入叶子结点的权值(即前n个结点)cin >> HT[i].weight;}//---初始化完毕,开始创建哈夫曼树---for (int i = n + 1; i <= m; i++){ //进行n-1次的构造操作int s1 = 0;int s2 = 0;SelectLeaves(HT, i - 1, s1, s2);//挑选目标结点HT[s1].parent = i; //更改双亲域(相当于删除s1和s2,得到了新结点i)HT[s2].parent = i;HT[i].lchild = s1; //将s1和s2作为i的孩子HT[i].rchild = s2;HT[i].weight = HT[s1].weight + HT[s2].weight;}
}
其中,函数SelectLeaves的参考如下(仅供参考):
//挑选要求: //1. 双亲域为0; //2. 权值最小。 void SelectLeaves(HuffmanTree HT, int i, int& s1, int& s2) {int left = 1;int right = i;while (left < right){if (HT[left].parent == 0 && HT[right].parent == 0){if (HT[left].weight <= HT[right].weight)right--;elseleft++;}else if (HT[left].parent != 0)left++;elseright--;}s1 = left;HT[s1].parent = 1;left = 1;right = i;while (left < right){if (HT[left].parent == 0 && HT[right].parent == 0){if (HT[left].weight <= HT[right].weight)right--;elseleft++;}else if (HT[left].parent != 0)left++;elseright--;}s2 = left; }
哈夫曼编码
为了对数据文件进行尽可能的压缩,有人提出了不定长编码的概念:为出现次数较多的字符编以较短的代码。而通过哈夫曼树设计的二进制编码,就可以满足这一需求。

在上图中,约定:
- 左分支标记为0;
- 右分支标记为1。
由此,根结点到每个叶子结点的路径上的0、1序列就构成了相应字符的编码。这种由各分支的赋值构成的二进制串,就是哈夫曼编码。
前缀编码的概念(提及):若在一个编码方案中,任一编码都不是其他任何编码的前缀(最左子串),则称该编码为前缀编码。譬如:
前缀编码: 0, 10, 110, 111
非前缀编码:0, 01, 010, 111
哈夫曼编码的两个性质:
- 哈夫曼编码是前缀编码(因为路径的不同);
- 哈夫曼编码是最优前缀编码:对于包含n个字符的数据文件,分别以字符的出现次数为权值构造哈夫曼树,再用该树对应的哈夫曼编码压缩文件,可使文件压缩后对应的二进制文件长度最短。
算法实现
主要思想:
- 从叶子出发,向上回溯至根结点。
- 回溯时,走左分支则生成代码0。
- 回溯时,走右分支则生成代码1。
使用一个指针数组作为哈夫曼编码表,存放每个字符编码串的首地址(依旧是从1号单元开始使用):
typedef char** HuffmanCode; //通过动态分配数组存储哈夫曼表在动态开辟数组时,会发现:由于当前并不清楚每个字符编码的长度,所以不能为每个字符分配合适的存储空间。为了解决这个麻烦,通常会动态分配一个长度为n的一维数组作为临时的存储。
注意:由于求解编码的过程是向上回溯的,所以对于每个字符,得到的编码顺序是从右往左的。因此,在将编码往临时的一维数组cd内存储时,顺序也是从后向前的(即字符的第一个编码应该存储到 cd[n - 2] 中,以此类推)。
【参考代码】
void CreateHuffmanCode(HuffmanTree HT, HuffmanCode& HC, int n)
{//将从叶子到根结点回溯求得的每个字符的哈夫曼编码,存储到编码表HC中HC = new char* [n + 1]; //分配存储n个字符编码的编码表空间char* cd = new char[n]; //分配临时存放每个字符编码的动态存储空间cd[n - 1] = '\0'; //编码结束符for (int i = 1; i <= n; i++) //逐字符求编码{int start = n - 1; //从后往前写入int c = i; //从每个叶子结点开始int f = HT[i].parent;while (f != 0) //直到回到根结点为止{--start;if (HT[f].lchild == c) //左、右分支对应不同的代码cd[start] = '0';elsecd[start] = '1';c = f; //继续回溯f = HT[f].parent;}HC[i] = new char[n - start]; //分配空间strcpy(HC[i], &cd[start]); //将求得的编码复制到HC中}delete[] cd;
}【例子】
设在一系统通信内只可能出现8种字符,出现概率分别为0.05,0.29,0.07,0.08,0.14,0.23,0.03,0.11。
为设计哈夫曼编码,将概率作为对应字符的权值,得到:w = (5, 29, 7, 8, 14, 23, 3, 11)。其对应的哈夫曼表为:
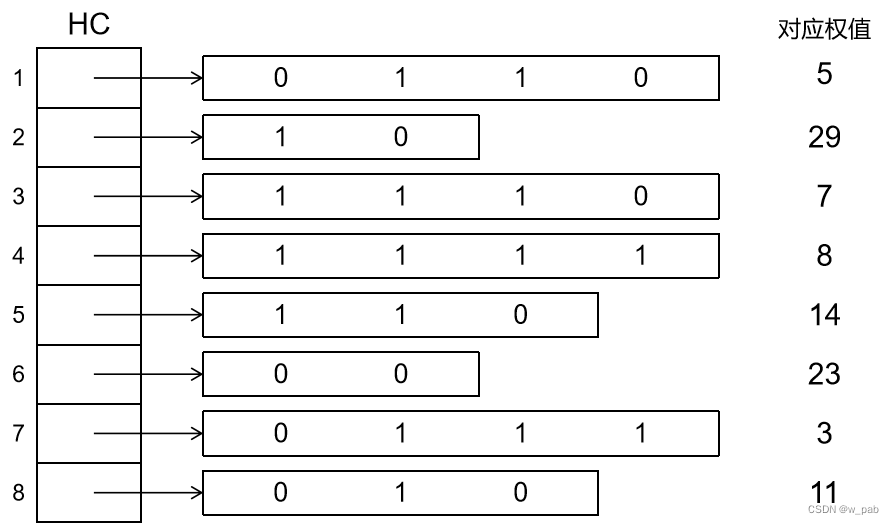
文件的编码和译码
在完成字符集的哈夫曼编码表后,就可以进行编码和译码的操作。
对数据文件进行编码的过程是:
- 依此读入文件中的字符;
- 在哈夫曼编码表HC中找到此字符;
- 将对应字符转换为编码表中存放的编码串。
对编码后的文件进行译码的过程是:
- 依此读入文件中的二进制码;
- 从哈夫曼树的根结点(即HT[m])出发,读入0,则进左孩子;读入1,则进右孩子。一旦到达某一叶子HT[i],则译出相应的字符编码HC[i];
- 循环上述步骤,直到文件结束。
二叉树的运用 - 利用二叉树求解表达式
对于任一算术表达式,都可以使用二叉树进行表示。而当对应二叉树创建完毕时,就可以利用对于二叉树的操作,进行表达式的求值运算。
中缀表达式树的创建
假设:运算符均为双目运算符。
由于创建的表达式树需要准确表达运算的次序,所以需要考虑各个运算符之间的优先级。为此,可以借助一个运算符栈,来存储未处理的运算符。
由两个操作数与一个运算符即可建立一棵表达式二叉树,而该二叉树又可以是另一棵树的子树。可以结组一个表达式树栈,以此来暂存已建立好的树。
【参考代码】
假设每个表达式的开头和结尾均为“#”。
两个工作栈:
- OPTR,用来暂存运算符。
- EXPT,用来暂存已建立好的表达式树的根结点。
【参考代码】
BiTree InitExpTree()
{SqStack EXPT;LinkStack OPTR;InitStack(EXPT); //初始化栈InitLinkStack(OPTR);LinkPush(OPTR, '#'); //将表达式起始符‘#’压入栈顶char ch = 0;cin >> ch;while (ch != '#' || LinkGetTop(OPTR) != '#') //表达式未扫描完毕 || OPTR栈顶元素不是‘#’{if (!In(ch)) //ch不是运算符{BiTree T = new BiTNode;CreateExpTree(T, NULL, NULL, ch); //以ch为根创建一棵只有根结点的二叉树Push(EXPT, T); //将二叉树根结点T压入EXPT栈内cin >> ch;}else{switch (Precede(LinkGetTop(OPTR), ch)) //比较二者的优先级{case '<':{LinkPush(OPTR, ch); //当前字符入栈cin >> ch;break;}case '>':{char theta = 0;BiTree T = new BiTNode;BiTree a = new BiTNode;BiTree b = new BiTNode;LinkPop(OPTR, theta); //弹出OPTR栈顶的运算符Pop(EXPT, b); //弹出EXPT栈顶的两个运算数Pop(EXPT, a);CreateExpTree(T, a, b, theta); //创建新的子树Push(EXPT, T);break;}case '=': //仅当:OPTR栈顶元素是'(',字符ch是')'{char x = 0;LinkPop(OPTR, x);cin >> ch;break;}}}}BiTree T = new BiTNode;Pop(EXPT, T);return T;
}由于字符的限制,上述算法只能进行10以内的运算。
【算法分析】
- 时间复杂度:遍历表达式中的每个字符,故时间复杂度为O(n);
- 空间复杂度:算法运行时所占用的辅助空间主要有OPTR栈和EXPT栈,它们的大小之和不会超过n,故空间复杂度为O(n)。
中缀表达式树的求值
【参考代码】
int EvaluateExpTree(BiTree T)
{int lvalue = 0, rvalue = 0; ///初始值均为0if (T->rchild == NULL && T->lchild == NULL)return T->data - '0'; //若当前结点为操作数,则返回该结点的对应数值else //若结点为操作符{lvalue = EvaluateExpTree(T->lchild);rvalue = EvaluateExpTree(T->rchild);return GetValue(T->data, lvalue, rvalue); //对取得的两个操作数进行计算}
}其中,函数GetValue就是对加、减、乘、除四种运算进行处理的函数。
该算法的时间复杂度和空间复杂度均为O(n)。
相关文章:

数据结构入门5-2(数和二叉树)
目录 注: 树的存储结构 1. 双亲表示法 2. 孩子表示法 3. 重要:孩子兄弟法(二叉树表示法) 森林与二叉树的转换 树和森林的遍历 1. 树的遍历 2. 森林的遍历 哈夫曼树及其应用 基本概念 哈夫曼树的构造算法 1. 构造过程 …...

把Redis当作队列来用,到底合适吗?
文章目录 前言从最简单的开始:List 队列发布/订阅模型:Pub/Sub趋于成熟的队列:Stream1) Stream 是否支持「阻塞式」拉取消息?2) Stream 是否支持发布 / 订阅模式?3) 消息处理时异常,Stream 能否保证消息不丢失,重新消费?4) Stream 数据会写入到 RDB 和 AOF 做持久化吗?…...

Python学习-----项目设计1.0(设计思维和ATM环境搭建)
目录 前言: 项目开发流程 MVC设计模式 什么是MVC设计模式? ATM项目要求 ATM项目的环境搭建 前言: 我个人学习Python大概也有一个月了,在这一个月中我发布了许多关于Python的文章,建立了一个Python学习起步的专栏…...
python网络爬虫(理论+实战)——爬虫实战:指定关键词的百度新闻爬取)
(九)python网络爬虫(理论+实战)——爬虫实战:指定关键词的百度新闻爬取
系列文章目录 (1)python网络爬虫—快速入门(理论+实战)(一) (2)python网络爬虫—快速入门(理论+实战)(二) (3) python网络爬虫—快速入门(理论+实战)(三) (4)python网络爬虫—快速入门(理论+实战)(四) (5)...
数据分析面试、笔试题汇总+解析(六)
(接上篇) 面试题(MySQL篇) 3. 如何提高MySQL的查询速度? 考点解析: 考察面试者对MySQL查询优化的理解 参考答案: (因为这个问题如果回答的详细一点可以写上一整篇,…...

vue3+rust个人博客建站日记3-编写主页
内容 绘制了主页的基本布局设置了封装了header栏组件并设置了全局黑夜模式. 选择一个组件库-Naive UI 如果没有设计能力,又想开发出风格统一的前端页面。就一定要选择一个漂亮的组件库。 本次项目选择使用Naive UI,NaivUI库曾被Vue框架作者尤雨溪推荐…...
前端常考react面试题(持续更新中)
react diff 算法 我们知道React会维护两个虚拟DOM,那么是如何来比较,如何来判断,做出最优的解呢?这就用到了diff算法 diff算法的作用 计算出Virtual DOM中真正变化的部分,并只针对该部分进行原生DOM操作,而…...

C++11多线程编程 二:多线程通信,同步,锁
C11多线程编程 一:多线程概述 C11多线程编程 二:多线程通信,同步,锁 C11多线程编程 三:锁资源管理和条件变量 2.1 多线程的状态及其切换流程分析 线程状态说明: 初始化(Init)&am…...
js——原型和原型链
最近看了很多面试题,看到这个js原型是常考点,于是,我总结了一些该方面的知识点分享给大家,其实原型就是那么一回事,搞明白了就没啥了。结果如下图所示:原型原型又可分为显式原型和隐式原型1.1显式原型显式原…...
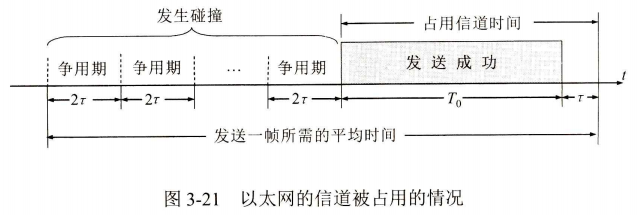
[计算机网络(第八版)]第三章 数据链路层(学习笔记)
物理层解决了相邻节点透明传输比特的问题 3.1 数据链路层的几个共同问题 3.1.1 数据链路和帧 链路: 从一个节点到相邻节点的一段物理线路,中间没有任何其他的交换节点 数据链路: 节点间的逻辑通道是把实现控制数据传输的协议的硬件和软件加…...

void在不同场景下的意义
指针一般有三种含义:一是指明数据的位置,体现在指针的值,表示一个地址。二是表示数据类型的大小,例如int指针表示四个字节为一组数据,体现在指针的加减法如何计算。三是表示数据如何被解释,例如float指针和…...

Flume简介
Flume是一个高可用,高可靠,分布式的海量日志采集、聚合和传输的系统,能够有效的收集、聚合、移动大量的日志数据。 优点: 使用Flume采集数据不需要写一行代码,注意是一行代码都不需要,只需要在配置文件中…...
java简单学习
Java 基础语法 一个 Java 程序可以认为是一系列对象的集合,而这些对象通过调用彼此的方法来协同工作。下面简要介绍下类、对象、方法和实例变量的概念。 对象:对象是类的一个实例,有状态和行为。例如,一条狗是一个对象ÿ…...
Vue2 组件基础使用、父子组件之间的传值
一、什么是组件如画红框的这些区域都是由vue里的各种组件组成、提高复用信通常一个应用会以一棵嵌套的组件树的形式来组织:例如,你可能会有页头、侧边栏、内容区等组件,每个组件又包含了其它的像导航链接、博文之类的组件。为了能在模板中使用…...

代码随想录算法训练营 || 贪心算法 122 55 45
Day28122.买卖股票的最佳时机II力扣题目链接给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。注意:你不能同时参与多笔交易…...
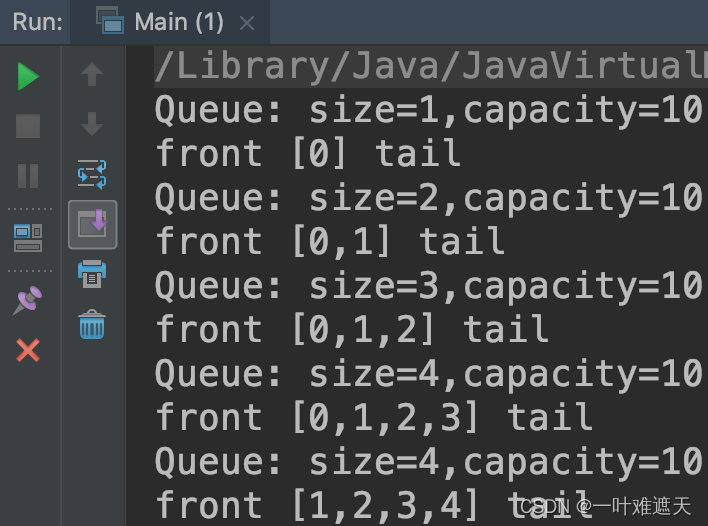
数据结构基础之栈和队列
目录 前言 1、栈 2、队列 2.1、实现队列 2.2、循环队列 前言 上一篇中我们介绍了数据结构基础中的《动态数组》,本篇我们继续来学习两种基本的数据结构——栈和队列。 1、栈 特点:栈也是一种线性结构,相比数组ÿ…...
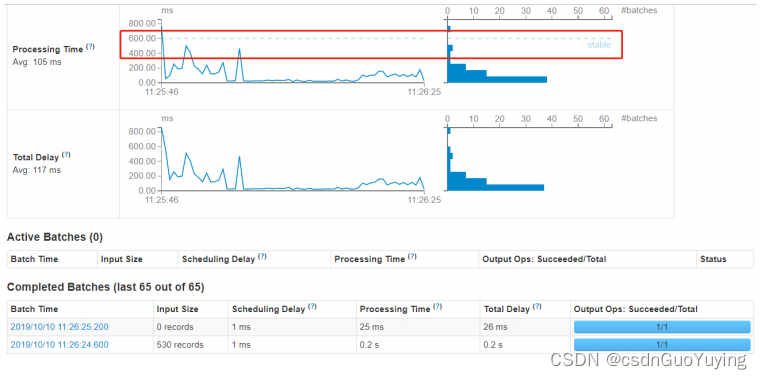
【Spark分布式内存计算框架——Spark Streaming】3.入门案例(上)官方案例运行
2.1 官方案例运行 运行官方提供案例,使用【$SPARK_HOME/bin/run-example】命令运行,效果如下: 具体步骤如下: 第一步、准备数据源启动端口,准备数据 nc -lk 9999 spark spark hive hadoop spark hive 第二步、运行…...

【博学谷学习记录】超强总结,用心分享 | 架构师 Tomcat源码学习总结
文章目录TomcatTomcat功能需求分析Tomcat两个非常重要的功能(身份)Tomcat的架构(设计实现)连接器的设计连接器架构分析核心功能ProtocolHandler 组件1.EndPoint组件EndPoint类结构图2.Processor组件Processor类结构图3.Adapter组件…...
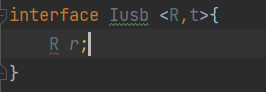
泛型<E>
泛型 案例引出泛型 按要求写出代码: 在ArrayList中添加3个Dog对象,Dog对象有name和age两个属性,且输出name和age public class test1 {public static void main(String[] args) {ArrayList list new ArrayList();list.add(new Dog(10,&quo…...

你对MANIFEST.MF这个文件知道多少?
前言我们在读源码过程中,经常看到每个jar包的METE-INF目录下有个MANIFEST.MF文件,这个文件到底是做什么的呢?在计算机领域中,"manifest" 通常指的是一份清单或概要文件,用于描述一组文件或资源的内容和属性。…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
