刷题小抄1-2数之和
时间复杂度和空间复杂度
对于一个算法高效性的评估,分为时间复杂度与空间复杂度两种,在算法优化到极致的情况下,只能舍弃时间来换取空间,或者舍弃空间来换取时间,故而两者可以说是互斥关系
时间复杂度衡量的是算法运行的速度,而空间复杂度衡量的是算法运行所需要的额外内存空间
在计算机发展初期,计算机的存储容量很小,因此很在乎内存的消耗,也就是更看重空间复杂度,而如今时间复杂度才是决定算法优劣的主要因素
时间复杂度举例
如果存在循环,一般会对循环内使用时间最长(也是运行次数最多的语句进行时间复杂度的估算),例如以下代码中表示n*n矩阵相乘

我们找到最里面的嵌套了三层的循环语句,它被执行了n*n*n次,由于在n很大的时候(时间复杂度计算通常都默认考虑n为大数),执行该句的次数要远远大于其他语句,所以其他语句的执行时间我们都可以忽略,该算法的时间复杂度记为O(n^3)
其他常见的时间复杂度举例:
常数阶O(1):一般发生在没有循环的简单代码中
线性阶O(n):一般发生在一层循环的代码中
平方阶O(n^2): 一般发生在双层循环中
对数阶O(logn):一般发生在二分算法中
ps:
注意并不是有k层循环,时间复杂度就是O(n^k),主要还是得分析运行次数最多的语句和n之间的关系
空间复杂度举例
空间复杂度比较简单,假如对于一个有n个数的数组,你的算法使用常数个变量就能解决问题,那么你的空间复杂度为常数阶O(1),假如你需要额外使用一个同样长度为n的数组或容器来解决该问题,那么你的空间复杂度就为O(n)
两数之和
题目链接
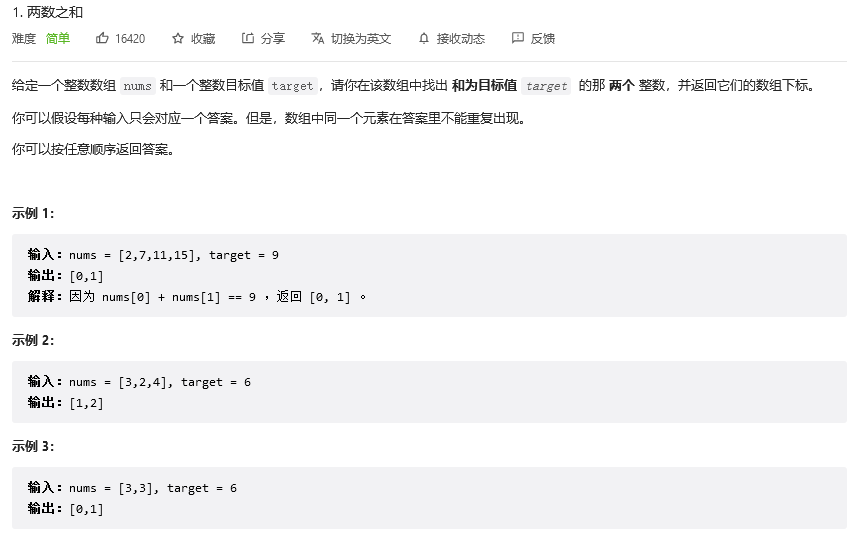

解法一: 双重循环遍历
这是最容易想到的一种解法,通过双重循环不停将两个数字组合,直到找到target,如果使用该解法我们只需要i,j两个指针辅助我们进行遍历,时间复杂度为常数故而为O(1)
对于最坏的情况下,我们在双重循环的末尾才能找到目标,也就是数组中任意两个数都要匹配一次,所以时间复杂度为O(N^2),其中N表示的是元素的数量
class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:n = len(nums)for i in range(n):for j in range(i + 1, n):if nums[i] + nums[j] == target:return [i, j]return []
对于数组为[1,2,3,4,5]寻找target为7,其i,j搜索的方式如下:
i=1时搜索j=2,3,4,5
i=2时搜索j=3,4,5
在i=2,j=5时找到答案,返回结果,否则返回一个空数组
解法二:使用哈希表存储记录过的值
解法一中时间复杂度较高是因为对于数组[1,2,3,4,5],程序对target-x这个值没有感知,其中x是当前遍历到的数组中的值
已知target为7,当我们在搜索[1,2,3,4,5]这个数组的时候,能不能通过一次遍历,不使用双重循环,在搜索到5的时候感知到我们曾经搜索过2(target-x)数字呢,这里就需要使用额外空间了,只要使用一个容器,记录曾经遍历过的数字,然后在这个容器中寻找是否有target-x即可
初学者可能会有疑问,既然还要在容器中把target-x再找到,那岂不是又要遍历一遍,时间复杂度还是没有下降,没错,正常容器不可以,但是哈希表可以,在python中它的名字是hashtable,进入它的元素,它都能使用O(1)时间复杂度给你查找出来,这是它的强大之处,它的存储形式为(key,value)键值对,加入向hashtable中插入(key,value1)与(key,value2)那么value2的值会覆盖掉value1的值,因此hashtable还有去重的作用
class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:
#初始化哈希表hashtable = dict()for i, num in enumerate(nums):
#如果查找到了target-xif target - num in hashtable:
#返回结果return [hashtable[target - num], i]
#该句中将(nums[i],i)这个数对放入hashtable中hashtable[nums[i]] = ireturn []时间复杂度: O(N),我们只遍历了一遍所有的元素
空间复杂度: O(N),主要是我们使用了哈希表这个额外的容器
课后作业
在两数之和的解法一中,我们使用两个索引,双重循环的方式得到了结果
对于三数之和,我们需要使用三个索引,三重循环,那么我们每次固定其中的一个索引,是否就能转换三数之和问题为两数之和呢,这样的解法是可行的,但是同样存在时间复杂度过高的问题,并且如果考虑全重复元素的极限情况,该方法是不是也不能达到排重的效果呢
假如对于三数之和使用解法二,由于hash表只能解决两数之和的问题(因为只能存储一个数对),那么每次固定最外层的索引就需要一个hash表,对于n很大的时候,空间复杂度是不可估量的,所以也不行
对于三数之和,四数之和这些衍生题型,由于有排重操作,应该使用双指针+排序
- 排序的作用: 将相同的元素聚集在一起,通过考虑当前元素和上一个元素是否一致就能进行排重了,并且在被排序的数组中,指针向左移动,三数之和变小,指针向右移动三数之和变大,结果变得有导向性
- 双指针的作用: 从左右两端开始向里移动,如果相遇则遍历完成,代替了双重循环,简化了时间复杂度
课后作业:三数之和,四数之和
相关文章:

刷题小抄1-2数之和
时间复杂度和空间复杂度 对于一个算法高效性的评估,分为时间复杂度与空间复杂度两种,在算法优化到极致的情况下,只能舍弃时间来换取空间,或者舍弃空间来换取时间,故而两者可以说是互斥关系 时间复杂度衡量的是算法运行的速度,而空间复杂度衡量的是算法运行所需要的额外内存空…...
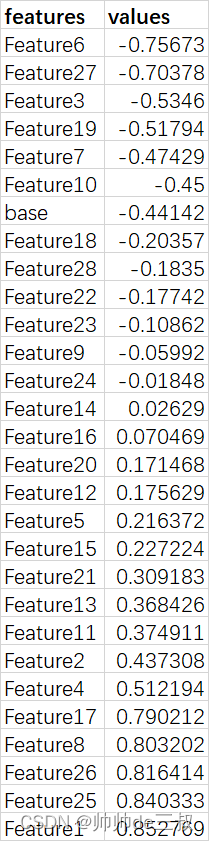
axicom的测试文档
目录)SQLpython开放性业务题(二选一)完整代码SQL 问题描述 SQL, 请根据前一周各产品的总GMV将其分成五类:GMV Top 20%、20%-40%,40%-60%,60%-80%以及Bottom 20%的产品组,请计算这五…...
)
基于vue3异步组件、动态组件、vite批量导入实现路由权限动态管理(非addRoute方案)
开发后台管理系统必备的需求:动态菜单权限管理、或者说路由权限动态管理 原理是通过addRoute实现路由权限控制,一般分为两种: 后端生成当前用户相应的路由后由前端(用 Vue Router 提供的API)addRoutes 动态加载路由前…...

带中转hub的卡车无人机车辆路径问题
本文介绍了两类无人机卡车协同配送问题: 第一类是旅行商问题,也即一辆卡车拉着一架无人机服务给定的节点集合第二类是车辆路径问题,这里强制要求了一架卡车只能搭配一架无人机无人机卡车旅行商问题 符号列表: N N N:表示所有节点集合,含起始和终止节点M M M...
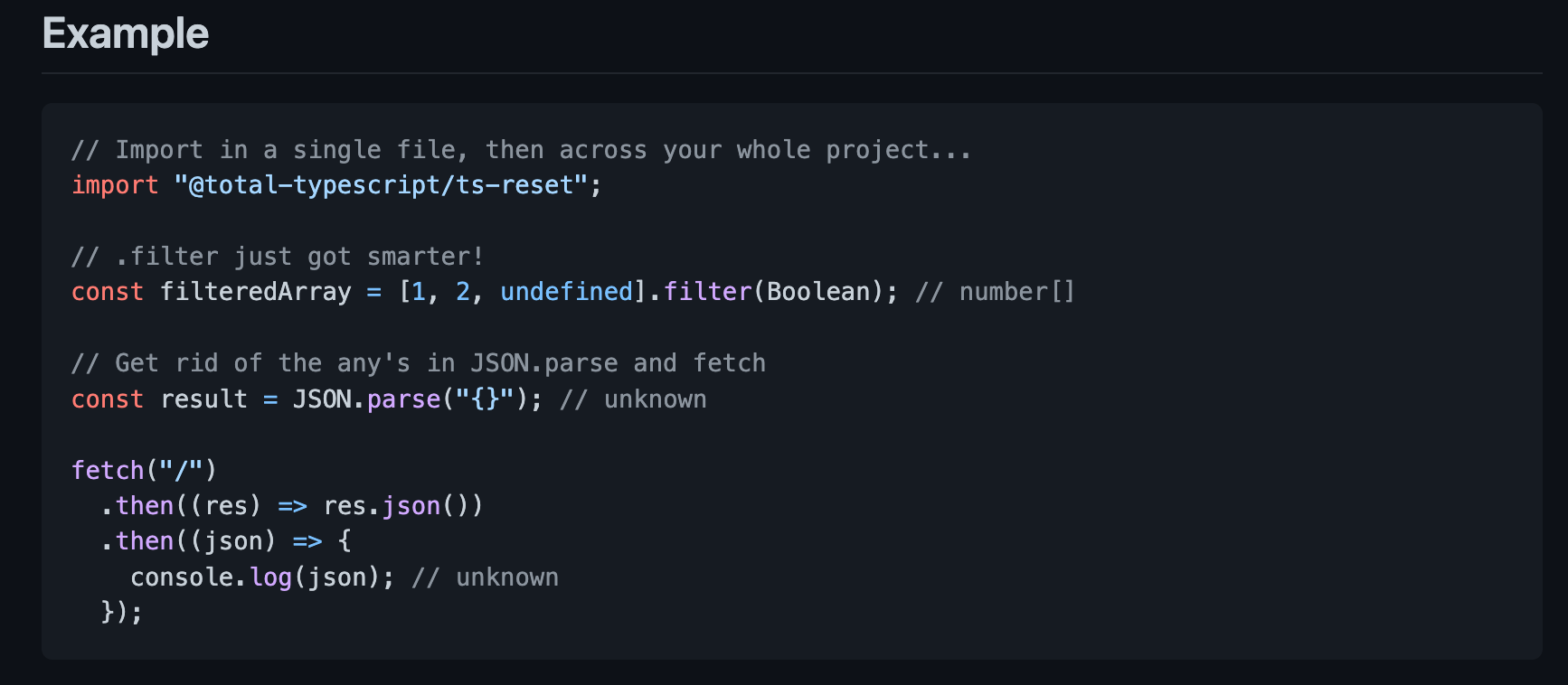
前端食堂技术周刊第 72 期:Signals 是前端框架的未来、Chrome Headless、ts-reset、magic-regexp、Bun 新文档
美味值:🌟🌟🌟🌟🌟 口味:草莓番茄 食堂技术周刊仓库地址:https://github.com/Geekhyt/weekly 本期摘要 Signals 是前端框架的未来Chrome Headless 进化成完全体Next.js 13.2Deno…...

mysql中用逗号隔开的字段作查询用(find_in_set的使用)
mysql中用逗号隔开的字段作查询用(find_in_set的使用) 场景说明 在工作中,经常会遇到一对多的关系。想要在mysql中保存这种关系,一般有两种方式,一种是建立一张中间表,这样一条id就会存在多条记录。或者采用第二种方式ÿ…...
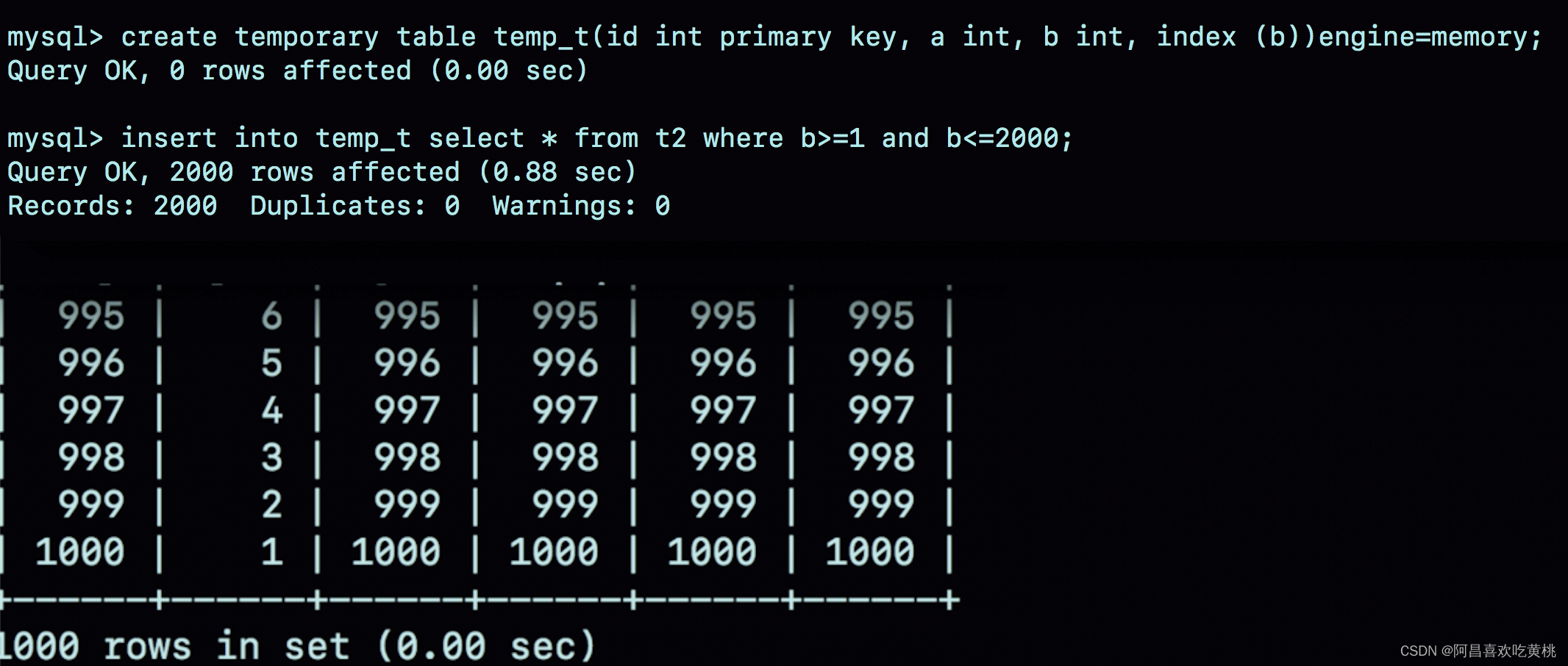
Day902.Memory存储引擎 -MySQL实战
Memory存储引擎 Hi,我是阿昌,今天学习记录的是关于Memory存储引擎的内容。 两个 group by 语句都用了 order by null,为什么使用内存临时表得到的语句结果里,0 这个值在最后一行; 而使用磁盘临时表得到的结果里&…...
Linux(Centos)安装RabbitMQ+延时插件+开机自启动
安装目录1:前言1.1 系统环境1.2:安装版本1.3 简介2:安装2.1:安装前准备:2.2:安装Erlang2.3:安装RabbitMQ2.3:延迟依赖插件安装1:前言 1.1 系统环境 操作系统版本&#…...
)
最近是遇到了CKPT(BLOCKED)
半夜被电话吵醒,数据库不可用了,无法交易。 远程登录查看,这个时候就没有所谓的安全不安全了,都可以远程了。 onstat - 数据库处于CKPT(REQ) CKPT:BLOCKED状态 onstat -l 发现所有的逻辑日志都是U------状态ÿ…...
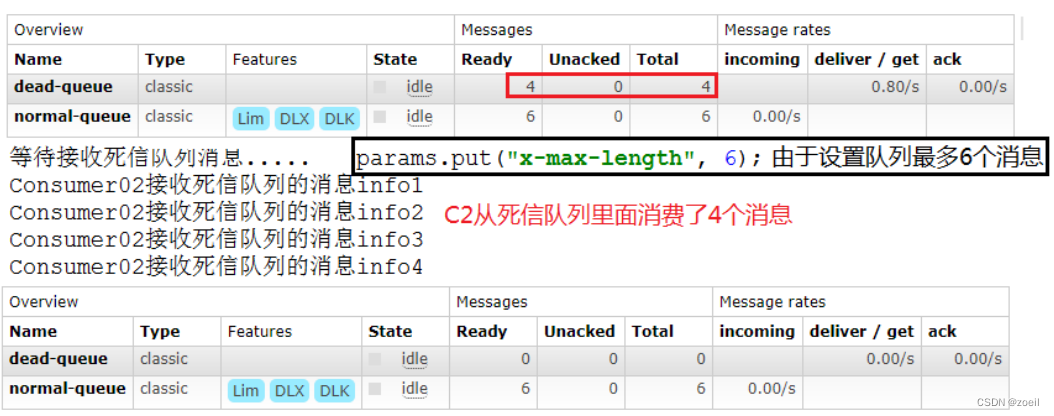
RabbitMQ死信队列
目录 一、概念 二、出现死信的原因 三、实战 (一)代码架构图 (二)消息被拒 (三)消息TTL过期 (四)队列达到最大长度 一、概念 先从概念解释上搞清楚这个定义,死信&…...

Word控件Spire.Doc 【书签】教程(1):在C#/VB.NET:在 Word 中插入书签
Spire.Doc for .NET是一款专门对 Word 文档进行操作的 .NET 类库。在于帮助开发人员无需安装 Microsoft Word情况下,轻松快捷高效地创建、编辑、转换和打印 Microsoft Word 文档。拥有近10年专业开发经验Spire系列办公文档开发工具,专注于创建、编辑、转…...
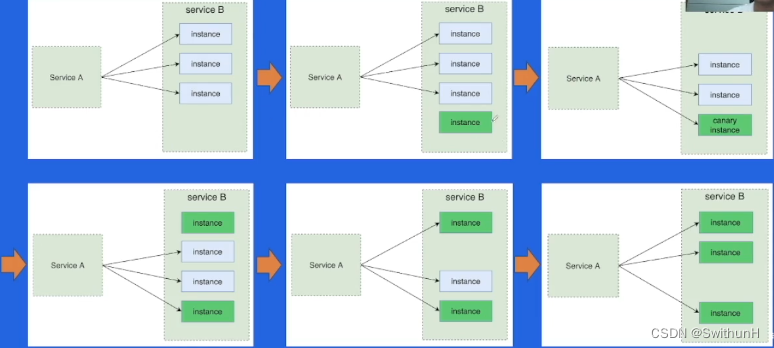
微服务框架-学习笔记
1 微服务架构介绍 1.1 系统架构演变历史 单体架构垂直应用架构:按照业务线垂直划分分布式架构:抽出业务无关的公共模块SOA架构:面向服务微服务架构:彻底的服务化1.2 微服务架构概览 1.3 微服务架构核心要素 服务治理࿱…...

实验心理学笔记01:引论
原视频链接: https://www.bilibili.com/video/BV1Qt41137Kv 目录 一、实验心理学:定义、内容及简要历史回顾 二、实验心理学和普通心理学、认知心理学的区别 三、实验方法与非实验方法 四、实验范式 五、实验中的各种变量 六、The science of psy…...

预备3-如何学习编程
如何学习编程 我说说曾经学习编程踩得坑 纠结字面上的意思 如纠结一个关键词的名称如何来 为什么叫这个名称... 只是一个简单的名称,该名称代表某一想象/行为,就好比你为啥叫张三, 千万别去深究这些...做笔记的时间比敲代码的时间还多 做笔记的原因是,自己总结归纳所学的知识, …...

操作系统权限提升(十七)之绕过UAC提权-Windows令牌概述和令牌窃取攻击
系列文章 操作系统权限提升(十二)之绕过UAC提权-Windows UAC概述 操作系统权限提升(十三)之绕过UAC提权-MSF和CS绕过UAC提权 操作系统权限提升(十四)之绕过UAC提权-基于白名单AutoElevate绕过UAC提权 操作系统权限提升(十五)之绕过UAC提权-基于白名单DLL劫持绕过UAC提权 操作系…...
)
【时间之外】系统管人,能行?(冷眼旁观连载之二)
上次写了在用的工具系统和痛点,基本情况都交待清楚了,春节假期很快就过去了。这次继续按照之前观察计划,谈谈对这些工具使用情况的感受,学而时习之,算是抛砖引玉,也算是个人对这项工作的总结和体会。 目录…...
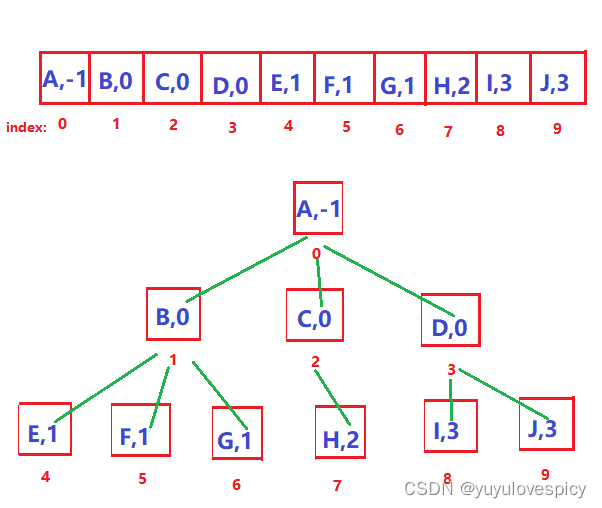
【数据结构必会基础】关于树,你所必须知道的亿些概念
目录 1.什么是树 1.1浅显的理解树 1.2 数据结构中树的概念 2.树的各种结构概念 2.1 节点的度 2.2 根节点/叶节点/分支节点 2.3 父节点/子节点 2.4祖先节点/子孙节点 2.5兄弟节点 2.6树的度 2.7节点的层次 2.8森林 3. 如何用代码表示一棵树 3.1链式结构 3.1.1 树节…...
)
设计模式的应用(已在大型项目中使用)
说明:开发语言:在本文中,使用的是C# 一、目录 •1 、单例模式 •2 、简单工厂模式 •3 、代理模式 •4 、观察者模式 •5 、外观模式 •6 、享元模式 •7 、命令模式 •8 、状态模式 •9 、发布订阅模式...

Git的相关用法
1.全局设置自己的git提交用户名和邮箱git config --global user.name 张三 git config --global user.email zsgmail.com即所有的提交都会用这个姓名和邮箱。如果不知道自己配置的是什么,可以查询下git config --global user.name git config --global user.email 或…...
Linux服务:Nginx反向代理与负载均衡
目录 一、Nginx反向代理 1、什么是代理 2、实现反向代理实验 ①实验拓扑 ②实验目的 ③实验过程 二、反向代理负载均衡 1、反向代理负载均衡调度算法 ①轮询算法 ②加权轮询算法 ③最小连接数算法 ④ip、url 哈希算法 ⑤响应时间fair算法 2、实现反向代理负载均…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...
