【数据结构必会基础】关于树,你所必须知道的亿些概念
目录
1.什么是树
1.1浅显的理解树
1.2 数据结构中树的概念
2.树的各种结构概念
2.1 节点的度
2.2 根节点/叶节点/分支节点
2.3 父节点/子节点
2.4祖先节点/子孙节点
2.5兄弟节点
2.6树的度
2.7节点的层次
2.8森林
3. 如何用代码表示一棵树
3.1链式结构
3.1.1 树节点的定义方式1(指针数组)
3.1.2 树节点的定义方式2(左孩子右兄弟表示法)
3.2数组结构
3.2.1 每个节点存父亲下标
3.2.2 完全二叉树的数组表示法
1.什么是树
1.1浅显的理解树

树,其实就是我们现实中的树(注意看有好多分支),但是现在这棵树是一个数据结构!
在数据结构当中,我们设计结构的目的是为了存储数据,我们所说的树亦是一个能存数据的树。或者更准确的说,是一个一个的数据按照树型结构组织在了一起。那这是一种什么样的数据结构呢?
之前了解到的数据结构,如顺序表,链表等,他们都是线性的存储结构,即一个数据连接着下一个数据,在逻辑上上是呈现线性的。而树这种数据结构则不同,所有数据组织在一起的方式并不是一条单纯的直线了,而是一个树形。
1.2 数据结构中树的概念
树是一种非线性的数据结构,它由一个一个的有限数量的节点组织形成,本质上就是节点的集合。在实际coding当中,一棵树是一个倒挂的树,即root树根是在最上层,叶子在最底层。
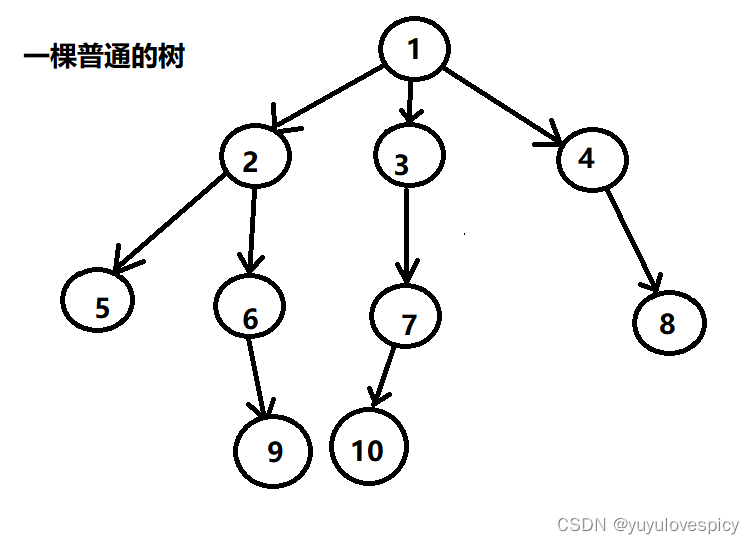
所以实际上我们数据结构中的树是一棵倒挂的树,根在最上面。

树当中,有一个特殊的节点,就是根节点,除了空树,每一棵树都有根节点,根节点是唯一的,根节点之上没有其他的节点。
每一棵树,都可以这样划分:根 根的子树1,子树2,子树3 ........ 子树n(n是看根有多少棵直接子树)。
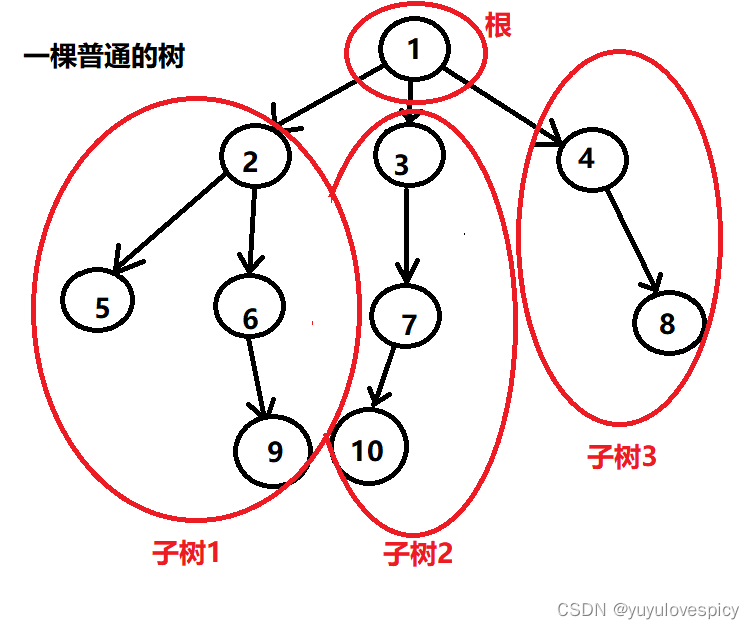
每一棵子树,也都是一棵树。也可以分为子树的根,子树根 的 子树1,子树2......子树n。
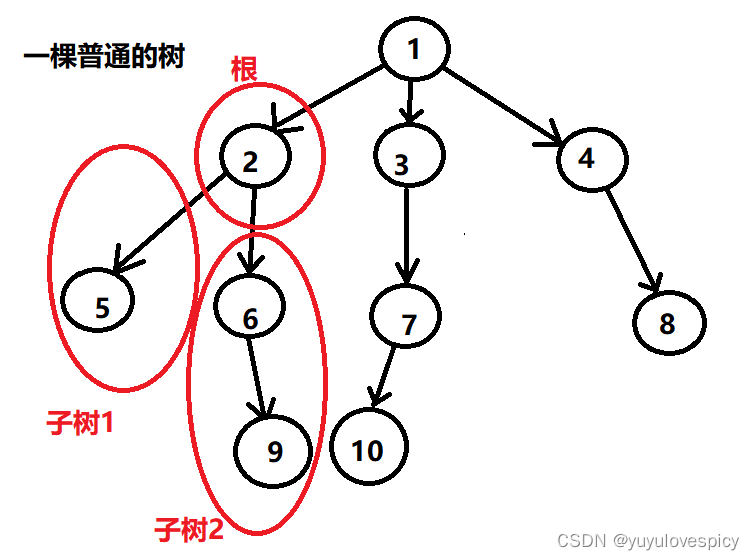
按照这个思路,一棵树由根 + 所有的的每一颗子树,组成划分的;根的每一棵子树,也都是按 根 + 所有的每一颗子树构建的;所有的子树的子树,也都是按 根 + 所有的的每一颗子树 方式组织的;所有的子树的子树的子树(此处省去一万字)。。。。。。
所以树本质上都是通过递归定义的。
2.树的各种结构概念
2.1 节点的度
节点的度,就是一个节点的子树的个数,或者说,就是一个节点有几个分叉。

如上面 1节点,它的度就是3(有3个子树/分叉 2 3 4);2节点,它的度是2(有2个子树/分叉 5 6);7节点,它的度是1(只有一个子树/分叉)。
2.2 根节点/叶节点/分支节点
根节点:就是最开始的一个节点(如图的 1节点),它是唯一的。从根开始找,这棵树的所有节点都可以遍历找到。所以只要找到了一棵树的根,这棵树就算是被我们所“掌控”。

叶子节点:度为0的节点,即往下没有子树/分支的节点。即我这个节点的下面就没有任何东西了(空),我这个节点就是叶子节点。(如图中的 5 9 10 8,是上图中树的叶子节点)。
分支节点:这是叶子节点的对立,即度不为0的节点,只要不是叶子节点,那你就是分支节点。
2.3 父节点/子节点
父节点:就是一个节点的父亲。就是一个节点上面的那一个节点,如在下图当中,5的父节点是2,10的父节点是7,3的父亲节点是1.。
这里需要着重强调:就像在现实当中任何一个人都只有一个爹,任何一个节点,也都只有一个父节点。(除根节点,根节点没有父亲)
要找到任何一个节点,也只能通过父亲节点找到。父节点,也只能由他的唯一的父亲节点找到,所以其实在树中,要找到任何一个节点都只有唯一的一条路径。

相对于父节点,那父的儿子就是子节点,即父亲往下可以直接找到的节点。就像现实当中,一个爹,都可以有多个儿子,也可以有一个儿子,也可能没有儿子,在树当中,任何一个节点,只要在我这个节点的下面能直接找到的节点,那这就是子节点。
如1的子节点,就是2 3 4节点;2的子节点,就是5 6节点;4的子节点,就只有 8节点。
2.4祖先节点/子孙节点
祖先节点:从根到该节点所经分支上的所有节点,都是祖先节点。类比现实,你爹是你的祖先,你爷爷是你的祖先,你太爷爷是你的祖先……你的太太太太太太太爷爷都是你的祖先。(当然这里我们也可以知道,根节点一定是所有节点的祖先节点)
如6节点的祖先节点是2 1节点;如9节点的祖先节点是6 2 1节点;如8节点的祖先是4 1节点。
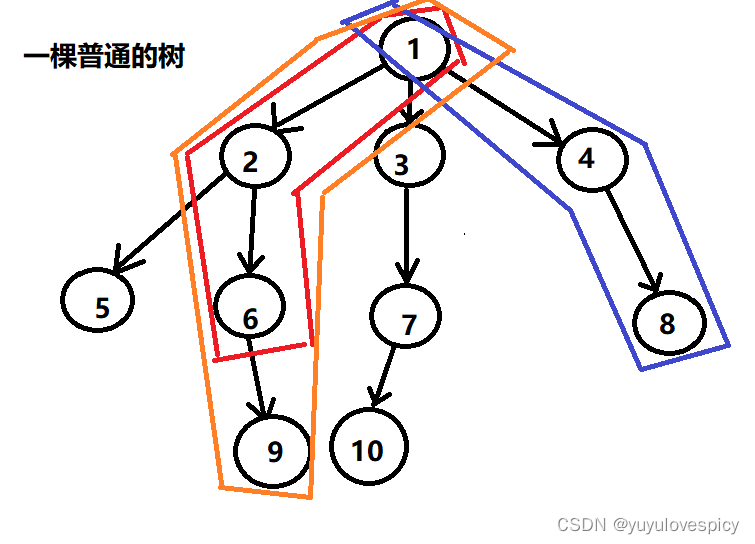
子孙节点:祖先是从根节点找到该节点路径上的所有点,而子孙,其实就是我这个节点能被某个节点所找到!!!即只要,我这个节点只要能往下找到你,我就是祖先,你就是子孙。如2节点作为祖先节点,那5 6 9这三个节点就都是子孙节点。
2.5兄弟节点
兄弟节点:(必须是亲兄弟!!!)有同一个的父节点,我们才是兄弟节点!!!
如下图当中5和6才是兄弟节点,6和7就不是兄弟节点,7和8就不是兄弟节点。

2.6树的度
是一棵树中,所有节点的最大度,称之为树的度。就是所有的节点的度中,挑出其中最大的节点度。PS:最大的节点度,不一定是根节点的度,我们要求的是有最多分支的节点。
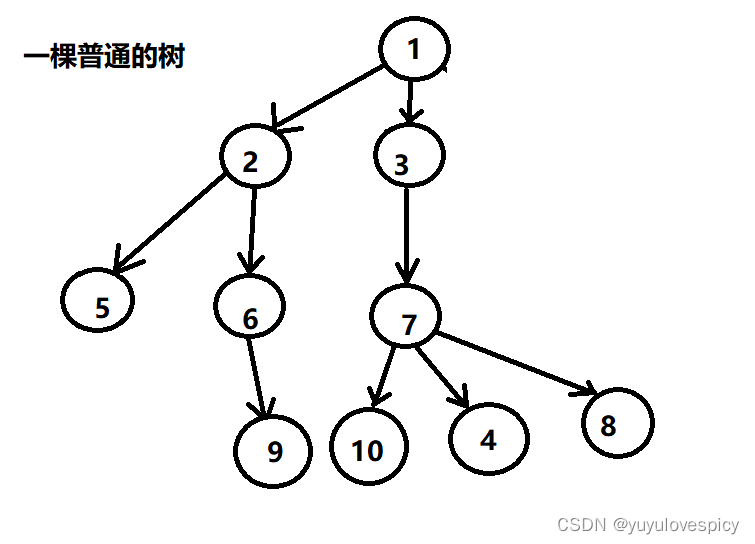
如这棵树,它的度就是3:即7这个节点的度,是所有节点当中度最大的(3,其余节点的度都是2或1或0),所以这棵树的度就是3。
2.7节点的层次
从根开始定义起,根为第1层,根的子节点为第2层。节点的层次也叫树的高度/深度。
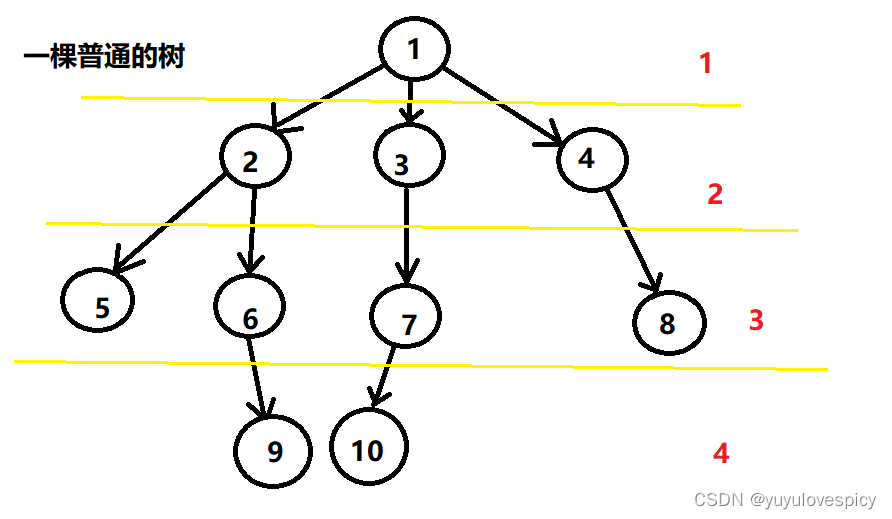
当然也有些地方根是第0层,根的子节点为第1层,即上图分为0 1 2 3层,这样也说的过去。
不过我们还是推荐 1 2 3 4 (如上图画的那样),这样方便理解:
空树是没有根节点,如果我们算根节点为第1层,这样空树的高度我们就可以换定义为0了,更加符合我们的观感!
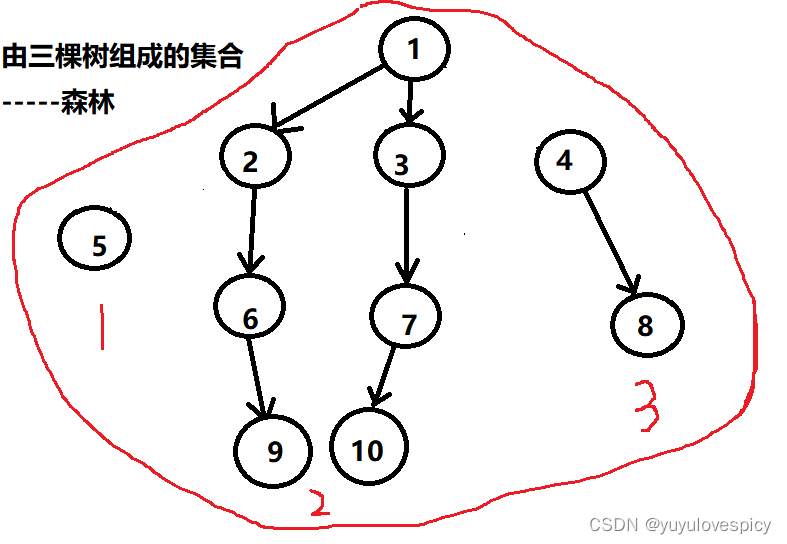
2.8森林
有N(N>0)棵树,即至少一棵 互不相交的树 的集合称为森林。
如并查集这个数据结构就是森林(就是有多棵树嘛)。
3. 如何用代码表示一棵树
刚才我们只是从抽象图上表征了树,那落实到代码当中,一棵树如何用代码来表示呢?我们可以用链式结构来表示一棵树,也可以用数组结构来表示一棵树。
3.1链式结构
要用链式结构来实现树,我们就要首先定义出来一个节点类,因为我们一定是把一个一个的节点链起来组成的一棵树(当然节点与节点之间的链接,我们是通过指针来实现的)。节点是组成树的基础。那如何定义节点类呢?
3.1.1 树节点的定义方式1(指针数组)
我们节点TreeNode要存一个数据data,这个毋庸置疑,然后就是要存储指针,即链接到子节点的链子。那这样就有一个问题,我每个节点的子节点的数量是不一定的,要使用的链子(指针)数量也是不一定的,所以我们要存储多个节点指针。
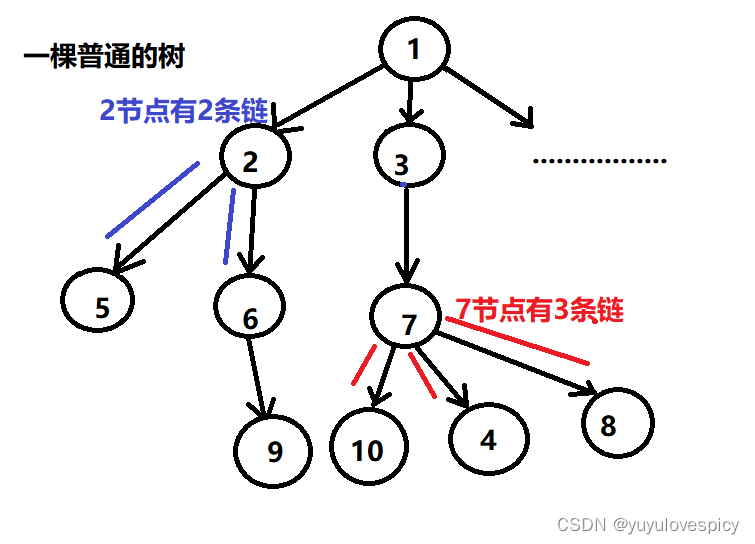
一种方法是让每个节点存储一个指针数组,这个指针数组可以是一个定长的。
struct TreeNode
{int data;struct TreeNode* *pSonNode[N];
};但是这种情况是存在缺陷的,如果你知道了这个树的度(即一个节点,最大所能有的分叉数量),或者你规定这个树是固定有多少个叉的,那这个N是可以确定的,可是如果没有给这个度,那N存多大就很难确定了:如果N给大了,那就会造成很多的空间浪费。如果N给小了,有可能导致有的节点,所能链接到的节点数量受限。
所以我们通常是存一个可以动态增长的数组指针,按需给相应大小数量的指针。
struct TreeNode
{int data;vector<struct TreeNode*> pTreeSon;
};上面的方法,在指定了这是几叉树 / 该树的度确定,这两种情况下,在节点中直接存储指向孩子的指针,这的确是一种很好的表示树的方法。但是现实中,树的情况是很复杂的,对于度不确定的这种树,我们不推崇上面这个方法,我们有一个也是很好的方法---左孩子右兄弟表示法。
3.1.2 树节点的定义方式2(左孩子右兄弟表示法)
struct TreeNode
{int data;struct TreeNode* Left_FirstChild;struct TreeNode* Right_NextBrother;
};每一个节点,只存,链接到 最左的孩子(即我的第一个孩子)的指针,以及链接到 右边的兄弟(即我旁边的那个亲兄弟节点)的指针。
举个例子:如下图,2节点,我只存储两个指针:我的Left_FirstChild为指向最左边的即第一个孩子5,我的Right_NextBrother为指向我右边的即旁边的亲兄弟3。
再如下图的6节点:我的Left_FirstChild,指向的是第一个孩子9。而我Right_NextBrother,旁边右边的第一个亲兄弟,是空!这里注意哦,兄弟指代的是亲兄弟哦!你只能说6和7是堂兄弟的关系。反正我7节点的右边是没有亲兄弟的,所以Right_NextBrother存NULL。
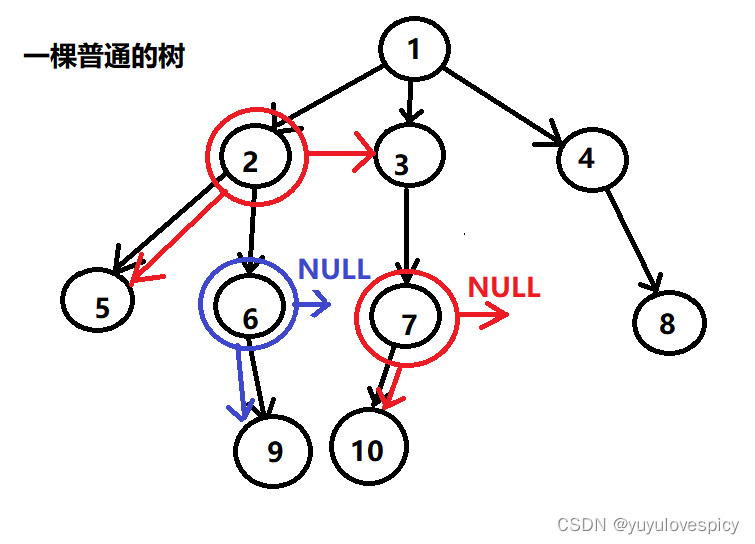
那这样存为什么能够表示整棵树呢? 画个图你就明白了:比如我们要用这个左孩子右兄弟法表示下面这棵树:
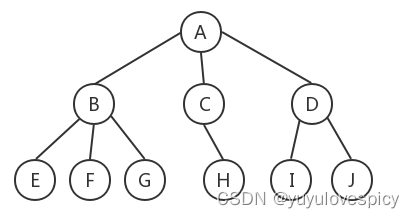
那么如果我们用左孩子右兄弟法,组织节点,组织成这棵树:
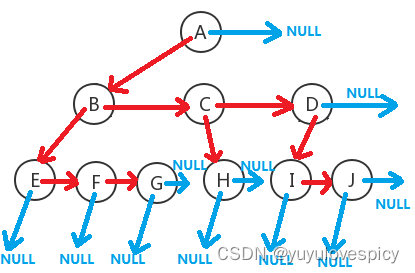
你可以看到,这种方法其实是把每一个节点都建立了被链接关系,即我总是能通过某条路径找到这个节点,我们可以根据左孩子右兄弟法这些安插的链子,找到所有节点。
(只要可以找到/遍历到任何节点,那这就是一种成功的表示树的方法)
例如要找H节点,我们可以通过A的左孩子找到B,然后通过B的右兄弟找到C,然后通过C的左孩子找到H节点;
再例如要找到G节点,我们可以通过A的左孩子找到B,然后通过B的左孩子找到E,然后通过E的右兄弟找到F,然后通过F的右兄弟找到G节点。.
这种方法,相比第一种方法,对于任意树的构建,是没有空间浪费的,而且可以全部遍历找到,非常优!!!
3.2数组结构
没错,我们用一个数组,也可以组织表示一棵树哦!(后面写并查集的时候,一个数组甚至能够表示一个森林,也就是多棵树)是不是很神奇!?下面我们具体看一下如何实现。
3.2.1 每个节点存父亲下标
我们每个节点,即每个节点的数据都存储在一个数组的一个格子当中,这样每一个数据就都有了一个存储下标index,然后这个数组每个格子,不止存数据,还存储着该数据节点的父亲的所在下标(根节点没有父亲,存-1)。这种方法也可以表示整棵树,也即可以遍历到/找到任意的一个节点。何出此言?
struct TreeNode
{int data; //节点存储的数据int parent_i;//我这个节点的父亲的在数组的下标
};如果我们要找到任意一个节点,可以选择遍历这个数组,从而找到这个节点;然后如何找到这个从根到这个节点的路径呢?其实我们可以通过这个数组每个格子里面存储的父亲的下标,一直往父亲跳,一直跳到根即可,记录每个跳到的节点,其实这就是从根到该节点的路
径。

如上面这棵树,我们用数组存储父亲下标法,就是这样组织出这棵树的:
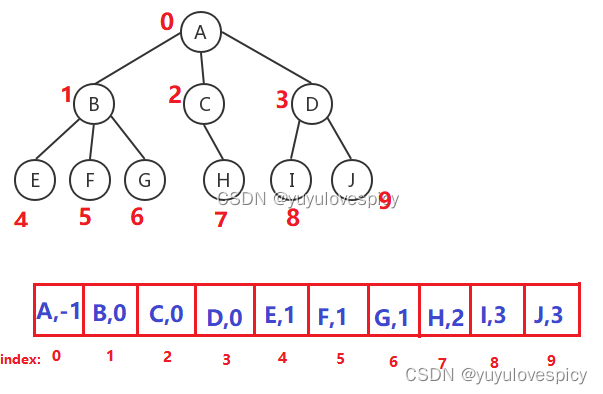
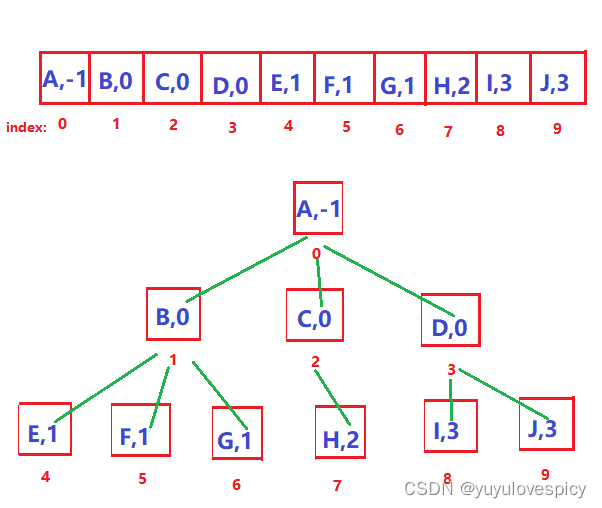
3.2.2 完全二叉树的数组表示法
完全二叉树由于其特殊性,在数组中存储表示可以也是非常方便的,而且也会有很多的性质使用,这个我们会放在后面一篇博客,关于数据结构堆的实现上具体讲解(想了解的话就关注我吧~),这种方法来表示完全二叉树也是非常优秀,非常的劲爆!!!
相关文章:

【数据结构必会基础】关于树,你所必须知道的亿些概念
目录 1.什么是树 1.1浅显的理解树 1.2 数据结构中树的概念 2.树的各种结构概念 2.1 节点的度 2.2 根节点/叶节点/分支节点 2.3 父节点/子节点 2.4祖先节点/子孙节点 2.5兄弟节点 2.6树的度 2.7节点的层次 2.8森林 3. 如何用代码表示一棵树 3.1链式结构 3.1.1 树节…...
)
设计模式的应用(已在大型项目中使用)
说明:开发语言:在本文中,使用的是C# 一、目录 •1 、单例模式 •2 、简单工厂模式 •3 、代理模式 •4 、观察者模式 •5 、外观模式 •6 、享元模式 •7 、命令模式 •8 、状态模式 •9 、发布订阅模式...

Git的相关用法
1.全局设置自己的git提交用户名和邮箱git config --global user.name 张三 git config --global user.email zsgmail.com即所有的提交都会用这个姓名和邮箱。如果不知道自己配置的是什么,可以查询下git config --global user.name git config --global user.email 或…...
Linux服务:Nginx反向代理与负载均衡
目录 一、Nginx反向代理 1、什么是代理 2、实现反向代理实验 ①实验拓扑 ②实验目的 ③实验过程 二、反向代理负载均衡 1、反向代理负载均衡调度算法 ①轮询算法 ②加权轮询算法 ③最小连接数算法 ④ip、url 哈希算法 ⑤响应时间fair算法 2、实现反向代理负载均…...

数据结构与算法——2.算法概述
这篇文章,我们来讲一下算法的概述,大致理解一下什么是算法。 目录 1.定义 2.生活实例 3.算法目标 4.实际案例 4.1案例一 4.2案例二 5.小结 1.定义 官方解释: 算法是指解题方案的准确而完整的描述,是一系列解决问题的清…...

BPMN2.0是什么,BPMN能解决企业流程管理中哪些问题?
一、前言: 在任何行业和企业中,一定存在着各式各样的流程,请假流程、报销流程、入职流程、离职流程、出差流程、合同审批流程、出入库流程等等…… 无论是管理者、技术人员还是业务人员,每天肯定也在使用各种流程,但…...

Java线程池的基本工作原理及案例
一、线程池的优点 线程池做的工作主要是控制运行的线程的数量,处理过程中将任务放入队列,然后在线程创建后启动这些任务,如果线程数量超过了最大数量超出数量的线程排队等候,等其它线程执行完毕,再从队列中取出任务来执行。 主要特点:线程复用;控制最大并发数;管理线程…...
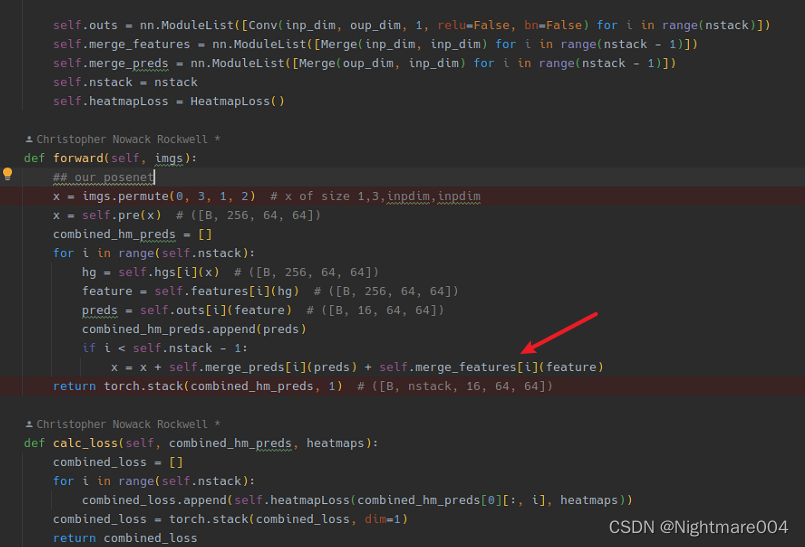
Stacked hourglass networks for human pose estimation代码学习
Stacked hourglass networks for human pose estimation https://github.com/princeton-vl/pytorch_stacked_hourglass 这是一个用于人体姿态估计的模型,只能检测单个人 作者通过重复的bottom-up(高分辨率->低分辨率)和top-down࿰…...
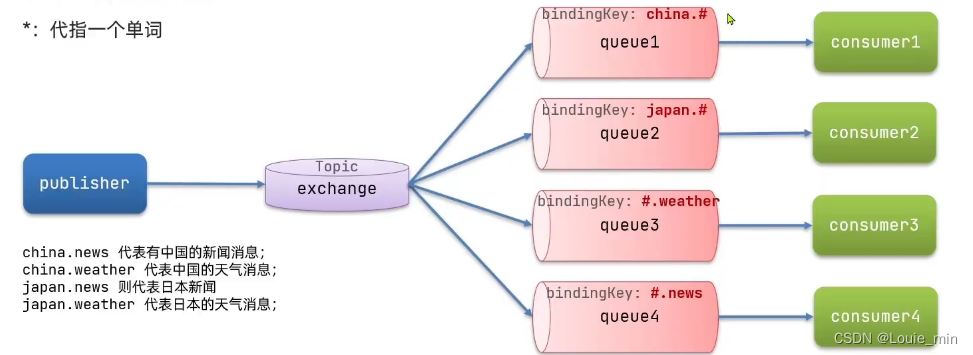
SpringCloud(五)MQ消息队列
MQ概念常见消息模型helloworld案例实现实现spring AMQP发送消息实现spring AMQP接收消息工作消息队列实现发布订阅模型Fanout Exchange实现DirectExchange实现TopicExchange实现DirectExchange 和FanoutExchange的差异DirectExchange 和TopicExchange的差异基于RabbitListener注…...

SQL语法基础汇总
三年前的存稿 默认端口号 3306 超级用户名 root 登录 mysql -uroot -p / mysql -uroot -proot 退出 exit / quit 服务器版本 SELECT VERSION(); 当前日期 SELECT NOW(); 当前用户 SELECT USER(); 备份 mysqldump -uroot -p 数据库名称 > 保存的路径 还原 create database1-…...

惠普星14Pro电脑开机不了显示错误代码界面怎么办?
惠普星14Pro电脑开机不了显示错误代码界面怎么办?有用户电脑开机之后,进入了一个错误界面,里面有一些错误代码。重启电脑之后依然是无法进入到桌面中,那么这个情况怎么去进行解决呢?我们可以重装一个新系统,…...
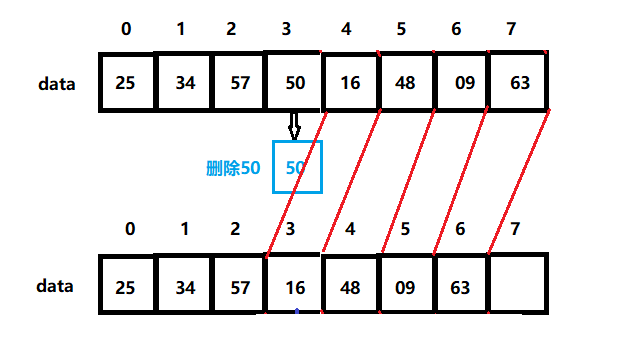
顺序表的构造及功能
定义顺序表是一种随机存储都结构,其特点是表中的元素的逻辑顺序与物理顺序相同。假设线性表L存储起始位置为L(A),sizeof(ElemType)是每个数据元素所占的存储空间的大小,则线性表L所对应的顺序存储如下图。顺序表的优缺点优点:随机…...
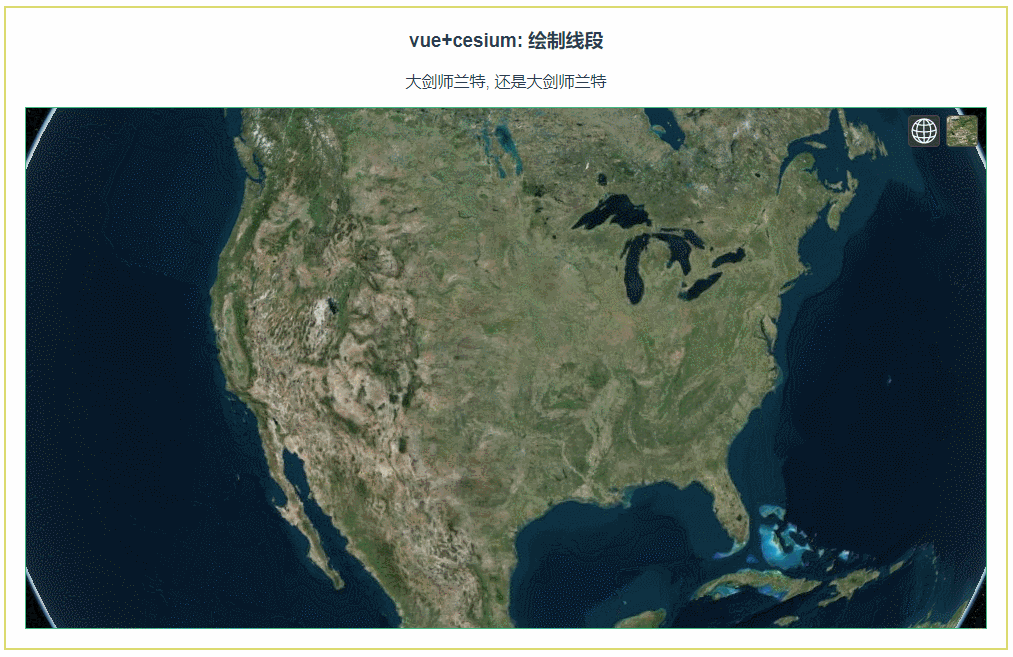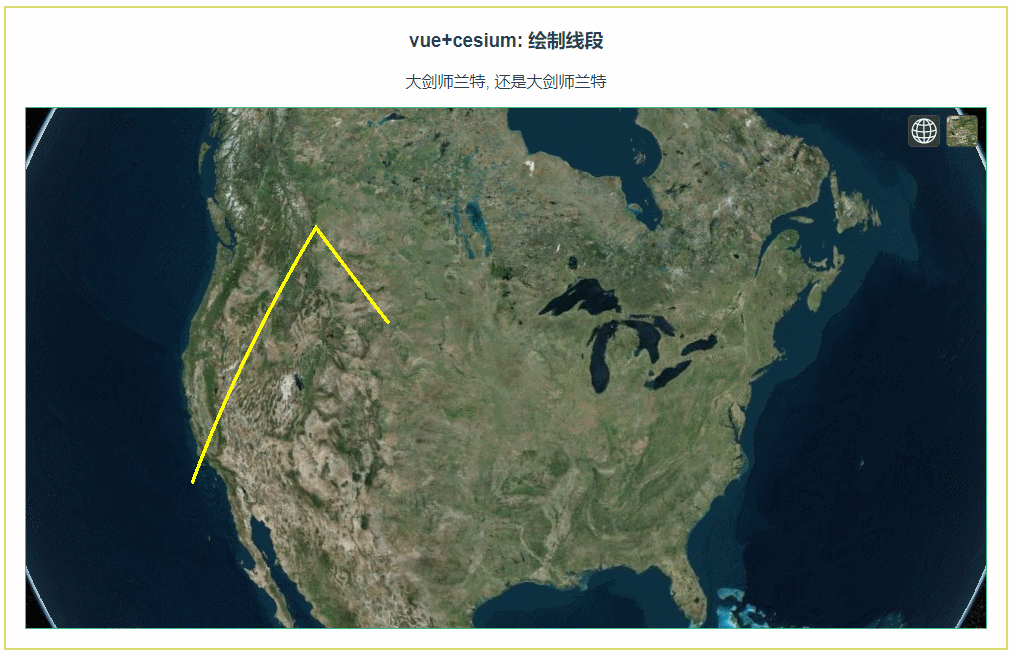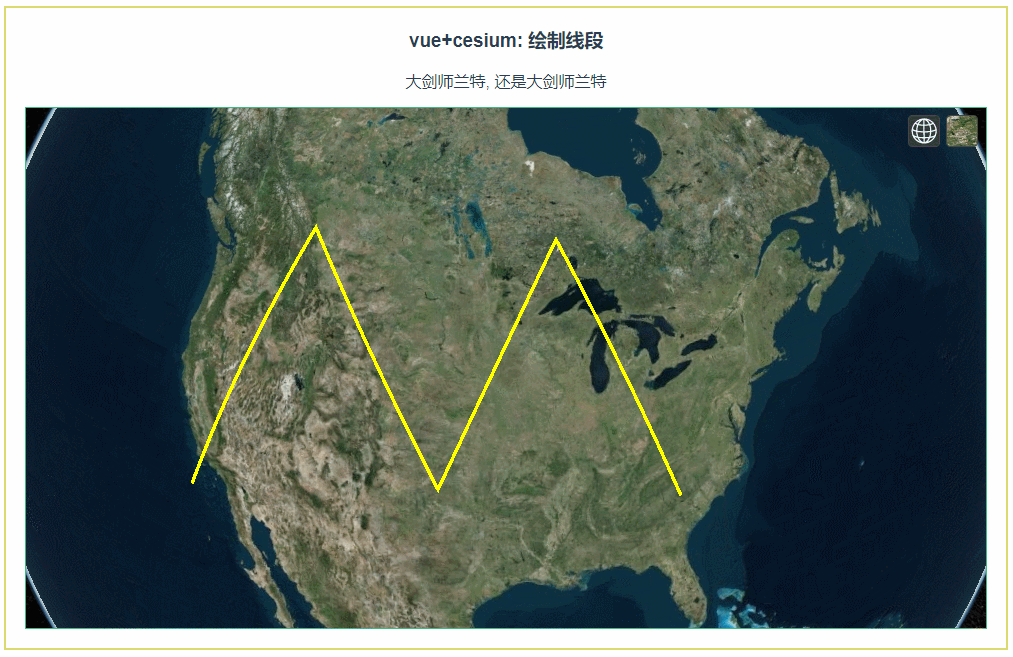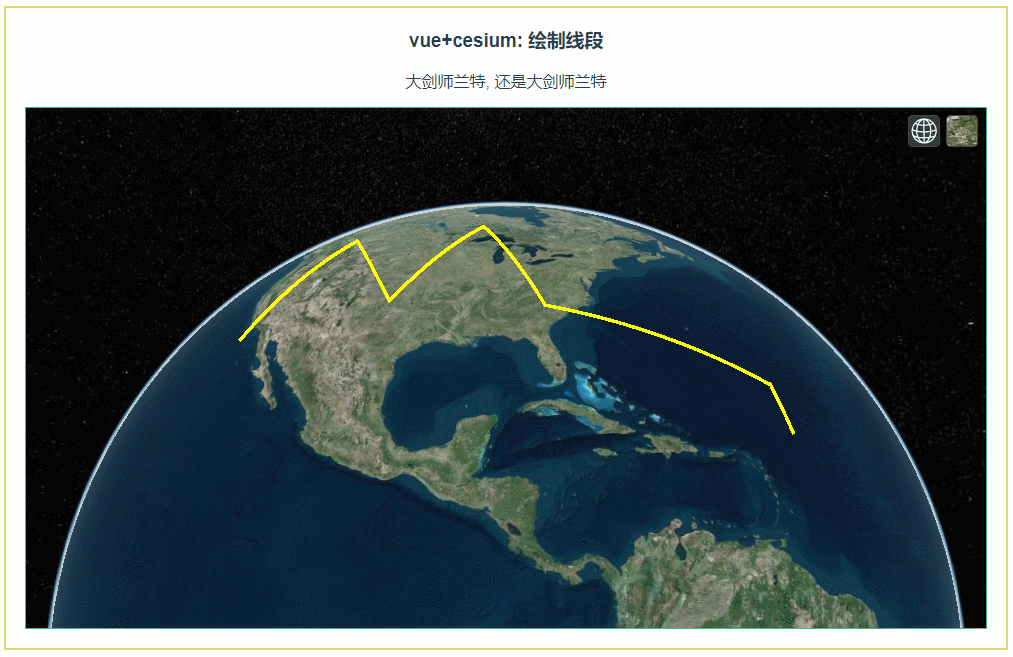
cesium: 绘制线段(008)
第008个 点击查看专栏目录 本示例的目的是介绍如何在vue+cesium中绘制线段,左键点击开始绘制,右键点击取消绘制 直接复制下面的 vue+cesium源代码,操作2分钟即可运行实现效果. 文章目录 示例效果配置方式示例源代码(共139行)相关API参考:专栏目标示例效果 配置方式 1)…...
HTML、CSS学习笔记4(3D转换、动画)
目录 一、空间转换(3D转换) 1.空间位移 语法: 取值:(正负均可) 透视: 2.空间旋转 3.立体呈现 二、动画(animation) 1.动画的使用 先定义动画 再调用定义好的动画 …...

java的分布式锁
什么是分布式锁 分布式锁是指分布式环境下,系统部署在多个机器中,实现多进程分布式互斥的一种锁。为了保证多个进程能看到锁,锁被存在公共存储(比如 Redis、Memcache、数据库等三方存储中),以实现多个进程并…...

17- TensorFlow实现手写数字识别 (tensorflow系列) (项目十七)
项目要点 模型创建: model Sequential()添加卷积层: model.add(Dense(32, activationrelu, input_dim100)) # 第一层需要 input_dim添加dropout: model.add(Dropout(0.2))添加第二次网络: model.add(Dense(512, activationrelu)) # 除了first, 其他层不要输入shape添加输出…...

Polkadot 基础
Polkadot Polkadot联合并保护了一个不断增长的专业区块链生态系统,称为parachains。Polkadot上的应用程序和服务可以安全地跨链通信,形成真正可互操作的去中心化网络的基础。 真正的互操作性 Polkadot支持跨区块链传输任何类型的数据或资产,…...
spring源码编译
spring源码编译1、安装gradle2、拉取源码3、配置gradle文件来源及镜像仓库4、预编译5、验证6、可能遇到的报错6.1、jdk.jfr不存在6.2、checkstyleMain6.3、org.gradle.api.artifacts.result.ComponentSelectionReason.getDescription()Ljava/lang/String6.4、其他jdk࿱…...

防盗链是什么?带你了解什么是防盗链
目录 什么是防盗链 防盗链的定义 防盗链的产生 防盗链的实现 什么是防盗链 防盗链其实就是采用服务器端编程,通过url过滤技术实现的防止盗链的软件。 比如:photo.abc.com/video.mp4 这个下载地址,如果没有装防盗链,别人就能轻…...

Linux基础命令-fdisk管理磁盘分区表
文章目录 fdisk 命令介绍 命令格式 基本参数 1)常用参数 2)fdisk菜单操作说明 创建一个磁盘分区 1)创建分区 2)创建交换分区 参考实例 1) 显示当前分区的信息 2) 显示每个磁盘的分区信息 命令…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
