pytorch-自动求导机制,构建计算图进行反向传播,需要注意inplace操作导致的报错,梯度属性变化
-
PyTorch 作为一个深度学习平台,在深度学习任务中比 NumPy 这个科学计算库强在哪里呢?一是 PyTorch 提供了自动求导机制,二是对 GPU 的支持。由此可见,自动求导 (autograd) 是 PyTorch,乃至其他大部分深度学习框架中的重要组成部分。
-
了解自动求导背后的原理和规则,对我们写出一个更干净整洁甚至更高效的 PyTorch 代码是十分重要的。但是,现在已经有了很多封装好的 API,我们在写一个自己的网络的时候,可能几乎都不用去注意求导这些问题,因为这些 API 已经在私底下处理好了这些事情。现在我们往往只需要,搭建个想要的模型,处理好数据的载入,调用现成的 optimizer 和 loss function,直接开始训练就好了。连需要设置
requires_grad=True的地方好像都没有。 -
torch.Tensor是这个包的核心类。如果设置.requires_grad为True,那么将会追踪所有对于该张量的操作。 当完成计算后通过调用.backward(),自动计算所有的梯度, 这个张量的所有梯度将会自动积累到.grad属性。要阻止张量跟踪历史记录,可以调用.detach()方法将其与计算历史记录分离,并禁止跟踪它将来的计算记录。 -
为了防止跟踪历史记录(和使用内存),可以将代码块包装在
with torch.no_grad():中。 在评估模型时特别有用,因为模型可能具有requires_grad = True的可训练参数,但是我们不需要梯度计算。 -
在自动梯度计算中还有另外一个重要的类
Function.Tensor和Function互相连接并生成一个非循环图,它表示和存储了完整的计算历史。 每个张量都有一个.grad_fn属性,这个属性引用了一个创建了Tensor的Function(除非这个张量是用户手动创建的,即,这个张量的grad_fn是None)。 -
Autograd是反向自动求导系统。概念 Autograd记录一个图表,记录创建的所有操作 执行操作时的数据,提供有向无环图 其叶子是输入张量,根是输出张量。 通过从根到叶跟踪此图,可以自动使用链式法则计算梯度。
-
计算图
-
首先,我们先简单地介绍一下什么是计算图(Computational Graphs),以方便后边的讲解。假设我们有一个复杂的神经网络模型,我们把它想象成一个错综复杂的管道结构,不同的管道之间通过节点连接起来,我们有一个注水口,一个出水口。我们在入口注入数据的之后,数据就沿着设定好的管道路线缓缓流动到出水口,这时候我们就完成了一次正向传播。
-
计算图通常包含两种元素,一个是 tensor,另一个是 Function。张量 tensor 不必多说,但是大家可能对 Function 比较陌生。这里 Function 指的是在计算图中某个节点(node)所进行的运算,比如加减乘除卷积等等之类的,Function 内部有
forward()和backward()两个方法,分别应用于正向、反向传播。 -
在我们做正向传播的过程中,除了执行
forward()操作之外,还会同时会为反向传播做一些准备,为反向计算图添加 Function 节点。在上边这个例子中,变量b在反向传播中所需要进行的操作是<ExpBackward>。
-
-
注意:grad在反向传播过程中是累加的(accumulated),这意味着每一次运行反向传播,梯度都会累加之前的梯度,所以一般在反向传播之前需把梯度清零。
-
通过 “xiaopl” 的例子学习
-
import torch from torchvision.models import mobilenet_v3_small,vgg11 from torchviz import make_dot # 以VGGNet11为例,前向传播 x = torch.rand(8, 3, 224, 224) model = vgg11() y = model(x) # 构造图对象,3种方式 g = make_dot(y) # g = make_dot(y, params=dict(model.named_parameters())) # g = make_dot(y, params=dict(list(model.named_parameters()) + [('x', x)])) # 保存图像 # g.view() # 生成 Digraph.gv.pdf,并自动打开 g.render(filename='vgg11', view=False) # 保存为 graph.pdf,参数view表示是否打开pdf -

-
l1 = input x w1 l2 = l1 + w2 l3 = l1 x w3 l4 = l2 x l3 loss = mean(l4) -
这个例子比较简单,涉及的最复杂的操作是求平均,但是如果我们把其中的加法和乘法操作换成卷积,那么其实和神经网络类似。我们可以简单地画一下它的计算图:
-

-
下面给出了对应的代码,我们定义了
input,w1,w2,w3这三个变量,其中input不需要求导结果。根据 PyTorch 默认的求导规则,对于l1来说,因为有一个输入需要求导(也就是w1需要),所以它自己默认也需要求导,即requires_grad=True。在整张计算图中,只有input一个变量是requires_grad=False的。正向传播过程的具体代码如下:-
import torch input = torch.ones([2, 2], requires_grad=False) w1 = torch.tensor(2.0, requires_grad=True) w2 = torch.tensor(3.0, requires_grad=True) w3 = torch.tensor(4.0, requires_grad=True) l1 = input * w1 l2 = l1 + w2 l3 = l1 * w3 l4 = l2 * l3 loss = l4.mean() #l1.retain_grad() # 非叶节点张量查看需要设置 #loss.retain_grad() print(w1.data, w1.grad, w1.grad_fn) print(l1.data, l1.grad, l1.grad_fn) print(loss.data, loss.grad, loss.grad_fn)
-
-
tensor(2.) None None
tensor([[2., 2.],
[2., 2.]]) None <MulBackward0 object at 0x000001B9808798B0>
tensor(40.) None <MeanBackward0 object at 0x000001B9802699D0>
-
可以看到,变量
l1的grad_fn储存着乘法操作符<MulBackward0>,用于在反向传播中指导导数的计算。而w1是用户自己定义的,不是通过计算得来的,所以其grad_fn为空;同时因为还没有进行反向传播,grad的值也为空。接下来,我们看一下如果要继续进行反向传播,计算图应该是什么样子:-

-
反向图也比较简单,从
loss这个变量开始,通过链式法则,依次计算出各部分的导数。【深一点学习】BP网络,结合数学推导的代码实现_羞儿的博客-CSDN博客 -
loss.backward() print(w1.grad, w2.grad, w3.grad) print(l1.grad, l2.grad, l3.grad, l4.grad, loss.grad)
-
tensor(28.) tensor(8.) tensor(10.)
None None None None None
-
首先我们需要注意一下的是,在之前写程序的时候我们给定的
w们都是一个常数,利用了广播的机制实现和常数和矩阵的加法乘法,比如w2 + l1,实际上我们的程序会自动把w2扩展成 [[3.0, 3.0], [3.0, 3.0]],和l1的形状一样之后,再进行加法计算,计算的导数结果实际上为 [[2.0, 2.0], [2.0, 2.0]],为了对应常数输入,所以最后w2的梯度返回为矩阵之和 8 。另外还有一个问题,虽然w开头的那些和我们的计算结果相符,但是为什么l1,l2,l3,甚至其他的部分的求导结果都为空呢?想要解答这个问题,我们得明白什么是叶子张量。 -
叶子张量
-
对于任意一个张量来说,我们可以用 tensor.is_leaf 来判断它是否是叶子张量(leaf tensor)。在反向传播过程中,只有 is_leaf=True 的时候,需要求导的张量的导数结果才会被最后保留下来。
-
对于 requires_grad=False 的 tensor 来说,我们约定俗成地把它们归为叶子张量。但其实无论如何划分都没有影响,因为张量的 is_leaf 属性只有在需要求导的时候才有意义。
-
我们真正需要注意的是当
requires_grad=True的时候,如何判断是否是叶子张量:当这个 tensor 是用户创建的时候,它是一个叶子节点,当这个 tensor 是由其他运算操作产生的时候,它就不是一个叶子节点。 -
print(input.is_leaf,w1.is_leaf,w2.is_leaf,w3.is_leaf,l1.is_leaf,l2.is_leaf,l3.is_leaf,l4.is_leaf,loss.is_leaf)
-
True True True True False False False False False
-
为什么要搞出这么个叶子张量的概念出来?原因是为了节省内存(或显存)。我们来想一下,那些非叶子结点,是通过用户所定义的叶子节点的一系列运算生成的,也就是这些非叶子节点都是中间变量,一般情况下,用户不会去使用这些中间变量的导数,所以为了节省内存,它们在用完之后就被释放了。
-
我们回头看一下之前的反向传播计算图,在图中的叶子节点用绿色标出了。可以看出来,被叫做叶子,可能是因为游离在主干之外,没有子节点,因为它们都是被用户创建的,不是通过其他节点生成。对于叶子节点来说,它们的
grad_fn属性都为空;而对于非叶子结点来说,因为它们是通过一些操作生成的,所以它们的grad_fn不为空。 -
通过使用
tensor.retain_grad()就可以保留中间变量的导数:-
print(input.requires_grad,input.is_leaf,input.grad) print(l1.requires_grad,l1.is_leaf,l1.grad) print(loss.requires_grad,loss.is_leaf,loss.grad) l1.retain_grad() loss.retain_grad() loss.backward() # 重新运行,主要不要二次反向传播 print(input.requires_grad,input.is_leaf,input.grad) print(l1.requires_grad,l1.is_leaf,l1.grad) print(loss.requires_grad,loss.is_leaf,loss.grad)
-
False True None
True False None
True False None
False True None
True False tensor([[7., 7.],
[7., 7.]])
True False tensor(1.)
-
input 其实很像神经网络输入的图像,w1, w2, w3 则类似卷积核的参数,而 l1, l2, l3, l4 可以表示4个卷积层输出,如果我们把节点上的加法乘法换成卷积操作的话。实际上这个简单的模型,很像我们平时的神经网络的简化版。
-
inplace 操作
-
inplace 指的是在不更改变量的内存地址的情况下,直接修改变量的值。
-
每次 tensor 在进行 inplace 操作时,变量
_version就会加1,其初始值为0。在正向传播过程中,求导系统记录的b的 version 是0,但是在进行反向传播的过程中,求导系统发现b的 version 变成1了,所以就会报错了。但是还有一种特殊情况不会报错,就是反向传播求导的时候如果没用到b的值(比如y=x+1, y 关于 x 的导数是1,和 x 无关),自然就不会去对比b前后的 version 了,所以不会报错。 -
a = torch.tensor([1.0, 3.0], requires_grad=True) b = a + 2 print(b._version) # 0 loss = (b * b).mean() b[0] = 1000.0 print(b._version) # 1 loss.backward() -
0 1 RuntimeError: one of the variables needed for gradient computation has been modified by an inplace operation: [torch.FloatTensor [2]], which is output 0 of struct torch::autograd::CopySlices, is at version 1; expected version 0 instead. Hint: enable anomaly detection to find the operation that failed to compute its gradient, with torch.autograd.set_detect_anomaly(True).
-
-
上边我们所说的情况是针对非叶子节点的,对于
requires_grad=True的叶子节点来说,要求更加严格了,甚至在叶子节点被使用之前修改它的值都不行。这个意思通俗一点说就是你的一顿 inplace 操作把一个叶子节点变成了非叶子节点了。我们知道,非叶子节点的导数在默认情况下是不会被保存的,这样就会出问题了。举个小例子:-
a = torch.tensor([10., 5., 2., 3.], requires_grad=True) print(a, a.is_leaf) # tensor([10., 5., 2., 3.], requires_grad=True) True a[:] = 0 print(a, a.is_leaf) # RuntimeError: a view of a leaf Variable that requires grad is being used in an in-place operation. loss = (a*a).mean() loss.backward() -
在进行对
a的重新 inplace 赋值之后,表示了 a 是通过 copy operation 生成的,grad_fn都有了,所以自然而然不是叶子节点了。本来是该有导数值保留的变量,现在成了导数会被自动释放的中间变量了,所以 PyTorch 就给你报错了。 -
不等到你调用 backward,只要你对需要求导的叶子张量使用了这些操作,马上就会报错。那是不是需要求导的叶子节点一旦被初始化赋值之后,就不能修改它们的值了呢?我们如果在某种情况下需要重新对叶子变量赋值该怎么办呢?有办法!
-
# 方法一 a = torch.tensor([10., 5., 2., 3.], requires_grad=True) print(a, a.is_leaf, id(a)) a.data.fill_(10.) # 或者 a.detach().fill_(10.) print(a, a.is_leaf, id(a)) loss = (a*a).mean() loss.backward() print(a.grad) # 方法二 a = torch.tensor([10., 5., 2., 3.], requires_grad=True) print(a, a.is_leaf) with torch.no_grad():a[:] = 10. print(a, a.is_leaf) loss = (a*a).mean() loss.backward() print(a.grad)
-
tensor([10., 5., 2., 3.], requires_grad=True) True 2126921359984
tensor([10., 10., 10., 10.], requires_grad=True) True 2126921359984
tensor([5., 5., 5., 5.])
tensor([10., 5., 2., 3.], requires_grad=True) True
tensor([10., 10., 10., 10.], requires_grad=True) True
tensor([5., 5., 5., 5.])
-
修改的方法有很多种,核心就是修改那个和变量共享内存,但
requires_grad=False的版本的值,比如通过tensor.data或者tensor.detach()。需要注意的是,要在变量被使用之前修改,不然等计算完之后再修改,还会造成求导上的问题,会报错的。 -
为什么 PyTorch 的求导不支持绝大部分 inplace 操作呢?从上边我们也看出来了,因为真的很 tricky。比如有的时候在一个变量已经参与了正向传播的计算,之后它的值被修改了,在做反向传播的时候如果还需要这个变量的值的话,我们肯定不能用那个后来修改的值吧,但没修改之前的原始值已经被释放掉了,我们怎么办?
- 一种可行的办法就是在 Function 做 forward 的时候每次都开辟一片空间储存当时输入变量的值,这样无论之后它们怎么修改,都不会影响了,反正我们有备份在存着。但这样有什么问题?这样会导致内存(或显存)使用量大大增加。因为我们不确定哪个变量可能之后会做 inplace 操作,所以我们每个变量在做完 forward 之后都要储存一个备份,成本太高了。除此之外,inplace operation 还可能造成很多其他求导上的问题。
-
总之,在实际写代码的过程中,没有必须要用 inplace operation 的情况,而且支持它会带来很大的性能上的牺牲,所以 PyTorch 不推荐使用 inplace 操作,当求导过程中发现有 inplace 操作影响求导正确性的时候,会采用报错的方式提醒。但这句话反过来说就是,因为只要有 inplace 操作不当就会报错,所以如果我们在程序中使用了 inplace 操作却没报错,那么说明我们最后求导的结果是正确的,没问题的。
-
动态图,静态图
- 所谓动态图,就是每次当我们搭建完一个计算图,然后在反向传播结束之后,整个计算图就在内存中被释放了。静态图,每次都先设计好计算图,需要的时候实例化这个图,然后送入各种输入,重复使用,只有当会话结束的时候创建的图才会被释放。
-
静态图,每次都先设计好计算图,需要的时候实例化这个图,然后送入各种输入,重复使用,只有当会话结束的时候创建的图才会被释放。
-
正是因为 PyTorch 的两大特性:动态图和 eager execution,所以它用起来才这么顺手,简直就和写 Python 程序一样舒服,debug 也非常方便。除此之外,我们从之前的描述也可以看出,PyTorch 十分注重占用内存(或显存)大小,没有用的空间释放很及时,可以很有效地利用有限的内存。
-
Automatic differentiation package - torch.autograd — PyTorch 1.13 documentation
一样舒服,debug 也非常方便。除此之外,我们从之前的描述也可以看出,PyTorch 十分注重占用内存(或显存)大小,没有用的空间释放很及时,可以很有效地利用有限的内存。 -
Automatic differentiation package - torch.autograd — PyTorch 1.13 documentation
相关文章:

pytorch-自动求导机制,构建计算图进行反向传播,需要注意inplace操作导致的报错,梯度属性变化
PyTorch 作为一个深度学习平台,在深度学习任务中比 NumPy 这个科学计算库强在哪里呢?一是 PyTorch 提供了自动求导机制,二是对 GPU 的支持。由此可见,自动求导 (autograd) 是 PyTorch,乃至其他大部分深度学习框架中的重…...
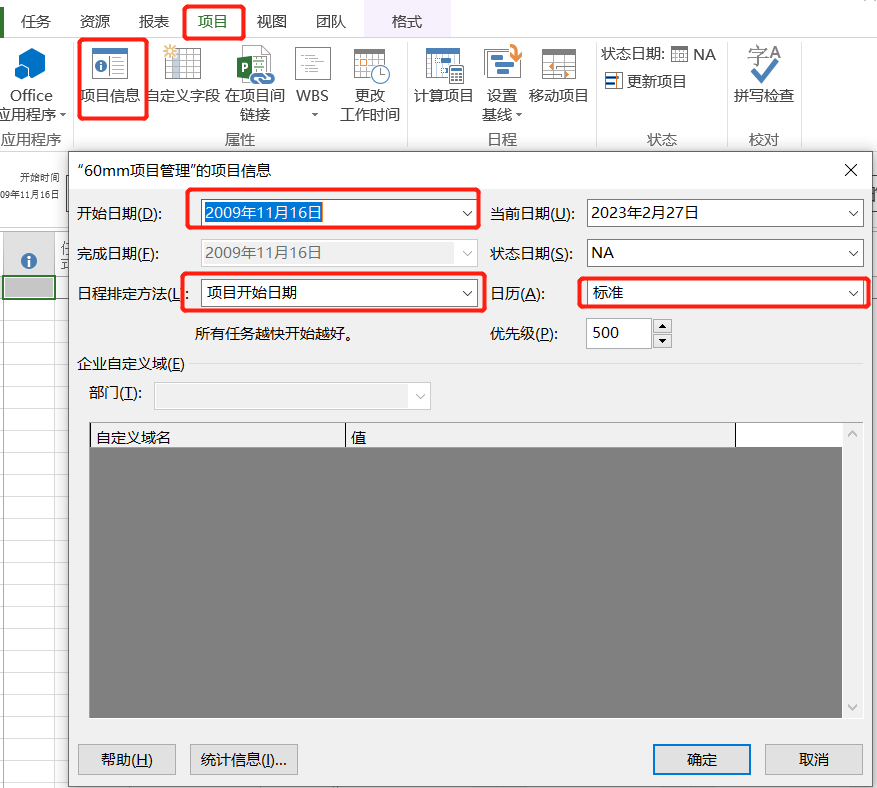
【Project】项目管理软件学习笔记
一、前言使用Project制定项目计划步骤大致如下:以Project2013为例,按照上图步骤指定项目计划。二、实施2.1 创建空白项目点击文件——新建——空白项目,即完成了空白项目的创建,在此我把该项目保存为60mm项目管理.mpp,…...

【算法设计-分治思想】快速幂与龟速乘
文章目录1. 快速幂2. 龟速乘3. 快速幂取模4. 龟速乘取模5. 快速幂取模优化1. 快速幂 算法原理: 计算 311: 311 (35)2 x 335 (32)2 x 332 3 x 3仅需计算 3 次,而非 11 次 计算 310: 310 (35)235 (32)2 x 332 3 x 3仅需计算…...
 如何保证数据的不重复和不丢失)
Kafka(十一) 如何保证数据的不重复和不丢失
数据不丢失 1)从生产端:acks -1,(ack应答机制)从生产端到节点端,当所有isr集合里的节点备份完毕后返回成功; 2)从节点端:每个partition至少需要一个isr节点࿰…...
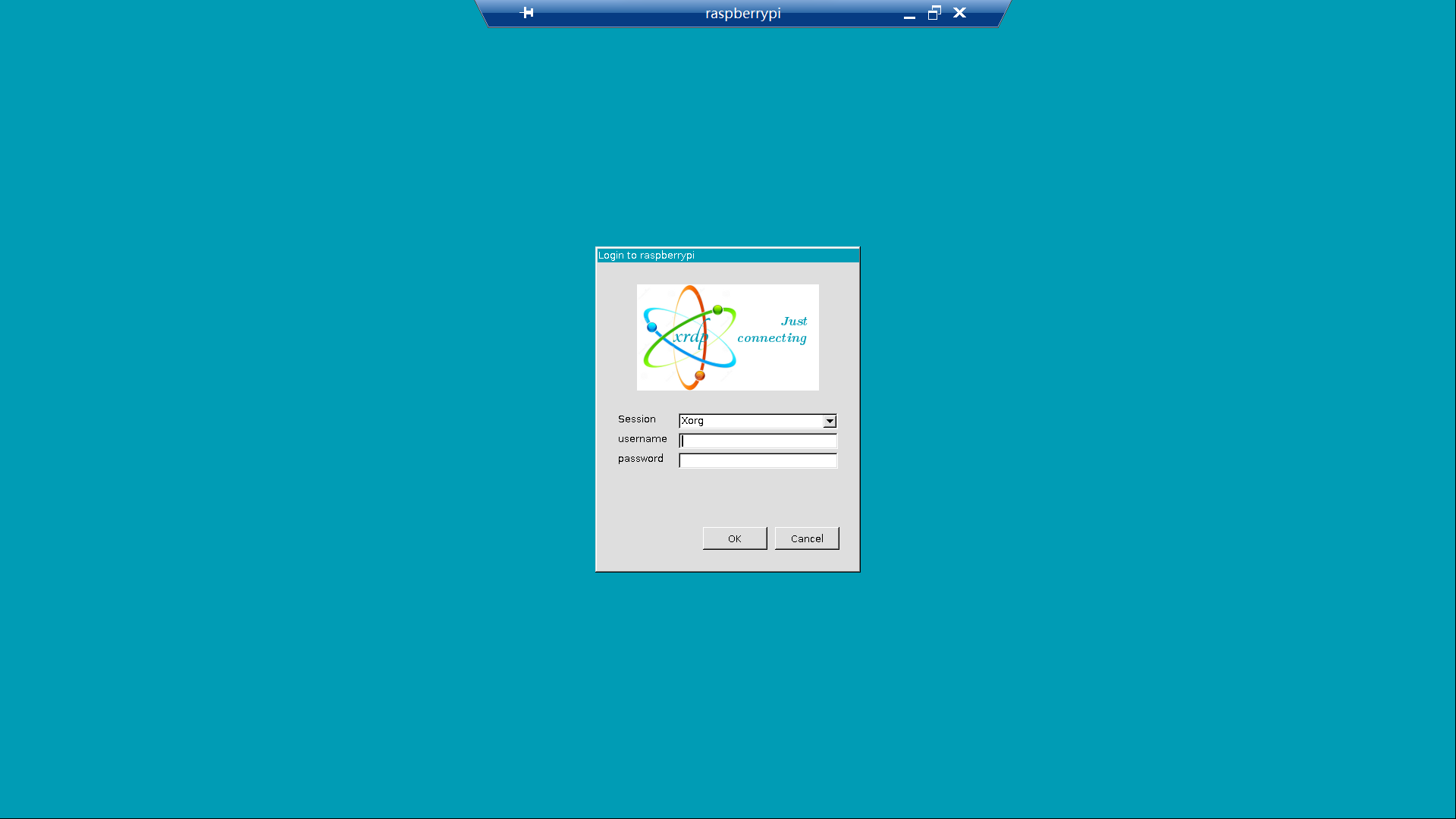
解决树莓派 bullseye (11) 系统无法通过 xrdp 远程连接的问题
我手上有一台树莓派 4B,使用官方镜像烧录器烧录老版本操作系统 buster (10) 时可以正常通过 Windows 远程桌面连接上,但换成最新的 bullseye (11) 系统后却无法正常连接远程桌面。 问题复现: 使用官方镜像烧录器烧录,配置用户名为…...
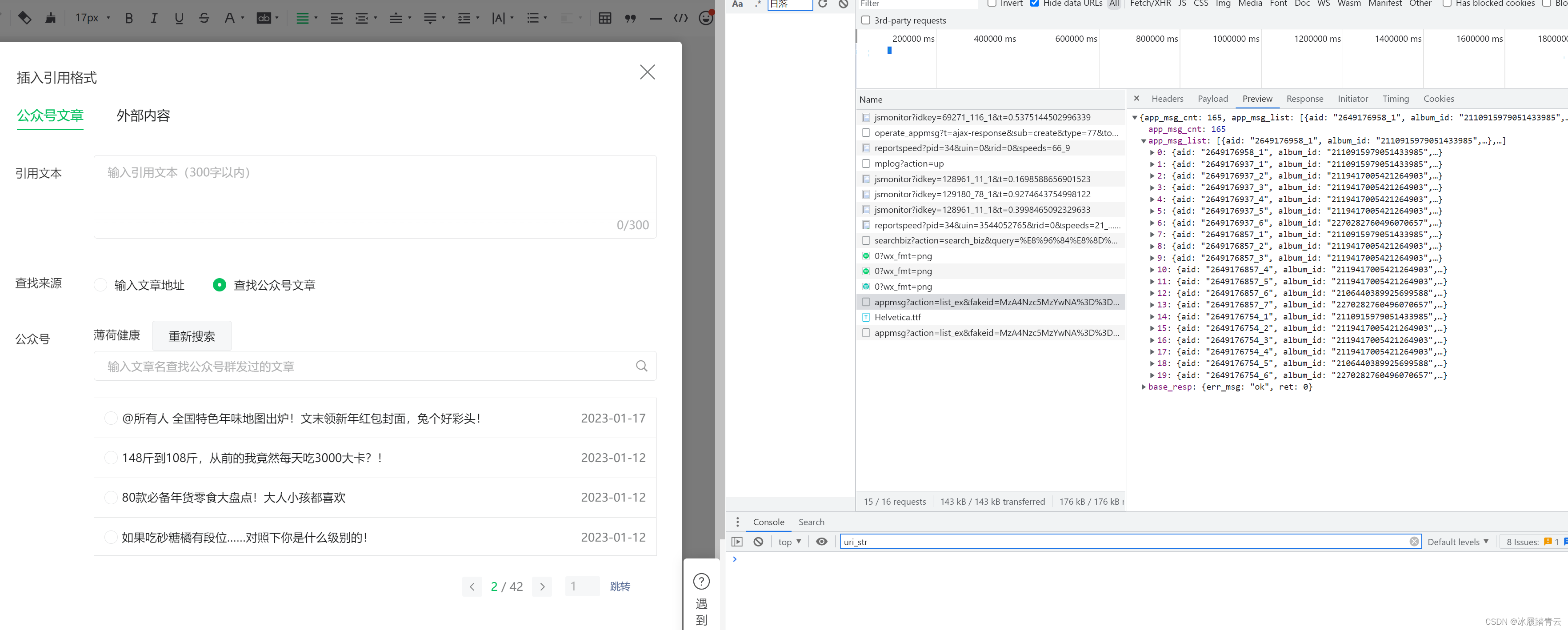
微信公众号历史作品定向采集
最近有遇到微信公众号历史作品采集的需求,这里做一下记录, 登录自己注册好的的微信公众号后台进入创作界面,点击右上角的引用: 弹出如下界面: 选择查找公众号文章,输入要查找的公众号: 回车: 同时就可以打开F12开始抓包,选择公众号点击进入: appmsg?action=li…...
)
Vue学习笔记(3)
3.1 计算属性和监视属性 3.1.1 计算属性 计算属性是一种计算值的方式,可以根据其他属性的值来动态地计算新的属性值。计算属性可以缓存计算结果,当依赖的属性发生改变时,才会重新计算。在Vue中,可以使用computed选项来定义计算属…...

Marshmallow 库
文章目录Marshmallow 库介绍使用序列化反序列化参数介绍schema参数fields 参数钩子函数内置验证器Meta 属性Marshmallow 库 介绍 marshmallow是一个用来将复杂的orm对象与python原生数据类型之间相互转换的库,简而言之,就是实现object -> dict&#…...

【BN层的作用】论文阅读 | How Does Batch Normalization Help Optimization?
前言:15年Google提出Batch Normalization,成为深度学习最成功的设计之一,18年MIT团队将原论文中提出的BN层的作用进行了一一反驳,重新揭示BN层的意义 2015年Google团队论文:【here】 2018年MIT团队论文:【h…...
用法的详细介绍)
re.sub()用法的详细介绍
一、前言 在字符串数据处理的过程中,正则表达式是我们经常使用到的,python中使用的则是re模块。下面会通过实际案例介绍 re.sub() 的详细用法,该函数主要用于替换字符串中的匹配项。 二、函数原型 首先从源代码来看一下该函数原型…...

【Python数据挖掘入门】2.2文本分析-中文分词(jieba库cut方法/自定义词典load_userdict/语料库分词)
中文分词就是将一个汉字序列切分成一个一个单独的词。例如: 另外还有停用词的概念,停用词是指在数据处理时,需要过滤掉的某些字或词。 一、jieba库 安装过程见:https://blog.csdn.net/momomuabc/article/details/128198306 ji…...
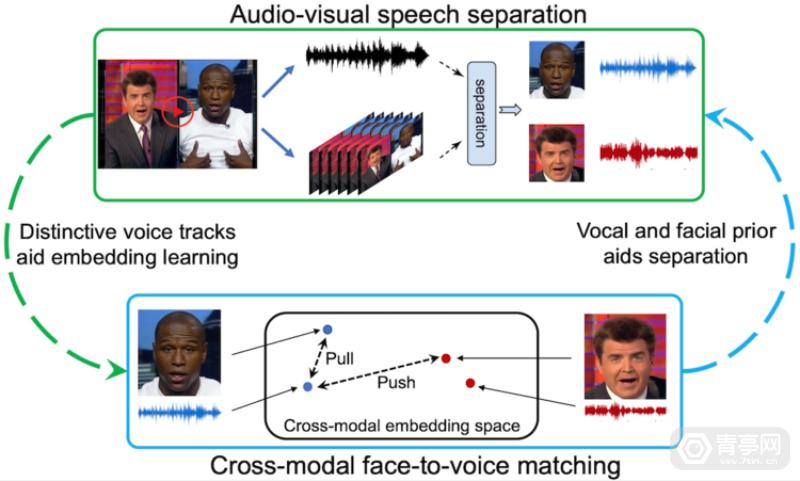
Meta利用视觉信息来优化3D音频模型,未来将用于AR/VR
我们知道,Meta为了给AR眼镜打造智能助手,专门开发了第一人称视觉模型和数据集。与此同时,该公司也在探索一种将视觉和语音融合的AI感知方案。相比于单纯的语音助手,同时结合视觉和声音数据来感知环境,可进一步增强智能…...
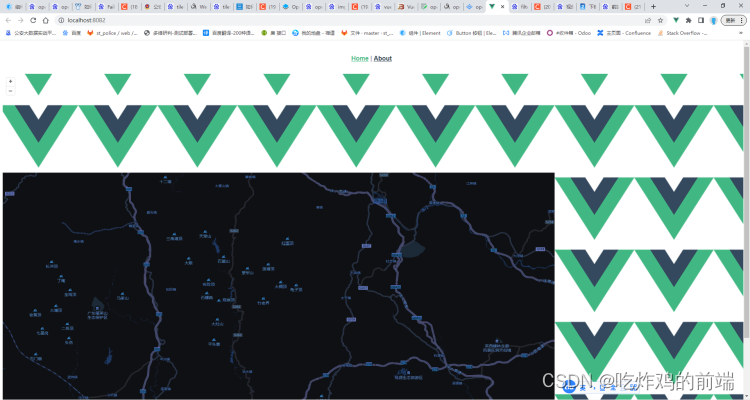
openlayers加载离线地图并实现深色地图
问题背景 我们自己一直使用的openlayergeoserver自己发布的地图,使用的是矢量地图。但是由于政府地图大都使用为天地图,所以需要将geoserver的矢量地图更改为天地图,并且依旧是搭配openlayers来使用。 解决步骤 一:加载离线地图&a…...

socket,tcp,http三者之间的区别和原理
目录 一、OSI模型也称七层网络模型 1、TCP/IP连接 1.1三次握手与四次挥手的简单理解:(面试重点) 1.2面试考题:如果已经建立了连接,但是客户端突然出现故障了怎么办? 1.3 socket、tcp、http三者之间有什…...

红日(vulnstack)1 内网渗透ATTCK实战
环境准备 靶机链接:百度网盘 请输入提取码 提取码:sx22 攻击机系统:kali linux 2022.03 网络配置: win7配置: kali配置: kali 192.168.1.108 192.168.111.129 桥接一块,自定义网卡4 win7 1…...

ik 分词器怎么调用缓存的词库
IK 分词器是一个基于 Java 实现的中文分词器,它支持在分词时调用缓存的词库。 要使用 IK 分词器调用缓存的词库,你需要完成以下步骤: 创建 IK 分词器实例 首先,你需要创建一个 IK 分词器的实例。可以通过以下代码创建一个 IK 分…...
ROS1/2机器人操作系统与时间Time的不解之缘
时间对于机器人操作系统非常重要。所有机器人类的编程中所涉及的变量如果需要在网络中传输都需要这个数据结构的时间戳。宏观上,ROS1、ROS2各版本都有官方支持的时间节点。ROS时钟--支持时间倒计时小工具效果如下:如果要部署机器人操作系统,R…...
)
华为OD机试真题2022(JAVA)
华为机试题库已换 →→→ 华为OD机试2023(JAVA) 以下题目为旧版题库,供大家课外消遣 基础题: 序号题目分值1查找众数及中位数1002出错的或电路1003连续字母长度1004分班1005计算面积1006最远足迹1007判断一组不等式是否满足约束…...
【3】MyBatis+Spring+SpringMVC+SSM整合一套通关
三、SpringMVC 1、SpringMVC简介 1.1、什么是MVC MVC是一种软件架构的思想,将软件按照模型、视图、控制器来划分 M:Model,模型层,指工程中的JavaBean,作用是处理数据 JavaBean分为两类: 一类称为实体…...
)
20道前端高频面试题(附答案)
ES6新特性 1.ES6引入来严格模式变量必须声明后在使用函数的参数不能有同名属性, 否则报错不能使用with语句 (说实话我基本没用过)不能对只读属性赋值, 否则报错不能使用前缀0表示八进制数,否则报错 (说实话我基本没用过)不能删除不可删除的数据, 否则报错不能删除变量delete p…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
