放苹果HJ61
入门题目
把m个同样的苹果放在n个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?
注意:如果有7个苹果和3个盘子,(5,1,1)和(1,5,1)被视为是同一种分法。
示例1
输入:
7 3
输出:
8
1 明确子问题是什么?
m个苹果,n个盘子,他们之间存在的关系要么 m 大于 n , m等于 n,或者 m 小于n ;
所有盘子都放苹果的对立事件是什么?
所有盘子都放苹果的对立事件是至少有一个盘子没有放置苹果。因为在所有的盘子都放置了苹果的情况下,没有盘子是没有放置苹果的,所以所有盘子都放苹果和至少有一个盘子没有放置苹果是互为对立事件。换句话说,如果一个事件发生了,那么另一个事件一定不会发生。
我们定义 dp[ m] [n] 为,m个苹果 ,n个盘子时,一共的分法。就是有两种放苹果的情况,要么n个盘子都放满,要么至少空一个盘子。
dp[ m] [n] = n个盘子都放满的放法 + 至少空一个盘子的方法
n个盘子都放满的方法 : 即要保证所有的盘子中至少都有一个,其他的随便放,所以每个盘子都减去一个苹果,共减去n个苹果即m-n 个,即变成了 m-n 个苹果放在n 个盘子中的放法 ,dp[m-n] [n] 。
至少空一个盘子的方法 :dp[m] [n-1]
保证子问题之间互斥,不重叠。
2 初始值
1 | 1 | 1 |
1 | 0 | 0 |
1 | 0 | 0 |
1 | 0 | 0 |
1 | 0 | 0 |
1 | 0 | 0 |
1 | 0 | 0 |
1 | 0 | 0 |
3 子问题的递推关系
if m< n : # 苹果数量少于盘子数量 100 个苹果放在 5 个盘子的放法数量和 5个苹果放在5个盘子的放法数量一样dp[m][n] = dp[m][m]else m>n :# 所有的盘子都不空的情况 + 存在一个盘子空的情况dp[m][n] = dp[m-n][n] + dp[m][n-1] 4 确定DP数组的计算顺序
递推
defdfs(m,n) :ifm==0 :return1 ; ifn==1 :return1 ; # 只有一个盘子就只有一个放法 ifm<n : returndfs(m,m)# 没有空盘子的放法(每个盘子都至少一个苹果) + 至少一个盘子空着的方法returndfs(m-n, n) +dfs(m, n-1)if__name__=='__main__' :m,n=map(int,(input().split()) )res=dfs(m,n)print(res) 动态规划
# import numpy as np defdfs(m,n) :ifm==0 :return1 ; ifn==1 :return1 ; # 只有一个盘子就只有一个放法 ifm<n : returndfs(m,m)# 没有空盘子的放法 + 至少一个盘子空着的方法returndfs(m-n, n) +dfs(m, n-1)if__name__=='__main__' :m,n=map(int,(input().split()) )# res = dfs(m,n)# print(res)# dp = np.zeros([m+1,n+1],dtype=int)dp= [[0foriinrange(n+1)] foriinrange(m+1)]# 初始化foriinrange(1,n+1): dp[0][i] =1 ; forjinrange(1,m+1): dp[j][1] =1 ; foriinrange(1,m+1) :forjinrange(1,n+1) : # 如果苹果数量少于盘子ifi<j : dp[i][j] =dp[i][j-1]else :# dp[i][j] 即每个状态# dp[i][j] =dp[i-j][j] +dp[i][j-1]print(dp[m][n]) 相关文章:

放苹果HJ61
入门题目 把m个同样的苹果放在n个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?注意:如果有7个苹果和3个盘子,(5,1,1)和(1,5&#…...

Windows下,OPC UA移植,open62541移植
OPC通信标准的核心是互通性 (Interoperability) 和标准化 (Standardization) 问题。传统的OPC技术在控制级别很好地解决了硬件设备间的互通性问题,在企业层面的通信标准化是同样需要的。OPC UA之前的访问规范都是基于微软的COM/DCOM技术, 这会给新增层面的通信带来不可根除的…...
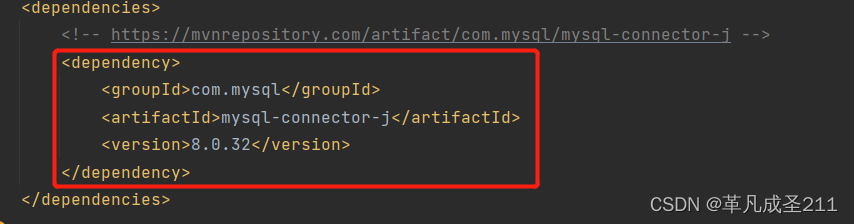
【Tomcat与Servlet篇1】认识Tomcat与Maven
目录 一、什么是Tomcat 二、Tomcat的几个重要目录 conf文件编辑 Server.xml logs文件 Webapps目录 三、如何使用Tomcat 但是,如果出现了点击之后进行闪退的情况,那又是怎么回事呢? 原因1:环境变量没有配置 原因2&#…...

C++类和对象:拷贝构造函数和运算符重载
目录 一. 拷贝构造函数 1.1 什么是拷贝构造函数 1.2 编译器默认生成的拷贝构造函数 1.3 拷贝构造函数特性总结 二. 运算符重载 2.1 运算符重载概述 2.2 比较运算符重载(> > < <) 2.2.1 >运算符的重载 2.2.2 运算符的重载 2.…...
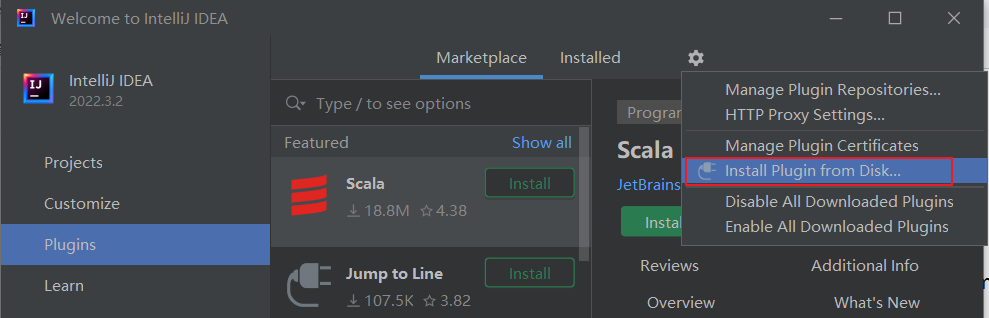
【IntelliJ IDEA】idea plugins搜索不出来,如何找到插件的解决方案
一、背景描述安装好IDEA后,想下载一些插件来使用,因为IDEA非常方便的一点就是插件使用非常的方便,但是经常会发现进入到插件市场无法搜索到插件的情况,这个时候就有点烦人了。那么怎么解决这个问题呢?以下会把我能想到…...

移动端自动化测试(一)appium环境搭建
自动化测试有主要有两个分类,接口自动化和ui自动化,ui自动化呢又分移动端的和web端的,当然还有c/s架构的,这种桌面程序应用的自动化,使用QTP,只不过现在没人做了。 web自动化呢,现在基本上都是…...
5 逻辑回归及Python实现
1 主要思想 分类就是分割数据: 两个条件属性:直线;三个条件属性:平面;更多条件属性:超平面。 使用数据: 5.1,3.5,0 4.9,3,0 4.7,3.2,0 4.6,3.1,0 5,3.6,0 5.4,3.9,0 . . . 6.2,2.9,1 5.1,2.5…...
技术干货 | Modelica建模秘籍之状态变量
在很多领域都有“系统”这个概念,它描述的往往是一些复杂关系的总和。假如我们将系统看做一个黑箱,那么,在系统的作用下,外界的输入有时会产生令人意想不到的输出,“蝴蝶效应”就是其中的典型案例。图1 一只南美洲亚马…...

LeetCode 2574. 左右元素和的差值
给你一个下标从 0 开始的整数数组 nums ,请你找出一个下标从 0 开始的整数数组 answer ,其中: answer.length nums.length answer[i] |leftSum[i] - rightSum[i]| 其中: leftSum[i] 是数组 nums 中下标 i 左侧元素之和。如果不…...

rollup环境配置
VUE2.x源码学习笔记 1. rollup环境配置 首先在VScode中新建文件夹vue_sc,然后终端打开定位到打开的文件夹,输入“npm init -y”初始化配置项,运行成功之后文件夹新增package.json文件 继续在终端运行"npm install babel/preset-env ba…...

二分查找与二分答案、递推与递归、双指针、并查集和单调队列
二分查找与二分答案 文章目录二分查找与二分答案应用总结例题木材加工题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示数据规模与约定思路代码递归与递推应用总结[NOIP2003 普及组] 栈题目背景题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示思…...
如何进行域名购买,获取免费ssl证书,使用springboot绑定ssl证书
前言 小编我将用CSDN记录软件开发求学之路上亲身所得与所学的心得与知识,有兴趣的小伙伴可以关注一下!也许一个人独行,可以走的很快,但是一群人结伴而行,才能走的更远!让我们在成长的道路上互相学习&#…...
LabVIEW网络服务安全2
LabVIEW网络服务安全2在客户端应用程序中创建签名对请求进行签名要求您具有能够从客户端的编程语言调用的MD5摘要算法以及SHA256加密摘要算法的实现。这两种算法通常都可用于大多数平台。还需要:1. 要使用的HTTP方法的字符串(“GET”、“POST”、“PUT”…...
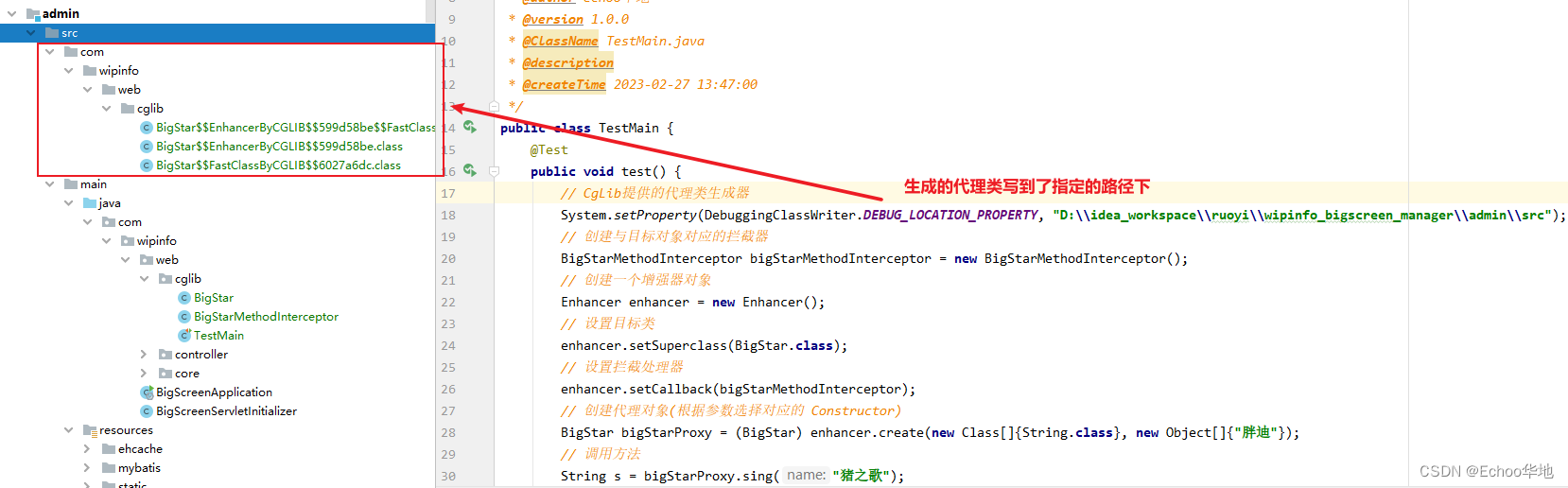
java动态代理
目录儿一、代理模式的作用二、实现代理的方式三、动态代理的实现3.1 jdk动态代理3.2 cglib动态代理一、代理模式的作用 功能增强: 基于某个功能,再增加一些功能。 (比如目标类只负责核心功能,其他附属功能通过代理类完成。代理类的方法名与目…...
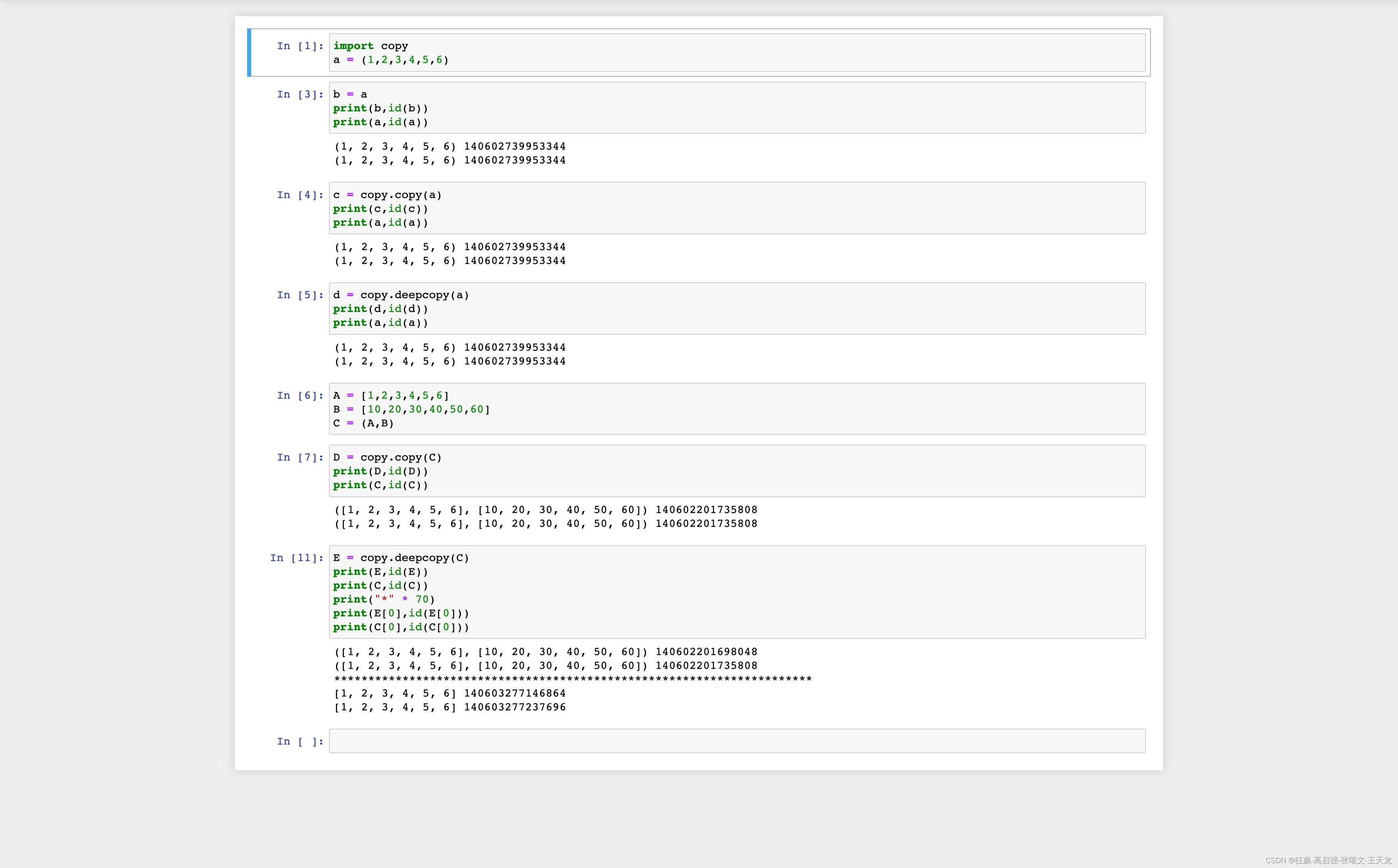
Python 简单可变、复杂可变、简单不可变、复杂不可变类型的copy、deepcopy的行为
copy模块:copy:浅拷贝deepcopy:深拷贝简单可变类型、复杂可变的copy()、deepcopy():简单不可变、复杂不可变类型的copy()、deepcopy():结论:对于简单类型的可变类型copy是深拷贝,改变了该拷贝变…...
QML Item
在QML中所有的可视项目都继承自Item,虽然Item本身没有可视化的外观,但它定义了可视化项目的所有属性。 Item可以作为容器使用: Item{Rectangle{id:retc}Rectangle{id:retc1}Rectangle{id:retc2}Rectangle{id:retc3}} item拥有children属性…...
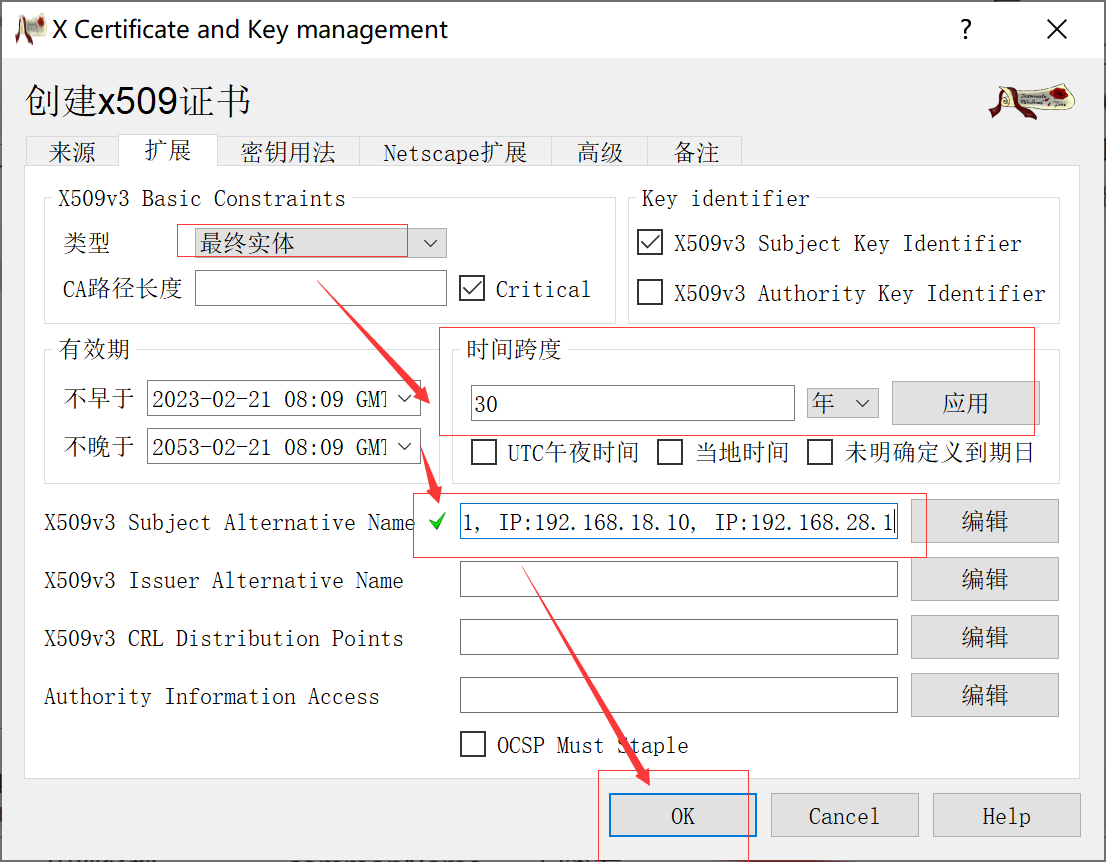
使用xca工具生成自签证书
本文使用 xca 生成自签证书。 概述 之前使用 openssl 生成证书,在 golang 中测试,发现客户端连接失败,经查发现是Subject Alternative Name不支持导致的。因虚拟机 openssl 版本较低,有个功能无法实现,且升级麻烦&…...

Unity IOS 通过命令行导出IPA
新建一个文件然后输入如下内容 #!/usr/bin/env sh /Applications/Unity/Hub/Editor/2020.1.5f1c1/Unity.app/Contents/MacOS/Unity -quit -batchmode -projectPath /Users/zyt/Test -executeMethod Test.BuildEditor.BuildApp cd /Users/zyt/Test/Xcode/unity-xcode xcodebuil…...
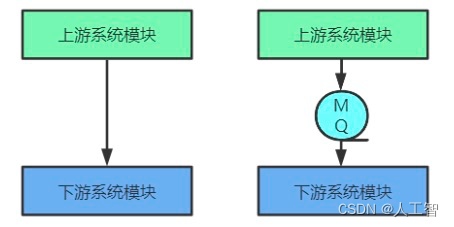
「架构」全链路异步模式
总结自尼恩的全链路异步:网关纯异步化网关层的特点:不需要访问业务数据库只做协议转换和流量转发特点是 IO 密集型,特别适合纯异步的架构,可以极大的节省资源。如何进行网关异步化?使用高性能的通信框架Nettyÿ…...
CleanMyMac4.20最新版新增功能及电脑清理垃圾使用教程
CleanMyMac4.20作为知名的Mac清理工具,仅需一键即可快速而安全地清理系统垃圾,释放磁盘空间,因此一直深受Mac用户的喜爱。在不断更新的版本中,CleanMyMac已经不仅仅满足于只做简单的Mac清理工具,而是为Mac用户提供更多…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

ui框架-文件列表展示
ui框架-文件列表展示 介绍 UI框架的文件列表展示组件,可以展示文件夹,支持列表展示和图标展示模式。组件提供了丰富的功能和可配置选项,适用于文件管理、文件上传等场景。 功能特性 支持列表模式和网格模式的切换展示支持文件和文件夹的层…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...
