跟李沐学AI-深度学习课程05线性代数
线性代数
🏷sec_linear-algebra
在介绍完如何存储和操作数据后,接下来将简要地回顾一下部分基本线性代数内容。
这些内容有助于读者了解和实现本书中介绍的大多数模型。
本节将介绍线性代数中的基本数学对象、算术和运算,并用数学符号和相应的代码实现来表示它们。
标量
如果你曾经在餐厅支付餐费,那么应该已经知道一些基本的线性代数,比如在数字间相加或相乘。
例如,北京的温度为 5 2 ∘ F 52^{\circ}F 52∘F(华氏度,除摄氏度外的另一种温度计量单位)。
严格来说,仅包含一个数值被称为标量(scalar)。
如果要将此华氏度值转换为更常用的摄氏度,
则可以计算表达式 c = 5 9 ( f − 32 ) c=\frac{5}{9}(f-32) c=95(f−32),并将 f f f赋为 52 52 52。
在此等式中,每一项( 5 5 5、 9 9 9和 32 32 32)都是标量值。
符号 c c c和 f f f称为变量(variable),它们表示未知的标量值。
本书采用了数学表示法,其中标量变量由普通小写字母表示(例如, x x x、 y y y和 z z z)。
本书用 R \mathbb{R} R表示所有(连续)实数标量的空间,之后将严格定义空间(space)是什么,
但现在只要记住表达式 x ∈ R x\in\mathbb{R} x∈R是表示 x x x是一个实值标量的正式形式。
符号 ∈ \in ∈称为“属于”,它表示“是集合中的成员”。
例如 x , y ∈ { 0 , 1 } x, y \in \{0,1\} x,y∈{0,1}可以用来表明 x x x和 y y y是值只能为 0 0 0或 1 1 1的数字。
(标量由只有一个元素的张量表示)。
下面的代码将实例化两个标量,并执行一些熟悉的算术运算,即加法、乘法、除法和指数。
from mxnet import np, npx
npx.set_np()x = np.array(3.0)
y = np.array(2.0)x + y, x * y, x / y, x ** y
#@tab pytorch
import torchx = torch.tensor(3.0)
y = torch.tensor(2.0)x + y, x * y, x / y, x**y
#@tab tensorflow
import tensorflow as tfx = tf.constant(3.0)
y = tf.constant(2.0)x + y, x * y, x / y, x**y
#@tab paddle
import warnings
warnings.filterwarnings(action='ignore')
import paddlex = paddle.to_tensor([3.0])
y = paddle.to_tensor([2.0])x + y, x * y, x / y, x**y
向量
[向量可以被视为标量值组成的列表]。
这些标量值被称为向量的元素(element)或分量(component)。
当向量表示数据集中的样本时,它们的值具有一定的现实意义。
例如,如果我们正在训练一个模型来预测贷款违约风险,可能会将每个申请人与一个向量相关联,
其分量与其收入、工作年限、过往违约次数和其他因素相对应。
如果我们正在研究医院患者可能面临的心脏病发作风险,可能会用一个向量来表示每个患者,
其分量为最近的生命体征、胆固醇水平、每天运动时间等。
在数学表示法中,向量通常记为粗体、小写的符号
(例如, x \mathbf{x} x、 y \mathbf{y} y和 z ) \mathbf{z}) z))。
人们通过一维张量表示向量。一般来说,张量可以具有任意长度,取决于机器的内存限制。
x = np.arange(4)
x
#@tab pytorch
x = torch.arange(4)
x
#@tab tensorflow
x = tf.range(4)
x
#@tab paddle
x = paddle.arange(4)
x
我们可以使用下标来引用向量的任一元素,例如可以通过 x i x_i xi来引用第 i i i个元素。
注意,元素 x i x_i xi是一个标量,所以我们在引用它时不会加粗。
大量文献认为列向量是向量的默认方向,在本书中也是如此。
在数学中,向量 x \mathbf{x} x可以写为:
x = [ x 1 x 2 ⋮ x n ] , \mathbf{x} =\begin{bmatrix}x_{1} \\x_{2} \\ \vdots \\x_{n}\end{bmatrix}, x= x1x2⋮xn ,
:eqlabel:eq_vec_def
其中 x 1 , … , x n x_1,\ldots,x_n x1,…,xn是向量的元素。在代码中,我们(通过张量的索引来访问任一元素)。
x[3]
#@tab pytorch
x[3]
#@tab tensorflow
x[3]
#@tab paddle
x[3]
长度、维度和形状
向量只是一个数字数组,就像每个数组都有一个长度一样,每个向量也是如此。
在数学表示法中,如果我们想说一个向量 x \mathbf{x} x由 n n n个实值标量组成,
可以将其表示为 x ∈ R n \mathbf{x}\in\mathbb{R}^n x∈Rn。
向量的长度通常称为向量的维度(dimension)。
与普通的Python数组一样,我们可以通过调用Python的内置len()函数来[访问张量的长度]。
len(x)
#@tab pytorch
len(x)
#@tab tensorflow
len(x)
#@tab paddle
len(x)
当用张量表示一个向量(只有一个轴)时,我们也可以通过.shape属性访问向量的长度。
形状(shape)是一个元素组,列出了张量沿每个轴的长度(维数)。
对于(只有一个轴的张量,形状只有一个元素。)
x.shape
#@tab pytorch
x.shape
#@tab tensorflow
x.shape
#@tab paddle
x.shape
请注意,维度(dimension)这个词在不同上下文时往往会有不同的含义,这经常会使人感到困惑。
为了清楚起见,我们在此明确一下:
向量或轴的维度被用来表示向量或轴的长度,即向量或轴的元素数量。
然而,张量的维度用来表示张量具有的轴数。
在这个意义上,张量的某个轴的维数就是这个轴的长度。
矩阵
正如向量将标量从零阶推广到一阶,矩阵将向量从一阶推广到二阶。
矩阵,我们通常用粗体、大写字母来表示
(例如, X \mathbf{X} X、 Y \mathbf{Y} Y和 Z \mathbf{Z} Z),
在代码中表示为具有两个轴的张量。
数学表示法使用 A ∈ R m × n \mathbf{A} \in \mathbb{R}^{m \times n} A∈Rm×n
来表示矩阵 A \mathbf{A} A,其由 m m m行和 n n n列的实值标量组成。
我们可以将任意矩阵 A ∈ R m × n \mathbf{A} \in \mathbb{R}^{m \times n} A∈Rm×n视为一个表格,
其中每个元素 a i j a_{ij} aij属于第 i i i行第 j j j列:
A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m n ] . \mathbf{A}=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \\ \end{bmatrix}. A= a11a21⋮am1a12a22⋮am2⋯⋯⋱⋯a1na2n⋮amn .
:eqlabel:eq_matrix_def
对于任意 A ∈ R m × n \mathbf{A} \in \mathbb{R}^{m \times n} A∈Rm×n,
A \mathbf{A} A的形状是( m m m, n n n)或 m × n m \times n m×n。
当矩阵具有相同数量的行和列时,其形状将变为正方形;
因此,它被称为方阵(square matrix)。
当调用函数来实例化张量时,
我们可以[通过指定两个分量 m m m和 n n n来创建一个形状为 m × n m \times n m×n的矩阵]。
A = np.arange(20).reshape(5, 4)
A
#@tab pytorch
A = torch.arange(20).reshape(5, 4)
A
#@tab tensorflow
A = tf.reshape(tf.range(20), (5, 4))
A
#@tab paddle
A = paddle.reshape(paddle.arange(20), (5, 4))
A
我们可以通过行索引( i i i)和列索引( j j j)来访问矩阵中的标量元素 a i j a_{ij} aij,
例如 [ A ] i j [\mathbf{A}]_{ij} [A]ij。
如果没有给出矩阵 A \mathbf{A} A的标量元素,如在 :eqref:eq_matrix_def那样,
我们可以简单地使用矩阵 A \mathbf{A} A的小写字母索引下标 a i j a_{ij} aij
来引用 [ A ] i j [\mathbf{A}]_{ij} [A]ij。
为了表示起来简单,只有在必要时才会将逗号插入到单独的索引中,
例如 a 2 , 3 j a_{2,3j} a2,3j和 [ A ] 2 i − 1 , 3 [\mathbf{A}]_{2i-1,3} [A]2i−1,3。
当我们交换矩阵的行和列时,结果称为矩阵的转置(transpose)。
通常用 a ⊤ \mathbf{a}^\top a⊤来表示矩阵的转置,如果 B = A ⊤ \mathbf{B}=\mathbf{A}^\top B=A⊤,
则对于任意 i i i和 j j j,都有 b i j = a j i b_{ij}=a_{ji} bij=aji。
因此,在 :eqref:eq_matrix_def中的转置是一个形状为 n × m n \times m n×m的矩阵:
A ⊤ = [ a 11 a 21 … a m 1 a 12 a 22 … a m 2 ⋮ ⋮ ⋱ ⋮ a 1 n a 2 n … a m n ] . \mathbf{A}^\top = \begin{bmatrix} a_{11} & a_{21} & \dots & a_{m1} \\ a_{12} & a_{22} & \dots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \dots & a_{mn} \end{bmatrix}. A⊤= a11a12⋮a1na21a22⋮a2n……⋱…am1am2⋮amn .
现在在代码中访问(矩阵的转置)。
A.T
#@tab pytorch
A.T
#@tab tensorflow
tf.transpose(A)
#@tab paddle
paddle.transpose(A, perm=[1, 0])
作为方阵的一种特殊类型,[对称矩阵(symmetric matrix) A \mathbf{A} A等于其转置: A = A ⊤ \mathbf{A} = \mathbf{A}^\top A=A⊤]。
这里定义一个对称矩阵 B \mathbf{B} B:
B = np.array([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B
#@tab pytorch
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B
#@tab tensorflow
B = tf.constant([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B
#@tab paddle
B = paddle.to_tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B
现在我们将B与它的转置进行比较。
B == B.T
#@tab pytorch
B == B.T
#@tab tensorflow
B == tf.transpose(B)
#@tab paddle
B == paddle.transpose(B, perm=[1, 0])
矩阵是有用的数据结构:它们允许我们组织具有不同模式的数据。
例如,我们矩阵中的行可能对应于不同的房屋(数据样本),而列可能对应于不同的属性。
曾经使用过电子表格软件或已阅读过 :numref:sec_pandas的人,应该对此很熟悉。
因此,尽管单个向量的默认方向是列向量,但在表示表格数据集的矩阵中,
将每个数据样本作为矩阵中的行向量更为常见。
后面的章节将讲到这点,这种约定将支持常见的深度学习实践。
例如,沿着张量的最外轴,我们可以访问或遍历小批量的数据样本。
张量
[就像向量是标量的推广,矩阵是向量的推广一样,我们可以构建具有更多轴的数据结构]。
张量(本小节中的“张量”指代数对象)是描述具有任意数量轴的 n n n维数组的通用方法。
例如,向量是一阶张量,矩阵是二阶张量。
张量用特殊字体的大写字母表示(例如, X \mathsf{X} X、 Y \mathsf{Y} Y和 Z \mathsf{Z} Z),
它们的索引机制(例如 x i j k x_{ijk} xijk和 [ X ] 1 , 2 i − 1 , 3 [\mathsf{X}]_{1,2i-1,3} [X]1,2i−1,3)与矩阵类似。
当我们开始处理图像时,张量将变得更加重要,图像以 n n n维数组形式出现,
其中3个轴对应于高度、宽度,以及一个通道(channel)轴,
用于表示颜色通道(红色、绿色和蓝色)。
现在先将高阶张量暂放一边,而是专注学习其基础知识。
X = np.arange(24).reshape(2, 3, 4)
X
#@tab pytorch
X = torch.arange(24).reshape(2, 3, 4)
X
#@tab tensorflow
X = tf.reshape(tf.range(24), (2, 3, 4))
X
#@tab paddle
X = paddle.reshape(paddle.arange(24), (2, 3, 4))
X
张量算法的基本性质
标量、向量、矩阵和任意数量轴的张量(本小节中的“张量”指代数对象)有一些实用的属性。
例如,从按元素操作的定义中可以注意到,任何按元素的一元运算都不会改变其操作数的形状。
同样,[给定具有相同形状的任意两个张量,任何按元素二元运算的结果都将是相同形状的张量]。
例如,将两个相同形状的矩阵相加,会在这两个矩阵上执行元素加法。
A = np.arange(20).reshape(5, 4)
B = A.copy() # 通过分配新内存,将A的一个副本分配给B
A, A + B
#@tab pytorch
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 通过分配新内存,将A的一个副本分配给B
A, A + B
#@tab tensorflow
A = tf.reshape(tf.range(20, dtype=tf.float32), (5, 4))
B = A # 不能通过分配新内存将A克隆到B
A, A + B
#@tab paddle
A = paddle.reshape(paddle.arange(20, dtype=paddle.float32), (5, 4))
B = A.clone() # 通过分配新内存,将A的一个副本分配给B
A, A + B
具体而言,[两个矩阵的按元素乘法称为Hadamard积(Hadamard product)(数学符号 ⊙ \odot ⊙)]。
对于矩阵 B ∈ R m × n \mathbf{B} \in \mathbb{R}^{m \times n} B∈Rm×n,
其中第 i i i行和第 j j j列的元素是 b i j b_{ij} bij。
矩阵 A \mathbf{A} A(在 :eqref:eq_matrix_def中定义)和 B \mathbf{B} B的Hadamard积为:
A ⊙ B = [ a 11 b 11 a 12 b 12 … a 1 n b 1 n a 21 b 21 a 22 b 22 … a 2 n b 2 n ⋮ ⋮ ⋱ ⋮ a m 1 b m 1 a m 2 b m 2 … a m n b m n ] . \mathbf{A} \odot \mathbf{B} = \begin{bmatrix} a_{11} b_{11} & a_{12} b_{12} & \dots & a_{1n} b_{1n} \\ a_{21} b_{21} & a_{22} b_{22} & \dots & a_{2n} b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} b_{m1} & a_{m2} b_{m2} & \dots & a_{mn} b_{mn} \end{bmatrix}. A⊙B= a11b11a21b21⋮am1bm1a12b12a22b22⋮am2bm2……⋱…a1nb1na2nb2n⋮amnbmn .
A * B
#@tab pytorch
A * B
#@tab tensorflow
A * B
#@tab paddle
A * B
将张量乘以或加上一个标量不会改变张量的形状,其中张量的每个元素都将与标量相加或相乘。
a = 2
X = np.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape
#@tab pytorch
a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape
#@tab tensorflow
a = 2
X = tf.reshape(tf.range(24), (2, 3, 4))
a + X, (a * X).shape
#@tab paddle
a = 2
X = paddle.reshape(paddle.arange(24), (2, 3, 4))
a + X, (a * X).shape
降维
🏷subseq_lin-alg-reduction
我们可以对任意张量进行的一个有用的操作是[计算其元素的和]。
数学表示法使用 ∑ \sum ∑符号表示求和。
为了表示长度为 d d d的向量中元素的总和,可以记为 ∑ i = 1 d x i \sum_{i=1}^dx_i ∑i=1dxi。
在代码中可以调用计算求和的函数:
x = np.arange(4)
x, x.sum()
#@tab pytorch
x = torch.arange(4, dtype=torch.float32)
x, x.sum()
#@tab tensorflow
x = tf.range(4, dtype=tf.float32)
x, tf.reduce_sum(x)
#@tab paddle
x = paddle.arange(4, dtype=paddle.float32)
x, x.sum()
我们可以(表示任意形状张量的元素和)。
例如,矩阵 A \mathbf{A} A中元素的和可以记为 ∑ i = 1 m ∑ j = 1 n a i j \sum_{i=1}^{m} \sum_{j=1}^{n} a_{ij} ∑i=1m∑j=1naij。
A.shape, A.sum()
#@tab pytorch
A.shape, A.sum()
#@tab tensorflow
A.shape, tf.reduce_sum(A)
#@tab paddle
A.shape, A.sum()
默认情况下,调用求和函数会沿所有的轴降低张量的维度,使它变为一个标量。
我们还可以[指定张量沿哪一个轴来通过求和降低维度]。
以矩阵为例,为了通过求和所有行的元素来降维(轴0),可以在调用函数时指定axis=0。
由于输入矩阵沿0轴降维以生成输出向量,因此输入轴0的维数在输出形状中消失。
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
#@tab pytorch
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
#@tab tensorflow
A_sum_axis0 = tf.reduce_sum(A, axis=0)
A_sum_axis0, A_sum_axis0.shape
#@tab paddle
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
指定axis=1将通过汇总所有列的元素降维(轴1)。因此,输入轴1的维数在输出形状中消失。
A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
#@tab pytorch
A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
#@tab tensorflow
A_sum_axis1 = tf.reduce_sum(A, axis=1)
A_sum_axis1, A_sum_axis1.shape
#@tab paddle
A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
沿着行和列对矩阵求和,等价于对矩阵的所有元素进行求和。
A.sum(axis=[0, 1]) # 结果和A.sum()相同
#@tab pytorch
A.sum(axis=[0, 1]) # 结果和A.sum()相同
#@tab tensorflow
tf.reduce_sum(A, axis=[0, 1]) # 结果和tf.reduce_sum(A)相同
#@tab paddle
A.sum(axis=[0, 1])
[一个与求和相关的量是平均值(mean或average)]。
我们通过将总和除以元素总数来计算平均值。
在代码中,我们可以调用函数来计算任意形状张量的平均值。
A.mean(), A.sum() / A.size
#@tab pytorch
A.mean(), A.sum() / A.numel()
#@tab tensorflow
tf.reduce_mean(A), tf.reduce_sum(A) / tf.size(A).numpy()
#@tab paddle
A.mean(), A.sum() / A.numel()
同样,计算平均值的函数也可以沿指定轴降低张量的维度。
A.mean(axis=0), A.sum(axis=0) / A.shape[0]
#@tab pytorch
A.mean(axis=0), A.sum(axis=0) / A.shape[0]
#@tab tensorflow
tf.reduce_mean(A, axis=0), tf.reduce_sum(A, axis=0) / A.shape[0]
#@tab paddle
A.mean(axis=0), A.sum(axis=0) / A.shape[0]
非降维求和
🏷subseq_lin-alg-non-reduction
但是,有时在调用函数来[计算总和或均值时保持轴数不变]会很有用。
sum_A = A.sum(axis=1, keepdims=True)
sum_A
#@tab pytorch
sum_A = A.sum(axis=1, keepdims=True)
sum_A
#@tab tensorflow
sum_A = tf.reduce_sum(A, axis=1, keepdims=True)
sum_A
#@tab paddle
sum_A = paddle.sum(A, axis=1, keepdim=True)
sum_A
例如,由于sum_A在对每行进行求和后仍保持两个轴,我们可以(通过广播将A除以sum_A)。
A / sum_A
#@tab pytorch
A / sum_A
#@tab tensorflow
A / sum_A
#@tab paddle
A / sum_A
如果我们想沿[某个轴计算A元素的累积总和],
比如axis=0(按行计算),可以调用cumsum函数。
此函数不会沿任何轴降低输入张量的维度。
A.cumsum(axis=0)
#@tab pytorch
A.cumsum(axis=0)
#@tab tensorflow
tf.cumsum(A, axis=0)
#@tab paddle
A.cumsum(axis=0)
点积(Dot Product)
我们已经学习了按元素操作、求和及平均值。
另一个最基本的操作之一是点积。
给定两个向量 x , y ∈ R d \mathbf{x},\mathbf{y}\in\mathbb{R}^d x,y∈Rd,
它们的点积(dot product) x ⊤ y \mathbf{x}^\top\mathbf{y} x⊤y
(或 ⟨ x , y ⟩ \langle\mathbf{x},\mathbf{y}\rangle ⟨x,y⟩)
是相同位置的按元素乘积的和: x ⊤ y = ∑ i = 1 d x i y i \mathbf{x}^\top \mathbf{y} = \sum_{i=1}^{d} x_i y_i x⊤y=∑i=1dxiyi。
[点积是相同位置的按元素乘积的和]
y = np.ones(4)
x, y, np.dot(x, y)
#@tab pytorch
y = torch.ones(4, dtype = torch.float32)
x, y, torch.dot(x, y)
#@tab tensorflow
y = tf.ones(4, dtype=tf.float32)
x, y, tf.tensordot(x, y, axes=1)
#@tab paddle
y = paddle.ones(shape=[4], dtype='float32')
x, y, paddle.dot(x, y)
注意,(我们可以通过执行按元素乘法,然后进行求和来表示两个向量的点积):
np.sum(x * y)
#@tab pytorch
torch.sum(x * y)
#@tab tensorflow
tf.reduce_sum(x * y)
#@tab paddle
paddle.sum(x * y)
点积在很多场合都很有用。
例如,给定一组由向量 x ∈ R d \mathbf{x} \in \mathbb{R}^d x∈Rd表示的值,
和一组由 w ∈ R d \mathbf{w} \in \mathbb{R}^d w∈Rd表示的权重。
x \mathbf{x} x中的值根据权重 w \mathbf{w} w的加权和,
可以表示为点积 x ⊤ w \mathbf{x}^\top \mathbf{w} x⊤w。
当权重为非负数且和为1(即 ( ∑ i = 1 d w i = 1 ) \left(\sum_{i=1}^{d}{w_i}=1\right) (∑i=1dwi=1))时,
点积表示加权平均(weighted average)。
将两个向量规范化得到单位长度后,点积表示它们夹角的余弦。
本节后面的内容将正式介绍长度(length)的概念。
矩阵-向量积
现在我们知道如何计算点积,可以开始理解矩阵-向量积(matrix-vector product)。
回顾分别在 :eqref:eq_matrix_def和 :eqref:eq_vec_def中定义的矩阵 A ∈ R m × n \mathbf{A} \in \mathbb{R}^{m \times n} A∈Rm×n和向量 x ∈ R n \mathbf{x} \in \mathbb{R}^n x∈Rn。
让我们将矩阵 A \mathbf{A} A用它的行向量表示:
A = [ a 1 ⊤ a 2 ⊤ ⋮ a m ⊤ ] , \mathbf{A}= \begin{bmatrix} \mathbf{a}^\top_{1} \\ \mathbf{a}^\top_{2} \\ \vdots \\ \mathbf{a}^\top_m \\ \end{bmatrix}, A= a1⊤a2⊤⋮am⊤ ,
其中每个 a i ⊤ ∈ R n \mathbf{a}^\top_{i} \in \mathbb{R}^n ai⊤∈Rn都是行向量,表示矩阵的第 i i i行。
[矩阵向量积 A x \mathbf{A}\mathbf{x} Ax是一个长度为 m m m的列向量,
其第 i i i个元素是点积 a i ⊤ x \mathbf{a}^\top_i \mathbf{x} ai⊤x]:
A x = [ a 1 ⊤ a 2 ⊤ ⋮ a m ⊤ ] x = [ a 1 ⊤ x a 2 ⊤ x ⋮ a m ⊤ x ] . \mathbf{A}\mathbf{x} = \begin{bmatrix} \mathbf{a}^\top_{1} \\ \mathbf{a}^\top_{2} \\ \vdots \\ \mathbf{a}^\top_m \\ \end{bmatrix}\mathbf{x} = \begin{bmatrix} \mathbf{a}^\top_{1} \mathbf{x} \\ \mathbf{a}^\top_{2} \mathbf{x} \\ \vdots\\ \mathbf{a}^\top_{m} \mathbf{x}\\ \end{bmatrix}. Ax= a1⊤a2⊤⋮am⊤ x= a1⊤xa2⊤x⋮am⊤x .
我们可以把一个矩阵 A ∈ R m × n \mathbf{A} \in \mathbb{R}^{m \times n} A∈Rm×n乘法看作一个从 R n \mathbb{R}^{n} Rn到 R m \mathbb{R}^{m} Rm向量的转换。
这些转换是非常有用的,例如可以用方阵的乘法来表示旋转。
后续章节将讲到,我们也可以使用矩阵-向量积来描述在给定前一层的值时,
求解神经网络每一层所需的复杂计算。
:begin_tab:mxnet
在代码中使用张量表示矩阵-向量积,我们使用与点积相同的dot函数。
当我们为矩阵A和向量x调用np.dot(A,x)时,会执行矩阵-向量积。
注意,A的列维数(沿轴1的长度)必须与x的维数(其长度)相同。
:end_tab:
:begin_tab:pytorch
在代码中使用张量表示矩阵-向量积,我们使用mv函数。
当我们为矩阵A和向量x调用torch.mv(A, x)时,会执行矩阵-向量积。
注意,A的列维数(沿轴1的长度)必须与x的维数(其长度)相同。
:end_tab:
:begin_tab:tensorflow
在代码中使用张量表示矩阵-向量积,我们使用与点积相同的matvec函数。
当我们为矩阵A和向量x调用tf.linalg.matvec(A, x)时,会执行矩阵-向量积。
注意,A的列维数(沿轴1的长度)必须与x的维数(其长度)相同。
:end_tab:
A.shape, x.shape, np.dot(A, x)
#@tab pytorch
A.shape, x.shape, torch.mv(A, x)
#@tab tensorflow
A.shape, x.shape, tf.linalg.matvec(A, x)
#@tab paddle
A.shape, x.shape, paddle.mv(A, x)
矩阵-矩阵乘法
在掌握点积和矩阵-向量积的知识后,
那么矩阵-矩阵乘法(matrix-matrix multiplication)应该很简单。
假设有两个矩阵 A ∈ R n × k \mathbf{A} \in \mathbb{R}^{n \times k} A∈Rn×k和 B ∈ R k × m \mathbf{B} \in \mathbb{R}^{k \times m} B∈Rk×m:
A = [ a 11 a 12 ⋯ a 1 k a 21 a 22 ⋯ a 2 k ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n k ] , B = [ b 11 b 12 ⋯ b 1 m b 21 b 22 ⋯ b 2 m ⋮ ⋮ ⋱ ⋮ b k 1 b k 2 ⋯ b k m ] . \mathbf{A}=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1k} \\ a_{21} & a_{22} & \cdots & a_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nk} \\ \end{bmatrix},\quad \mathbf{B}=\begin{bmatrix} b_{11} & b_{12} & \cdots & b_{1m} \\ b_{21} & b_{22} & \cdots & b_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ b_{k1} & b_{k2} & \cdots & b_{km} \\ \end{bmatrix}. A= a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1ka2k⋮ank ,B= b11b21⋮bk1b12b22⋮bk2⋯⋯⋱⋯b1mb2m⋮bkm .
用行向量 a i ⊤ ∈ R k \mathbf{a}^\top_{i} \in \mathbb{R}^k ai⊤∈Rk表示矩阵 A \mathbf{A} A的第 i i i行,并让列向量 b j ∈ R k \mathbf{b}_{j} \in \mathbb{R}^k bj∈Rk作为矩阵 B \mathbf{B} B的第 j j j列。要生成矩阵积 C = A B \mathbf{C} = \mathbf{A}\mathbf{B} C=AB,最简单的方法是考虑 A \mathbf{A} A的行向量和 B \mathbf{B} B的列向量:
A = [ a 1 ⊤ a 2 ⊤ ⋮ a n ⊤ ] , B = [ b 1 b 2 ⋯ b m ] . \mathbf{A}= \begin{bmatrix} \mathbf{a}^\top_{1} \\ \mathbf{a}^\top_{2} \\ \vdots \\ \mathbf{a}^\top_n \\ \end{bmatrix}, \quad \mathbf{B}=\begin{bmatrix} \mathbf{b}_{1} & \mathbf{b}_{2} & \cdots & \mathbf{b}_{m} \\ \end{bmatrix}. A= a1⊤a2⊤⋮an⊤ ,B=[b1b2⋯bm].
当我们简单地将每个元素 c i j c_{ij} cij计算为点积 a i ⊤ b j \mathbf{a}^\top_i \mathbf{b}_j ai⊤bj:
C = A B = [ a 1 ⊤ a 2 ⊤ ⋮ a n ⊤ ] [ b 1 b 2 ⋯ b m ] = [ a 1 ⊤ b 1 a 1 ⊤ b 2 ⋯ a 1 ⊤ b m a 2 ⊤ b 1 a 2 ⊤ b 2 ⋯ a 2 ⊤ b m ⋮ ⋮ ⋱ ⋮ a n ⊤ b 1 a n ⊤ b 2 ⋯ a n ⊤ b m ] . \mathbf{C} = \mathbf{AB} = \begin{bmatrix} \mathbf{a}^\top_{1} \\ \mathbf{a}^\top_{2} \\ \vdots \\ \mathbf{a}^\top_n \\ \end{bmatrix} \begin{bmatrix} \mathbf{b}_{1} & \mathbf{b}_{2} & \cdots & \mathbf{b}_{m} \\ \end{bmatrix} = \begin{bmatrix} \mathbf{a}^\top_{1} \mathbf{b}_1 & \mathbf{a}^\top_{1}\mathbf{b}_2& \cdots & \mathbf{a}^\top_{1} \mathbf{b}_m \\ \mathbf{a}^\top_{2}\mathbf{b}_1 & \mathbf{a}^\top_{2} \mathbf{b}_2 & \cdots & \mathbf{a}^\top_{2} \mathbf{b}_m \\ \vdots & \vdots & \ddots &\vdots\\ \mathbf{a}^\top_{n} \mathbf{b}_1 & \mathbf{a}^\top_{n}\mathbf{b}_2& \cdots& \mathbf{a}^\top_{n} \mathbf{b}_m \end{bmatrix}. C=AB= a1⊤a2⊤⋮an⊤ [b1b2⋯bm]= a1⊤b1a2⊤b1⋮an⊤b1a1⊤b2a2⊤b2⋮an⊤b2⋯⋯⋱⋯a1⊤bma2⊤bm⋮an⊤bm .
[我们可以将矩阵-矩阵乘法 A B \mathbf{AB} AB看作简单地执行 m m m次矩阵-向量积,并将结果拼接在一起,形成一个 n × m n \times m n×m矩阵]。
在下面的代码中,我们在A和B上执行矩阵乘法。
这里的A是一个5行4列的矩阵,B是一个4行3列的矩阵。
两者相乘后,我们得到了一个5行3列的矩阵。
B = np.ones(shape=(4, 3))
np.dot(A, B)
#@tab pytorch
B = torch.ones(4, 3)
torch.mm(A, B)
#@tab tensorflow
B = tf.ones((4, 3), tf.float32)
tf.matmul(A, B)
#@tab paddle
B = paddle.ones(shape=[4, 3], dtype='float32')
paddle.mm(A, B)
矩阵-矩阵乘法可以简单地称为矩阵乘法,不应与"Hadamard积"混淆。
范数
🏷subsec_lin-algebra-norms
线性代数中最有用的一些运算符是范数(norm)。
非正式地说,向量的范数是表示一个向量有多大。
这里考虑的大小(size)概念不涉及维度,而是分量的大小。
在线性代数中,向量范数是将向量映射到标量的函数 f f f。
给定任意向量 x \mathbf{x} x,向量范数要满足一些属性。
第一个性质是:如果我们按常数因子 α \alpha α缩放向量的所有元素,
其范数也会按相同常数因子的绝对值缩放:
f ( α x ) = ∣ α ∣ f ( x ) . f(\alpha \mathbf{x}) = |\alpha| f(\mathbf{x}). f(αx)=∣α∣f(x).
第二个性质是熟悉的三角不等式:
f ( x + y ) ≤ f ( x ) + f ( y ) . f(\mathbf{x} + \mathbf{y}) \leq f(\mathbf{x}) + f(\mathbf{y}). f(x+y)≤f(x)+f(y).
第三个性质简单地说范数必须是非负的:
f ( x ) ≥ 0. f(\mathbf{x}) \geq 0. f(x)≥0.
这是有道理的。因为在大多数情况下,任何东西的最小的大小是0。
最后一个性质要求范数最小为0,当且仅当向量全由0组成。
∀ i , [ x ] i = 0 ⇔ f ( x ) = 0. \forall i, [\mathbf{x}]_i = 0 \Leftrightarrow f(\mathbf{x})=0. ∀i,[x]i=0⇔f(x)=0.
范数听起来很像距离的度量。
欧几里得距离和毕达哥拉斯定理中的非负性概念和三角不等式可能会给出一些启发。
事实上,欧几里得距离是一个 L 2 L_2 L2范数:
假设 n n n维向量 x \mathbf{x} x中的元素是 x 1 , … , x n x_1,\ldots,x_n x1,…,xn,其[ L 2 L_2 L2范数是向量元素平方和的平方根:]
( ∥ x ∥ 2 = ∑ i = 1 n x i 2 , \|\mathbf{x}\|_2 = \sqrt{\sum_{i=1}^n x_i^2}, ∥x∥2=i=1∑nxi2,)
其中,在 L 2 L_2 L2范数中常常省略下标 2 2 2,也就是说 ∥ x ∥ \|\mathbf{x}\| ∥x∥等同于 ∥ x ∥ 2 \|\mathbf{x}\|_2 ∥x∥2。
在代码中,我们可以按如下方式计算向量的 L 2 L_2 L2范数。
u = np.array([3, -4])
np.linalg.norm(u)
#@tab pytorch
u = torch.tensor([3.0, -4.0])
torch.norm(u)
#@tab tensorflow
u = tf.constant([3.0, -4.0])
tf.norm(u)
#@tab paddle
u = paddle.to_tensor([3.0, -4.0])
paddle.norm(u)
深度学习中更经常地使用 L 2 L_2 L2范数的平方,也会经常遇到[ L 1 L_1 L1范数,它表示为向量元素的绝对值之和:]
( ∥ x ∥ 1 = ∑ i = 1 n ∣ x i ∣ . \|\mathbf{x}\|_1 = \sum_{i=1}^n \left|x_i \right|. ∥x∥1=i=1∑n∣xi∣.)
与 L 2 L_2 L2范数相比, L 1 L_1 L1范数受异常值的影响较小。
为了计算 L 1 L_1 L1范数,我们将绝对值函数和按元素求和组合起来。
np.abs(u).sum()
#@tab pytorch
torch.abs(u).sum()
#@tab tensorflow
tf.reduce_sum(tf.abs(u))
#@tab paddle
paddle.abs(u).sum()
L 2 L_2 L2范数和 L 1 L_1 L1范数都是更一般的 L p L_p Lp范数的特例:
∥ x ∥ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 / p . \|\mathbf{x}\|_p = \left(\sum_{i=1}^n \left|x_i \right|^p \right)^{1/p}. ∥x∥p=(i=1∑n∣xi∣p)1/p.
类似于向量的 L 2 L_2 L2范数,[矩阵] X ∈ R m × n \mathbf{X} \in \mathbb{R}^{m \times n} X∈Rm×n(的Frobenius范数(Frobenius norm)是矩阵元素平方和的平方根:)
( ∥ X ∥ F = ∑ i = 1 m ∑ j = 1 n x i j 2 . \|\mathbf{X}\|_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n x_{ij}^2}. ∥X∥F=i=1∑mj=1∑nxij2.)
Frobenius范数满足向量范数的所有性质,它就像是矩阵形向量的 L 2 L_2 L2范数。
调用以下函数将计算矩阵的Frobenius范数。
np.linalg.norm(np.ones((4, 9)))
#@tab pytorch
torch.norm(torch.ones((4, 9)))
#@tab tensorflow
tf.norm(tf.ones((4, 9)))
#@tab paddle
paddle.norm(paddle.ones(shape=[4, 9], dtype='float32'))
范数和目标
🏷subsec_norms_and_objectives
在深度学习中,我们经常试图解决优化问题:
最大化分配给观测数据的概率;
最小化预测和真实观测之间的距离。
用向量表示物品(如单词、产品或新闻文章),以便最小化相似项目之间的距离,最大化不同项目之间的距离。
目标,或许是深度学习算法最重要的组成部分(除了数据),通常被表达为范数。
关于线性代数的更多信息
仅用一节,我们就教会了阅读本书所需的、用以理解现代深度学习的线性代数。
线性代数还有很多,其中很多数学对于机器学习非常有用。
例如,矩阵可以分解为因子,这些分解可以显示真实世界数据集中的低维结构。
机器学习的整个子领域都侧重于使用矩阵分解及其向高阶张量的泛化,来发现数据集中的结构并解决预测问题。
当开始动手尝试并在真实数据集上应用了有效的机器学习模型,你会更倾向于学习更多数学。
因此,这一节到此结束,本书将在后面介绍更多数学知识。
如果渴望了解有关线性代数的更多信息,可以参考线性代数运算的在线附录或其他优秀资源 :cite:Strang.1993,Kolter.2008,Petersen.Pedersen.ea.2008。
小结
- 标量、向量、矩阵和张量是线性代数中的基本数学对象。
- 向量泛化自标量,矩阵泛化自向量。
- 标量、向量、矩阵和张量分别具有零、一、二和任意数量的轴。
- 一个张量可以通过
sum和mean沿指定的轴降低维度。 - 两个矩阵的按元素乘法被称为他们的Hadamard积。它与矩阵乘法不同。
- 在深度学习中,我们经常使用范数,如 L 1 L_1 L1范数、 L 2 L_2 L2范数和Frobenius范数。
- 我们可以对标量、向量、矩阵和张量执行各种操作。
练习
- 证明一个矩阵 A \mathbf{A} A的转置的转置是 A \mathbf{A} A,即 ( A ⊤ ) ⊤ = A (\mathbf{A}^\top)^\top = \mathbf{A} (A⊤)⊤=A。
- 给出两个矩阵 A \mathbf{A} A和 B \mathbf{B} B,证明“它们转置的和”等于“它们和的转置”,即 A ⊤ + B ⊤ = ( A + B ) ⊤ \mathbf{A}^\top + \mathbf{B}^\top = (\mathbf{A} + \mathbf{B})^\top A⊤+B⊤=(A+B)⊤。
- 给定任意方阵 A \mathbf{A} A, A + A ⊤ \mathbf{A} + \mathbf{A}^\top A+A⊤总是对称的吗?为什么?
- 本节中定义了形状 ( 2 , 3 , 4 ) (2,3,4) (2,3,4)的张量
X。len(X)的输出结果是什么? - 对于任意形状的张量
X,len(X)是否总是对应于X特定轴的长度?这个轴是什么? - 运行
A/A.sum(axis=1),看看会发生什么。请分析一下原因? - 考虑一个具有形状 ( 2 , 3 , 4 ) (2,3,4) (2,3,4)的张量,在轴0、1、2上的求和输出是什么形状?
- 为
linalg.norm函数提供3个或更多轴的张量,并观察其输出。对于任意形状的张量这个函数计算得到什么?
:begin_tab:mxnet
Discussions
:end_tab:
:begin_tab:pytorch
Discussions
:end_tab:
:begin_tab:tensorflow
Discussions
:end_tab:
:begin_tab:paddle
Discussions
:end_tab:
相关文章:

跟李沐学AI-深度学习课程05线性代数
线性代数 🏷sec_linear-algebra 在介绍完如何存储和操作数据后,接下来将简要地回顾一下部分基本线性代数内容。 这些内容有助于读者了解和实现本书中介绍的大多数模型。 本节将介绍线性代数中的基本数学对象、算术和运算,并用数学符号和相应…...
电子病历编辑器源码(Springboot+原生HTML)
一、系统简介 本系统主要面向医院医生、护士,提供对住院病人的电子病历书写、保存、修改、打印等功能。本系统基于云端SaaS服务方式,通过浏览器方式访问和使用系统功能,提供电子病历在线制作、管理和使用的一体化电子病历解决方案,…...

Qt的日志输出
在Qt中,一般习惯使用qDebug信息进行输出和打印调试信息到console或者文件中,在qDebug中,也有一些小技巧,可以帮助我们更好的使用qDebug打印日志记录,本文分享了qDebug使用的一些小技巧。 1. 打印出文件名、行号、调用函…...

基于热交换算法优化概率神经网络PNN的分类预测 - 附代码
基于热交换算法优化概率神经网络PNN的分类预测 - 附代码 文章目录 基于热交换算法优化概率神经网络PNN的分类预测 - 附代码1.PNN网络概述2.变压器故障诊街系统相关背景2.1 模型建立 3.基于热交换优化的PNN网络5.测试结果6.参考文献7.Matlab代码 摘要:针对PNN神经网络…...

main.js 中的 render函数
按照之前的单组件文件中的写法,我们的写法应该是这样的 import App from ./App.vuenew Vue({el: #app,templete: <App></App>,components: {App}, }) 1、定义el根节点。2、注册App组件。3、渲染 templete 模板 但是在脚手架工程中,他是这…...
Pandas 将DataFrame中单元格内的列表拆分成单独的行
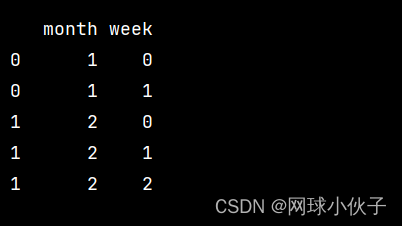
使用 explode 函数 import pandas as pddata {month: [1, 2],week: [[i for i in range(2)], [i for i in range(3)]]} df pd.DataFrame(data) print(df)df df.explode(week) print(df)...

PDF转化为图片
Java 类 PDF2Image 在包 com.oncloudsoft.zbznhc.common.util.pdf 中是用来将 PDF 文件转换为图像的。它使用了 Apache PDFBox 库来处理 PDF 文档并生成图像。下面是类中每个部分的详细解释: 类和方法说明 类 PDF2Image: 使用了 Lombok 库的 Slf4j 注解,…...
【Java】智慧工地管理系统源码(SaaS模式)
智慧工地是聚焦工程施工现场,紧紧围绕人、机、料、法、环等关键要素,综合运用物联网、云计算、大数据、移动计算和智能设备等软硬件信息技术,与施工生产过程相融合。 一、什么是智慧工地 智慧工地是指利用移动互联、物联网、智能算法、地理信…...
torch.nn.functional.log_softmax 函数解析
该函数将输出向量转化为概率分布,作用和softmax一致。 相比softmax,对较小的概率分布处理能力更好。 一、定义 softmax 计算公式: log_softmax 计算公式: 可见仅仅是将 softmax 最外层套上 log 函数。 二、使用场景 log_soft…...

jQuery、vue、小程序、uni-app中的本地存储数据和接受数据是什么?
在这四个工具/框架中,Uni-app和微信小程序比较类似,因为它们都是为了实现跨平台开发而设计的。 jQuery 是一个快速、小巧且特性丰富的 JavaScript 库。它提供了各种操作和处理 HTML DOM、事件、动画,以及提供各种工具函数的功能。然而&#…...

黑马React18: 基础Part 1
黑马React: 基础1 Date: November 15, 2023 Sum: React介绍、JSX、事件绑定、组件、useState、B站评论 React介绍 概念: React由Meta公司研发,是一个用于 构建Web和原生交互界面的库 优势: 1-组件化的开发方式 2-优秀的性能 3-丰富的生态 4-跨平台开发 开发环境搭…...
windows Oracle Database 19c 卸载教程
目录 打开任务管理器 停止数据库服务 Universal Installer 卸载Oracle数据库程序 使用Oracle Installer卸载 删除注册表项 重新启动系统 打开任务管理器 ctrlShiftEsc可以快速打开任务管理器,找到oracle所有服务然后停止。 停止数据库服务 在开始卸载之前&a…...
)
动态规划解决leetcode上的两道回文问题(针对思路)
本期主讲的是使用动态规划去解决两道回文问题,分别是 647. 回文子串 - 力扣(LeetCode) 516. 最长回文子序列 - 力扣(LeetCode) 而不是leetcode5.最长回文子串,虽然这道题也是回文问题,也可以…...

使用人工智能自动测试 Flutter 应用程序
移动应用程序开发的增长速度比以往任何时候都快。几乎每个企业都需要移动应用程序来保持市场竞争力。由于像 React Native 这样的跨平台移动应用程序开发框架允许公司使用单一源代码和单一编程语言构建 iOS 和 Android 应用程序, Flutter是 Google 支持的另一个热门…...
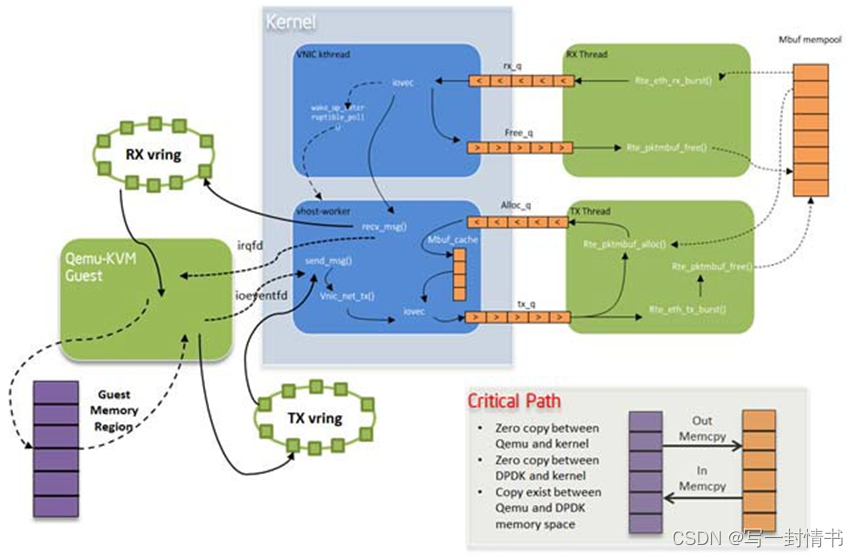
四、程序员指南:数据平面开发套件
REORDER LIBRARY 重排序库提供了根据其序列号对mbuf进行重排序的机制。 16.1 操作 重排序库本质上是一个对mbuf进行重新排序的缓冲区。用户将乱序的mbuf插入重排序缓冲区,并从中提取顺序正确的mbuf。 在任何给定时刻,重排序缓冲区包含其序列号位于序列…...

Go 之 captcha 生成图像验证码
目前 chptcha 好像只可以生成纯数字的图像验证码,不过对于普通简单应用来说也足够了。captcha默认将store封装到内部,未提供对外操作的接口,因此使用自己显式生成的store,可以通过store自定义要生成的验证码。 package mainimpor…...
【Java从入门到大牛】多线程
🔥 本文由 程序喵正在路上 原创,CSDN首发! 💖 系列专栏:Java从入门到大牛 🌠 首发时间:2023年11月18日 🦋 欢迎关注🖱点赞👍收藏🌟留言Ǵ…...
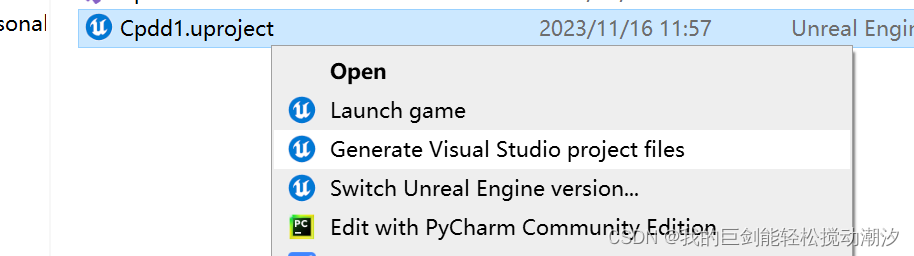
UE5 C++报错:is not currently enabled for Live Coding
解决办法: 再次打开项目,以此法打开:...
mysql服务器数据同步
在Linux和Windows之间实现MySQL服务器数据的同步。下面是一些常见的方法和工具: 复制(Replication):MySQL复制是一种常见的数据同步技术,可用于将一个MySQL服务器的数据复制到其他服务器。您可以设置主服务器ÿ…...

Docker Golang 开发环境搭建指南
Docker Golang 开发环境搭建指南 概述 在 Golang 开发中,搭建合适的开发环境是非常重要的。然而,由于 Golang 的跨平台特性,不同操作系统之间的配置差异可能会导致环境搭建过程变得复杂。为了简化这个过程并保持开发环境的一致性࿰…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...
