buu [BJDCTF2020]easyrsa 1
题目描述 :
from Crypto.Util.number import getPrime,bytes_to_long
from sympy import Derivative
from fractions import Fraction
from secret import flagp=getPrime(1024)
q=getPrime(1024)
e=65537
n=p*q
z=Fraction(1,Derivative(arctan(p),p))-Fraction(1,Derivative(arth(q),q))
m=bytes_to_long(flag)
c=pow(m,e,n)
print(c,z,n)
'''
output:
c = 7922547866857761459807491502654216283012776177789511549350672958101810281348402284098310147796549430689253803510994877420135537268549410652654479620858691324110367182025648788407041599943091386227543182157746202947099572389676084392706406084307657000104665696654409155006313203957292885743791715198781974205578654792123191584957665293208390453748369182333152809882312453359706147808198922916762773721726681588977103877454119043744889164529383188077499194932909643918696646876907327364751380953182517883134591810800848971719184808713694342985458103006676013451912221080252735948993692674899399826084848622145815461035
z = 32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482
n = 15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441
'''
题目分析:
- 首先这里遇到了两个没见过的函数 ----> Fraction() 和 Derivative()
Fraction(a,b) 相当于 a / b (a 除 b)
Derivative(a,b),前一个参数表示求导的内容,后一个参数表示求导的主体
Derivative(arctan § ,p)的意思是以p为主体对 arctan§ 求导,得到1/(1 + p^2),同理Derivative(arth(q),q) 得到 1/(1 - q^2)
最后
Fraction(1,Derivative(arctan§,p)) = 1 + p^2,Fraction(1,Derivative(arth(q),q) = 1 - q^2
- 得到关系式: z = p^2 +q^2,又 n = p * q,进一步得到关系式 :
(p + q) ^ 2 = z + 2n
(p - q) ^ 2 = z - 2n
用代码解出p,q
import gmpy2
from Crypto.Util.number import *e = 65537
n = 15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441
c = 7922547866857761459807491502654216283012776177789511549350672958101810281348402284098310147796549430689253803510994877420135537268549410652654479620858691324110367182025648788407041599943091386227543182157746202947099572389676084392706406084307657000104665696654409155006313203957292885743791715198781974205578654792123191584957665293208390453748369182333152809882312453359706147808198922916762773721726681588977103877454119043744889164529383188077499194932909643918696646876907327364751380953182517883134591810800848971719184808713694342985458103006676013451912221080252735948993692674899399826084848622145815461035
z = 32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482p = (gmpy2.iroot(z-2*n,2)[0] + gmpy2.iroot(z+2*n,2)[0]) // 2
q = n // p
phi_n = (p-1)*(q-1)
d = gmpy2.invert(e,phi_n)
m = gmpy2.powmod(c,d,n)
print(long_to_bytes(m))
- 得到flag{Advanced_mathematics_is_too_hard!!!}
此题还可以直接用在线网站分解n ,得到p,q,特别简单且快速,比较暴力。但,我喜欢!
收获与体会:
- 又了解了两个新函数:
Fraction(a,b) 相当于 a / b (a 除 b)
Derivative(a,b),前一个参数表示求导的内容,后一个参数表示求导的主体
- 对于有n的,多尝试能否暴力分解得p,q
相关文章:

buu [BJDCTF2020]easyrsa 1
题目描述 : from Crypto.Util.number import getPrime,bytes_to_long from sympy import Derivative from fractions import Fraction from secret import flagpgetPrime(1024) qgetPrime(1024) e65537 np*q zFraction(1,Derivative(arctan(p),p))-Fraction(1,Deri…...

taobao.user.openuid.getbyorder( 根据订单获取买家openuid )
¥免费不需用户授权 根据订单获取买家openuid,最大查询30个 公共参数 请求地址: HTTP地址 http://gw.api.taobao.com/router/rest 公共请求参数: 请求示例 TaobaoClient client new DefaultTaobaoClient(url, appkey, secret); UserOpenuidGetbyorderR…...
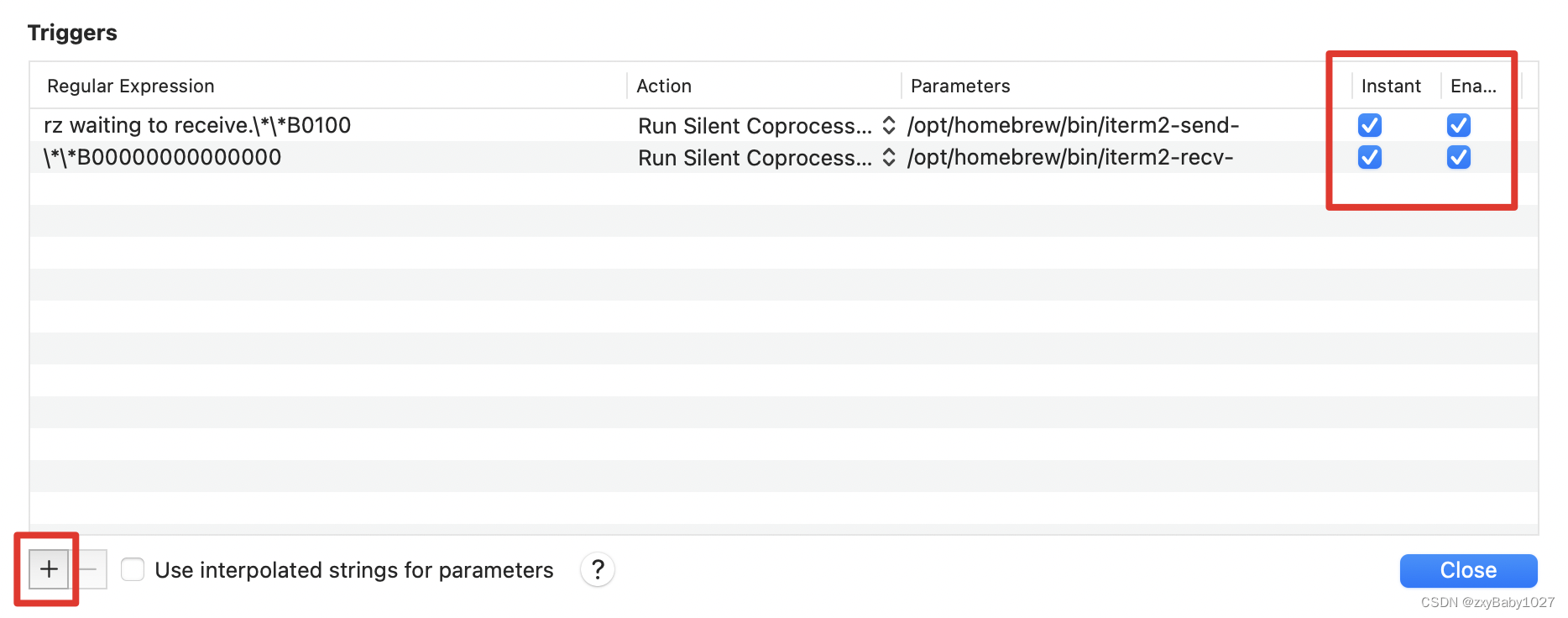
Mac iTerm2 rz sz
1、安装brew(找了很多🔗,就这个博主的好用) Mac如何安装brew?_行走的码农00的博客-CSDN博客_mac brew 2、安装lrzsz brew install lrzsz 检查是否安装成功 brew list 定位lrzsz的安装目录 brew list lrzsz 执…...
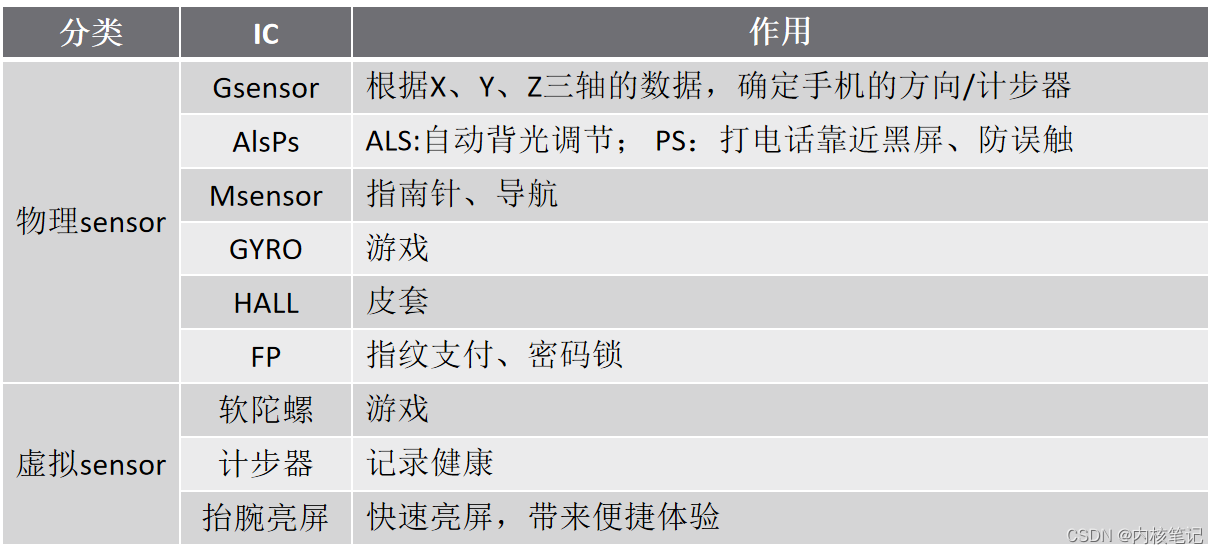
高通平台开发系列讲解(Sensor篇)Gsensor基础知识
文章目录 一、什么是SENSOR?二、Sensor的分类及作用三、Gsensor的工作原理及介绍3.1、常见Gsensor3.2、Gsensor的特性沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇文章将介绍 Sensor 基础 一、什么是SENSOR? 传感器(英文名称:sensor )是一种检测装置,能感…...

图像处理实战--Opencv实现人像迁移
前言: Hello大家好,我是Dream。 今天来学习一下如何使用Opencv实现人像迁移,欢迎大家一起参与探讨交流~ 本文目录:一、实验要求二、实验环境三、实验原理及操作1.照片准备2.图像增强3.实现美颜功能4.背景虚化5.图像二值化处理6.人…...
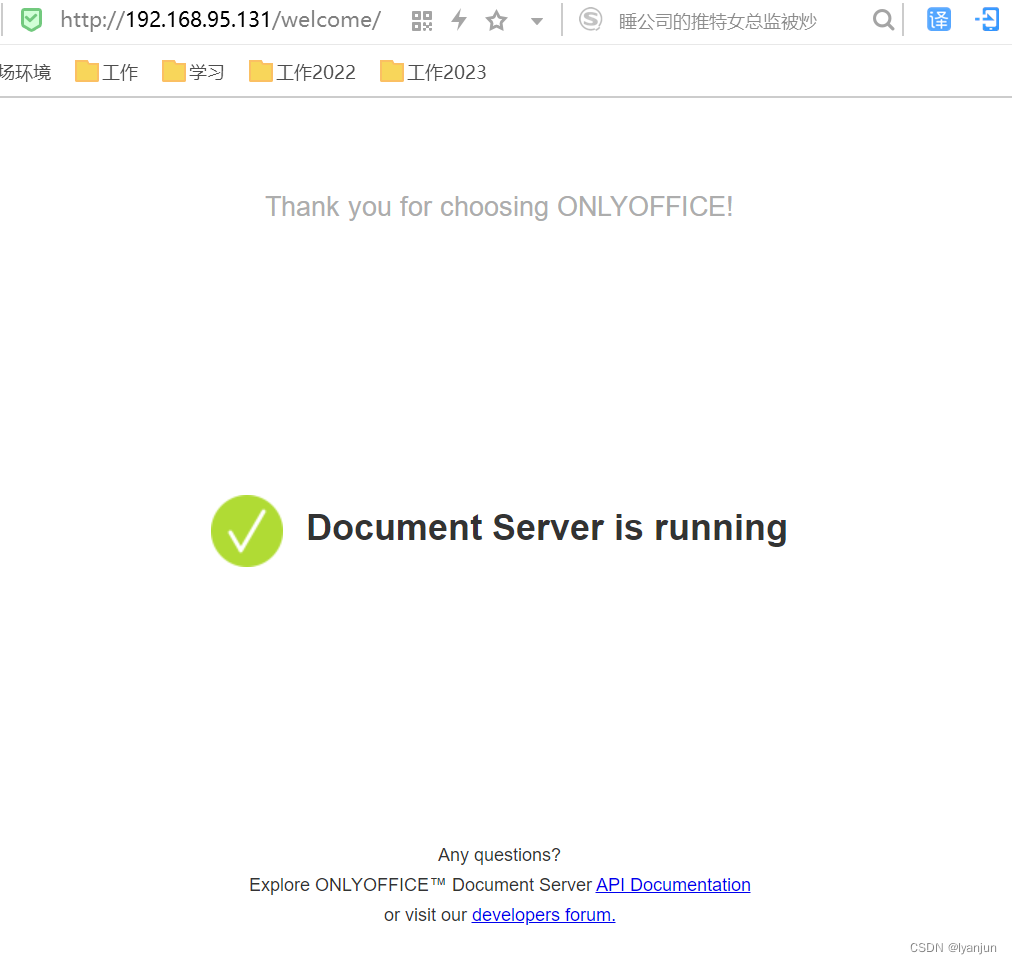
OnlyOffice验证(二)在Centos7上部署OnlyOffice编译结果
在Centos7上部署OnlyOffice编译结果 此处将尝试将OnlyOffice验证(一)DocumentServer编译验证的结果部署到Centos7上。并且使用其它服务器现有的RabbitMq和Mysql。 安装Nginx 先安装Nginx需要的依赖环境: yum install openssl* -y yum insta…...

6.补充和总结【Java面试第三季】
6.补充和总结【Java面试第三季】前言推荐6.补充和总结69_总结闲聊回顾和总结继续学习最后前言 2023-2-4 19:08:01 以下内容源自 【尚硅谷Java大厂面试题第3季,跳槽必刷题目必扫技术盲点(周阳主讲)-哔哩哔哩】 仅供学习交流使用 推荐 Jav…...

基于ssm框架大学生社团管理系统(源码+数据库+文档)
一、项目简介 本项目是一套基于ssm框架大学生社团管理系统,主要针对计算机相关专业的正在做bishe的学生和需要项目实战练习的Java学习者。 包含:项目源码、数据库脚本等,该项目可以直接作为bishe使用。 项目都经过严格调试,确保可…...
vulnhub靶场NAPPING: 1.0.1教程
靶场搭建靶机下载地址:Napping: 1.0.1 ~ VulnHub直接解压双击ova文件即可使用软件:靶机VirtualBox,攻击机VMware攻击机:kali信息收集arp-scan -l上帝之眼直接来看看网站可以注册账号,那就先试试。注册完后登入哦。要输…...

Docker基本介绍
最近需要将项目做成一个web应用并部署到多台服务器上,于是就简单学习了一下docker,做一下小小的记录。 1、简单介绍一下docker 我们经常遇到这样一个问题,自己写的代码在自己的电脑上运行的很流畅,在其他人电脑上就各种bug&…...
可用于标记蛋白质216699-36-4,6-ROX,SE,6-羧基-X-罗丹明琥珀酰亚胺酯
一.6-ROX,SE产品描述:6-羧基-X-罗丹明琥珀酰亚胺酯(6-ROX,SE)是一种用于寡核苷酸标记和自动DNA测序的荧光染料,可用于标记蛋白质,寡核苷酸和其他含胺分子的伯胺(-NH2)。西…...

高数:极限的定义
目录 极限的定义: 数列极限的几何意义: 由极限的定义得出的极限的两个结论: 编辑 极限的第三个结论: 例题 方法1: 编辑 方法2: 编辑 方法3: 编辑 极限的定义: 如何理…...
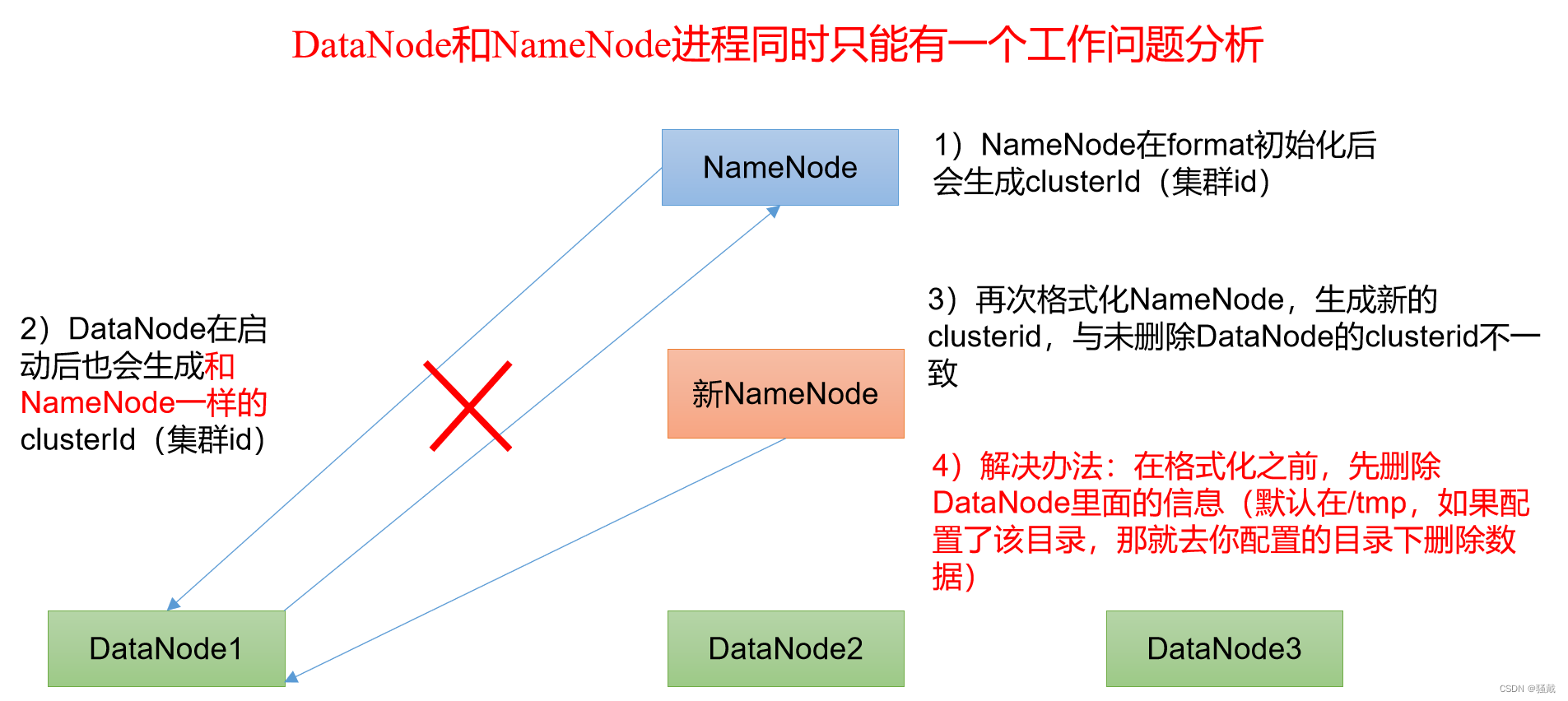
大数据技术之Hadoop
第1章 Hadoop概述1.1 Hadoop是什么1.2 Hadoop发展历史(了解)1.3 Hadoop三大发行版本(了解)Hadoop三大发行版本:Apache、Cloudera、Hortonworks。Apache版本最原始(最基础)的版本,对于…...

一文带你搞懂Go语言函数选项模式,Go函数一等公民。
前言 通过这篇文章《为什么说Go的函数是”一等公民“》,我们了解到了什么是“一等公民”,以及都具备哪些特性,同时对函数的基本使用也更加深入。 本文重点介绍下Go设计模式之函数选项模式,它得益于Go的函数是“一等公民”&#…...
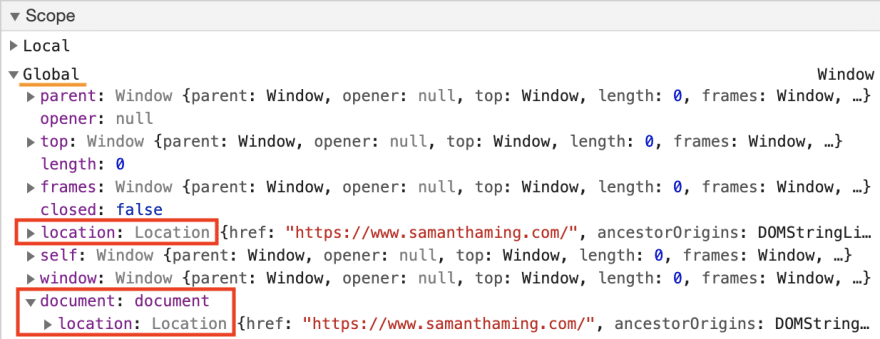
Window.location 详细介绍
如果你需要获取网站的 URL 信息,那么 window.location 对象就是为你准备的。使用它提供的属性来获取当前页面地址的信息,或使用其方法进行某些页面的重定向或刷新。 https://www.samanthaming.com/tidbits/?filterJS#2 window.location.origin → htt…...

js侧滑显示删除按钮
效果图: <!DOCTYPE html> <html><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0, maximum-scale1.0, user-scalableno"><title>js侧滑显示删…...

Python - DIY - 使用dump取json某些键值对合成新的json文件
Python - Json处理前言:应用场景:基本工具:文件操作:打开文件:写文件:读文件:关闭文件并刷新缓冲区:Json字符串和字典转换:json.loads():json.dumps():Json文…...

深度剖析指针(中)——“C”
各位CSDN的uu们你们好呀,今天小雅兰的内容仍旧是深度剖析指针噢,在上一篇博客中,我已经写过了字符指针、数组指针、指针数组、数组传参和指针传参的知识点,那么这篇博客小雅兰会讲解一下函数指针、函数指针数组 、指向函数指针数组…...
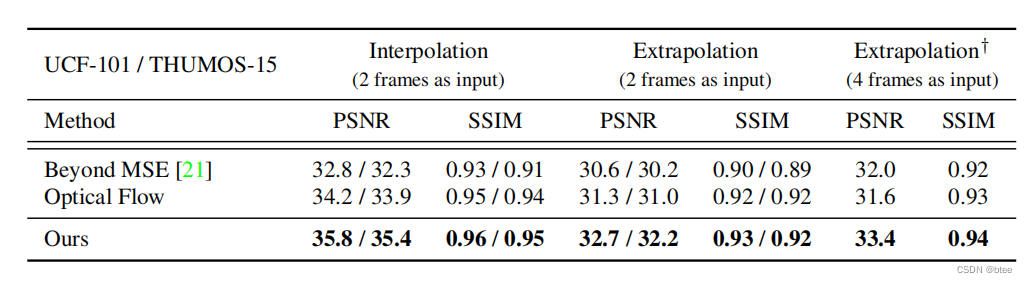
论文阅读 | Video Frame Synthesis using Deep Voxel Flow
前言: 视频帧生成方法(视频插帧/视频预测)ICCV2017 oral Video Frame Synthesis using Deep Voxel Flow 引言 当下进行视频帧合成的方法分为两种,第一种是光流法,光流准确的话效果好,光流不准确的话则生…...

我所理解的生活
诞生 人真正意义上的诞生应该是社会学意义上的,是一种意识到自我、自我与社会关系的存在,只有这种诞生,才是完整人生的基点,大千世界中,唯有人类以生活作为自己的存在方式,除人类以外,从无机界…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...
