高数:极限的定义
目录
极限的定义:
数列极限的几何意义:
由极限的定义得出的极限的两个结论:
编辑
极限的第三个结论:
例题
方法1: 编辑
方法2: 编辑
方法3:
编辑
极限的定义:

如何理解呢?
极限的通俗理解:
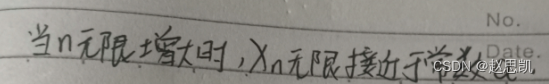
用数列的语言来说:
当数列的项数n无限增大时,数列的项要多接近就有多接近与a。
![]()
我们如何理解?
答:首先,我们要清楚,极限是一个无限的过程,对于无限的过程,我们要以有限的形式进行表达,上图就是我们对于极限的有限表达。
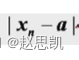
|Xn-a|是什么意思?
答:首先要清楚Xn的意思是数列的第n项,a表示我们的极限值,所以 |Xn-a|表示我们数列的项和极限值的接近程度。

这是什么意思?
答:

为什么要使用'任意'符号?
答:

这里是什么意思?
答:存在N,让N以后的项无限接近于常数a,这个N其实是不存在的,因为极限是一个无限的过程,我们假设N存在,N之后的元素是无限接近于常数a的,所以N只是用来刻画n无限增大以至于无限接近于常数a的这个过程。
数列极限的几何意义:

等价于:
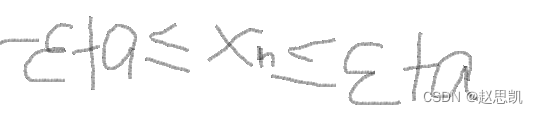
这时候就形成一个领域:
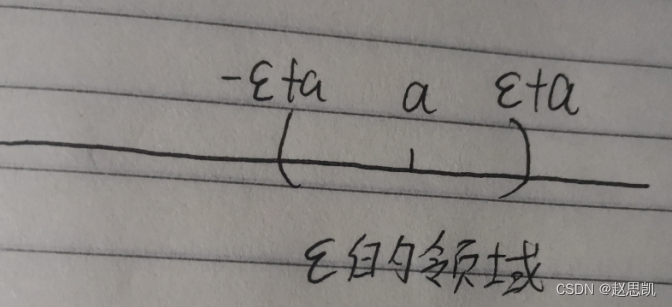
我们可以把N当作数列有限项与无限项的分割线:

在N之后的数列中的项是放在领域之内的:

在领域中的无限项表示无限接近于极限值a。

一句话总结数列极限的定义:
由极限的定义得出的极限的两个结论:
我们对结论1进行阐述:
答:a表示我们数列的极限,当b<a时,也就是b小于数列的极限,存在N,这个N之后的无限项全部无限接近于a值,所以当n大于N时,对应的项全部无限接近于a值,而b<a,则N之后所有的项都大于b。
我们对结论2进行阐述:
答:a表示数列的极限,当c>a时,也就是c大于数列的极限,所以N之后的无限项全部无限接近于a值,但是比a值小,因为c值比a值大,所以N之后的无限项全部小于c值。
极限的第三个结论:
数列Xn的极限与数列的前n项无关。
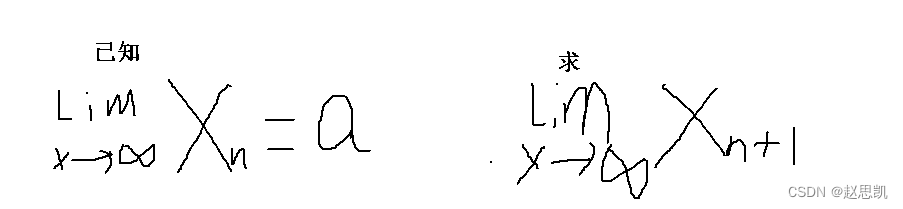
Xn+1相当于去掉了数列的第一项,数列的第一项并不影响我们的极限值。
所以:

我们之前知道一个结论:单调有界一定有极限。
单调有界不一定要从第一项就开始单调,在某一段区间上单调他也有极限。
例题1:

结果依然为1,因为右式是数列Xn的奇数部分,也是原来数列的部分项,所以又叫右式为数列Xn的奇数列。
奇数列和偶数列都是原来数列的部分项,所以奇数列和偶数列的极限也等于原数列的极限值a。
所以数列有极限可以推导出数列的奇数列和偶数列都有极限,但是数列的奇数列或者偶数列都有极限可以推导出数列有极限吗?
答:并不能,例如:

数列的奇数列为:
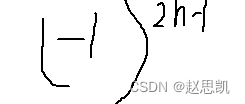
奇数列全为-1,所以奇数列的极限值也为-1.
数列的偶数列为:

偶数列全为1,所以偶数列的极限值也为1.
虽然奇数列和偶数列都有极限值,但是他们的极限值不同,所以无法推导出数列有极限。
当奇数列和偶数列都有极限值,并且奇数列和偶数列的极限值相同的情况下==>数列有极限。
答:因为奇数列和偶数列虽然是数列的部分列,但是这两个部分列的集合包括了数列的所有项,所有的项的极限值都以a为极限,则该数列的极限值为a。
例题

方法1: 
方法2: 
方法3:
相关文章:

高数:极限的定义
目录 极限的定义: 数列极限的几何意义: 由极限的定义得出的极限的两个结论: 编辑 极限的第三个结论: 例题 方法1: 编辑 方法2: 编辑 方法3: 编辑 极限的定义: 如何理…...
大数据技术之Hadoop
第1章 Hadoop概述1.1 Hadoop是什么1.2 Hadoop发展历史(了解)1.3 Hadoop三大发行版本(了解)Hadoop三大发行版本:Apache、Cloudera、Hortonworks。Apache版本最原始(最基础)的版本,对于…...

一文带你搞懂Go语言函数选项模式,Go函数一等公民。
前言 通过这篇文章《为什么说Go的函数是”一等公民“》,我们了解到了什么是“一等公民”,以及都具备哪些特性,同时对函数的基本使用也更加深入。 本文重点介绍下Go设计模式之函数选项模式,它得益于Go的函数是“一等公民”&#…...
Window.location 详细介绍
如果你需要获取网站的 URL 信息,那么 window.location 对象就是为你准备的。使用它提供的属性来获取当前页面地址的信息,或使用其方法进行某些页面的重定向或刷新。 https://www.samanthaming.com/tidbits/?filterJS#2 window.location.origin → htt…...

js侧滑显示删除按钮
效果图: <!DOCTYPE html> <html><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0, maximum-scale1.0, user-scalableno"><title>js侧滑显示删…...

Python - DIY - 使用dump取json某些键值对合成新的json文件
Python - Json处理前言:应用场景:基本工具:文件操作:打开文件:写文件:读文件:关闭文件并刷新缓冲区:Json字符串和字典转换:json.loads():json.dumps():Json文…...

深度剖析指针(中)——“C”
各位CSDN的uu们你们好呀,今天小雅兰的内容仍旧是深度剖析指针噢,在上一篇博客中,我已经写过了字符指针、数组指针、指针数组、数组传参和指针传参的知识点,那么这篇博客小雅兰会讲解一下函数指针、函数指针数组 、指向函数指针数组…...
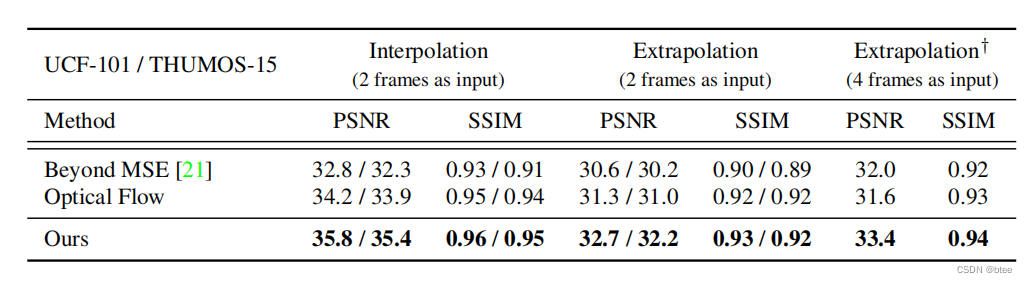
论文阅读 | Video Frame Synthesis using Deep Voxel Flow
前言: 视频帧生成方法(视频插帧/视频预测)ICCV2017 oral Video Frame Synthesis using Deep Voxel Flow 引言 当下进行视频帧合成的方法分为两种,第一种是光流法,光流准确的话效果好,光流不准确的话则生…...

我所理解的生活
诞生 人真正意义上的诞生应该是社会学意义上的,是一种意识到自我、自我与社会关系的存在,只有这种诞生,才是完整人生的基点,大千世界中,唯有人类以生活作为自己的存在方式,除人类以外,从无机界…...

debian 部署nginx https
我是flask 处理请求单进程, 差点意思 , 考虑先flask 在往下走 一:安装nginx 因为我是debian 系统,所以我的建议是直接 sudo apt-get install nginx 你也可以选择在官网下载, 但是我搭建ssl 的时候安装openssl非常的麻…...
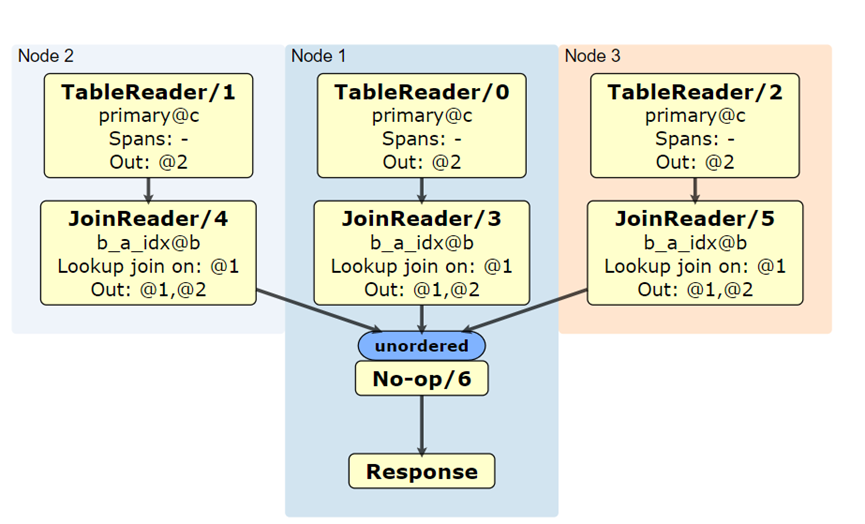
SQL 层功能改进 - lookupJoin 的优化
一、传统 join 算法lookupJoin 是 join 查询的一种,传统 join 算法为:1. 遍历 A 表,读取一条数据 r2. 遍历 B 表,对于每条数据,与 r 进行 join 操作3. 重复 1、2 操作,直到 A 表遍历完所有数据二、lookupJo…...

动态规划:鸣人的影分身
在火影忍者的世界里,令敌人捉摸不透是非常关键的。我们的主角漩涡鸣人所拥有的一个招数——多重影分身之术——就是一个很好的例子。影分身是由鸣人身体的查克拉能量制造的,使用的查克拉越多,制造出的影分身越强。针对不同的作战情况…...
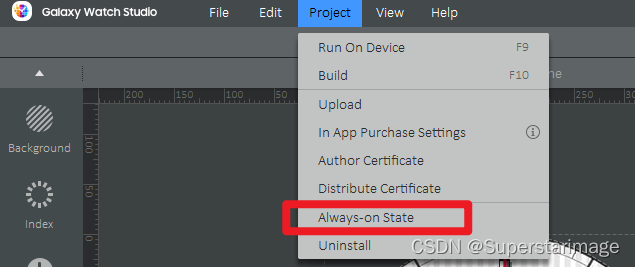
如何为三星active2手表安装自己DIY的表盘
一、步骤介绍 Step 1. 下载Galaxy watch studio; Step 2. 按照up主“隔壁张师傅2022”的文章进行安装。 二、安装流程简单说明: ① 电脑端官网下载并安装Galaxy Watch Designer或者Galaxy Watch Studio程序。 ② 关闭手表蓝牙连接,并打开调…...

Android 项目必备(四十二)-->Android 多窗口模式
简介 自由窗口模式: 该模式类似于常见的桌面操作系统, 应用界面的窗口可以自由的拖动和修改大小。 分屏模式 该模式可以在手机上使用, 该模式将屏幕一分为二, 同时显示两个应用界面。 画中画模式: 该模式主要用于TV, 在该模式下…...
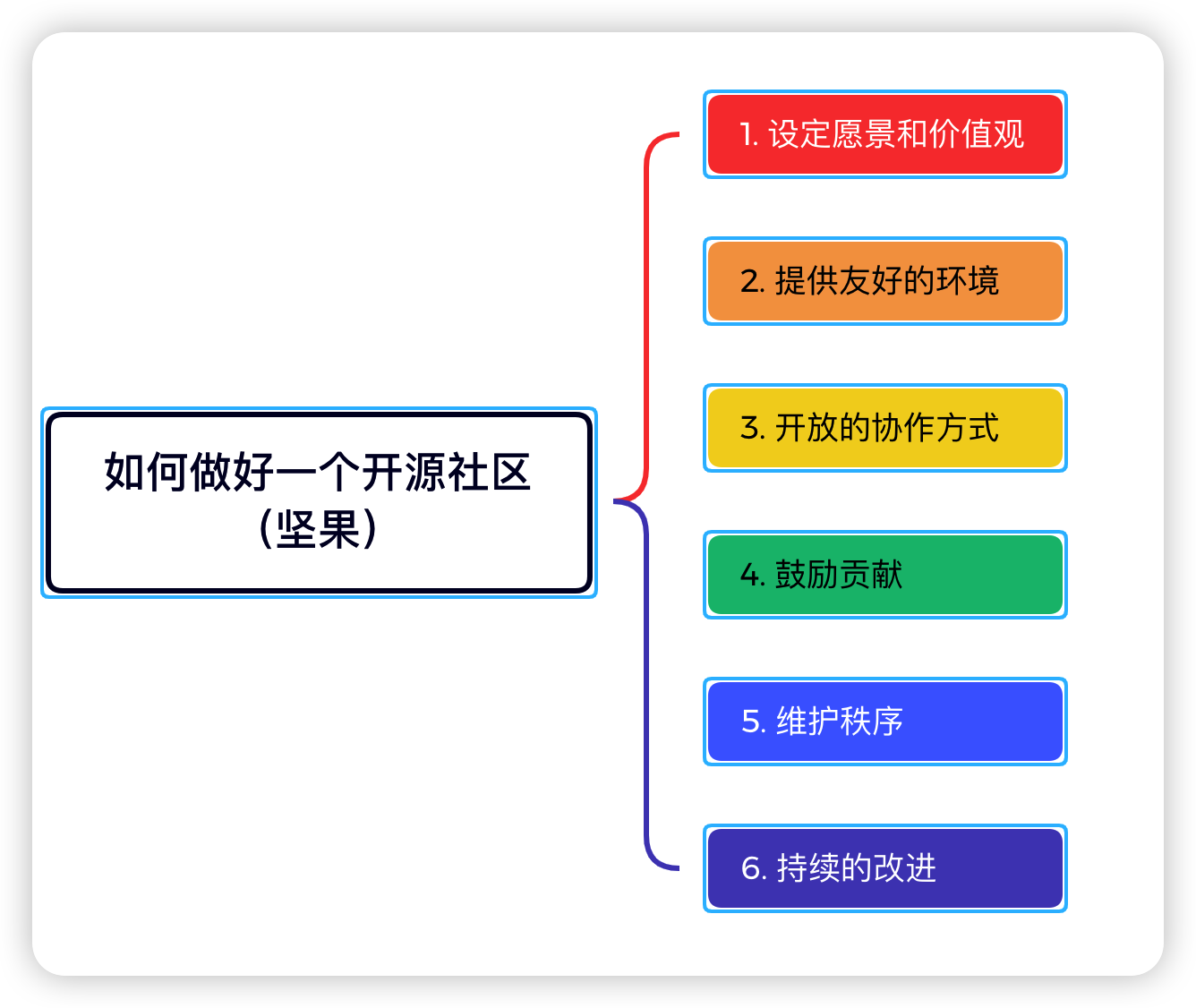
OpenHarmony的未来和如何做好一个开源社区
今天要分享的文章,可能更多只是作为一种观点。主要包括2个内容。OpenHarmony的未来和如何做好一个开源社区,好的,接下来开始今天的内容。 你对OpenHarmony的未来如何看待? OpenHarmony的未来看起来非常光明,因为它具…...
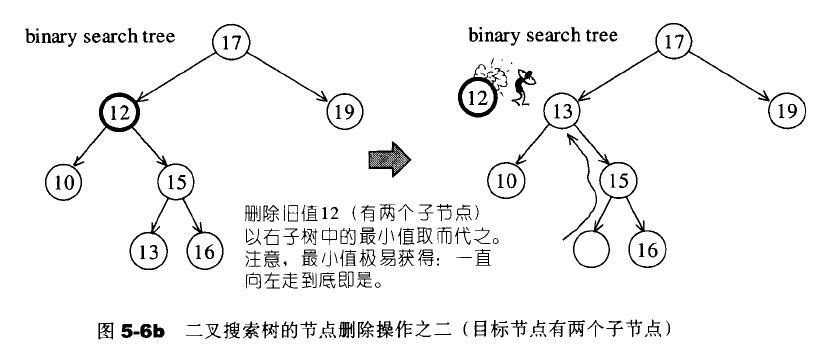
二叉搜索树实现
树的导览 树由节点(nodes)和边(edges)构成,如下图所示。整棵树有一个最上端节点,称为根节点(root)。每个节点可以拥有具有方向的边(directed edges)…...
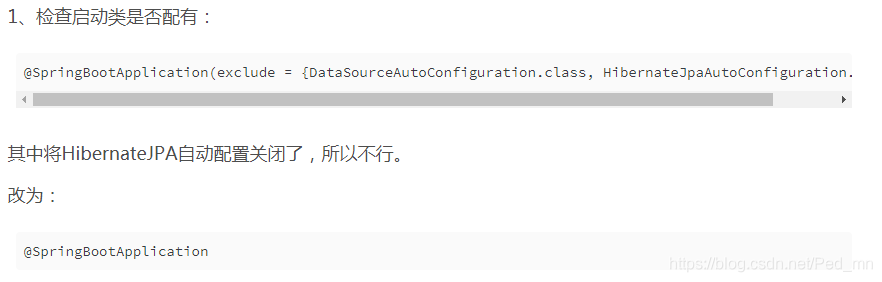
解决Spring Data Jpa 实体类自动创建数据库表失败问题
先说一下我遇到的这个问题,首先我是通过maven创建了一个spring boot的工程,引入了Spring data jpa,结果实体类创建好之后,运行工程却没有在数据库中自动创建数据表。 找了半天发现是一个配置的问题! hibernate.ddl-auto节点的配…...

Elasticsearch:创建一个简单的 “你的意思是?” 推荐搜索
“你的意思是” 是搜索引擎中一个非常重要的功能,因为它们通过显示建议的术语来帮助用户,以便他可以进行更准确的搜索。比如,在百度中,我们进行搜索时,它通常会显示一些更为常用推荐的搜索选项来供我们选择:…...
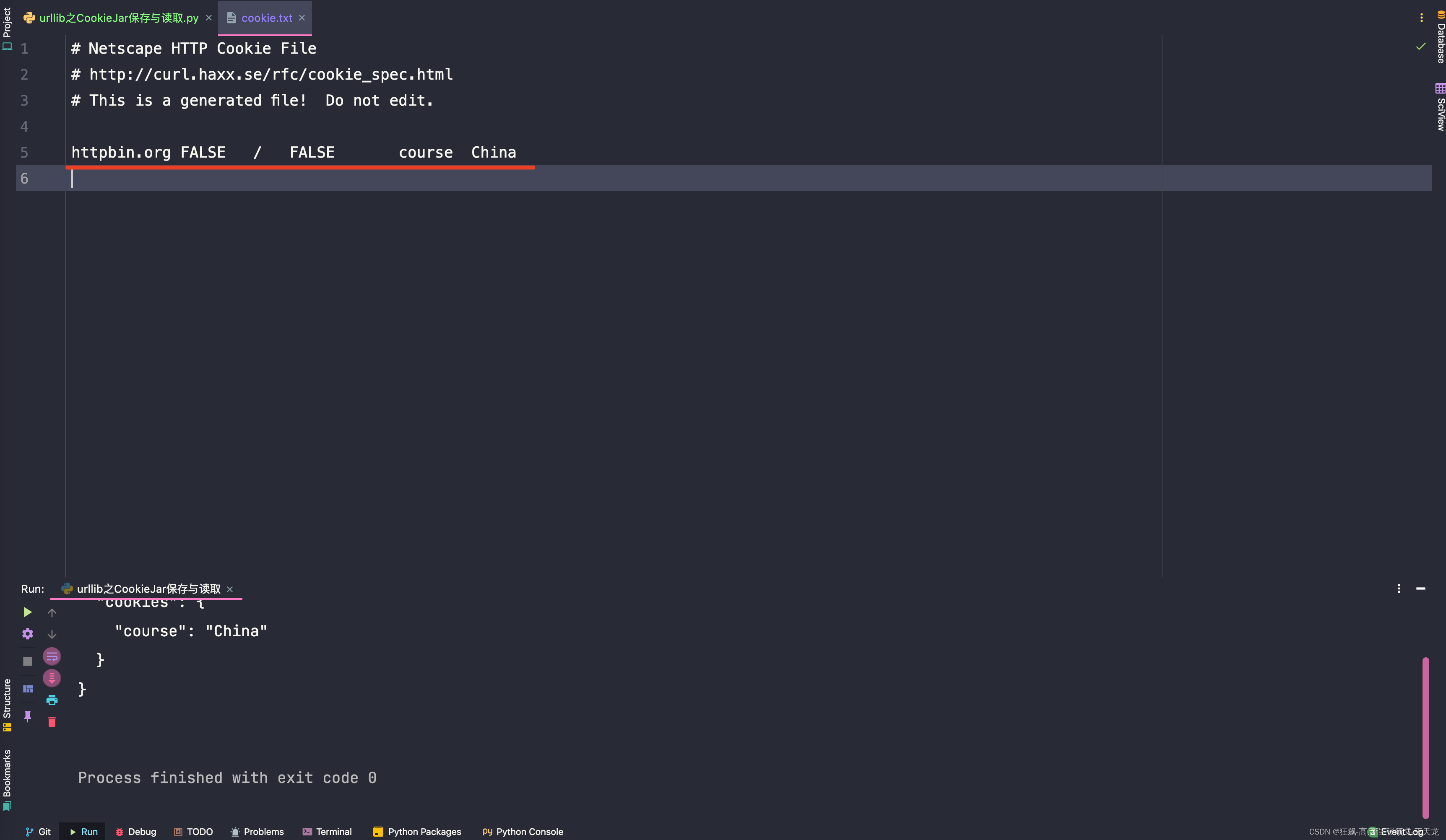
urllib之ProxyHandler代理以及CookieJar的cookie内存传递和本地保存与读取的使用详解
处理更高级操作时(Cookies处理,代理设置),需要一个强大的工具Handler,可以理解成各种处理器,有处理登录认证的、有处理Cookies的、有处理代理设置的。利用这些几乎可以做到HTTP请求中所有事情。当中urllib.request模块里的 BaseHa…...

华为造车锚定智选模式, 起点赢家赛力斯驶入新能源主航道
文|螳螂观察 作者| 易不二 近日,赛力斯与华为的一纸联合业务深化合作协议,给了频频猜测赛力斯与华为之间关系的舆论一个明确的定调:智选模式已成为华为与赛力斯共同推动中国新能源汽车产业高质量发展的坚定选择。 自华为智能汽车业务开启零…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...


