蓝桥杯-最长公共子序列(线性dp)
没有白走的路,每一步都算数🎈🎈🎈
题目描述:
已知有两个数组a,b。已知每个数组的长度。要求求出两个数组的最长公共子序列
序列 1 2 3 4 5 序列 2 3 2 1 4 5
子序列:从其中抽掉某个或多个元素而产生的新序列。其中子序列可以和本身一样
这里1 2 3 4 5的子序列挺多,总共有这么多个
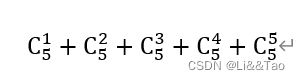
同理 2 3 2 1 4 5的子序列也有很多,但是应该比下面的要少,因为出现重复的元素
![]()
公共子序列:即两个序列中共有的部分
长度为1的:1 2 3 4 5
部分长度为2的: 23
部分长度为3的: 234
长度为4的:2345
最长公共子序列:最长的公共子序列
2 3 4 5
输入描述:
第一行:
输入N,M表示两个数组的长度
第二行:
数组a中的元素
第三行:
数组b中的元素
输出描述:
输出两个数组的最长公共子序列的长度
样例输入输出:
样例输入:
5 6
1 2 3 4 5
2 3 2 1 4 5
样例输出:
4
算法分析:
import os
import sys
n,m = map(int,input().split())
a = [0]+[int(i) for i in input().split()]
b = [0]+[int(i) for i in input().split()]
dp = [[0]*(m+1) for i in range(n+1)]
for i in range(1,n+1):for j in range(1,m+1):if a[i] == b[j]:dp[i][j] = dp[i-1][j-1]+1else:dp[i][j] = max(dp[i-1][j],dp[i][j-1])
print(dp[n][m])每日一句
摘自《三体》:
生存在宇宙中,本身就是一件很幸运的事情,但是不知道什么时候起,你们有了这样一种幻想,认为生存是唾手可得的,这就是你们失败因的根本原。
相关文章:
蓝桥杯-最长公共子序列(线性dp)
没有白走的路,每一步都算数🎈🎈🎈 题目描述: 已知有两个数组a,b。已知每个数组的长度。要求求出两个数组的最长公共子序列 序列 1 2 3 4 5 序列 2 3 2 1 4 5 子序列:从其中抽掉某个或多个元素而产生的新…...

GO的并发模式Context
GO的并发模式Context 文章目录GO的并发模式Context一、介绍二、Context三、context的衍生四、示例:Google Web Search4.1 server程序4.2 userip 包4.3 google 包五、使用context包中程序实体实现sync.WaitGroup同样的功能(1)使用sync.WaitGro…...
《Redis实战篇》六、秒杀优化
6、秒杀优化 6.0 压力测试 目的:测试1000个用户抢购优惠券时秒杀功能的并发性能~ ①数据库中创建1000用户 这里推荐使用开源工具:https://www.sqlfather.com/ ,导入以下配置即可一键生成模拟数据 {"dbName":"hmdp",…...
)
《C++ Primer Plus》第16章:string类和标准模板库(11)
其他库 C 还提供了其他一些类库,它们比本章讨论前面的例子更为专用。例如,头文件 complex 为复数提供了类模板 complex,包含用于 float、long 和 long double 的具体化。这个类提供了标准的复数运算及能够处理复数的标准函数。C11 新增的头文…...

声明和定义
前言 很多编程语言的语法中都有关于声明和定义的概念,这种概念一般会应用于函数或变量的创建和使用中,但是为什么要这么做? 以C语言为例,一些书籍或教程会要求读者在程序文件开头写上函数和变量的声明,然后再在后面对…...

Python获取最小路径,查找元素在list中的坐标
# codingutf-8__author__ Jeff.xiedef t(li):pass获取最小路径def minPathSum(grid):if not grid:return 0m len(grid) #m列n len(grid[0]) #n行print(grid[0])print("m: ",m)print("n: ",n)#创建一个二维数组dp [[0]*n for _ in range(m)]print(dp) #这…...

数据采集协同架构,集成马扎克、西门子、海德汉、广数、凯恩帝、三菱、海德汉、兄弟、哈斯、宝元、新代、发那科、华中各类数控以及各类PLC数据采集软件
文章目录 前言一、采集协同架构是什么?可以做什么(数控、PLC配置采集)?二、使用步骤 1.打开软件,配置MQTT或者数据库(支持sqlserver、mysql等)存储转发消息规则2.配置数控系统所采集的参数、转…...
Allegro172版本如何用自带的功能实现快速在1MMBGA下方等距放置电容
Allegro172版本如何用自带的功能实现快速在1MMBGA下方等距放置电容 在做PCB设计的时候,在1MM中心间距的BGA背面放置电容,是非常常见的设计,如何快速把电容等距放在BGA下方,除了借助辅助工具外,在Allegro升级到了172版本的时候,可以借助本身自带的功能实现快速放置,以下图…...

一种简单的统计pytorch模型参数量的方法
nelememt()函数Tensor.nelement()->引自Tensor.numel()->引自torch.numel(input)三者的作用是相同的Returns the total number of elements in the inputtensor.返回当前tensor的元素数量利用上面的函数刚好可以统计模型的参数数量parameters()函数Module.parameters(rec…...

【PyTorch】教程:对抗学习实例生成
ADVERSARIAL EXAMPLE GENERATION 研究推动 ML 模型变得更快、更准、更高效。设计和模型的安全性和鲁棒性经常被忽视,尤其是面对那些想愚弄模型故意对抗时。 本教程将提供您对 ML 模型的安全漏洞的认识,并将深入了解对抗性机器学习这一热门话题。在图像…...

中国区使用Open AI账号试用Chat GPT指南
最近推出强大的ChatGPT功能,各大程序员使用后发出感叹:程序员要失业了 不过在国内并不支持OpenAI账号注册,多数会提示: OpenAI’s services are not available in your country. 经过一番搜索后,发现如下方案可以完…...
STM32开发(9)----CubeMX配置外部中断
CubeMX配置外部中断前言一、什么是中断1.STM32中断架构体系2.外部中断/事件控制器(EXTI)3.嵌套向量中断控制器(NIVC)二、实验过程1.CubeMX配置2.代码实现3.硬件连接4.实验结果总结前言 本章介绍使用STM32CubeMX对引脚的外部中断进…...
Nextjs了解内容
目录Next.jsnext.js的实现1,nextjs初始化2, 项目结构3, 数据注入getInitialPropsgetServerSidePropsgetStaticProps客户端注入3,CSS Modules4,layout组件5,文件式路由6,BFF层的文件式路由7&…...

从事功能测试1年,裸辞1个月,找不到工作的“我”怎么办?
做功能测试一年多了裸辞职一个月了,大部分公司都要求有自动化测试经验,可是哪来的自动化测试呢? 我要是简历上写了吧又有欺诈性,不写他们给的招聘又要自动化优先,将项目带向自动化不是一个容易的事情,很多…...

机器学习基本原理总结
本文大部分内容参考《深度学习》书籍,从中抽取重要的知识点,并对部分概念和原理加以自己的总结,适合当作原书的补充资料阅读,也可当作快速阅览机器学习原理基础知识的参考资料。 前言 深度学习是机器学习的一个特定分支。我们要想…...
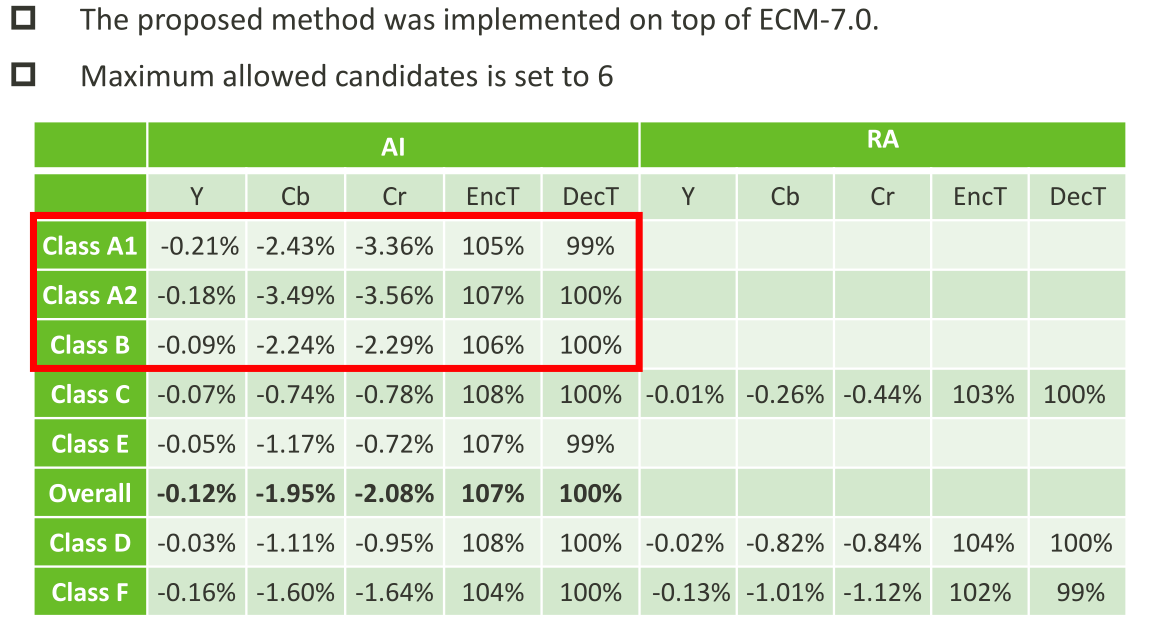
JVET-AC0315:用于色度帧内预测的跨分量Merge模式
ECM采用了许多跨分量的预测(Cross-componentprediction,CCP)模式,包括跨分量包括跨分量线性模型(CCLM)、卷积跨分量模型(CCCM)和梯度线性模型(GLM)࿰…...
)
Session与Cookie的区别(二)
脸盲症的困扰 小明身为杂货店的店长兼唯一的店员,所有大小事都是他一个人在处理。传统杂货店跟便利商店最大的差别在哪里?在于人情味。 就像是你去菜市场买菜的时候会被说帅哥或美女,或者是去买早餐的时候老板会问你:「一样&#…...
疫情开发,软件测试行情趋势是怎么样的?
如果说,2022年对于全世界来说,都是一场极大的挑战的话;那么,2023年绝对是机遇多多的一年。众所周知,随着疫情在全球范围内逐步得到控制,无论是国际还是国内的环境,都会呈现逐步回升的趋势&#…...

Java中间件描述与使用,面试可以用
myCat 用于切分mysql数据库(为什么要切分:当数据量过大时,mysql查询效率变低) ActiveMQ 订阅,消息推送 swagger 前后端分离,后台接口调式 dubbo 阿里的面向服务RPC框架,为什么要面向服务&#x…...

[OpenMMLab]AI实战营第七节课
语义分割代码实战教学 HRNet 高分辨率神经网络 安装配置 # 选择分支 git branch -a git switch 3.x # 配置环境 conda create -n mmsegmentation python3.8 conda activate mmsegmentation pip install torch1.11.0cu113 torchvision0.12.0cu113 torchaudio0.11.0 --extra-i…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

2025 后端自学UNIAPP【项目实战:旅游项目】7、景点详情页面【完结】
1、获取景点详情的请求【my_api.js】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http(/login/getWXSessionKey, {code,avatar}); };//…...
