全网资料最全Java数据结构与算法-----算法分析
算法分析
研究算法的最终目的就是如何花更少的时间,如何占用更少的内存去完成相同的需求,并且也通过案例演示了不同算法之间时间耗费和空间耗费上的差异,但我们并不能将时间占用和空间占用量化,因此,接下来我们要学习有关算法时间耗费和算法空间耗费的描述和分析。有关算法时间耗费分析,我们称之为算法的时间复杂度分析,有关算法的空间耗费分析,我们称之为算法的空间复杂度分析。
算法的时间复杂度分析
我们要计算算法时间耗费情况,首先我们得度量算法的执行时间,那么如何度量呢?
事后分析估算方法:
比较容易想到的方法就是我们把算法执行若干次,然后拿个计时器在旁边计时,这种事后统计的方法看上去的确不错,并且也并非要我们真的拿个计算器在旁边计算,因为计算机都提供了计时的功能。这种统计方法主要是通过设计好的测试程序和测试数据,利用计算机计时器对不同的算法编制的程序的运行时间进行比较,从而确定算法效率的高低,但是这种方法有很大的缺陷:必须依据算法实现编制好的测试程序,通常要花费大量时间和精力,测试完了如果发现测试的是非常糟糕的算法,那么之前所做的事情就全部白费了,并且不同的测试环境(硬件环境)的差别导致测试的结果差异也很大。
public static void main(String[] args) {
long start = System.currentTimeMillis();
int sum = 0;
int n=100;
for (int i = 1; i <= n; i++) {
sum += i;
}
System.out.println("sum=" + sum);
long end = System.currentTimeMillis();
System.out.println(end-start);
}事前分析估算方法:
在计算机程序编写前,依据统计方法对算法进行估算,经过总结,我们发现一个高级语言编写的程序程序在计算机
上运行所消耗的时间取决于下列因素:
1.算法采用的策略和方案;
2.编译产生的代码质量;
3.问题的输入规模(所谓的问题输入规模就是输入量的多少);
4.机器执行指令的速度;
由此可见,抛开这些与计算机硬件、软件有关的因素,一个程序的运行时间依赖于算法的好坏和问题的输入规模。
如果算法固定,那么该算法的执行时间就只和问题的输入规模有关系了。
我么再次以之前的求和案例为例,进行分析。
需求:
计算1到100的和。
第一种解法:
如果输入量为n为1,则需要计算1次;
如果输入量n为1亿,则需要计算1亿次;
public static void main(String[] args) {
int sum = 0;//执行1次
int n=100;//执行1次
for (int i = 1; i <= n; i++) {//执行了n+1次
sum += i;//执行了n次
}
System.out.println("sum=" + sum);
}第二种解法:
如果输入量为n为1,则需要计算1次;
如果输入量n为1亿,则需要计算1次;
public static void main(String[] args) {
int sum = 0;//执行1次
int n=100;//执行1次
sum = (n+1)*n/2;//执行1次
System.out.println("sum="+sum);
}因此,当输入规模为n时,第一种算法执行了1+1+(n+1)+n=2n+3次;第二种算法执行了1+1+1=3次。如果我们把
第一种算法的循环体看做是一个整体,忽略结束条件的判断,那么其实这两个算法运行时间的差距就是n和1的差
距。
为什么循环判断在算法1里执行了n+1次,看起来是个不小的数量,但是却可以忽略呢?我们来看下一个例子:
需求:
计算100个1+100个2+100个3+...100个100的结果
代码:
public static void main(String[] args) {
int sum=0;
int n=100;
for (int i = 1; i <=n ; i++) {
for (int j = 1; j <=n ; j++) {
sum+=i;
}
}
System.out.println("sum="+sum);
}上面这个例子中,如果我们要精确的研究循环的条件执行了多少次,是一件很麻烦的事情,并且,由于真正计算和的代码是内循环的循环体,所以,在研究算法的效率时,我们只考虑核心代码的执行次数,这样可以简化分析。
我们研究算法复杂度,侧重的是当输入规模不断增大时,算法的增长量的一个抽象(规律),而不是精确地定位需要执行多少次,因为如果是这样的话,我们又得考虑回编译期优化等问题,容易主次跌倒。我们不关心编写程序所用的语言是什么,也不关心这些程序将跑在什么样的计算机上,我们只关心它所实现的算法。这样,不计那些循环索引的递增和循环终止的条件、变量声明、打印结果等操作,最终在分析程序的运行时间时,最重要的是把程序看做是独立于程序设计语言的算法或一系列步骤。我们分析一个算法的运行时间,最重要的就是把核心操作的次数和输入规模关联起来。

函数渐近增长
给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n>N,f(n)总是比g(n)大,那么我们说f(n)的增长渐近快于g(n)。
概念似乎有点艰涩难懂,那接下来我们做几个测试。
测试一:
假设四个算法的输入规模都是n:
1.算法A1要做2n+3次操作,可以这么理解:先执行n次循环,执行完毕后,再有一个n次循环,最后有3次运算;
2.算法A2要做2n次操作;
3.算法B1要做3n+1次操作,可以这个理解:先执行n次循环,再执行一个n次循环,再执行一个n次循环,最后有1
次运算。
4.算法B2要做3n次操作;
那么,上述算法,哪一个更快一些呢?

通过数据表格,比较算法A1和算法B1:
当输入规模n=1时,A1需要执行5次,B1需要执行4次,所以A1的效率比B1的效率低;
当输入规模n=2时,A1需要执行7次,B1需要执行7次,所以A1的效率和B1的效率一样;
当输入规模n>2时,A1需要的执行次数一直比B1需要执行的次数少,所以A1的效率比B1的效率高;
所以我们可以得出结论:
当输入规模n>2时,算法A1的渐近增长小于算法B1 的渐近增长
通过观察折线图,我们发现,随着输入规模的增大,算法A1和算法A2逐渐重叠到一块,算法B1和算法B2逐渐重叠
到一块,所以我们得出结论:
随着输入规模的增大,算法的常数操作可以忽略不计
测试二:
假设四个算法的输入规模都是n:
1.算法C1需要做4n+8次操作
2.算法C2需要做n次操作
3.算法D1需要做2n^2次操作
4.算法D2需要做n^2次操作
那么上述算法,哪个更快一些?
 通过数据表格,对比算法C1和算法D1:
通过数据表格,对比算法C1和算法D1:
当输入规模n<=3时,算法C1执行次数多于算法D1,因此算法C1效率低一些;
当输入规模n>3时,算法C1执行次数少于算法D1,因此,算法D2效率低一些,
所以,总体上,算法C1要优于算法D1.
通过折线图,对比对比算法C1和C2:
随着输入规模的增大,算法C1和算法C2几乎重叠
通过折线图,对比算法C系列和算法D系列:
随着输入规模的增大,即使去除n^2前面的常数因子,D系列的次数要远远高于C系列。
因此,可以得出结论:
随着输入规模的增大,与最高次项相乘的常数可以忽略
测试三:
假设四个算法的输入规模都是n:
算法E1:
2n^2+3n+1;
算法E2:
n^2
算法F1:
2n^3+3n+1
算法F2:
n^3
那么上述算法,哪个更快一些?

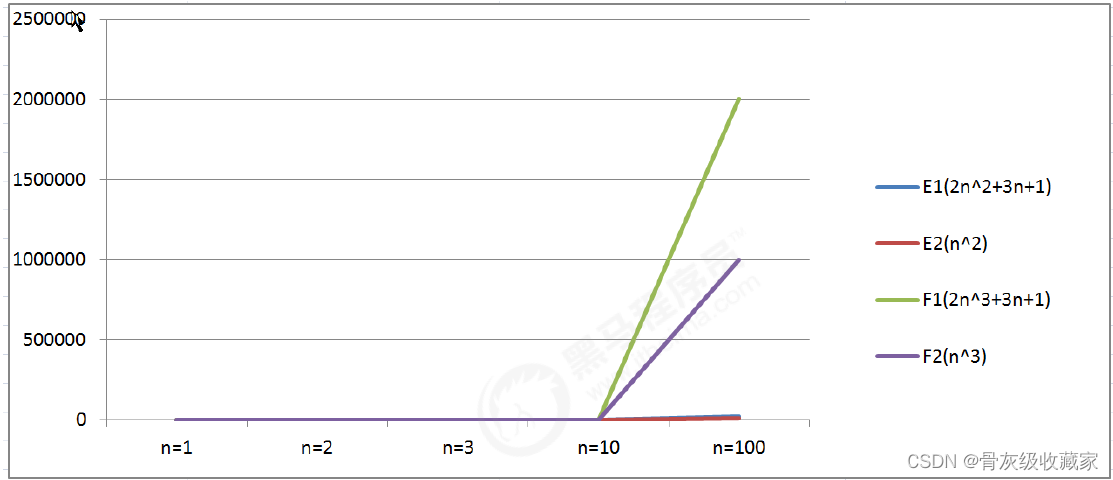 通过数据表格,对比算法E1和算法F1:
通过数据表格,对比算法E1和算法F1:
当n=1时,算法E1和算法F1的执行次数一样;
当n>1时,算法E1的执行次数远远小于算法F1的执行次数;
所以算法E1总体上是由于算法F1的。
通过折线图我们会看到,算法F系列随着n的增长会变得特块,算法E系列随着n的增长相比较算法F来说,变得比较慢,所以可以得出结论:
最高次项的指数大的,随着n的增长,结果也会变得增长特别快
算法时间复杂度
大O记法
定义:
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随着n的变化情况并确定T(n)的量级。算法的时间复杂度,就是算法的时间量度,记作:T(n)=O(f(n))。它表示随着问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称时间复杂度,其中f(n)是问题规模n的某个函数。
在这里,我们需要明确一个事情:执行次数=执行时间
用大写O()来体现算法时间复杂度的记法,我们称之为大O记法。一般情况下,随着输入规模n的增大,T(n)增长最
慢的算法为最优算法。
下面我们使用大O表示法来表示一些求和算法的时间复杂度:
算法一:
public static void main(String[] args) {
int sum = 0;//执行1次
int n=100;//执行1次
sum = (n+1)*n/2;//执行1次
System.out.println("sum="+sum);
}算法二:
public static void main(String[] args) {
int sum = 0;//执行1次
int n=100;//执行1次
for (int i = 1; i <= n; i++) {
sum += i;//执行了n次
}
System.out.println("sum=" + sum);
}public static void main(String[] args) {
int sum=0;//执行1次
int n=100;//执行1次
for (int i = 1; i <=n ; i++) {
for (int j = 1; j <=n ; j++) {
sum+=i;//执行n^2次
}
}
System.out.println("sum="+sum);
}如果忽略判断条件的执行次数和输出语句的执行次数,那么当输入规模为n时,以上算法执行的次数分别为:
算法一:3次
算法二:n+3次
算法三:n^2+2次
如果用大O记法表示上述每个算法的时间复杂度,应该如何表示呢?基于我们对函数渐近增长的分析,推导大O阶
的表示法有以下几个规则可以使用:
1.用常数1取代运行时间中的所有加法常数;
2.在修改后的运行次数中,只保留高阶项;
3.如果最高阶项存在,且常数因子不为1,则去除与这个项相乘的常数;
所以,上述算法的大O记法分别为:
算法一:O(1)
算法二:O(n)
算法的空间复杂度分析
计算机的软硬件都经历了一个比较漫长的演变史,作为为运算提供环境的内存,更是如此,从早些时候的512k,经
历了1M,2M,4M...等,发展到现在的8G,甚至16G和32G,所以早期,算法在运行过程中对内存的占用情况也是
一个经常需要考虑的问题。我么可以用算法的空间复杂度来描述算法对内存的占用。
java中常见内存占用
1.基本数据类型内存占用情况:

计算机访问内存的方式都是一次一个字节

一个引用(机器地址)需要8个字节表示:
例如: Date date = new Date(),则date这个变量需要占用8个字节来表示
4.创建一个对象,比如new Date(),除了Date对象内部存储的数据(例如年月日等信息)占用的内存,该对象本身也有内存开销,每个对象的自身开销是16个字节,用来保存对象的头信息。
5.一般内存的使用,如果不够8个字节,都会被自动填充为8字节:

6.java中数组被被限定为对象,他们一般都会因为记录长度而需要额外的内存,一个原始数据类型的数组一般需要24字节的头信息(16个自己的对象开销,4字节用于保存长度以及4个填充字节)再加上保存值所需的内存。
算法的空间复杂度
了解了java的内存最基本的机制,就能够有效帮助我们估计大量程序的内存使用情况。
算法的空间复杂度计算公式记作:S(n)=O(f(n)),其中n为输入规模,f(n)为语句关于n所占存储空间的函数。
案例:
对指定的数组元素进行反转,并返回反转的内容。
解法一:
public static int[] reverse1(int[] arr){
int n=arr.length;//申请4个字节
int temp;//申请4个字节
for(int start=0,end=n-1;start<=end;start++,end--){
temp=arr[start];
arr[start]=arr[end];
arr[end]=temp;
}
return arr;
}解法二:
public static int[] reverse2(int[] arr){
int n=arr.length;//申请4个字节
int[] temp=new int[n];//申请n*4个字节+数组自身头信息开销24个字节
for (int i = n-1; i >=0; i--) {
temp[n-1-i]=arr[i];
}
return temp;
}忽略判断条件占用的内存,我们得出的内存占用情况如下:
算法一:
不管传入的数组大小为多少,始终额外申请4+4=8个字节;
算法二:
4+4n+24=4n+28;
根据大O推导法则,算法一的空间复杂度为O(1),算法二的空间复杂度为O(n),所以从空间占用的角度讲,算法一要
优于算法二。
由于java中有内存垃圾回收机制,并且jvm对程序的内存占用也有优化(例如即时编译),我们无法精确的评估一个java程序的内存占用情况,但是了解了java的基本内存占用,使我们可以对java程序的内存占用情况进行估算。
由于现在的计算机设备内存一般都比较大,基本上个人计算机都是4G起步,大的可以达到32G,所以内存占用一般情况下并不是我们算法的瓶颈,普通情况下直接说复杂度,默认为算法的时间复杂度。但是,如果你做的程序是嵌入式开发,尤其是一些传感器设备上的内置程序,由于这些设备的内存很小,一般为几kb,这个时候对算法的空间复杂度就有要求了,但是一般做java开发的,基本上都是服务器开发,一般不存在这样的问题。
相关文章:

全网资料最全Java数据结构与算法-----算法分析
算法分析 研究算法的最终目的就是如何花更少的时间,如何占用更少的内存去完成相同的需求,并且也通过案例演示了不同算法之间时间耗费和空间耗费上的差异,但我们并不能将时间占用和空间占用量化,因此,接下来我们要学习…...

【封装xib补充 Objective-C语言】
一、那么首先,咱们就从这个结果来分析 1.就不给大家一步一步分析了,直接分析我们这里怎么想的, 首先,我们看到这样的一个界面,我们想,这些应用数据是不是来源于一个plist文件吧, 所以说,我们首先要,第一步,要懒加载,把这个plist文件中的数据,加载起来, 那么,因…...
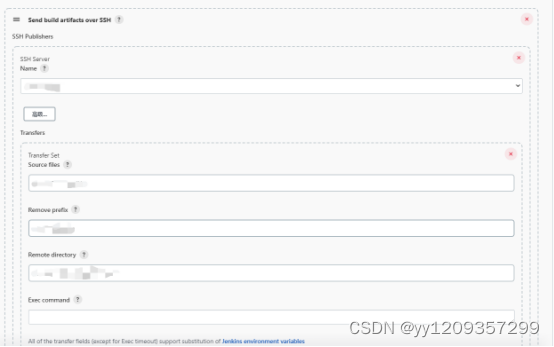
linux + jenkins + svn + maven + node 搭建及部署springboot多模块前后端服务
linux搭建jenkins 基础准备 linux配置jdk、maven,配置系统配置文件 vi /etc/profile配置jdk、maven export JAVA_HOME/usr/java/jdk1.8.0_261-amd64 export CLASSPATH.:$JAVA_HOME/jre/lib/rt.jar:$JAVA_HOME/lib/dt.jar:$JAVA_HOME/lib/tools.jarexport MAVEN_H…...
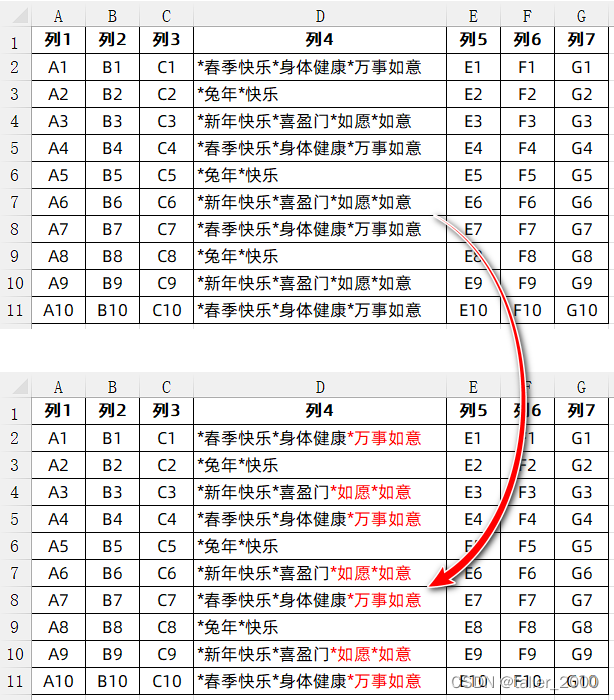
VBA之正则表达式(41)-- 快速标记两个星号之后的字符
实例需求:工作表中的数据保存在A列~G列,现需要识别D列中包含超过两个星号的内容,并将第3个星号及其之后的字符设置为红色字体,如图所示。 示例代码如下。 Sub Demo1()Dim objRegExp As ObjectDim objMatch As ObjectDim strMatch…...

VMware16安装MacOS【详细教程】
安装VMware workstation 双击安装包,然后一直下一步就行了。 进行VMware安装,一直 下一步 在输入产品密钥这一步,如果有查找到可用密钥就填进去,没有就跳过,进入软件后也能输入密钥的。 输入密钥。 最后一步ÿ…...
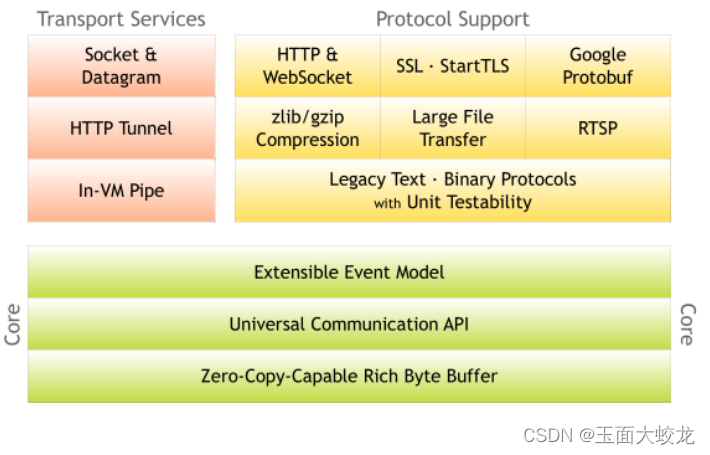
Netty学习(一):Netty概述
一、原生NIO存在的问题 NIO 的类库和API繁杂,使用麻烦:需要熟练掌握Selector、ServerSocketChannel、SocketChannel、ByteBuffer等。需要具备其他的额外技能:要熟悉Java 多线程编程,因为NIO编程涉及到Reactor 模式,你必须对多线程和网络编程…...
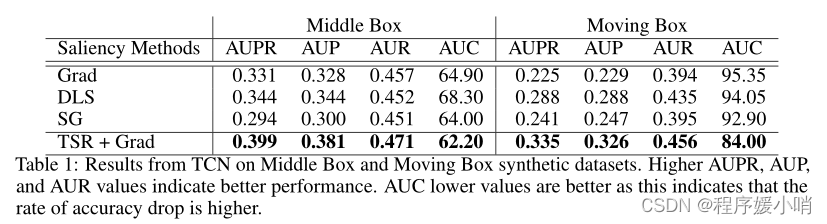
【论文精读】Benchmarking Deep Learning Interpretability in Time Series Predictions
【论文精读】Benchmarking Deep Learning Interpretability in Time Series Predictions Abstract Saliency methods are used extensively to highlight the importance of input features in model predictions. These methods are mostly used in vision and language task…...
自己第一次在虚拟机完整部署ssm项目心得体会
过程使用资源和博文 琳哥发的linux课件文档,阳哥发的linux课件文档(私聊我要) https://www.likecs.com/show-205274015.html https://www.cnblogs.com/aluoluo/articles/15845183.html https://blog.csdn.net/osfipin/article/details/54405445 https://blog.csdn.net/drea…...

操作系统权限提升(二十二)之Linux提权-SUDO滥用提权
系列文章 操作系统权限提升(十八)之Linux提权-内核提权 操作系统权限提升(十九)之Linux提权-SUID提权 操作系统权限提升(二十)之Linux提权-计划任务提权 操作系统权限提升(二十一)之Linux提权-环境变量劫持提权 SUDO滥用提权 SUDO滥用提权原理 sudo是linux系统管理指令&…...

操作系统权限提升(二十四)之Linux提权-明文ROOT密码提权
系列文章 操作系统权限提升(十八)之Linux提权-内核提权 操作系统权限提升(十九)之Linux提权-SUID提权 操作系统权限提升(二十)之Linux提权-计划任务提权 操作系统权限提升(二十一)之Linux提权-环境变量劫持提权 操作系统权限提升(二十二)之Linux提权-SUDO滥用提权 操作系统权限…...

Linux基本命令复习-面试急救版本
1、file 通过探测文件内容判断文件类型,使用权是所有用户, file[options]文件名2、mkdir/rmdir 创建文件目录(文件夹)/删除文件目录 3、grep 指定文件中搜索的特定内容 4、find 通过文件名搜索文件 find name 文件名 5、ps 查…...

随想录二刷Day09——字符串
文章目录字符串1. 反转字符串2. 反转字符串 II3. 替换空格4. 反转字符串中的单词5. 左旋转字符串字符串 1. 反转字符串 344. 反转字符串 思路: 设置两个指针,分别指向字符串首尾,两指针向中间移动,内容交换。 class Solution { …...

正点原子IMX6ULL开发板-liunx内核移植例程-uboot卡在Starting kernel...问题
环境 虚拟机与Linux版本: VMware 17.0.0 Ubuntu16 NXP提供的U-boot与Linux版本: u-boot:uboot-imx-rel_imx_4.1.15_2.1.0_ga.tar.bz2 linux:linux-imx-rel_imx_4.1.15_2.1.0_ga.tar.bz2 开发板: 正点原子-IMX6ULL_EMMC版本,底板版…...
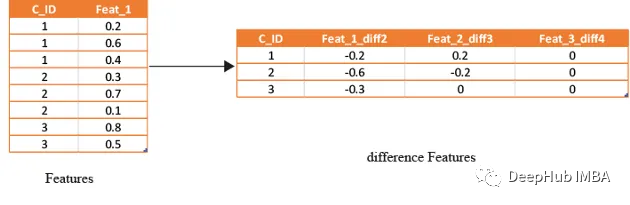
使用手工特征提升模型性能
本文将使用信用违约数据集介绍手工特征的概念和创建过程。 通过对原始数据进行手工的特征工程,我们可以将模型的准确性和性能提升到新的水平,为更精确的预测和更明智的业务决策铺平道路, 可以以前所未有的方式优化模型并提升业务能力。 原始…...
【运维有小邓】Oracle数据库审计
一些机构通常将客户记录、信用卡信息、财务明细之类的机密业务数据存储在Oracle数据库服务器中。这些数据存储库经常因为内部安全漏洞和外部安全漏洞而受到攻击。对这类敏感数据的任何损害都可能严重降低客户对机构的信任。因此,数据库安全性对于任何IT管理员来说都…...

JDK下载安装与环境
🥲 🥸 🤌 🫀 🫁 🥷 🐻❄️🦤 🪶 🦭 🪲 🪳 🪰 🪱 🪴 🫐 🫒 🫑…...

FPGA纯verilog代码实现4路视频缩放拼接 提供工程源码和技术支持
目录1、前言2、目前主流的FPGA图像缩放方案3、目前主流的FPGA视频拼接方案4、本设计方案的优越性5、详细设计方案解读HDMI输入图像缩放图像缓存VGA时序HDMI输出6、vivado工程详解7、上板调试验证8、福利:工程源码获取1、前言 本文详细描述了FPGA纯verilog代码实现4…...
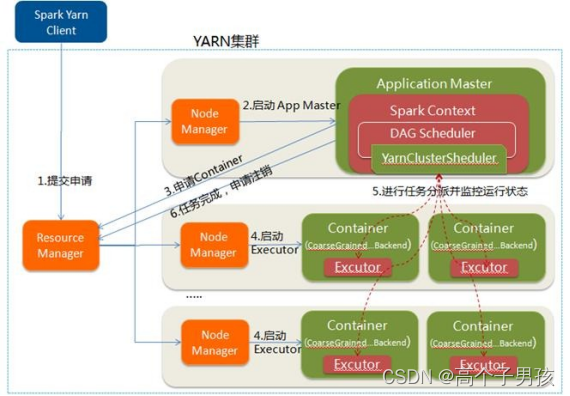
Spark on YARN运行过程,YARN-Client和YARN-Cluster
Spark on YARN运行过程 YARN是一种统一资源管理机制,在其上面可以运行多套计算框架。目前的大数据技术世界,大多数公司除了使用Spark来进行数据计算,由于历史原因或者单方面业务处理的性能考虑而使用着其他的计算框架,比如MapRed…...
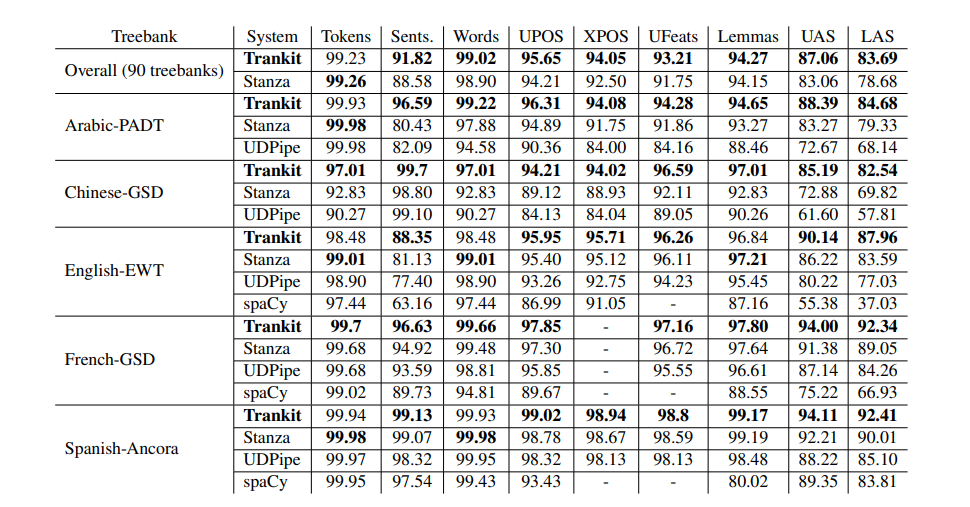
NLP中一些工具列举
文章目录StanfordcoreNLPStanzaTankitspaCySuPar总结StanfordcoreNLP 这个老早就出来了,用java写的,但是已经有很多比他效果好的了。 Stanza 2020ACL发表的,看名字就知道和上一个是同一家的。 用已经切好词的句子进行依存分析。 这个功能…...

面试官:给你一段有问题的SQL,如何优化?
大家好,我是飘渺!我在面试的时候很喜欢问候选人这样一个问题:“你在项目中遇到过慢查询问题吗?你是怎么做SQL优化的?”很多时候,候选人会直接跟我说他们在编写SQL时会遵循的一些常用技巧,比如&a…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
