深度学习笔记:神经网络权重确定初始值方法
神经网络权重不可为相同的值,比如都为0,因为如果这样网络正向传播输出和反向传播结果对于各权重都完全一样,导致设置多个权重和设一个权重毫无区别。我们需要使用随机数作为网络权重
实验程序
在以下实验中,我们使用5层神经网络,每层神经元个数100,使用sigmoid作为激活函数,向网络传入1000个正态分布随机数,测试使用不同的随机数对网络权重的影响。
# coding: utf-8
import numpy as np
import matplotlib.pyplot as pltdef sigmoid(x):return 1 / (1 + np.exp(-x))def ReLU(x):return np.maximum(0, x)def tanh(x):return np.tanh(x)input_data = np.random.randn(1000, 100) # 1000个数据
node_num = 100 # 各隐藏层的节点(神经元)数
hidden_layer_size = 5 # 隐藏层有5层
activations = {} # 激活值的结果保存在这里x = input_datafor i in range(hidden_layer_size):if i != 0:x = activations[i-1]# 改变初始值进行实验!w = np.random.randn(node_num, node_num) * 1# w = np.random.randn(node_num, node_num) * 0.01# w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)# w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)a = np.dot(x, w)# 将激活函数的种类也改变,来进行实验!z = sigmoid(a)# z = ReLU(a)# z = tanh(a)activations[i] = z# 绘制直方图
for i, a in activations.items():plt.subplot(1, len(activations), i+1)plt.title(str(i+1) + "-layer")if i != 0: plt.yticks([], [])# plt.xlim(0.1, 1)# plt.ylim(0, 7000)plt.hist(a.flatten(), 30, range=(0,1))
plt.show()
1 标准差为1随机正态

在这一情况下,权重值主要集中于0和1.由于sigmoid在接近0和1时导数趋于0,这一数据分别会导致反向传播中梯度逐渐减小,这一现象称为梯度消失
2 标准差为0.01随机正态

这时神经网络权重集中在0.5附近,此时不会出现梯度消失,但是由于值集中在同一区间,多个神经网络会输出几乎相同的值,使得神经网络表现能力受限(如开头所说)
3 使用Xavier初始值
Xavier初始值为保证各层权重值具有足够广度设计。其推导出的最优初始值为每一层初始权重值是1/√N,其中N为上一层权重个数
使用sigmoid激活函数和Xavier初始值结果:

可以看到此时权重初始值的值域明显大于了之前的取值。Xavier初始值是基于激活函数为线性函数的假设推导出的。sigmoid函数关于(0, 0.5)对称,其在原点附近还不是完美的线性。而tanh函数关于原点对称,在原点附近可以基本近似于直线,其使用Xavier应该会产生更理想的参数值
使用tanh激活函数和Xavier初始值:

ReLU函数的权重设置
ReLU函数有自己独特的默认权重设置,称为He初始值,其公式为2/√N标准差的随机数,N为上一次神经元个数。

在该分布中,各层广度分布基本相同,这使得即使层数加深,也不容易出现梯度消失问题
使用mnist数据集对不同初始化权重方法进行测试:
该程序使用0.01随机正态,Xavier + sigmoid,He + ReLU进行2000轮反向传播,并绘制总损失关于迭代次数图象
# coding: utf-8
import os
import syssys.path.append("D:\AI learning source code") # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000# 1:进行实验的设置==========
weight_init_types = {'std=0.01': 0.01, 'Xavier': 'sigmoid', 'He': 'relu'}
optimizer = SGD(lr=0.01)networks = {}
train_loss = {}
for key, weight_type in weight_init_types.items():networks[key] = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100],output_size=10, weight_init_std=weight_type)train_loss[key] = []# 2:开始训练==========
for i in range(max_iterations):batch_mask = np.random.choice(train_size, batch_size)x_batch = x_train[batch_mask]t_batch = t_train[batch_mask]for key in weight_init_types.keys():grads = networks[key].gradient(x_batch, t_batch)optimizer.update(networks[key].params, grads)loss = networks[key].loss(x_batch, t_batch)train_loss[key].append(loss)if i % 100 == 0:print("===========" + "iteration:" + str(i) + "===========")for key in weight_init_types.keys():loss = networks[key].loss(x_batch, t_batch)print(key + ":" + str(loss))# 3.绘制图形==========
markers = {'std=0.01': 'o', 'Xavier': 's', 'He': 'D'}
x = np.arange(max_iterations)
for key in weight_init_types.keys():plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
plt.show()

在该图象中可以看到,0.01随机正态由于梯度丢失问题,权重更新速率极慢,在2000次迭代中总损失基本没有变化。Xavier和He都正常进行了反向传播得到了更准确的网络参数,其中He似乎学习速率更快一些
相关文章:

深度学习笔记:神经网络权重确定初始值方法
神经网络权重不可为相同的值,比如都为0,因为如果这样网络正向传播输出和反向传播结果对于各权重都完全一样,导致设置多个权重和设一个权重毫无区别。我们需要使用随机数作为网络权重 实验程序 在以下实验中,我们使用5层神经网络…...

关于 python 的异常使用说明 (python 的文件和异常)
文章目录异常1. 处理异常 ZeroDivisionError 异常2. 使用 try-except 代码块3. 使用异常避免崩溃4. else 代码块5. 处理 FileNotFoundError 异常6. 分析文本7. 失败时一声不吭异常 pyhong 使用被异常成为异常的特殊对象来管理程序执行期间发生的错误。 每当发生让 python 不知所…...
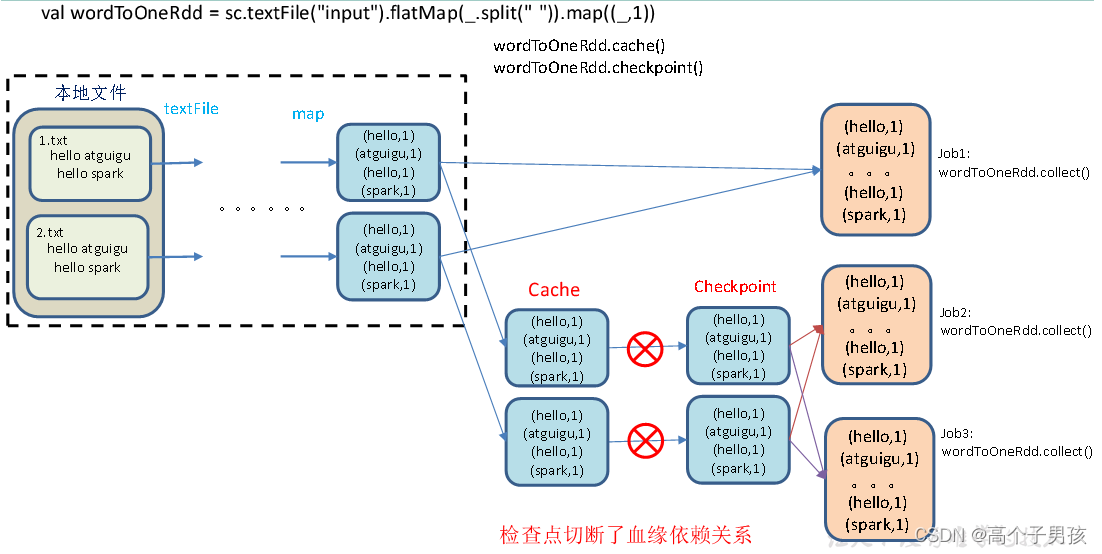
Spark RDD持久化
RDD Cache缓存 RDD通过Cache或者Persist方法将前面的计算结果缓存,默认情况下会把数据以序列化的形式缓存在JVM的堆内存中。但是并不是这两个方法被调用时立即缓存,而是触发后面的action时,该RDD将会被缓存在计算节点的内存中,并供…...

【Linux】Linux系统安装Python3和pip3
1.说明 一般来说Linux会自带Python环境,可能是Python3或者Python2,可能有pip也可能没有pip,所以有时候需要自己安装指定的Python版本。Linux系统下的安装方式都大同小异,基本上都是下载安装包然后编译一下,再创建好软…...

用java进行base64加密
首先定义一组密钥,加密和解密使用同一组密钥private final String key "hahahahahaha";也可以随机生成密钥/*** 生成随机密钥* param keySize 密钥大小推荐128 256* return* throws NoSuchAlgorithmException*/public static String generateSecret(int keySize) th…...
torch函数合集
torch.tensor() 原型:torch.tensor(data, dtypeNone, deviceNone, requires_gradFalse) 功能:其中data可以是:list,tuple,NumPy,ndarray等其他类型,torch.tensor会从data中的数据部分做拷贝(而不是直接引用),根据原始数据类型生成相应类型的torch.Tenso…...

AcWing算法提高课-3.1.2信使
宣传一下算法提高课整理 <— CSDN个人主页:更好的阅读体验 <— 题目传送门点这里 题目描述 战争时期,前线有 nnn 个哨所,每个哨所可能会与其他若干个哨所之间有通信联系。 信使负责在哨所之间传递信息,当然,…...

Paddle OCR Win 11下的安装和简单使用教程
Paddle OCR Win 11下的安装和简单使用教程 对于中文的识别,可以考虑直接使用Paddle OCR,识别准确率和部署都相对比较方便。 环境搭建 目前PaddlePaddle 发布到v2.4,先下载paddlepaddle,再下载paddleocr。根据自己设备操作系统进…...

杂谈:数组index问题和对象key问题
面试题一: var arr [1, 2, 3, 4] 问:arr[1] ?; arr[1] ?答:arr[1] 2; arr[1] 2 这里可以再分为两个问题: 1、数组赋值 var arr [1, 2, 3, 4]arr[1] 10; // 数字场景 arr[10] 1; // 字符串场景 arr[a] 1; // 字符串…...
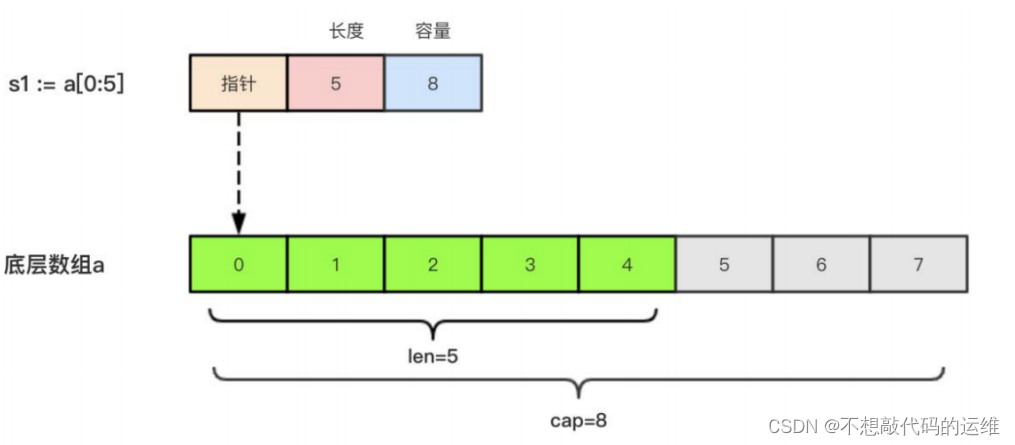
三天Golang快速入门—Slice切片
三天Golang快速入门—Slice切片Slice切片切片原理切片遍历append函数操作切片append添加append追加多个切片中删除元素切片合并string和slice的联系Slice切片 切片原理 由三个部分构成,指针、长度、容量指针:指向slice第一个元素对应的数组元素的地址长…...
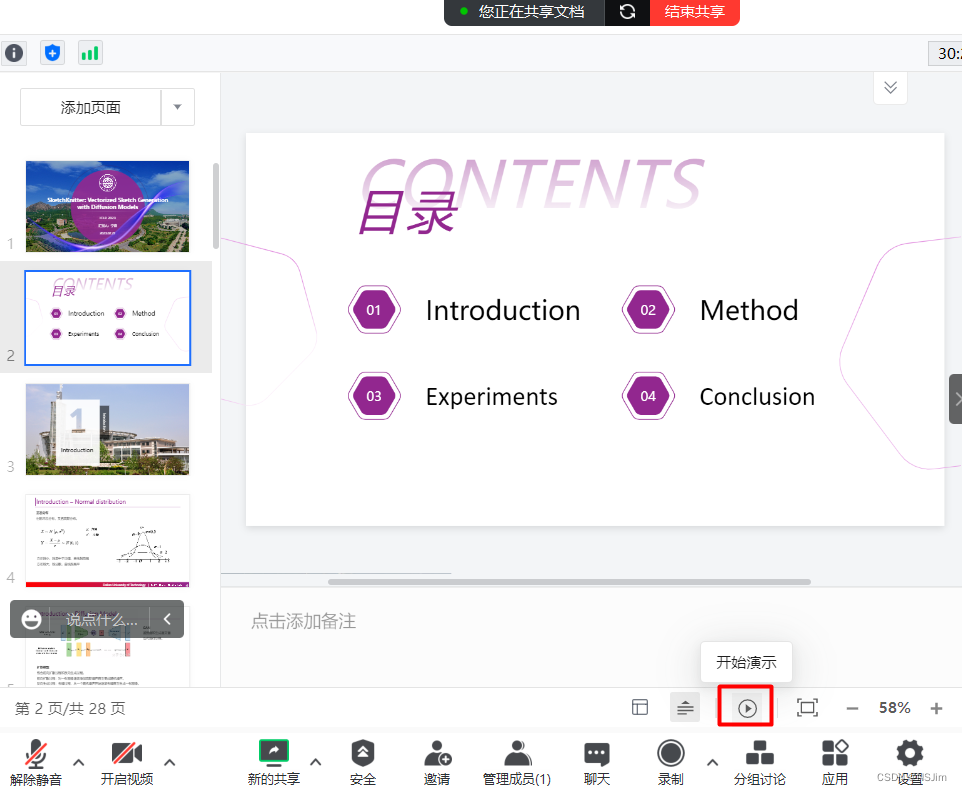
腾讯会议演示者视图/演讲者视图
前言 使用腾讯会议共享PPT时,腾讯会议支持共享用户使用演示者视图/演讲者视图,而会议其他成员可以看到正常的放映视图。下面以Win10系统和Office为例,介绍使用步骤。值得一提的是,该方法同时适用于单显示屏和多显示屏。 腾讯会议…...
【C++】类与对象(一)
文章目录1、面向过程和面向对象初步认识2、类的引入3、类的定义4、类的访问限定符5、类的作用域6、类的实例化7、计算类对象的大小8、this指针9、 C语言和C实现Stack的对比1、面向过程和面向对象初步认识 C语言是面向过程的,关注的是过程,分析出求解问题…...

JavaScript基本语法
本文提到的绝大多数语法都是与Java不同的语法,相同的就不会赘述了.JavaScript的三种引入方式内部js<body><script>alert(hello);</script> </body>行内js<body><div onclick"alert(hello)">这是一个div 点击一下试试</div>…...

OpenCV4.x图像处理实例-道路车辆检测(基于背景消减法)
通过背景消减进行道路车辆检测 文章目录 通过背景消减进行道路车辆检测1、车辆检测思路介绍2、BackgroundSubtractorMOG23、车辆检测实现在本文中,将介绍如何使用简单但有效的背景-前景减法方法执行车辆检测等任务。本文将使用 OpenCV 中使用背景-前景减法和轮廓检测,以及如何…...
pwnlab通关流程
pwnlab通关 关于文件包含,环境变量劫持的一个靶场 信息收集 靶机ip:192.168.112.133 开放端口 根据开放的端口信息决定从80web端口入手 目录信息 在images和upload路径存在目录遍历,config.php被渲染无法查看,upload.php需…...

面向过程与面向对象的区别与联系
目录 什么是面向过程 什么是面向对象 区别 各自的优缺点 什么是面向过程 面向过程是一种以事件为中心的编程思想,编程的时候把解决问题的步骤分析出来,然后用函数把这些步骤实现,在一步一步的具体步骤中再按顺序调用函数。 什么是面向对…...
主机状态(查看资源占用情况、查看网络占用情况)
1. 查看资源占用情况 【1】可以通过top命令查看cpu、内存的使用情况,类似windows的任务管理器 默认5s刷新一次 语法:top 可 Ctrl c 退出 2.磁盘信息监控 【1】使用df命令,查看磁盘信息占用情况 语法:df [ -h ] 以更加人性化…...
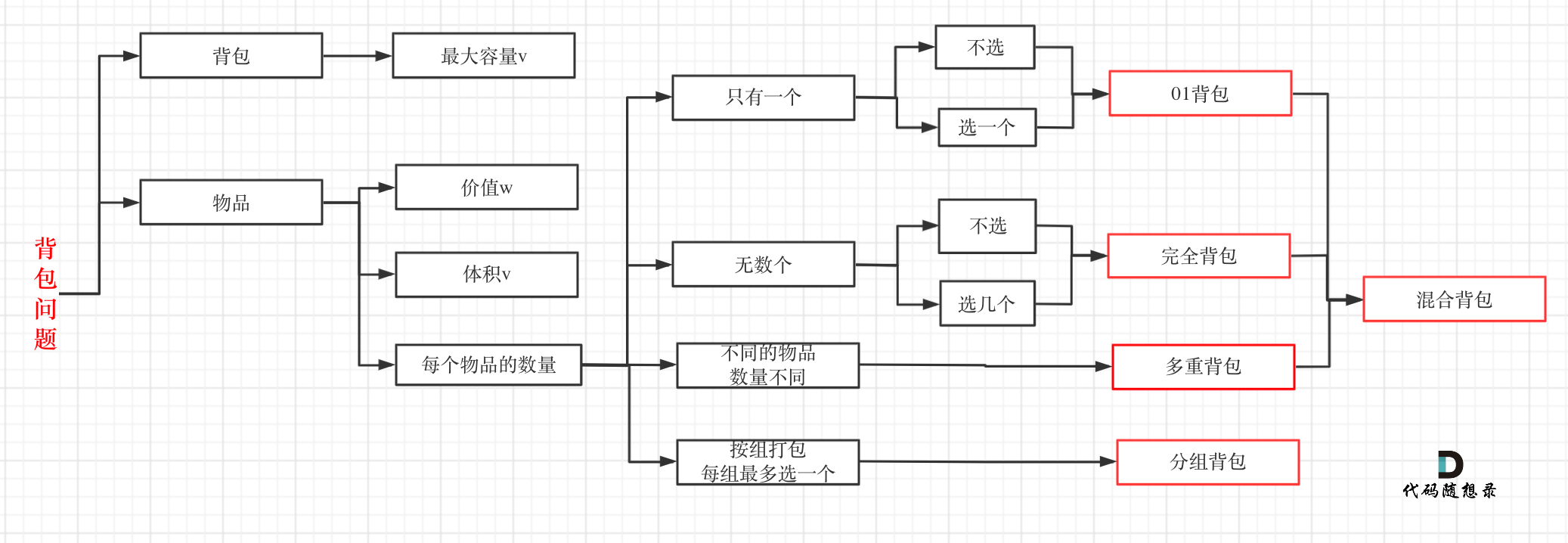
代码随想录算法训练营第四十一天 | 01背包问题-二维数组滚动数组,416. 分割等和子集
一、参考资料01背包问题 二维 https://programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.html 视频讲解:https://www.bilibili.com/video/BV1cg411g7Y6 01背包问题 一维 https://programmercarl.com/%E8%83%8C%E5…...

VMware NSX 4.1 发布 - 网络安全虚拟化平台
请访问原文链接:VMware NSX 4 - 网络安全虚拟化平台,查看最新版。原创作品,转载请保留出处。 作者主页:www.sysin.org VMware NSX 提供了一个敏捷式软件定义基础架构,用来构建云原生应用程序环境。NSX 专注于为具有异…...

计算理论 复杂度预备知识
文章目录计算理论 复杂度预备知识符号递归表达式求解通项公式主方法Akra-Bazzi 定理计算理论 复杂度预备知识 符号 f(n)o(g(n))f(n)o(g(n))f(n)o(g(n)) :∃c\exists c∃c ,当 nnn 足够大时, f(n)<cg(n)f(n)\lt cg(n)f(n)<cg(n) &#…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
