机器学习的复习笔记3-回归的细谈
一、回归的细分
机器学习中的回归问题是一种用于预测连续型输出变量的任务。回归问题的类型和特点如下:
- 线性回归(Linear Regression):线性回归是回归问题中最简单的一种方法。它假设自变量与因变量之间存在线性关系,并通过最小化预测值与真实值之间的差距来拟合最优直线。线性回归易于解释和实现,但对于非线性关系的建模能力有限。
-
多项式回归(Polynomial Regression):多项式回归是在线性回归的基础上引入多项式特征的一种方法。通过添加高次项来拟合更复杂的数据模式,可以更好地适应非线性关系。然而,多项式回归容易出现过拟合问题。
-
岭回归(Ridge Regression):岭回归是一种正则化线性回归方法,通过引入L2正则化项来控制模型的复杂度,防止过拟合。岭回归在特征之间存在共线性(即高度相关)时表现较好。【其核心思想是在最小化残差平方和的同时,加上一个惩罚项,该惩罚项与模型的参数大小有关。这个惩罚项可以将参数的估计值向零进行偏移,从而减少参数估计的方差。具体而言,岭回归使用L2范数作为惩罚项,即将参数的平方和添加到残差平方和中。】
-
Lasso回归(Lasso Regression):Lasso回归是另一种正则化线性回归方法,通过引入L1正则化项来促使模型具有稀疏性,即自动选择对预测目标更重要的特征。Lasso回归可以用于特征选择和降维。
-
弹性网回归(Elastic Net Regression):弹性网回归是岭回归和Lasso回归的结合,既具有L1正则化项的稀疏性特征选择能力,又具有L2正则化项的共线性处理能力。
-
支持向量回归(Support Vector Regression,SVR):支持向量回归是一种非常灵活的回归方法,通过引入核函数将输入空间映射到高维特征空间,从而实现非线性回归。SVR通过定义一个边界带,尽量使观测值落在该带内,同时最小化预测误差。【它基于支持向量机(Support Vector Machine,SVM)的思想,将分类问题扩展到回归问题上。
与传统的回归方法不同,SVR的目标是找到一个边界,使得样本点尽可能地落在该边界内,并且最大化落在边界上的样本之间的间隔。SVR通过引入一个容忍度范围(ε-tube)来容忍落在边界附近的样本点,即允许一部分样本点的预测误差落在容忍度范围内。因此,SVR旨在构建一个能够良好拟合数据并具有较小预测误差的超平面。
SVR的核心思想是通过寻找支持向量来建立回归模型。支持向量是指那些离边界最近的样本点,它们对于构建回归模型具有重要的作用。SVR的目标是找到一个最小化经验风险和模型复杂度的平衡点,从而获得一个效果良好且具有较好泛化能力的回归模型。
SVR可以使用不同的核函数来处理线性和非线性回归问题。常用的核函数包括线性核函数、多项式核函数和高斯径向基核函数等。这些核函数可以将原始样本映射到高维空间,从而使得原本线性不可分的问题在高维空间中变得线性可分。
SVR具有以下特点:SVR可以处理非线性回归问题,并具有较好的泛化能力。SVR通过引入容忍度范围(ε-tube)来允许一定的预测误差,增强了模型对噪声的鲁棒性。
总之,支持向量回归是一种用于解决回归问题的机器学习方法,通过寻找支持向量和引入容忍度范围来建立回归模型,能够处理非线性问题并具有较好的泛化能力。SVR的模型复杂度受支持向量数量的影响,通过选择合适的核函数和正则化参数,可以控制模型的复杂度,避免过拟合。SVR适用于小样本和高维数据的回归问题,具有较好的稳定性和性能。】
【当你无法在平面解决问题,你就要试图提升到空间维度解决问题】
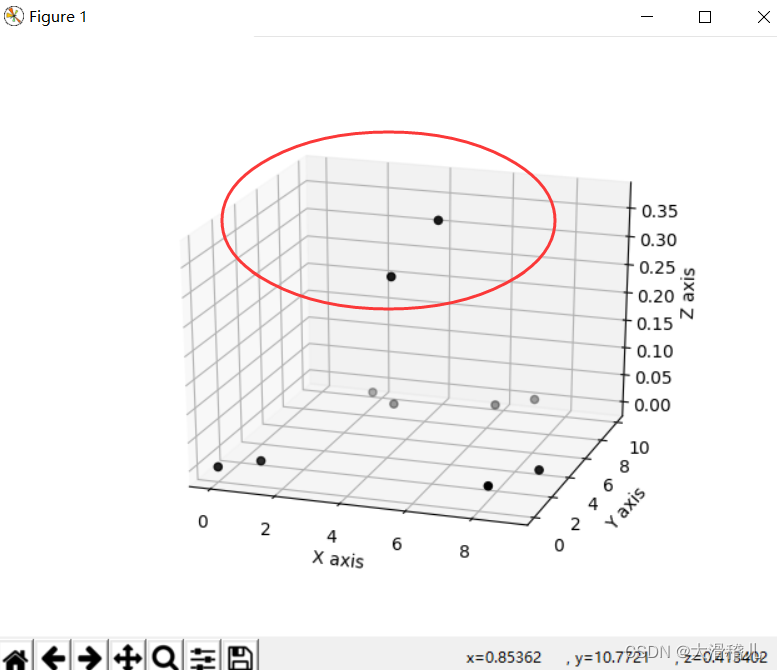
7.决策树回归(Decision Tree Regression):决策树回归使用树结构来建模数据,每个节点代表一个特征变量,每个分叉代表一个判断条件,每个叶节点代表一个输出值。决策树回归具有很好的解释性和非线性建模能力,但容易过拟合。
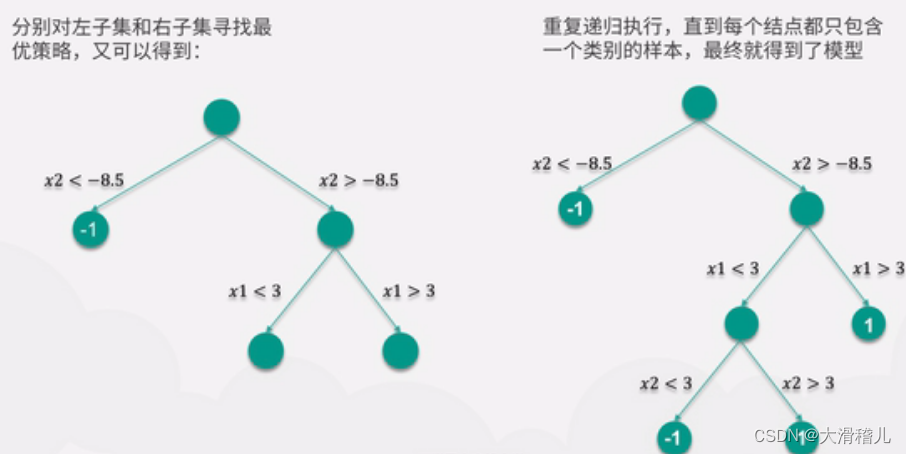
8.随机森林回归(Random Forest Regression):随机森林回归是基于决策树的集成学习方法,通过构建多个决策树并取其平均或投票来进行回归预测。随机森林回归具有较好的鲁棒性和泛化能力,能够处理高维数据和特征选择。【随机森林选取】
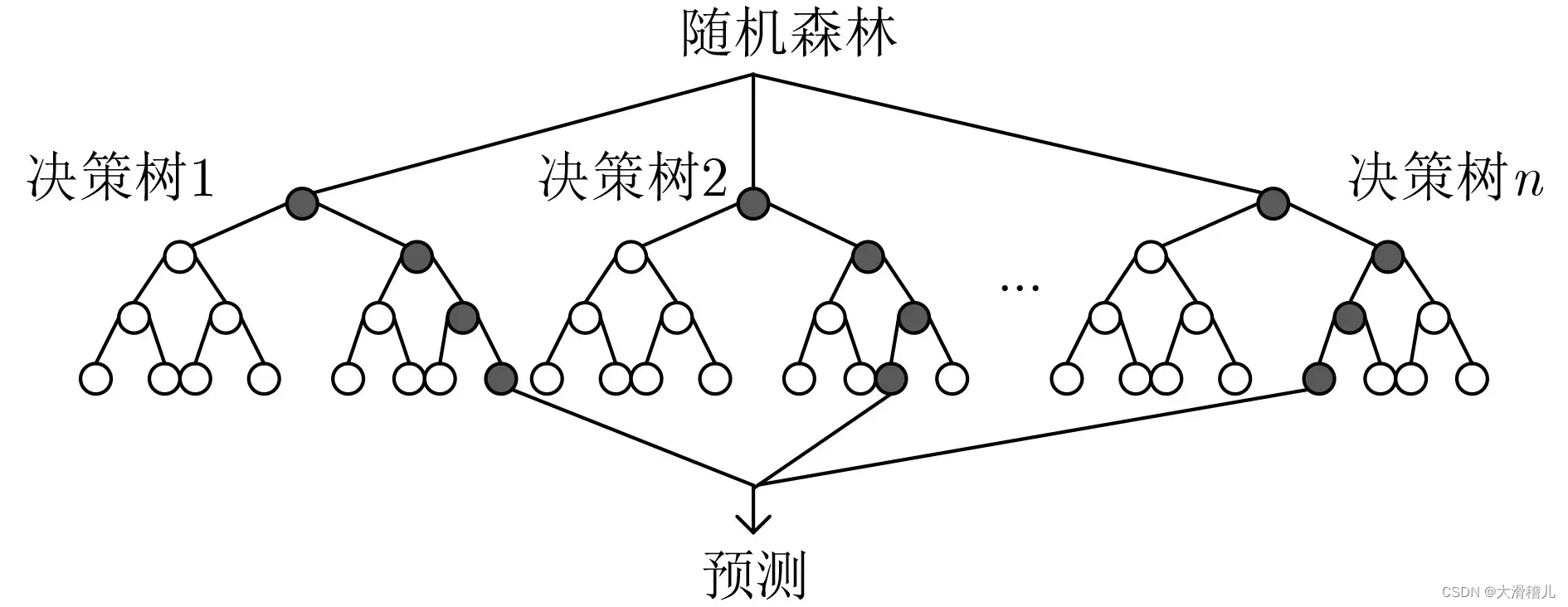
随机森林回归是一种集成学习算法,用于解决回归问题。它结合了决策树和随机性的特点,能够应对高维数据和复杂关系的建模。
随机森林回归的主要步骤如下:
①数据准备:将数据集划分为训练集和测试集,确保数据的质量和完整性。
②随机抽取自助采样集:从训练集中随机有放回地抽取一部分样本,形成一个新的子训练集,样本数与原训练集相同。
③随机选择特征子集:从所有特征中随机选择一部分特征,形成一个新的子特征集。
④构建决策树:使用子训练集和子特征集构建决策树模型。在构建过程中,采用递归的方式选择最佳的划分特征和划分点,直到满足终止条件(如节点中样本数小于某个阈值或达到最大深度)。
④构建多棵决策树:重复步骤2和步骤3,构建多棵决策树形成随机森林。
⑤预测:使用测试集数据,在每棵决策树上进行预测,并取平均值或投票得到最终的预测结果。
随机森林回归具有以下优点:
随机性能够降低过拟合的风险,提高模型的泛化能力。
能够处理高维数据和复杂关系,对异常值和缺失值具有较好的鲁棒性。
能够评估特征的重要性,用于特征选择和特征工程。
相对于单个决策树,随机森林可以更准确地进行预测。
需要注意的是,随机森林回归也有一些限制:
对于具有大量特征和少量样本的问题,可能存在过拟合的情况。
随机森林构建过程中需要消耗较多的计算资源和时间。
随机森林的模型可解释性相对较弱。
9.梯度提升回归(Gradient Boosting Regression):梯度提升回归是一种迭代的集成方法,通过逐步改善残差来拟合模型,并组合多个弱回归器的预测结果。梯度提升回归在回归问题上表现出色,但对于大规模数据集和异常值敏感。
10.神经网络回归(Neural Network Regression):神经网络回归使用多层神经网络来进行回归预测,可以灵活地建模复杂的非线性关系。神经网络回归通常需要大量的数据和计算资源来训练,但可以获得较好的预测性能。
二、回归可以实现分类吗?
机器学习中的回归模型本质上是用于预测连续型输出变量的,而分类则是将样本划分到不同的离散类别中。虽然回归和分类是两个不同的任务,但有一些方法可以通过对回归结果进行适当处理来实现分类。
一种常见的方法是使用阈值(Threshold)来将回归输出转化为二元分类。例如,设定一个阈值,当回归输出大于该阈值时,将样本分类为一类;当回归输出小于等于该阈值时,将样本分类为另一类。这种方法简单直观,但需要合理选择阈值,且不能处理多类分类问题。
另一种方法是使用回归模型的输出概率来进行分类。例如,对于线性回归模型,可以使用逻辑函数(如sigmoid函数)将回归输出映射到[0,1]区间,表示概率。根据概率大小,将样本分配给具有最高概率的类别。这种方法通常被称为逻辑回归,虽然名字中带有"回归",但实际上是一种二元分类算法。
还有一些其他方法,如支持向量回归(SVR)可以通过设置不同的阈值来实现多类分类。随机森林回归和梯度提升回归等集成模型也可以在回归结果的基础上进行分类。这些方法在实践中往往能够拟合非线性的决策边界。
需要注意的是,尽管可以通过适当的处理实现分类,但这样的方法可能无法完全满足分类问题的要求。为了更好地解决分类问题,通常会使用专门设计的分类算法,如逻辑回归、支持向量机、决策树、随机森林和神经网络等。这些算法在设计上更加关注离散类别的划分,具有更好的分类性能。因此,在实际应用中,建议根据具体问题的特点选择适合的分类算法。
相关文章:

机器学习的复习笔记3-回归的细谈
一、回归的细分 机器学习中的回归问题是一种用于预测连续型输出变量的任务。回归问题的类型和特点如下: 线性回归(Linear Regression):线性回归是回归问题中最简单的一种方法。它假设自变量与因变量之间存在线性关系,…...
Git常用命令#切换分支
要在 Git 中切换分支,你可以使用 git checkout 命令。 a.创建新分支并切换到该分支 如果你想要创建一个新分支并立即切换到该分支,可以使用以下命令: git checkout -b 新分支名这会创建一个名为 新分支名 的新分支,并将你的工作目…...

【qml入门教程系列】:qml property使用介绍
作者:令狐掌门 技术交流QQ群:675120140 博客地址:https://mingshiqiang.blog.csdn.net/ 文章目录 属性的定义property基本用法属性变更事件通知属性绑定属性别名只读属性默认属性 default property访问和修改属性方式1:使用setProperty方法方式2:使用QQmlContext设置属性自定…...
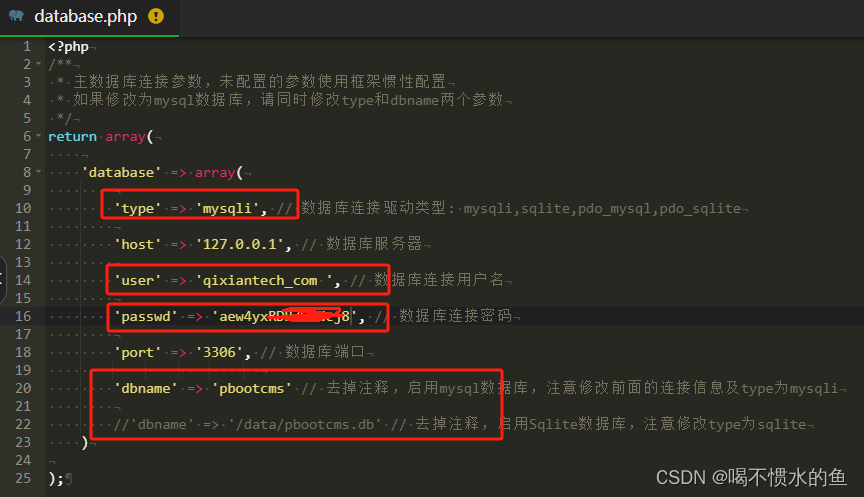
pbootcms建站
pbootcms建站 一、下载pbootcms二、安装1、进入宝塔面在网站栏,新建站点,将该址里面文件全部清再将下载的pbootcms上传至该地址。 三、修改关联数据库1、在根目录下/config打开database.php照如下修改这里我使用mysqli数据库。修改并使用自已创建的数据库…...

Spring的事务传播行为
文章目录 说一下Spring的事务传播行为 今天来和大家聊聊spring中使用的事务传播行为, 说一下Spring的事务传播行为 spring事务的传播行为说的是,当多个事务同时存在的时候,spring如何处理这些事务的行为。 ① PROPAGATION_REQUIRED…...

04_网络编程
网络编程 什么是网络编程 可以让设备中的程序与网络上其他设备中的程序进行数据交互(实现网络通信的) java.net.* 包下提供了网络编程的解决方案 通信的基本架构 CS 架构(Client 客户端 / Server 服务端)BS 架构(…...
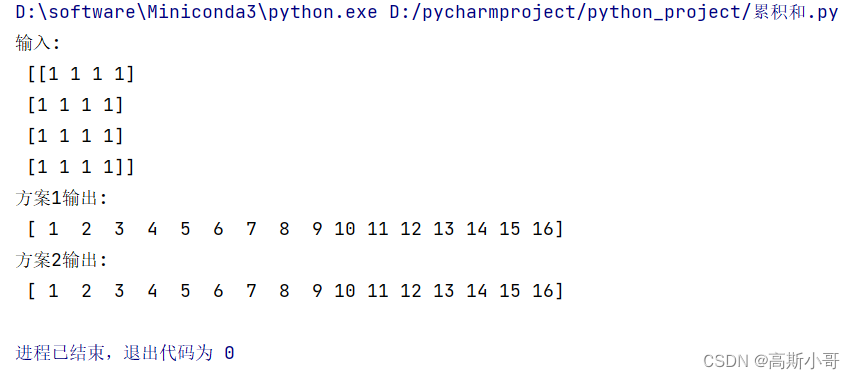
【五分钟】熟练使用numpy.cumsum()函数(干货!!!)
引言 numpy.cumsum()函数用于计算输入数组的累积和。当输入是多维数组时,numpy.cumsum()函数可以沿着指定轴计算累积和。 计算一维数组的累计和 代码如下: # 计算一维数组的累计和 tmp_array np.ones((4,), dtypenp.uint8) # [1, 1, 1, 1] print(&…...
由11月27日滴滴崩溃到近两个月国内互联网产品接二连三崩溃引发的感想
文章目录 知乎文分析微信聊天截图微信公众号 滴滴技术 发文k8s 官方文档滴滴官方微博账号 近两个月国内互联网产品“崩溃”事件2023-10-23 语雀崩溃2023-11-12 阿里云崩溃2023-11-27 滴滴崩溃2023-12-03 腾讯视频崩溃总结 我的感想 知乎文分析 最近连续加班,打车较…...
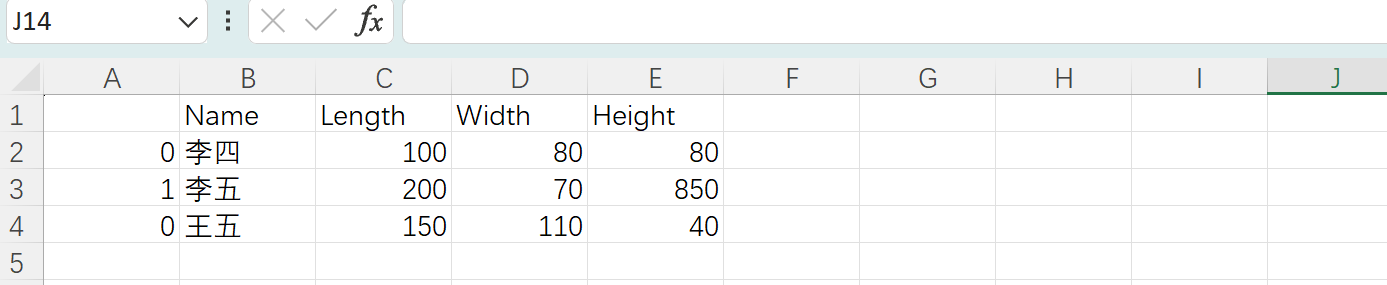
Python按要求从多个txt文本中提取指定数据
基本想法 遍历文件夹并从中找到文件名称符合我们需求的多个.txt格式文本文件,并从每一个文本文件中,找到我们需要的指定数据,最后得到所有文本文件中我们需要的数据的集合 举例 如现有名为file一个文件夹,里面含有大量的.txt格…...
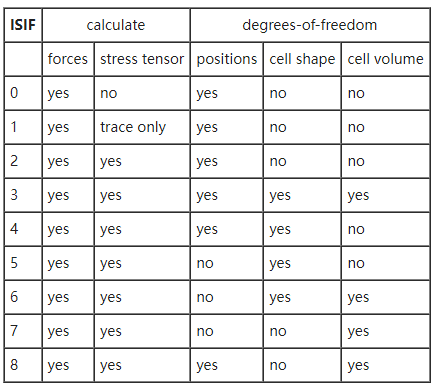
DFT新手教程:VASP中ISIF取值设置
新手初学VASP计算时首先接触到的就是结构优化的计算任务。 在结构优化中,INCAR中的关键参数包括 IBRION ,NSW,ISIF,EDIFF和EDIFFG 各个参数均可在vaspwiki查到可设置的参数以及该参数所具有的设置的含义。 https://www.vasp.at/…...

pytest自动化框架之allure测试报告的用例描述设置
allure测试报告的用例描述相关方法;如下图 allure标记用例级别severity 在做自动化测试的过程中,测试用例越来越多的时候,如果执行一轮测试发现了几个测试不通过,我们也希望能快速统计出缺陷的等级。 pytest结合allure框架可以对…...
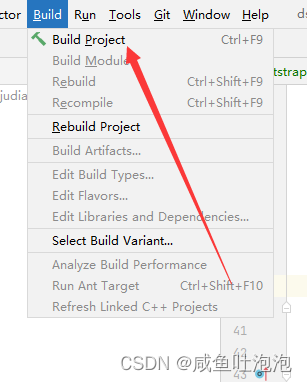
在编程中遇到的问题总结
IDEA空包粘黏问题 创建好目录以后会发现idea自动将空包合并在一起了,而且点击设置里面也没有Compact Middle Package Compact Middle Package如果不在设置的主面板上,则点击Tree Appearance,会发现Compact Middle Package在Tree Appearance里…...
)
【数据库设计和SQL基础语法】--SQL语言概述--SQL的基本结构和语法规则(二)
一、数据控制语言(DCL) 1.1 授权(GRANT) 数据控制语言(DCL)是SQL的一个子集,用于控制数据库中的数据访问和权限。GRANT语句是DCL中的一种,用于向用户或角色授予特定的数据库操作权…...

easyexcel多级表头导出各级设置样式(继承HorizontalCellStyleStrategy实现)
easyexcel多级表头导出各级设置样式(继承HorizontalCellStyleStrategy实现) package com.example.wxmessage.entity;import com.alibaba.excel.metadata.data.WriteCellData; import com.alibaba.excel.write.handler.context.CellWriteHandlerContext;…...

QMLfor python pyside6
QML QML是一种用于创建用户界面的声明性语言,它是Qt生态系统中的一部分。QML使用JavaScript语言和其独特的语法来定义用户界面组件,使得开发人员可以轻松地创建现代化、漂亮而又响应迅速的应用程序。 QML是基于QtQuick技术构建的,QtQuick是…...
几何教学工具 Sketchpad几何画板 mac软件特色
Sketchpad几何画板 for Mac是一款适用于macOS系统的几何教学工具,用户可以在其画板上进行各种几何图形的绘制、演示,帮助教师了解学生的思路和对概念的掌握程度。此外,Sketchpad更深层次的功能则是可以用来进行几何交流、研究和讨论ÿ…...
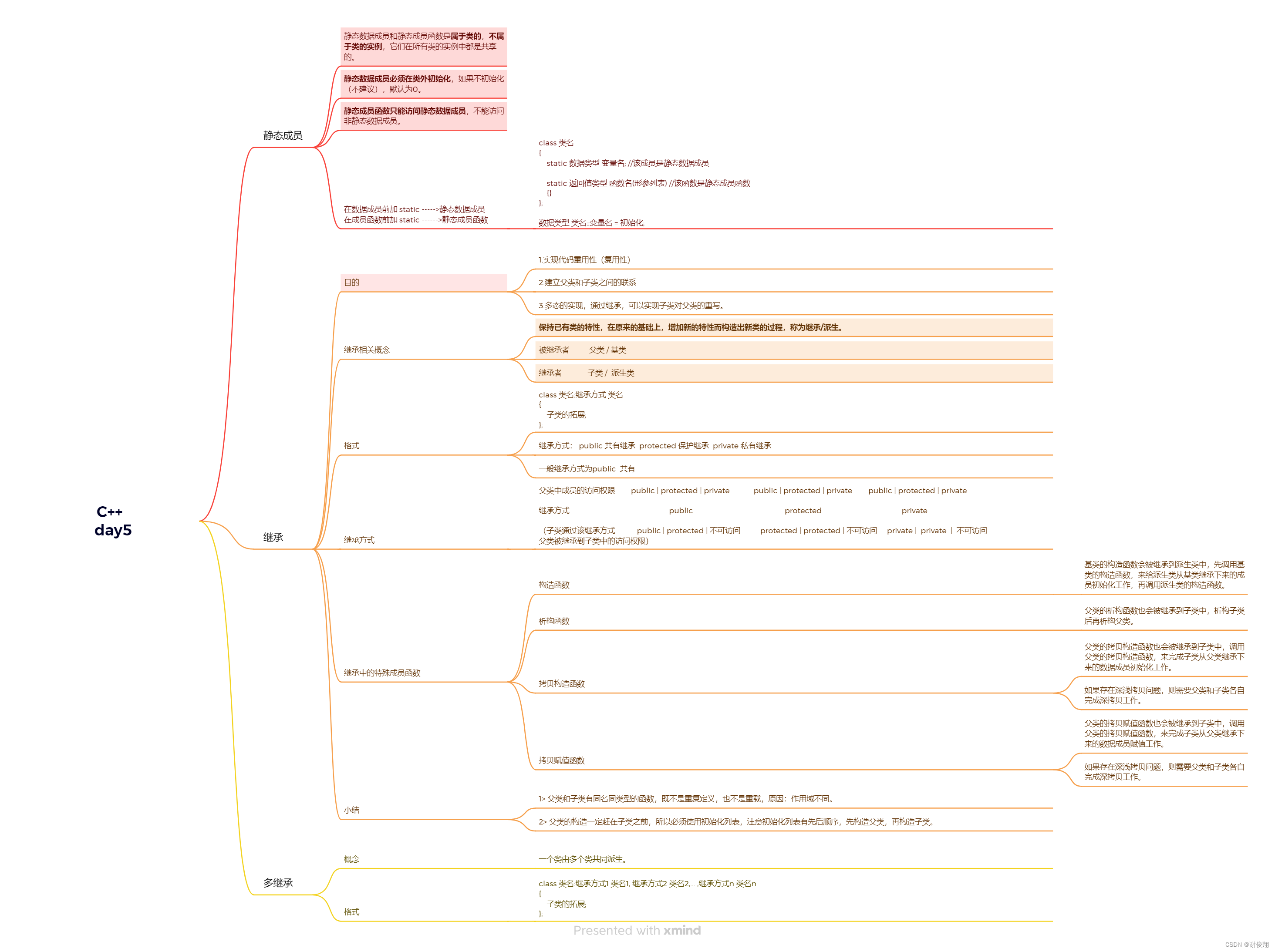
华清远见嵌入式学习——C++——作业5
作业要求: 代码: #include <iostream>using namespace std;//沙发 类 class Sofa { private:string sitting; //是否可坐double *cost; //花费 public://无参构造函数Sofa(){}//有参构造函数Sofa(string s,double c):sitting(s),cost(new double(…...

Java中的类与类之间的关系
1、Java中类与类之间的关系 依赖(Dependency):一个类依赖于另一个类的定义。这种关系通常通过在一个类的方法中创建另一个类的实例来实现。依赖关系是类与类之间最基本的关系之一。关联(Association):关联…...
全新仿某度文库网站源码/在线文库源码/文档分享平台网站源码/仿某度文库PHP源码
源码简介: 全新仿某度文库网站源码/在线文库源码,是以phpMySQL开发的,它是仿某度文库PHP源码。有功能免费文库网站 文档分享平台 实现文档上传下载及在线预览。 仿百度文库是一个以phpMySQL进行开发的免费文库网站源码。仿某度文库实现文档…...

HTTPS的安全问题及应对方案
HTTPS是一种在网络通信中广泛使用的安全协议,通过使用SSL/TLS加密来保护数据的传输。然而,即使在使用了HTTPS的情况下,仍然存在一些潜在的安全问题。本文将深入探讨HTTPS的安全问题,并提供一些有效的应对策略,以确保数…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
