【每日一题】从二叉搜索树到更大和树
文章目录
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:中序遍历的反序
- 方法二:后缀数组
- 写在最后
Tag
【中序遍历】【二叉树】【2023-12-04】
题目来源
1038. 从二叉搜索树到更大和树
题目解读
在二叉搜索树中,将每一个节点的值替换成树中大于等于该节点值的所有节点值之和。
解题思路
方法一:中序遍历的反序
前言
给的是一棵二叉搜索树(英文名称为 Binary Search Tree,以下简称为 BST),我们要充分利用 BST 的性质来解题。BST 的约束条件为:
- 节点的左子树的节点值都小于该节点的值;
- 节点的右子树的节点值都大于该节点的值;
- 左右子树也都是 BST。
根据 BST 的约束条件可以得到一条重要的性质:如果对 BST 进行中序遍历,那么将会得到 BST 中节点值升序的一个序列。
思路
我们以示例 1 为例来说明我们是如何利用 BST 的性质来解决本题的。
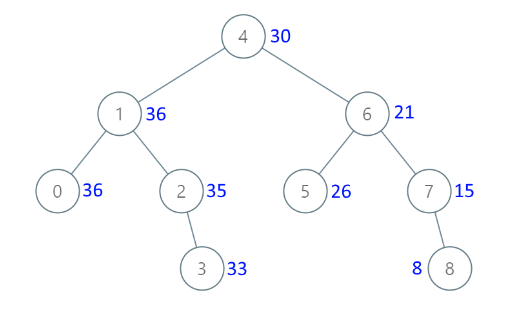
比如,为了计算根节点修改后的值,应该先遍历右子树的所有节点,因为 BST 的右子树的节点值都大于根节点的值,得有所有右子树的节点值之后,再加上根节点的值,即
8 + 7 + 6 + 5 + 4 = 30 8+7+6+5+4=30 8+7+6+5+4=30
这便是根节点修改后的值。我们在计算某个节点(后文称之为 “计算节点”)的大于等于该节点的所有节点之和是利用递归来实现的。
“递”:一直 “递” 到叶子节点,也就是到达了递归边界。
“归”:在归的过程中自底向上的将叶子节点到 “计算节点” 这一路上的所有节点值都修改了,修改为递归上来的 s(当前节点的右子树的所有节点之和)加上当前节点的值。
在更新了 “计算节点” 的值之后,递归修改 “计算节点” 的左子树。
算法
初始化全局变量 s = 0,从根节点开始递归修改,递归函数为:
- 递归出口为当前节点到达了叶子节点即
node == nullptr; - 递归修改右子树;
- 把当前节点的值加到
s中,接着修改当前节点的值; - 递归修改左子树。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private: int s = 0;void dfs(TreeNode* node) {if (node == nullptr) {return;}dfs(node->right);s += node->val;node->val = s;dfs(node->left);}public:TreeNode* bstToGst(TreeNode* root) {dfs(root);return root;}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n), n n n 为 BST 的节点个数。
空间复杂度: O ( n ) O(n) O(n),最坏情况下,BST 退化成一条链,此时递归需要的栈空间为 O ( n ) O(n) O(n)。
方法二:后缀数组
熟悉 “如果对 BST 进行中序遍历,那么将会得到 BST 中节点值升序的一个序列” 这条性质的读者还可以有另一种解题思路。
首先将 BST 按中序遍历的顺序输出到数组中,得到升序数组 nums。数组中的数加上其后的所有数之和就是 BST 中的 “大于等于该节点值的所有节点值之和”。
于是需要维护一个后缀数组,最后将更新好的后缀数组中的值还原到二叉搜索树上。
该方法实现起来有些繁琐,感兴趣的读者可以自行实现。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【每日一题】从二叉搜索树到更大和树
文章目录 Tag题目来源题目解读解题思路方法一:中序遍历的反序方法二:后缀数组 写在最后 Tag 【中序遍历】【二叉树】【2023-12-04】 题目来源 1038. 从二叉搜索树到更大和树 题目解读 在二叉搜索树中,将每一个节点的值替换成树中大于等于该…...
@Scheduled,Quartz,XXL-JOB三种定时任务总结
Scheduled,Quartz,XXL-JOB三种定时任务总结 一、Scheduled 简介 Scheduled 是 Spring 框架中用于声明定时任务的注解。通过使用 Scheduled 注解,你可以指定一个方法应该在何时执行,无需依赖外部的调度器。 这个注解通常与Enab…...

开会做笔记的时候用什么软件比较好?
在工作生涯中,会经历很多大大小小的会议,而如何快速准确记录下会议上重要的内容,成了很多上班族的必修课。在会上做笔记,选择什么样的工具才能事半功倍,成了一个值得深思的问题。而经过一段时间的测评后,我…...
HTML CSS JavaScript的网页设计
一、网页界面效果: 二、HTML代码: <!DOCTYPE html> <!-- 声明文档类型--> <html lang"en"> …...
37.从0到上线三天搭建个人网站(第一天)
点赞收藏加关注,你也能住大别墅! 挑战三天搭建个人网站 从0到上线 一、项目的主要功能 1.作为自己在网上的一个工作室。 2.发帖 3.展示个人项目连接 4.介绍自己(没准儿还能接点活儿) 二、UI风格参考 三、技术选型 1.前端&a…...

室内外融合便携式定位终端5G+UWB+RTK
一、介绍 便携式定位终端主要用于提供高精度的位置数据,支持室内UWB定位和室外北斗系统定位功能,支持5G公网和5G专网通信功能,便携式定位终端中超宽带(UWB)和实时动态(RTK)技术的集成代表了精确位置跟踪方面的重大进步。这款UWBRTK便携式定位…...

使用Java语言判断一个数据类型是奇数还是偶数
判断一个数字类型是奇数,还是偶数,只需要引入Scanner类,然后按照数据类型的定义方式进行定义,比较是按照与2进行整除后的结果;如果余数为零,则代表为偶数,否则为奇数。 import java.util.Scann…...
Java三种代理模式:静态代理、动态代理和CGLIB代理
Java三种代理模式:静态代理、动态代理和CGLIB代理 代理模式 代理模式是23种设计模式种的一种。代理模式是一种结构型设计模式,它允许为其他对象提供一个替代品或占位符,以控制对这个对象的访问。代理模式可以在不修改被代理对象的基础上&am…...
vivado实现分析与收敛技巧9-分析使用率统计数据
实现问题的常见原因之一是未考量显式和隐式物理约束。例如 , 管脚分配 (pinout) 在逻辑布局上变为显式物理约束。 slice( 分片 ) 逻辑在大部分器件中都是一致的。但如下专用资源表示的是隐式物理约束 , 因为这些资源仅在某些位置…...
7nm项目之顶层规划——01数据导入
1.创建workspace 创建workspace后,在其目录下产生。 CORTEXA53.json文件是将有默认配置的文件master.json、有library的.config.json文件、tunes下CORTEXA53.tunes.json文件合并 注:tunes下的CORTEXA53.tunes.json文件可以覆盖一些master.json的设置…...

一键式紧急报警柱系统
随着科技的不断发展,一键式紧急报警柱在我们的生活和工作中扮演着越来越重要的角色。在这篇文章中,我们将一起探究与一键式紧急报警柱有关的知识。 一键式紧急报警柱是一种常见的安全防护设备,能够在紧急情况下快速发出警报,保护…...

4-Docker命令之docker run
1.docker run介绍 docker run命令是用来创建新的容器并运行相关命令 2.docker run用法 docker run [参数] [root@centos79 ~]# docker run --helpUsage: docker run [OPTIONS] IMAGE [COMMAND] [ARG...]Create and run a new container from an imageAliases:docker conta…...
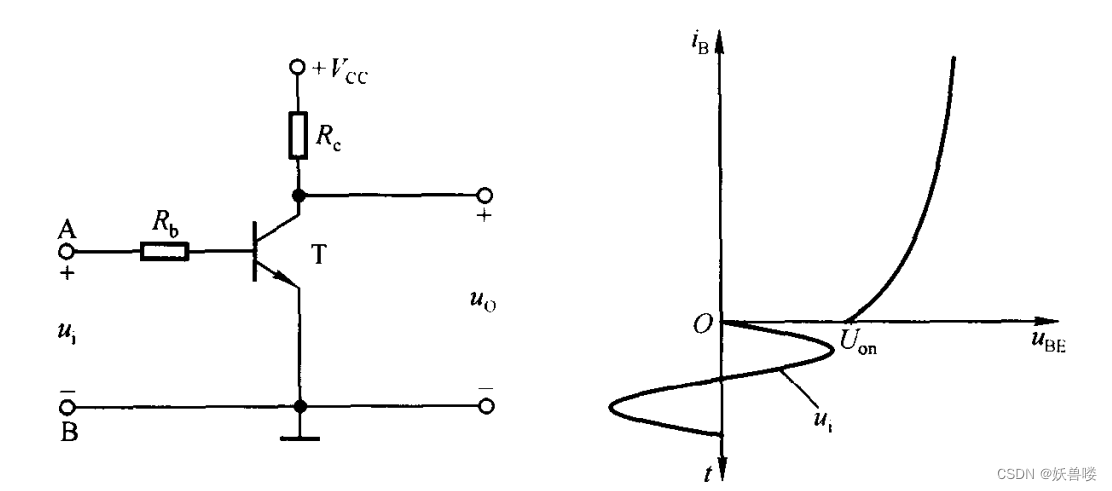
【模电】直流通路与交流通路
直流通路与交流通路 通常,在放大电路中,直流电源的作用和交流信号的作用总是共存的,即静态电流、电压和动态电流、电压总是共存的。但是由于电容、电感等电抗元件的存在,直流量所流经的通路与交流信号所流经的通路不完全相同。因此…...

SpringBoot JprotoBuf序列化与反序列化的实现
文章目录 前言一、protobuf与JprotoBufprotobuf介绍JprotoBuf介绍protobuf与JprotoBuf的区别二、JprotoBuf特点三、类型转换对照表四、ProtobufClass编写五、序列化与反序列化测试六、使用JprotoBuf时的注意事项七、JprotoBuf与protobuf序列化反序列化结果比较前言 在软件开发…...

互联网Java工程师面试题·Spring Boot篇·第一弹
目录 1、什么是 Spring Boot? 2、Spring Boot 有哪些优点? 3、什么是 JavaConfig? 4、如何重新加载 Spring Boot 上的更改,而无需重新启动服务器? 5、Spring Boot 中的监视器是什么? 6、如何在 Sprin…...

HostHunter虚拟主机发现
HostHunter虚拟主机发现 1.HostHunter2.安装3.参数解释4.实例1.HostHunter HostHunter 一种工具,用于有效发现和提取提供大量目标 IPv4 或 IPv6 地址的主机名。HostHunter 利用简单的 OSINT 和主动协调技术将 IP 目标与虚拟主机名进行映射。这对于发现组织的真正攻击面特别有…...

鸿蒙开发:UIAbility组件间交互探索实战【鸿蒙专栏-22】
UIAbility组件间交互(设备内) 在设备内,UIAbility(用户界面能力)是系统调度的最小单元,它们负责展示用户界面和执行相关的业务逻辑。设备内的不同功能模块之间的交互是应用程序开发中的重要部分。本文将探讨设备内UIAbility之间的交互方式,包括启动应用内的UIAbility、…...
VSCode Vue 开发环境配置
Vue是前端开发中的重要工具与框架,可以保住开发者高效构建用户界面。 Vue2官方文档:https://v2.cn.vuejs.org/ Vue3官方文档:https://cn.vuejs.org/ Vue的安装和引用 Vue2的官方安装指南:https://v2.cn.vuejs.org/v2/guide/ins…...

clickhouse从mysql同步数据到clickhouse的几种方式
背景 我们的业务数据一般来说都是放在Mysql中的,而我们要分析的数据一般都存放在clickhouse中,所以如何把数据从mysql同步到ck,就变成了一个必须的步骤,本文简单记录下几种同步的方式 mysql数据同步到clickhouse 方式一&#x…...

“滑动窗口”算法实例
1 问题 给定一个字符串“S”,找出其中不含有重复字符的最长子串的长度。例如:S‘ABCABCBB’,则不含重复字符的最长字串长度为3.。S‘ABCDFG’,则不含重复字符的最长字串长度为6。要求设计一个Python程序实现该功能? 2 方法 按照一…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...

更新 Docker 容器中的某一个文件
🔄 如何更新 Docker 容器中的某一个文件 以下是几种在 Docker 中更新单个文件的常用方法,适用于不同场景。 ✅ 方法一:使用 docker cp 拷贝文件到容器中(最简单) 🧰 命令格式: docker cp <…...

篇章一 论坛系统——前置知识
目录 1.软件开发 1.1 软件的生命周期 1.2 面向对象 1.3 CS、BS架构 1.CS架构编辑 2.BS架构 1.4 软件需求 1.需求分类 2.需求获取 1.5 需求分析 1. 工作内容 1.6 面向对象分析 1.OOA的任务 2.统一建模语言UML 3. 用例模型 3.1 用例图的元素 3.2 建立用例模型 …...
