LeetCode-470. 用 Rand7() 实现 Rand10()【数学 拒绝采样 概率与统计 随机化】
LeetCode-470. 用 Rand7 实现 Rand10【数学 拒绝采样 概率与统计 随机化】
- 题目描述:
- 解题思路一:首先说一个结论就是`(rand_X() - 1) × Y + rand_Y() ==> [1,X*Y]`,即可以等概率的生成[1, X * Y]范围的随机数,其实就像军训的时候报数,Y是每一行的人数,X是列数【参考下面的图】。第二就是拒绝采样,效果是能够减少调用rand7()的调用次数。我们在利用`(rand_7() - 1) × 7 + rand_7() ==> [1,7*7]`得到rand49()的时候,我们希望能够等概率的生成[1,10]的随机数,那么可以拒绝掉大于40的数。即`if num<=40:`才进行采样。
- 解题思路二:0
- 解题思路三:0
题目描述:
给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数,试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数。
你只能调用 rand7() 且不能调用其他方法。请不要使用系统的 Math.random() 方法。
每个测试用例将有一个内部参数 n,即你实现的函数 rand10() 在测试时将被调用的次数。请注意,这不是传递给 rand10() 的参数。
示例 1:
输入: 1
输出: [2]
示例 2:
输入: 2
输出: [2,8]
示例 3:
输入: 3
输出: [3,8,10]
提示:
1 <= n <= 105
进阶:
rand7()调用次数的 期望值 是多少 ?
你能否尽量少调用 rand7() ?
解题思路一:首先说一个结论就是(rand_X() - 1) × Y + rand_Y() ==> [1,X*Y],即可以等概率的生成[1, X * Y]范围的随机数,其实就像军训的时候报数,Y是每一行的人数,X是列数【参考下面的图】。第二就是拒绝采样,效果是能够减少调用rand7()的调用次数。我们在利用(rand_7() - 1) × 7 + rand_7() ==> [1,7*7]得到rand49()的时候,我们希望能够等概率的生成[1,10]的随机数,那么可以拒绝掉大于40的数。即if num<=40:才进行采样。

为了充分利用被拒绝的采样结果,即舍弃掉[41, 49]这9个数。我们可以使用a = num - 40得到rand9,从而可以得到(rand_9() - 1) × 7 + rand_7() ==> [1,9*7]得到rand63,从而对rand63进行采样。这样之后的就不难理解了。
# The rand7() API is already defined for you.
# def rand7():
# @return a random integer in the range 1 to 7class Solution:def rand10(self):""":rtype: int"""while True:a = rand7()b = rand7()num = (a-1)*7 + b # rand49if num<=40:return num%10 + 1a = num - 40 # rand9b = rand7()num = (a-1)*7 + b # rand63if num<=60:return num%10 + 1a = num - 60 # rand3b = rand7()num = (a-1)*7 + b # rand21if num<=20:return num%10 + 1
时间复杂度:期望时间复杂度为O(1),但最坏情况下会达到 (∞)(一直被拒绝)。
空间复杂度:O(1)
分析一下rand7()调用次数的 期望值:
首先调用2次得到a,b
然后拒绝采样一次概率是9/49
第二次是9/49 * 3/63
第三次是9/49 * 3/63 * 1/21就是进入下一轮while循环了。所以是一个等比数列。
a = 2 + 9 49 + 9 49 ⋅ 3 63 / / 是每次采样成功的概率 b = 9 49 ⋅ 3 63 ⋅ 1 21 / / 是每次进入下一轮循环的概率(等比数列的公比) E ( # c a l l ) = a ⋅ 1 1 − b ≈ 2.19333 \begin{align} a &= 2 + \frac{9}{49}+\frac{9}{49}·\frac{3}{63} \quad // \text{是每次采样成功的概率} \notag \\ b &= \frac{9}{49}·\frac{3}{63}·\frac{1}{21} \quad // \text {是每次进入下一轮循环的概率(等比数列的公比)} \notag \\ E(\#call) &= a·\frac{1}{1-b} \notag \\ &\approx 2.19333 \end{align} abE(#call)=2+499+499⋅633//是每次采样成功的概率=499⋅633⋅211//是每次进入下一轮循环的概率(等比数列的公比)=a⋅1−b1≈2.19333
所以期望次数是2.19332
解题思路二:0
解题思路三:0
相关文章:

LeetCode-470. 用 Rand7() 实现 Rand10()【数学 拒绝采样 概率与统计 随机化】
LeetCode-470. 用 Rand7 实现 Rand10【数学 拒绝采样 概率与统计 随机化】 题目描述:解题思路一:首先说一个结论就是(rand_X() - 1) Y rand_Y() > [1,X*Y],即可以等概率的生成[1, X * Y]范围的随机数,其实就像军训的时候报数…...

通达信指标公式19:龙虎榜股票池——主力控盘度的计算方法
0.小红牛本指标,选股的思路说明:控盘度,又称主力控盘,是指主力控制了某只股票的大部分流通股,从而控制了股票的价格。主力控盘的目的通常是为了获取更多的收益,通过控制股票价格来实现其策略。所以首要分析…...
手搓图片滑动验证码_JavaScript进阶
手搓图片滑动验证码 背景代码效果图展示网站 背景 在做前端项目开发的时候,少不了登录注册部分,既然有登录注册就少不了机器人验证,验证的方法有很多种,比如短信验证码、邮箱验证码、图片滑动、图片验证码等。 由于鄙人在开发中…...

Linux服务器超级实用的脚本
1.使用INOTIFY+RSYNC自动实时同步数据 代码执行: bash inotify_rsyncs.sh :cat inotify_rsyncs.sh 脚本内容如下: #!bing/bash # Author: reyn #检测/data路径下的文件变化,排除Temp目录 INOTIFY_CMD="inotifywait -mrq -e modify,create,move,delete /data/ --exc…...

IntelliJ IDEA安装使用教程#intellij idea
做为基础开发软件,idea、pycharm、phpstorm是高级企业级开发中常用的图形化工具。 安装非常简单:去官网下载即可,有社区版本、有企业版本: IntelliJ IDEA – 领先的 Java 和 Kotlin IDE 因版权问题:这里不方面多讲。…...
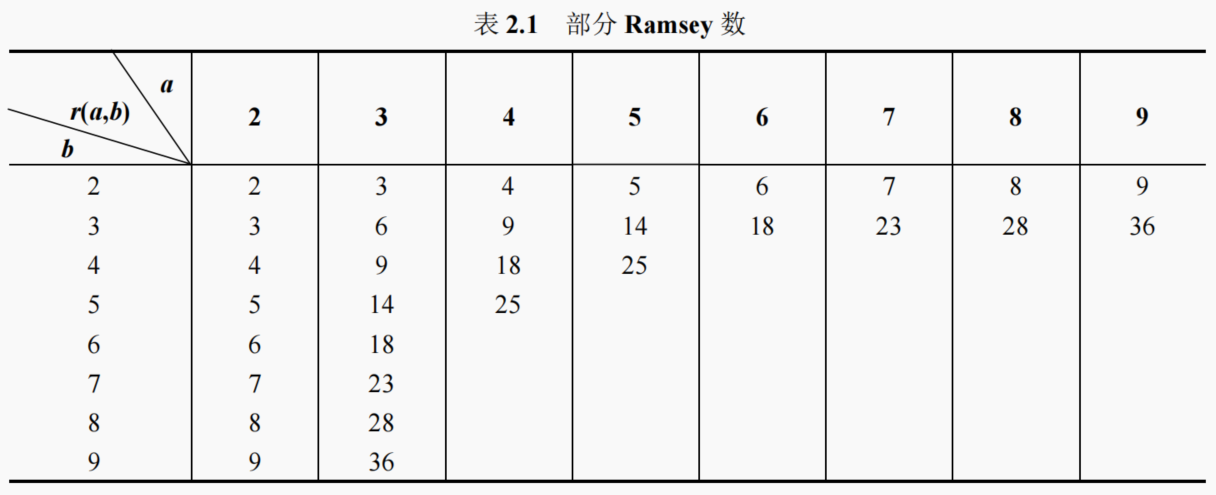
【组合数学】容斥鸽巢原理
目录 1. 容斥原理容斥原理三种形式 2. 容斥原理应用有限重复数的多重集合的 r 组合数错排问题 3. 鸽巢原理4. Ramsey 定理 1. 容斥原理 容斥原理提供了一种通过计算每个单独集合的大小,然后修正重复计数的方法,从而得到多个集合并集大小的计算方法。它通…...
视频后期特效处理软件 Motion 5 mac中文版
Motion mac是一款运动图形和视频合成软件,适用于Mac OS平台。 Motion mac软件特点 - 精美的效果:Motion提供了多种高质量的运动图形和视频效果,例如3D效果、烟雾效果、粒子效果等,方便用户制作出丰富多彩的视频和动画。 - 高效的工…...

【智能家居】一、工厂模式实现继电器灯控制
用户手册对应的I/O 工厂模式实现继电器灯控制 代码段 controlDevice.h(设备设备)main.c(主函数)bathroomLight.c(浴室灯)bedroomLight.c(卧室灯)restaurantLight.c(餐厅…...
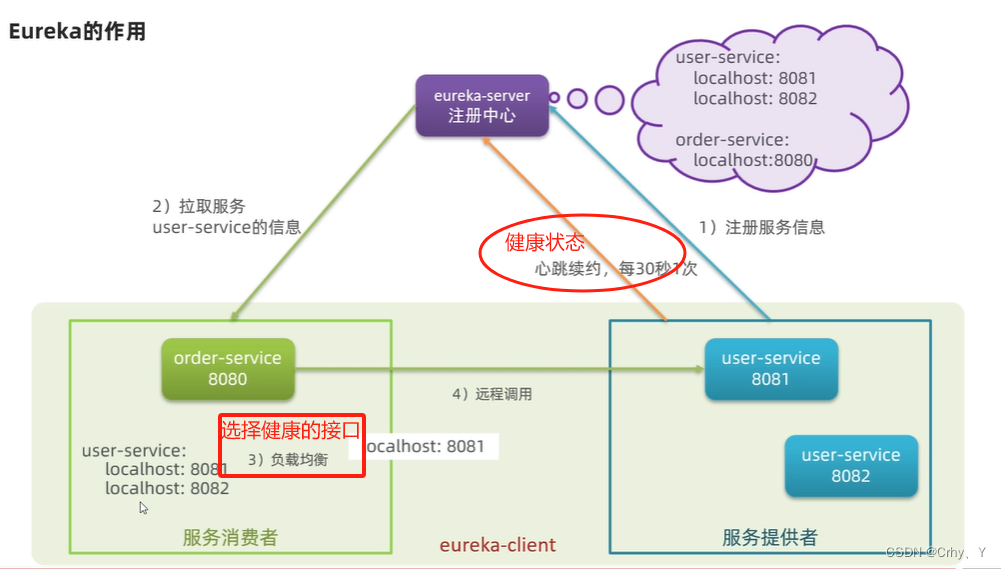
第三节:提供者、消费者、Eureka
一、 提供者 消费者(就是个说法、定义,以防别人叭叭时听不懂) 服务提供者:业务中被其他微服务调用的服务。(提供接口给其他服务调用)服务消费者:业务中调用其他微服务的服务。(调用…...
Leetcode刷题详解——等差数列划分
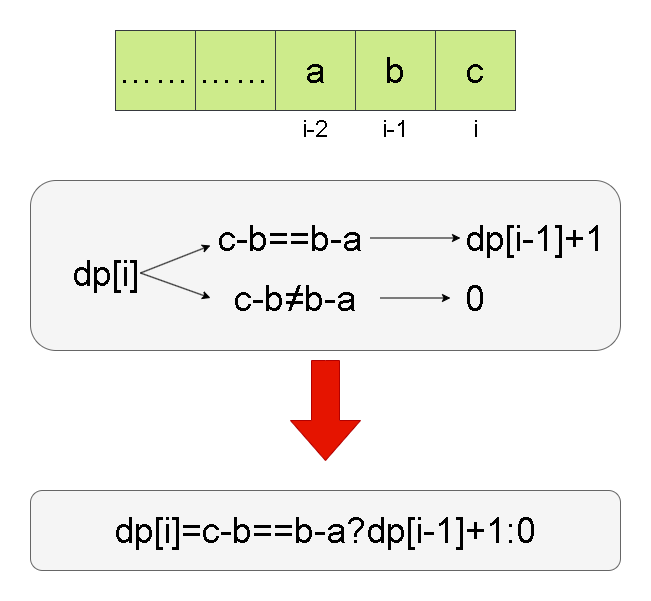
1. 题目链接:413. 等差数列划分 2. 题目描述: 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。 例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。 给你一个整数数组 …...

导出主机上所有docker 镜像并导入到其它主机
保存镜像列表到文件 docker images --format “{{.Repository}}:{{.Tag}}” > image_list.txt 导出列表中所有镜像到tar文件 cat image_list.txt | xargs -L 1 docker save -o all_images.tar 导入tar包中所有镜像 docker load -i all_images.tar...

HTML5+CSS3+JS小实例:焦点图波浪切换动画特效
实例:焦点图波浪切换动画特效 技术栈:HTML+CSS+JS 字体图标库:Font Awesome 效果: 源码: 【HTML】 <!DOCTYPE html> <html><head><meta http-equiv="content-type" content="text/html; charset=utf-8"><meta name=&…...
Mac电脑如何安装git
一、简介 在Mac上安装Git之前,可以先使用git --version来查看一下是否安装了Git,因为Mac系统可能自带了Git,或者在你安装XCode(或者XCode的命令行工具)时,可能已经安装了 Git。 如果Mac还没有安装Git的话&…...
macOS本地调试k8s源码
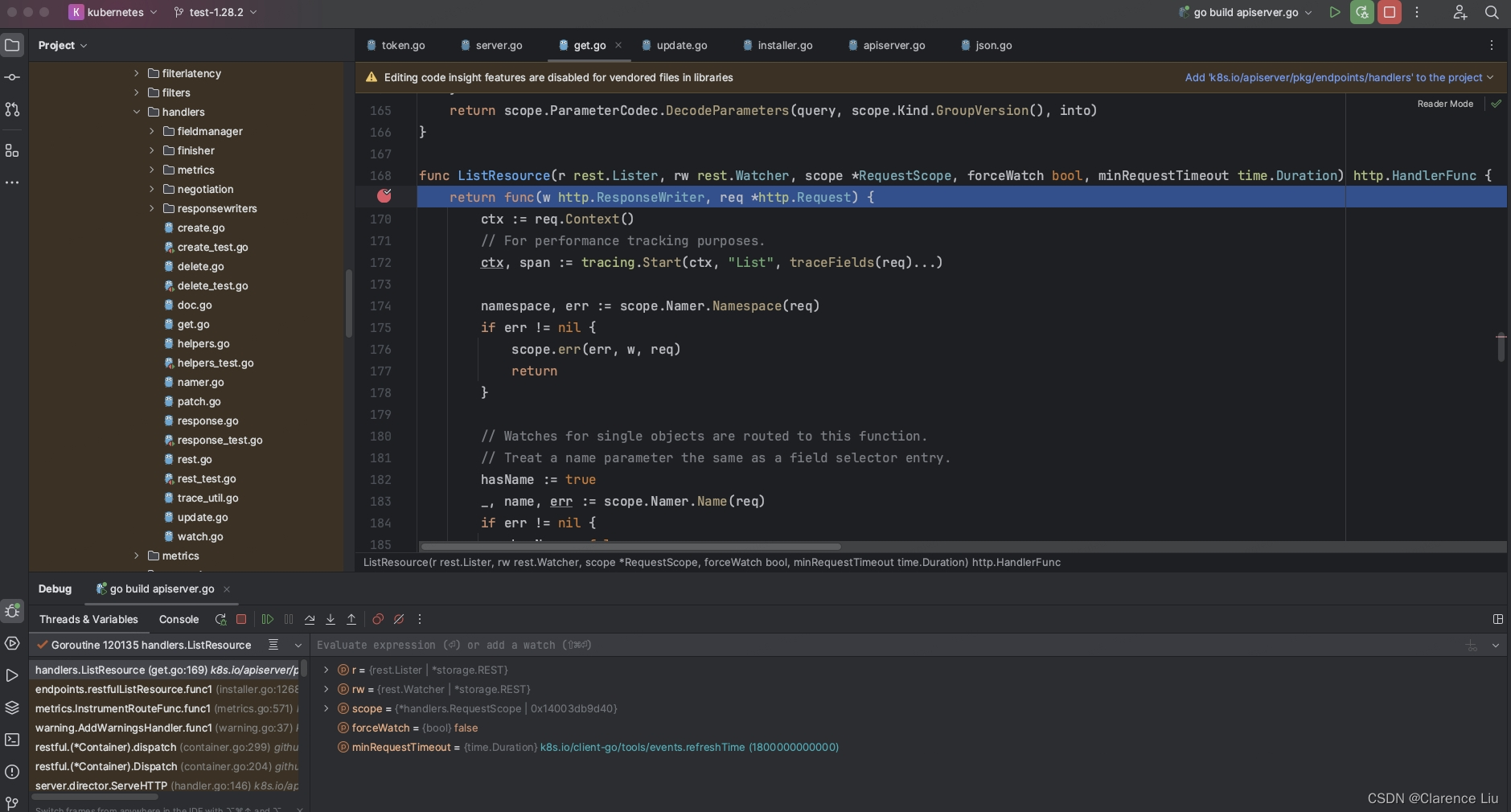
目录 准备工作创建集群注意点1. kubeconfig未正常加载2. container runtime is not running3. The connection to the server 172.16.190.132:6443 was refused - did you specify the right host or port?4. 集群重置5.加入子节点 代码调试 准备工作 apple m1芯片 安装vmwa…...

JS 实现一键复制文本内容
1、演示: 2、代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>一键复制</title&g…...

【Linux】echo命令使用
echo命令 功能是在显示器上显示一段文字,一般起到一个提示的作用。此外,也可以直接在文件中写入要写的内容。也可以用于脚本编程时显示某一个变量的值,或者直接输出指定的字符串。 著者 由布莱恩福克斯和切特拉米撰写。 语法 echo […...

Day03 嵌入式---中断
目录 一、简单介绍 二、总体框架 三、NVIC 3.2 NVIC的寄存器 3.3 中断向量表 3.4 中断优先级 3.5 NVIC优先级分组 3.6 NVIC配置 3.6.1、设置中断分组 3.6.2、初始化 四、EXTI 外部中断 4.1.EXTI的基本概念 4.2.EXTI的⼯作原理 4.3 EXTI配置 五、SYSCFG 5.1 SYS…...
wpf devexpress 使用IDataErrorInfo实现input验证
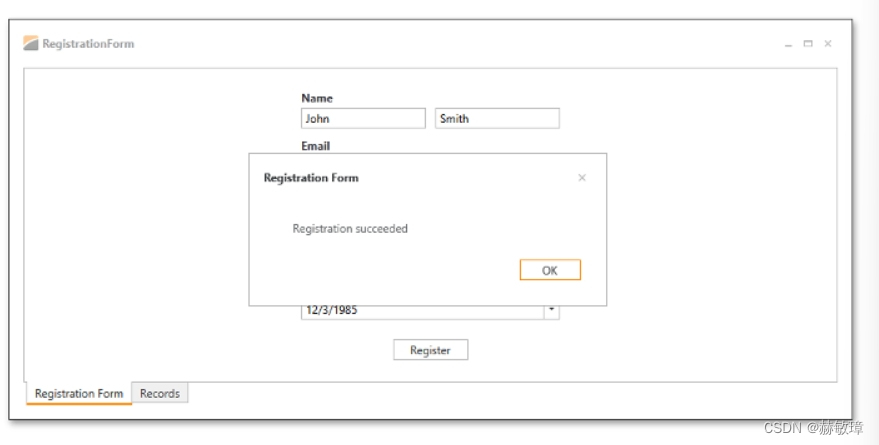
此处下载源码 当form初始化显示,Register按钮应该启动和没有输入错误应该显示。如果用户点击注册按钮在特定的输入无效数据,form将显示输入错误和禁用的注册按钮。实现逻辑在标准的IDataErrorInfo接口。请查阅IDataErrorInfo接口(System.Com…...

shell_81.Linux在命令行中创建使用函数
在命令行中使用函数 在命令行中创建函数 两种方法 单行方式来定义函数: $ function divem { echo $[ $1 / $2 ]; } $ divem 100 5 20 $ 当你在命令行中定义函数时,必须在每个命令后面加个分号,这样 shell 就能知道哪里是命令的起止了&am…...
)
鱼香ROS一键安装命令(支持微信、docker、ros等)
按照指定的数字选择即可。 wget http://fishros.com/install -O fishros && . fishros小鱼的一键安装系列 [14个ROS版本任你选]一键安装Docker使用指南...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
