整数和浮点数在内存中的存储(大小端详解)
目录
一、整数在内存中的存储
二、大小端字节序和字节序判断
2.1为什么有大小端?
2.2请简述大端字节序和小端字节序的概念,设计一个小程序来判断当前机器的字节序。(10分)-百度笔试题
方法一(char*强制类型转换):
方法二(联合体)
若想了解更多联合体的知识,请见拙作:
2.3unsign打印负数
2.4下列代码打印的结果
2.5下面代码的输出结果
三、浮点数在内存中的存储
3.1 浮点数存的过程
IEEE 754 对有效数字M和指数E,还有一些特别规定。
至于指数E,情况就比较复杂
3.2 浮点数取的过程
指数E从内存中取出还可以再分成三种情况:
E不全为0或不全为1
E全为0
E全为1
一、整数在内存中的存储
在讲解操作符的时候,我们就讲过了下面的内容:
整数的2进制表示方法有三种,即 原码、反码和补码
三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”,而数值位最
高位的一位是被当做符号位,剩余的都是数值位。
正整数的原、反、补码都相同。
负整数的三种表示方法各不相同。如图:

原码:直接将数值按照正负数的形式翻译成二进制得到的就是原码。
反码:将原码的符号位不变,其他位依次按位取反就可以得到反码。
补码:反码+1就得到补码。
对于整形来说:数据存放内存中其实存放的是补码
二、大小端字节序和字节序判断
大端(存储)模式:是指数据的低位字节内容保存在内存的高地址处,而数据的高位字节内容,保存在内存的低地址处。
小端(存储)模式:是指数据的低位字节内容保存在内存的低地址处,而数据的高位字节内容,保存在内存的高地址处。


根据此图判断此时机器为小端,因为44作为低字节内容(按顺序排在最后)应放在低地址处。
2.1为什么有大小端?
这是因为在计算机系统中,我们是以字节为单位的,每个地址单元都对应着一个字节,一个字节为8 bit 位,但是在C语言中除了8 bit 的 char 之外,还有16 bit (2个字节)的 short 型,32 bit (4个字节)的 long 型(要看具体的编译器),另外,对于位数大于8位的处理器,例如16位或者32位的处理器,由于寄存器宽度大于一个字节,那么必然存在着一个如何将多个字节安排的问题。因此就导致了大端存储模式和小端存储模式。
2.2请简述大端字节序和小端字节序的概念,设计一个小程序来判断当前机器的字节序。(10分)-百度笔试题
方法一(char*强制类型转换):
int check_sys()
{int i = 1;return (*(char*)&i);
}
int main()
{int ret = check_sys();if (ret == 1){printf("小端\n");}else{printf("大端\n");}return 0;
}-
int i = 1; 定义了一个整数 i 并赋值为1。在内存中,整数通常占用4个字节(这取决于系统,但在这里我们假设为4字节)。如果系统是小端的,这四个字节的存储形式将是 01 00 00 00。如果是大端的,存储形式将是 00 00 00 01
-
return ((char)&i); 这行代码做了以下操作:
1、&i: 获取 i 的地址。
2、(char*)&i: 将 i 的地址转换为 char 指针。由于 char 是1字节的,我们可以通过 char 指针来 访问整数的每一个字节。
3、(char)&i: 通过 char 指针解引用,获取整数的第一个字节。
-
如果系统是小端的,那么整数的第一个字节将是 1(或者 01 in hex)。如果是大端的,那么整数的第一个字节将是 0(或者 00 in hex)。
-
在 main() 函数中,根据 ret 的值(即整数的第一个字节)判断系统是大端还是小端,并打印相应的结果。
方法二(联合体)
若想了解更多联合体的知识,请见拙作:

返回1是小端,返回0是大端
如果系统是小端的,那么在内存中存储这个整数的最低字节(也就是字节 c)将会是1,因为最低字节存储在最低的内存地址处。而如果系统是大端的,那么最低有效字节将会是0。
int check_sys()
{union{int i;char c;}un;un.i = 1;return un.c;
}int main()
{int ret = check_sys();if (ret == 1){printf("小端\n");}else {printf("大端\n");}return 0;
}2.3unsign打印负数
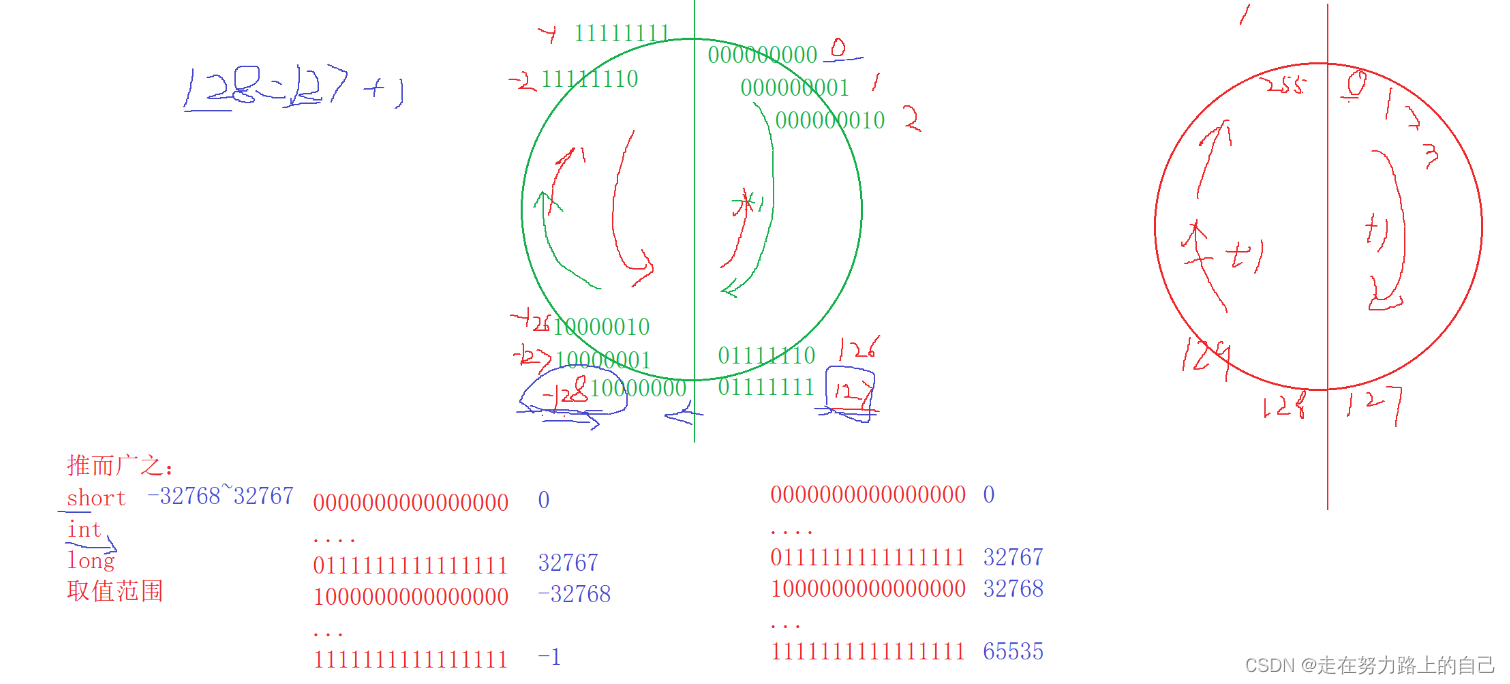
int main()
{char a = -128;//10000000000000000000000010000000//11111111111111111111111101111111//11111111111111111111111110000000//10000000 - a//打印时发生整型提升//11111111111111111111111110000000//sign char 的取值范围:-128~127//unsigned char的取值范围:0~255printf("%u\n", a);//4,294,967,168//%u是十进制的形式打印无符号的整数return 0;
}char类型存储的顺序如下:

2.4下列代码打印的结果
int main()
{char a[1000];int i;for (i = 0; i < 1000; i++){a[i] = -1 - i;}printf("%d", strlen(a));//255return 0;
}
-
char的范围:-128~127
-
a[1]~a[1000]的值规律如下:
-1 -2 -3 ...... -128 127 126 125 ...... 5 4 3 2 1 0 -1 -2 ...... -128 127 126 ......5 4 3 2 1……
-
strlen求字符串长度找的是\0,\0的ASCII码值是0,其实找的就是0,所以到0就终止
-
所以strlen计算的长度为:128+127 = 255
2.5下面代码的输出结果
int main()
{int a[4] = { 1, 2, 3, 4 };//小端环境int* ptr1 = (int*)(&a + 1);int* ptr2 = (int*)((int)a + 1);printf("%x" ,ptr1[-1]);printf("%x", *ptr2);return 0;
}ptr1[-1]--> *(ptr1 - 1)-->*((&a+1) - 1)-->4

三、浮点数在内存中的存储

举例来说:
十进制的5.0,写成二进制是 101.0 ,相当于 1.01×2^2 。
那么,按照上面V的格式,可以得出S=0,M=1.01,E=2。
十进制的-5.0,写成二进制是 -101.0 ,相当于 -1.01×2^2 。那么,S=1,M=1.01,E=2。
IEEE 754规定:
对于32位的浮点数,最高的1位存储符号位S,接着的8位存储指数E,剩下的23位存储有效数字M
int main()
{int n = 9;float* pFloat = (float*)&n;//int*printf("n的值为:%d\n", n);//9printf("*pFloat的值为:%f\n", *pFloat);//0.000000*pFloat = 9.0;printf("num的值为:%d\n", n);//1091567616printf("*pFloat的值为:%f\n", *pFloat);//9.000000return 0;
}-
创建了一个浮点数指针 pFloat 并将其指向 n 的内存地址。此时,pFloat 指向的内存中存储的是一个整数值 9。
-
通过 pFloat 打印该值时,由于 pFloat 是一个浮点数指针,所以它会尝试将内存中的值解释为浮点数。在大多数系统上,整数 9 和浮点数 9.0 在内存中的表示是不同的。

-
接下来,你通过 pFloat 将该内存位置的值设置为 9.0。这意味着你现在改变了原来存储整数 9 的内存,使其现在包含一个浮点数的表示。
-
再次尝试打印整数 n 的值时,它会尝试将内存中的浮点数表示解释为一个整数。这就是为什么你得到了一个奇怪的数字 1091567616(这个数字是 9.0 的 IEEE 754 单精度表示形式解释为整数时的结果)。

-
而当打印 *pFloat 的值时,它正确地显示为 9.0。

3.1 浮点数存的过程
但是因为存储有可能会改变原先的值。
10: 5.5
2: 101.1
科学计数法:1.011 * 2^2
(-1)^0 *1.011 *2^2
S = 0
E = 2
M = 1.011
int main()
{float f = 99.7f;printf("%f\n", f);////0 10000001 01100000000000000000000//0x40 B0 00 00//1.01100000000000000000000 *2^2return 0;
}IEEE 754 对有效数字M和指数E,还有一些特别规定。
前面说过, 1≤M<2 ,也就是说,M可以写成 1.xxxxxx 的形式,其中 xxxxxx 表示小数部分。
IEEE 754 规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分。比如保存1.01的时候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。以32位浮点数为例,留给M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字。
至于指数E,情况就比较复杂
首先,E为一个无符号整数(unsigned int)
这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的取值范围为0~2047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE 754规定,存入内存时E的真实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。比如,2^10的E是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
3.2 浮点数取的过程
指数E从内存中取出还可以再分成三种情况:
E不全为0或不全为1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将有效数字M前加上第一位的1。
比如:0.5 的二进制形式为0.1,由于规定正数部分必须为1,即将小数点右移1位,则为1.0*2^(-1),其
阶码为-1+127(中间值)=126,表示为01111110,而尾数1.0去掉整数部分为0,补齐0到23位
00000000000000000000000,则其二进制表示形式为:
1 0 01111110 00000000000000000000000
(以下两种了解便可)
E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值,有效数字M不再加上第一位的1,而是还
原为0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字。
1 0 00000000 00100000000000000000000
E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);
1 0 11111111 00010000000000000000000
好了,关于浮点数的表示规则,就说到这里。
今天就先到这里了!!!

看到这里了还不给博主扣个:
⛳️ 点赞☀️收藏 ⭐️ 关注!
你们的点赞就是博主更新最大的动力!
有问题可以评论或者私信呢秒回哦。
相关文章:

整数和浮点数在内存中的存储(大小端详解)
目录 一、整数在内存中的存储 二、大小端字节序和字节序判断 2.1为什么有大小端? 2.2请简述大端字节序和小端字节序的概念,设计一个小程序来判断当前机器的字节序。(10分)-百度笔试题 方法一(char*强制类型转换)…...
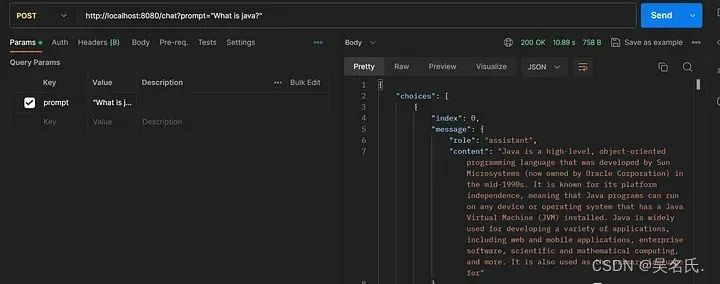
SpringBoot 集成 ChatGPT,实战附源码
1 前言 在本文中,我们将探索在 Spring Boot 应用程序中调用 OpenAI ChatGPT API 的过程。我们的目标是开发一个 Spring Boot 应用程序,能够利用 OpenAI ChatGPT API 生成对给定提示的响应。 您可能熟悉 ChatGPT 中的术语“提示”。在 ChatGPT 或类似语…...

数据结构——希尔排序(详解)
呀哈喽,我是结衣 不知不觉,我们的数据结构之路已经来到了,排序这个新的领域,虽然你会说我们还学过冒泡排序。但是冒泡排序的性能不高,今天我们要学习的希尔排序可就比冒泡快的多了。 希尔排序 希尔排序的前身是插入排…...
C++ day53 最长公共子序列 不相交的线 最大子序和
题目1:1143 最长公共子序列 题目链接:最长公共子序列 对题目的理解 返回两个字符串的最长公共子序列的长度,如果不存在公共子序列,返回0,注意返回的是最长公共子序列,与前一天的最后一道题不同的是子序…...

ubuntu中删除镜像和容器、ubuntu20.04配置静态ip
1 删除镜像 # 短id sudo docker rmi 镜像id # 完整id sudo docker rmi 镜像id# 镜像名【REPOSITORY:TAG】 sudo docker rmi redis:latest2 删除容器 # 删除某个具体容器 sudo docker rm 容器id# 删除Exited状态/未运行的容器,三种命令均可 sudo docker rm docker …...

华为手环 8 五款免费表盘已上线,请注意查收
华为手环 8,作为一款集时尚与实用于一体的智能手环,不仅具备强大的功能,还经常更新的表盘样式,让用户掌控时间与健康的同时,也能展现自己的时尚品味。这不,12 月官方免费表盘又上新了,推出了五款…...

JOSEF约瑟 同步检查继电器DT-13/200 100V柜内安装,板前接线
系列型号 DT-13/200同步检查继电器; DT-13/160同步检查继电器; DT-13/130同步检查继电器; DT-13/120同步检查继电器; DT-13/90同步检查继电器; DT-13/254同步检查继电器; 同步检查继电器DT-13/200 100V柜内板前接线 一、用途 DT-13型同步检查继电器用于两端供电线路的…...

龙迅#LT8311X3 USB中继器应用描述!
1. 概述 LT8311X3是一款USB 2.0高速信号中继器,用于补偿ISI引起的高速信号衰减。通过外部下拉电阻器选择的编程补偿增益有助于提高 USB 2.0 高速信号质量并通过 CTS 测试。 2. 特点 • 兼容 USB 2.0、OTG 2.0 和 BC 1.2• 支持 HS、FS、LS 信令 • 自动检测和补偿 U…...

eclipse jee中 如何建立动态网页及服务的设置问题
第一次打开eclipse 时,设置工作区时,一定是空目录 进入后 File-----NEW------Dynamic Web Project 填 项目名,不要有大写 m1 next next Generate前面打对勾 finish 第一大步: window----Preferences type filter text 处填 :Serve…...
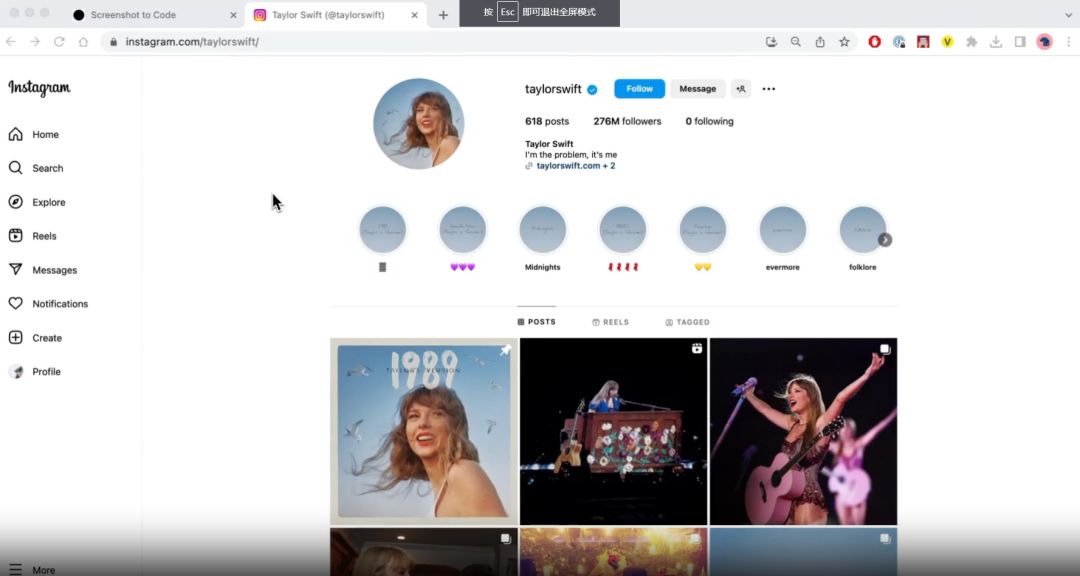
一张网页截图,AI帮你写前端代码,前端窃喜,终于不用干体力活了
简介 众所周知,作为一个前端开发来说,尤其是比较偏营销和页面频繁改版的项目,大部分的时间都在”套模板“,根本没有精力学习前端技术,那么这个项目可谓是让前端的小伙伴们看到了一丝丝的曙光。将屏幕截图转换为代码&a…...

处理k8s中创建ingress失败
创建ingress: 如果在创建过程中出错了: 处理方法就是: kubectl get ValidatingWebhookConfiguration kubectl delete -A ValidatingWebhookConfiguration ingress-nginx-admission 然后再次创建,发现可以:...
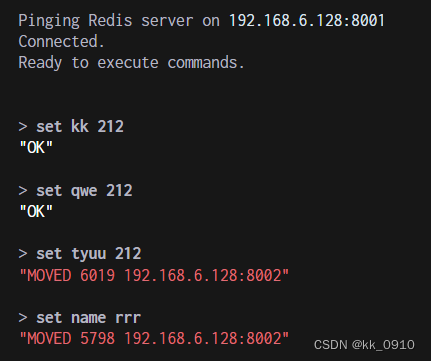
Redis高可用集群架构
高可用集群架构 哨兵模式缺点 主从切换阶段, redis服务不可用,高可用不太友好只有单个主节点对外服务,不能支持高并发单节点如果设置内存过大,导致持久化文件很大,影响数据恢复,主从同步性能 高可用集群…...

JAVA常见问题解答:解决Java 11新特性兼容性问题的六个步骤
引言: 随着技术的不断发展,Java作为一种被广泛使用的编程语言,也在不断更新和改进。Java 11作为Java的最新版本,带来了许多新的特性和改进。然而,对于一些老旧的Java应用程序来说,升级到Java 11可能会带来一…...
【C语言】深入理解指针(1)
目录 前言 (一)内存与地址 从实际生活出发 地址 内存 内存与地址关系密切 (二)指针变量 指针变量与取地址操作符 指针变量与解引用操作符 指针的大小 指针的运算 指针 - 整数 指针-指针 指针的关系运算 指针的类型的…...
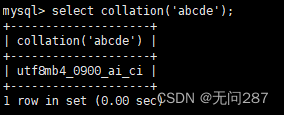
MySQL的系统信息函数
系统信息函数让你更好的使用MySQL数据库 1、version()函数 查看MySQL系统版本信息号 select version();2、connection_id()函数 查看当前登入用户的连接次数 直接调用CONNECTION_ID()函数--不需任何参数--就可以看到当下连接MySQL服务器的连接次数,不同时间段该…...
 方法)
python中.format() 方法
.format() 方法是一种用于格式化字符串的方法,它允许将变量的值插入到字符串中的占位符位置上。该方法可以接受一个或多个参数,并根据给定的格式规则将它们插入到字符串中。 下面是一些使用 .format() 方法的示例: # 基本用法 name "…...
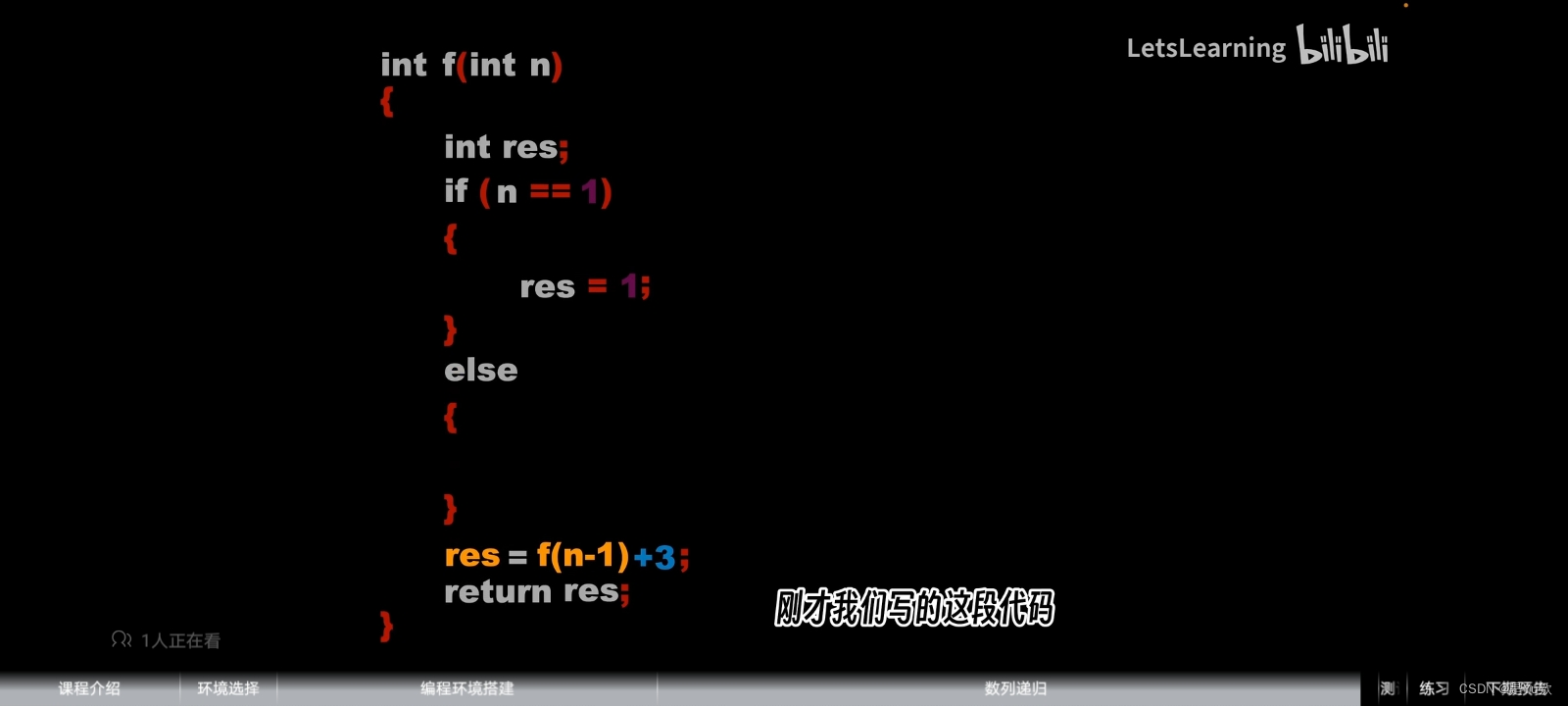
【新手解答8】深入探索 C 语言:递归与循环的应用
C语言的相关问题解答 写在最前面问题:探索递归与循环在C语言中的应用解析现有代码分析整合循环示例代码修改注意事项结论 延伸:递归和循环的退出条件设置解析使用递归使用循环选择适合的方法 写在最前面 一位粉丝私信交流,回想起了当初的我C…...
服务器中深度学习环境的配置
安装流程 11.17 日,周末去高校参加学术会议,起因, 由于使用了某高校内的公共有线网络, 远程连接服务器后,黑客利用 ssh 开放的 22 端口, 篡改了主机的配置, 使得只要一连上网络, 服…...

html实现各种好看的鼠标滑过图片特效模板
文章目录 1.鼠标悬浮效果1.1 渐动效果1.2 渐变效果1.3 边框效果1.4 线行效果1.5 图标效果1.6 块状效果1.7 边线效果1.8 放大效果1.9 渐出效果1.10 痕迹效果1.11 交叉效果1.12 着重效果1.13 详展效果1.14 能动效果1.15 明细效果 2.主要源码2.1 源代码 源码下载 作者:…...
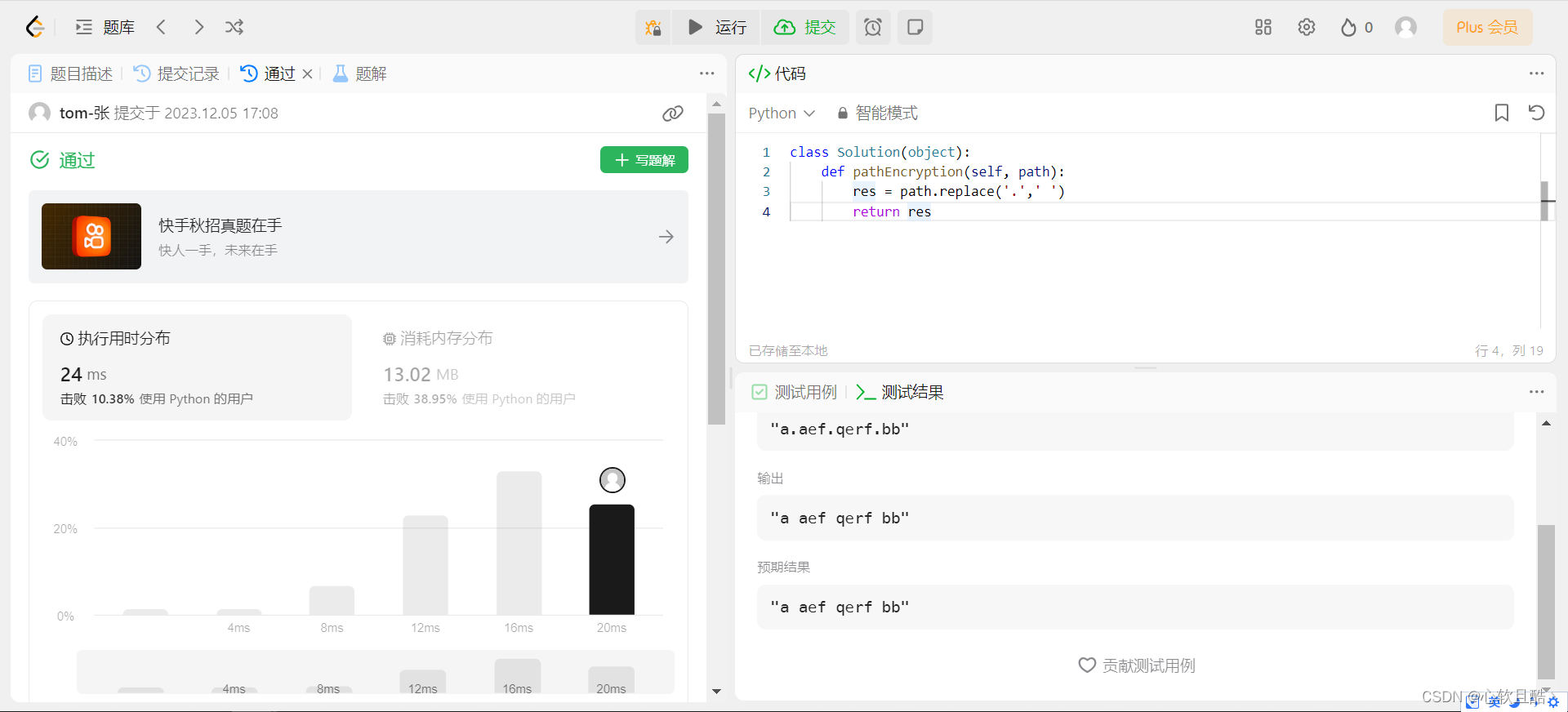
leetcode:LCR 122. 路径加密python3解法)
难度:简单 假定一段路径记作字符串 path,其中以 "." 作为分隔符。现需将路径加密,加密方法为将 path 中的分隔符替换为空格 " ",请返回加密后的字符串。 示例 1: 输入:path "a.a…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
