算法通关村第十八关-青铜挑战回溯是怎么回事
大家好我是苏麟 , 今天聊聊回溯是怎么个事 .
回溯是最重要的算法思想之一,主要解决一些暴力枚举也搞不定的问题,例如组合、分割、子集、排列,棋盘等。从性能角度来看回溯算法的效率并不高,但对于这些暴力都搞不定的算法能出结果就很好了,效率低点没关系
我们利用LeetCode 77 组合题来了解回溯 . 77.组合

大纲
- 从N叉树开始
- 为什么有的问题暴力搜索也不行
- 回溯 = 枚举 + 递归 + 撤销
回溯可以视为递归的拓展,很多思想和解法都与递归密切相关,在很多材料中都将回溯都与递归同时解释。因此学习回溯时,我们对比递归来分析其特征会理解更深刻。
- 递归策略: 先与意中人制造偶遇,然后了解人家的情况,然后约人家吃饭,有好感之后尝试拉人家的手,没有拒绝就表白。
- 回溯策略: 先统计周围所有的单身女孩,然后一个一个表白,被拒绝就说“我喝醉了”,然后就当啥也没发生,继续找下一个
回溯最大的好处是有非常明确的模板,所有的回溯都是一个大框架,因此透彻理解回溯的框架是解决一切回溯问题的基础
回溯不是万能的,而且能解决的问题也是非常明确的,例如组合、分割、子集、排列,棋盘等等,不过这些问题具体处理时又有很多不同
回溯模板 :
void huisu(参数){if(){return;}for(){处理......huisu();......}
}
从N叉树开始
在解释回溯之前,我们先看一下N叉树遍历的问题,我们知道在二又树中,按照前序遍历的过程如下所示 :
public class TreeNode {int val;TreeNode left;TreeNode right;}public void nodeVal(TreeNode node){if(node == null){return;}System.out.println(node.val);nodeVal(node.left,list);nodeVal(node.right,list);}
}
假如我现在是一个三叉、四叉甚至N叉树该怎么办呢? 很显然这时候就不能用 left 和 right 来表示分支了,使用一个List比较好,也就是这样子 :
N 叉树的定义 :
class TreeNode{int val;List<TreeNode> nodes;
}
遍历的代码 :
public void nodeVal(TreeNode node){if(node == null){return;}System.out.println(node.val);for(int i = 1;i <= nodes.length;i++){nodeVal(第i个节点);}}
}
到这里,你有没有发现和上面说的回溯的模板非常像了? 是的!非常像!既然很像,那说明两者一定存在某种关系。其他暂时不管,现在你只要先明白回溯的大框架就是遍历N又树就行了。
为什么有的问题暴力搜索也不行
我们说回湖主要解决暴力枚举也解决不了的问题,什么问题这么神奇,暴力都搞不定?
LeetCode77: 给定两个整数 n 和 k,返回1…n 中所有可能的 k 个数的组合。
例如,输入n=4k=2,则输出 : [[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
首先明确这个题是什么意思,如果n=4,k=2,那就是从4个数中选择2个,问你最后能选出多少组数据。这个是高中数学中的一个内容,过程大致这样: 如果n=4,那就是所有的数字为{1,2,3,4)
- 1.先取一个1,则有[1,2],[1,3],[1,4]三种可能
- 2.然后取一个因为1已经取过了,不再取,则有[2,3],[2,4]两种可能
- 3.再取一个3,因为1和2都取过了,不再取,则有[3,4]一种可能
- 4.再取4,因为1,2,3都已经取过了,所以直接返回null
- 5.所以最终结果就是[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]
这就是我们思考该问题的基本过程,写成代码也很容易,双层循环轻松搞定
int n = 4; for (int i = 1; i <= n; i++) { for (int j = i + 1; j <= n; j++) { System.out.println(i + " " + j); }
}
假如n和k都变大,比如n是200,k是3呢? 也可以,三层循环基本搞定
int n = 200;
for (int i = 1; i <= n; i++) { for (int j = i + 1; j <= n; j++) { for (int u = j + 1; u <= n; n++) { System.out.println(i + " " + j + " " + u); } }
}
如何这里的K是5呢? 甚至是50呢? 你需要套多少层循环? 甚至告你K就是一个末知的正整数k,你怎么写循环呢?这时候已经无能为例了? 所以暴力搜索就不行了。
这就是组合类型问题,除此之外子集、排列、切割、棋盘等方面都有类似的问题,因此我们要找更好的方式。
回溯 = 枚举 + 递归 + 撤销
我们继续研究LeetCode77题,我们图示一下上面自己枚举所有答案的过程。
n=4时,我们可以选择的n有 1,2,3,4这四种情况,所以我们从第一层到第二层的分支有四个,分别表示可以取1,2,3,4。而且这里 从左向右取数,取过的数,不在重复取。第一次取1,集合变为2,3,4,因为k为2,我们只需要再取一个数就可以了,分别取2,3,4,得到集合[1,2] [1,3][1,4],以此类推横向:
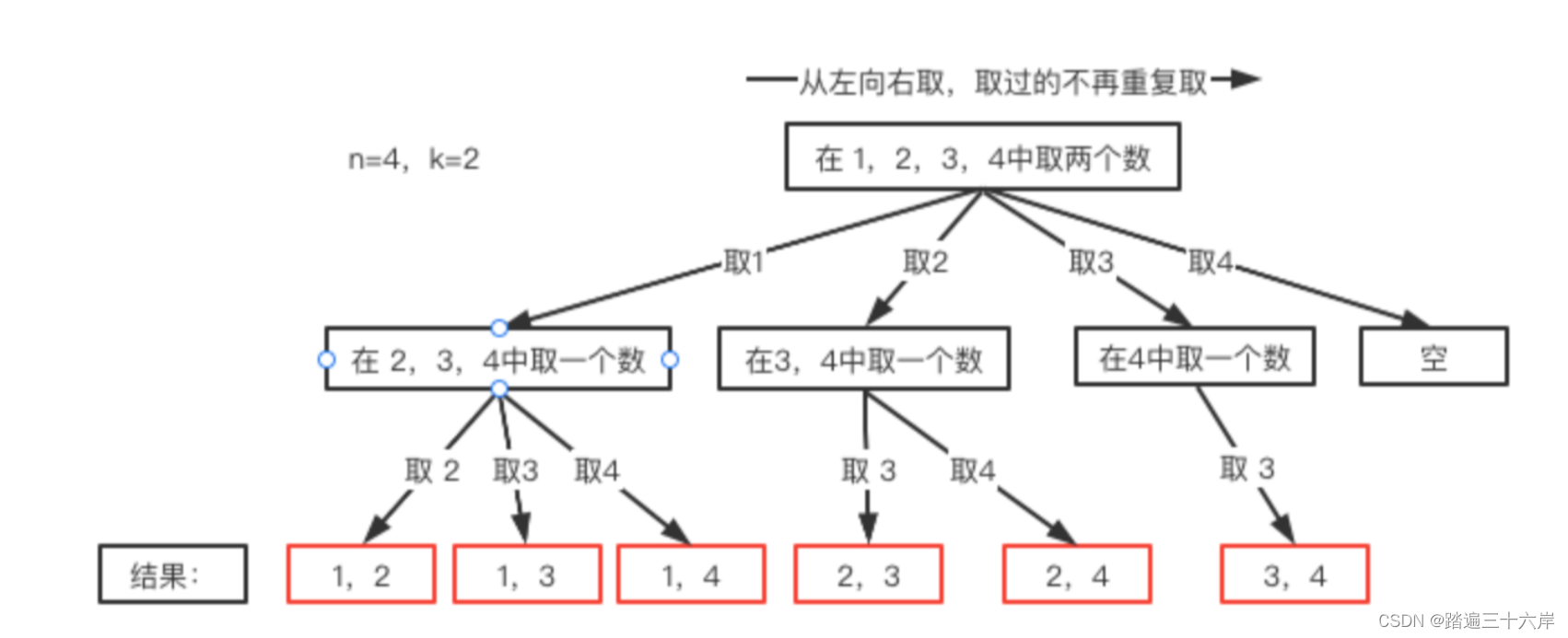
每次从集合中选取元素,可选择的范围会逐步收缩,到了取4时就直接为空了
继续观察树结构,可以发现,图中每次访问到一次叶子节点(图中红框标记处),我们就找到了一个结果。虽然最后一个是空,但是不影响结果。这相当于只需要把从根节点开始每次选择的内容(分支)达到叶子节点时,将其收集起来就是想要的结果。
如果感觉不明显,我们再画一个n=5,k=3的例子:
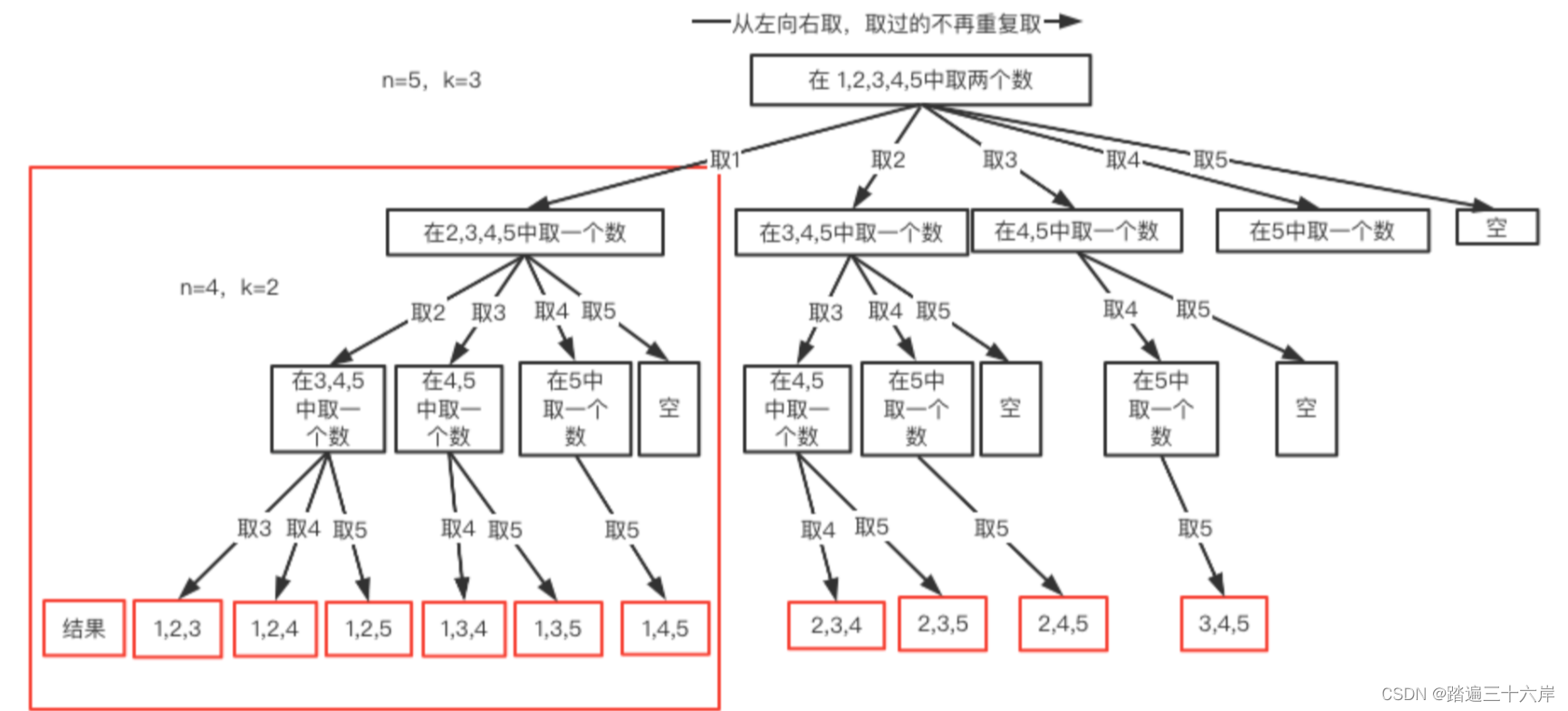
从图中我们发现元素个数n相当于树的宽度(横向),而每个结果的元素个数k相当于树的深度(纵向)。所以我们说回溯算法就是一纵一横而已。再分析,我们还发现几个规律:
- 我们每次选择都是从类似{1,2,3,4),1,2,3,4,5这样的序列中一个个选的,这就是局部枚举,而且越往后枚举范围越小。
- 枚举时,我们就是简单的暴力测试而已,一个个验证,能否满足要求,从上图可以看到,这就是N叉树遍历的过程,因此两者代码也必然很像。
- 我们再看上图中红色大框起来的部分,这个部分的执行过程与n=4,k=2的处理过程完全一致,很明显这是个可以递归的子结构。
这样我们就将回溯与N叉树的完美结合在一起了
到此,还有一个大问题没有解决,回溯一般会有个手动撤销的操作,为什么要这样呢? 继续观察纵横图:
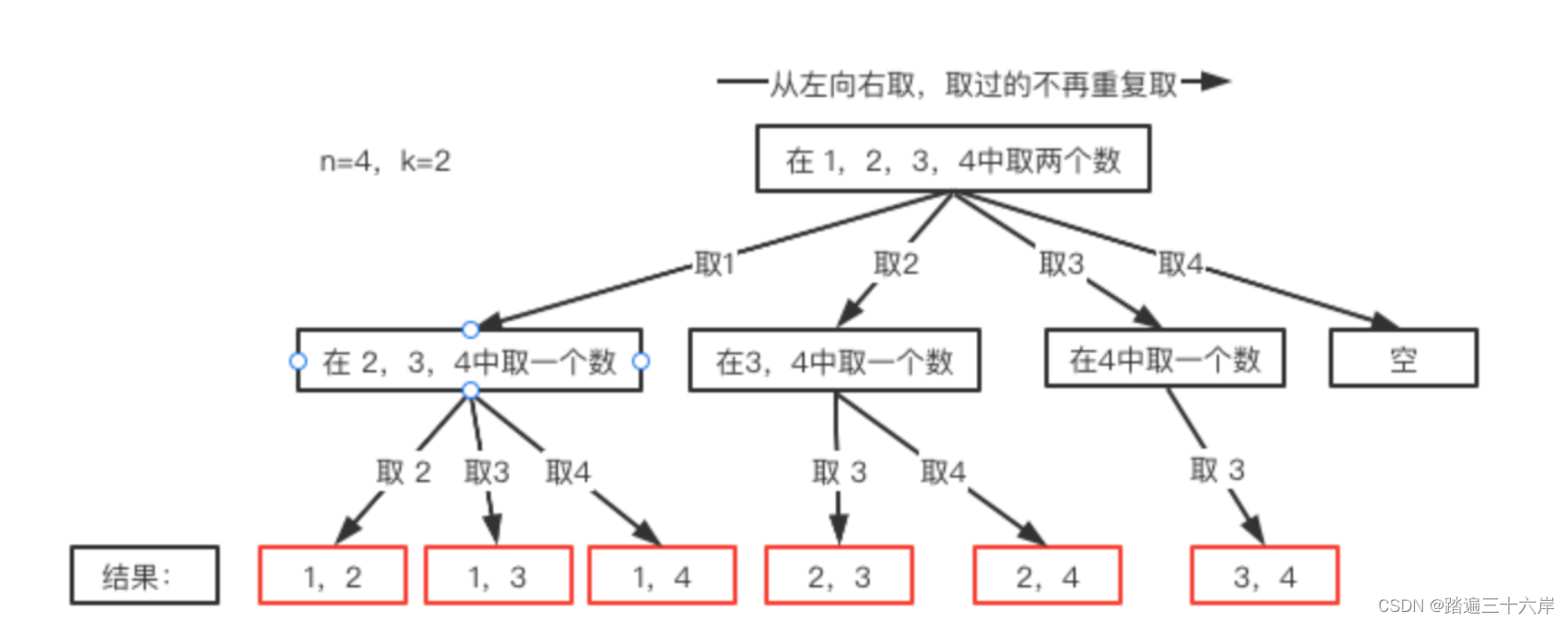
我们可以看到,我们收集每个结果不是针对叶子结点的,而是针对树枝的,比如最上层我们首先选了1,下层如果选2,结果就是(1,2),如果下层选了3,结果就是(1,3),依次类推。现在的问题是当我们得到第一个结果{1,2)之后,怎么得到第二个结果(1,3}呢?
继续观察纵横图,可以看到,我可以在得到(1,2)之后将2撤掉,再继续取3,这样就得到了(1,3},同理可以得到{1,4},之后当前层就没有了,我们可以将1撤销,继续从最上层取2继续进行。
这里对应的代码操作就是先将第一个结果放在临时列表 deque 里,得到第一个结果(1,2)之后就将path里的内容放进结果列表 list 中,之后,将 deque 里的2撤销掉,继续寻找下一个结果{1.3},然后继续将 deque 放入list,然后再撤销继续找。
这几条就是回溯的基本规律,明白之后,一切都变得豁然开朗。
到此我们就可以写出完整的回溯代码了 :
class Solution {public List<List<Integer>> combine(int n, int k) {List<List<Integer>> list = new ArrayList<>();if(n <= 0 || n < k){return list;}Deque<Integer> deque = new ArrayDeque<>();dfs(n,k,1,list,deque);return list;}//dfs 深度优先搜索的意思public void dfs (int n,int k,int start,List<List<Integer>> list,Deque<Integer> deque){if(deque.size() == k){list.add(new ArrayList<>(deque));return;}for(int i = start;i <= n;i++){deque.addLast(i);dfs(n,k,i + 1,list,deque);deque.removeLast();}}
}
上面代码还有个问题要解释一下: start 和 i 是怎么变化的,为什么传给下一层时要加 1.我们可以看到在递归里有个循环
for (int i = startIndex; i <= n; i++) { dfs(n,k,i+1,path,res);
}
这里的循环有什么作用呢? 看一下图就知道了,这里其实就是枚举,第一次n=4,可以选择1,2,3,4四种情况,所以就有四个分支,for循环就会执行四次:
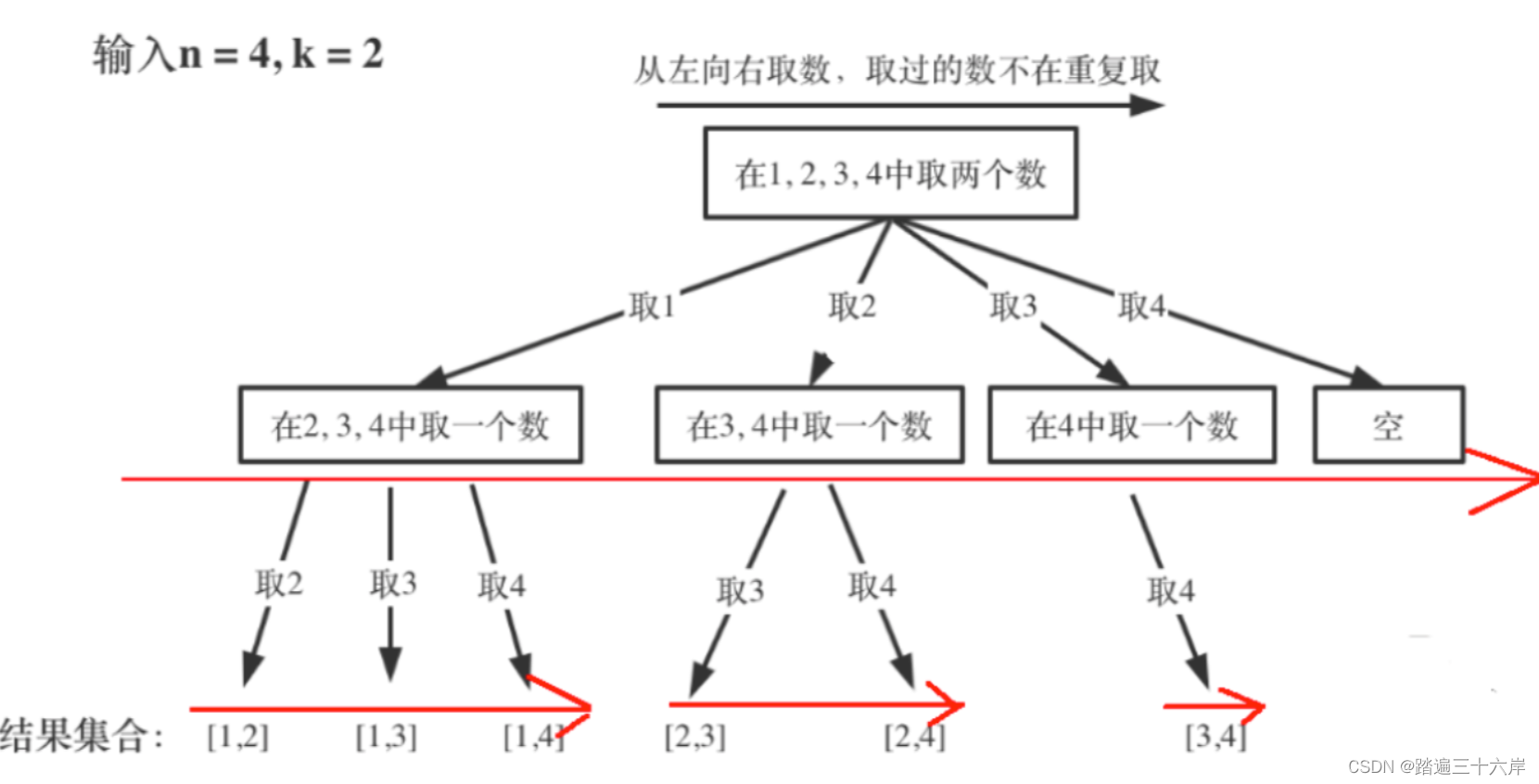
而对于第二层第一个,选择了1之后,剩下的元素只有2,3,4了,所以这时候for循环就执行3次,后面的则只有2次和1次。
这期就到这里 , 下期见!
相关文章:

算法通关村第十八关-青铜挑战回溯是怎么回事
大家好我是苏麟 , 今天聊聊回溯是怎么个事 . 回溯是最重要的算法思想之一,主要解决一些暴力枚举也搞不定的问题,例如组合、分割、子集、排列,棋盘等。从性能角度来看回溯算法的效率并不高,但对于这些暴力都搞不定的算法能出结果就…...
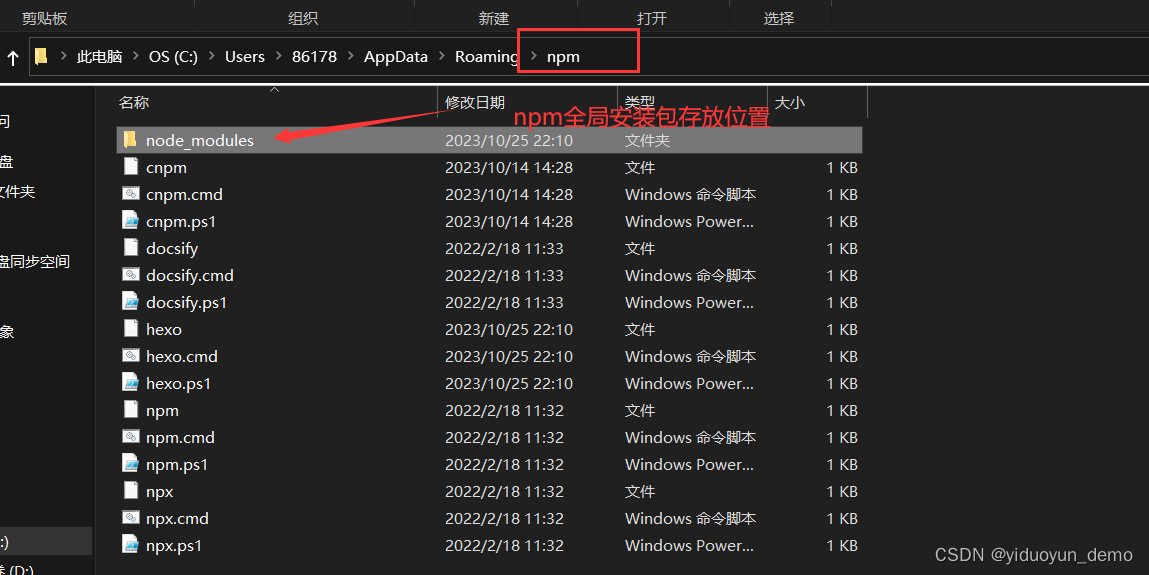
区分node,npm,nvm
目录 一,nodejs二,npm三,nvm 区分node,npm,nvm 几年前学习前端的时候学习的就是htmlcssjs 三件套。 现在只学习这些已经不能满足需要了。 一,nodejs nodejs是编程语言javascript运行时环境。(比…...

7-2 小霸王
幼儿园的老师给几位小朋友等量的长方体橡皮泥,但有个小朋友(小霸王)觉得自己的橡皮泥少了,就从另一个小朋友那里抢了一些。请问,是哪个小霸王抢了哪个小朋友的橡皮泥? 输入格式: 测试数据有多组。对于每组…...

Linux内核上游提交完整流程及示例
参考博客文章: 向linux内核提交代码 - 知乎 一、下载Linux内核源码 通过git下载Linux内核源码,具体命令如下: git clone git://git.kernel.org/pub/scm/linux/kernel/git/torvalds/linux.git 实际命令及结果如下: penghaoDin…...

TS学习——快速入门
TypeScript简介 TypeScript是JavaScript的超集。它对JS进行了扩展,向JS中引入了类型的概念,并添加了许多新的特性。TS代码需要通过编译器编译为JS,然后再交由JS解析器执行。TS完全兼容JS,换言之,任何的JS代码都可以直…...

深圳锐科达风力发电广播对讲解决方案
深圳锐科达风力发电广播对讲解决方案 风力发电对讲通常是在风塔的底部与机舱室安装一键对讲终端,可以一键呼叫控制中心值班人员,结构简单,组网方便,设备可以接入局域网或广域网构成功能应急呼叫系统。 系统实现的功能࿱…...

极智芯 | 解读国产AI算力 璧仞产品矩阵
欢迎关注我,获取我的更多经验分享 大家好,我是极智视界,本文分享一下 解读国产AI算力 璧仞产品矩阵。 璧仞在国产 AI 芯领域就是 "迷" 一样的存在,你要说它在市场上的 "建树" 泛善可陈的话,它又 "赫然" 在美国芯片禁令名单中。而这一切的一…...

Echarts折线图常见问题及案例代码
前言 ECharts 是一个使用 JavaScript 实现的开源可视化库,它可以帮助用户以简单的方式创建复杂的时间序列、条形图、饼图、地图等图形。 初学者,可参考下我的另外两篇文章,从基础到深入,解读饼状图的运用。 ECharts初始案例(入门) ECharts之折线图 常见问题及案例代码 …...
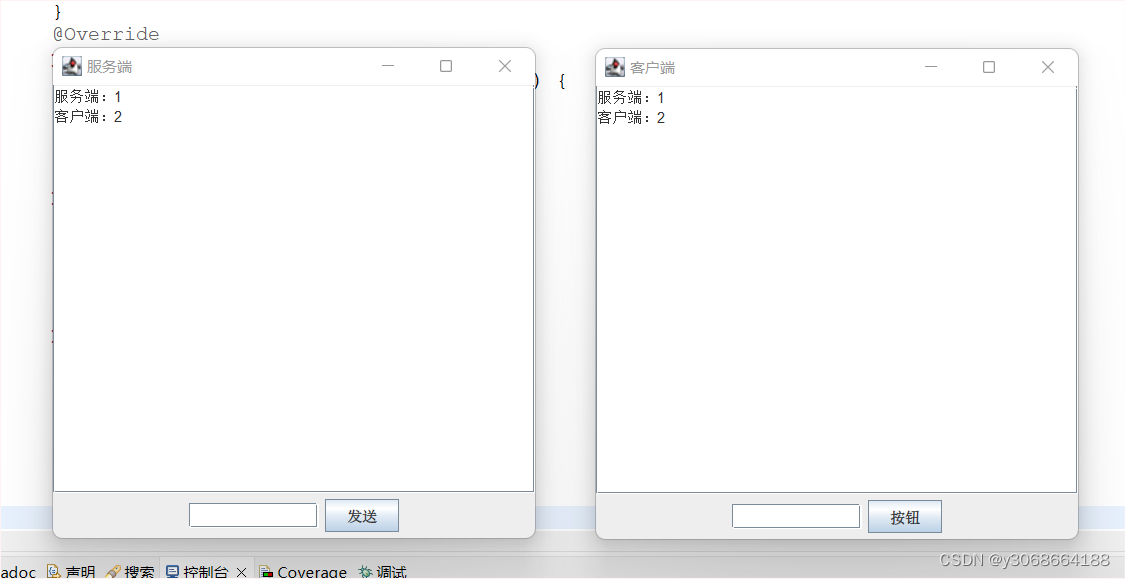
javaTCP协议实现一对一聊天
我们首先要完成服务端,不然出错,运行也要先运行服务端,如果不先连接服务端,就不监听,那客户端不知道连接谁 服务端 package d21z; import java.awt.BorderLayout; import java.awt.event.ActionEvent; import java.a…...
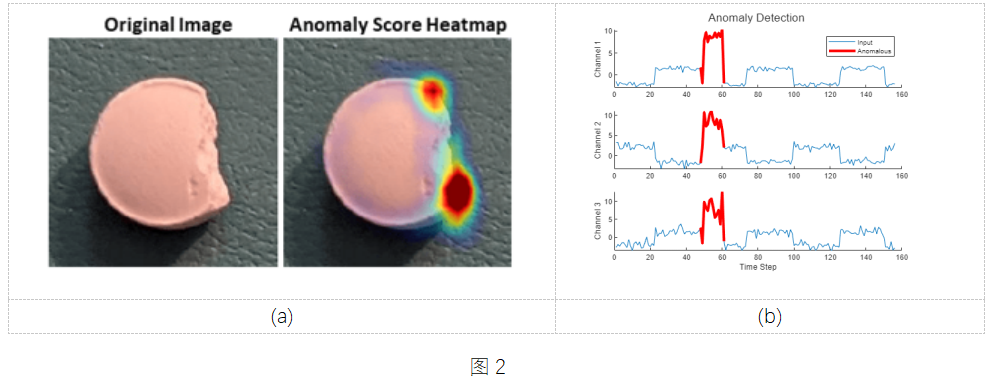
机器学习应用 | 使用 MATLAB 进行异常检测(上)
异常检测任务,指的是检测偏离期望行为的事件或模式,可以是简单地检测数值型数据中,是否存在远超出正常取值范围的离群值,也可以是借助相对复杂的机器学习算法识别数据中隐藏的异常模式。 在不同行业中,异常检测的典型…...

Java -jar参数详解
java -jar 命令用于执行打包成可执行 JAR 文件的 Java 应用程序。在运行时,你可以通过命令行传递参数给这个应用程序。 1. -jar 参数: 说明: 指定要执行的 JAR 文件。示例:java -jar your-application.jar 2. -D 参数ÿ…...
RocksDB 在 vivo 消息推送系统中的实践
作者:vivo 互联网服务器团队 - Zeng Luobin 本文主要介绍了 RocksDB 的基础原理,并阐述了 RocksDB 在vivo消息推送系统中的一些实践,通过分享一些对 RocksDB 原生能力的探索,希望可以给使用RocksDB的读者带来启发。 一、背景 在…...
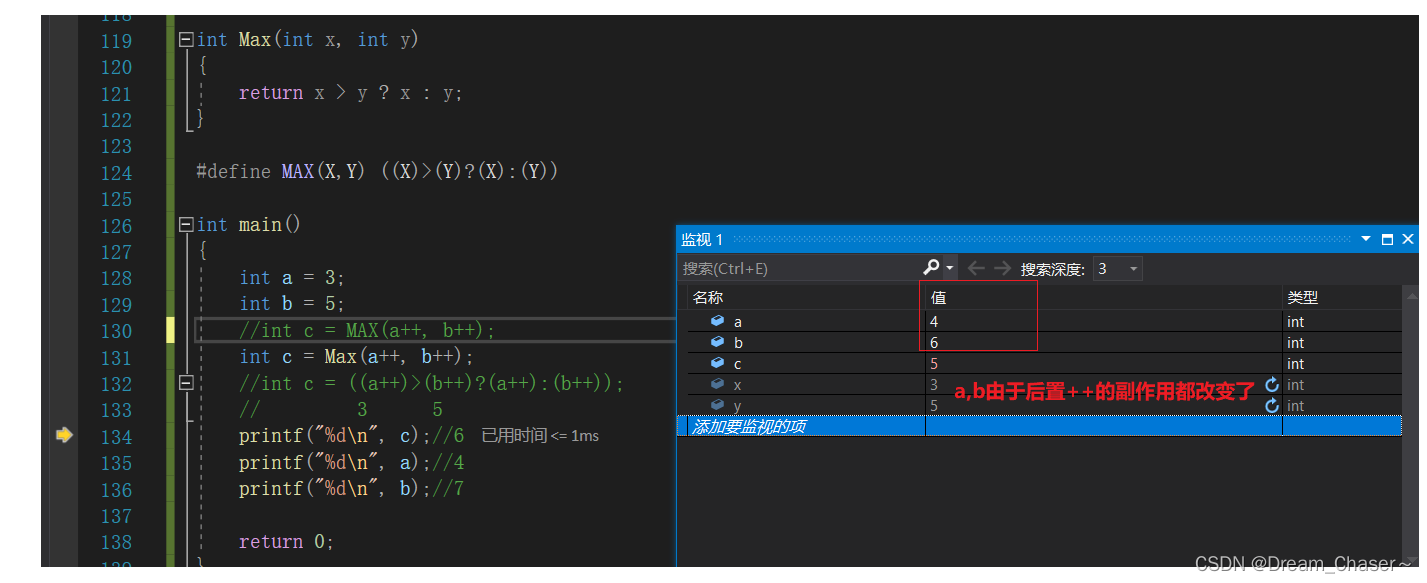
【C进阶】C程序是怎么运作的呢?-- 程序环境和预处理(上)
前言: 由于c语言的程序编译链接的这块知识点不清楚,回来复习一遍,以便于好理解c知识,我会尽快更新下一篇文章。 目录 1.程序的翻译环境和执行环境 2.翻译环境(编译链接) 编译(编译器…...

点滴生活记录1
2023/10/10 今天骑小电驴上班,带着小鸭子一起。路上的时候,我给小鸭子说,你要帮我看着点路,有危险的时候提醒我,也就刚说完没几分钟,一个没注意,直接撞到一个拦路铁墩子上,车子连人歪…...

gitea仓库迁移
(1)先安装git,再直接将源机器上的gitea文件夹复制到新机器上。这样原始数据及账号信息都还在。 (2)根据实际情况修改gitea\custom\conf\app.ini文件夹下app.ini文件的相关路径。 (3)如下命令启…...
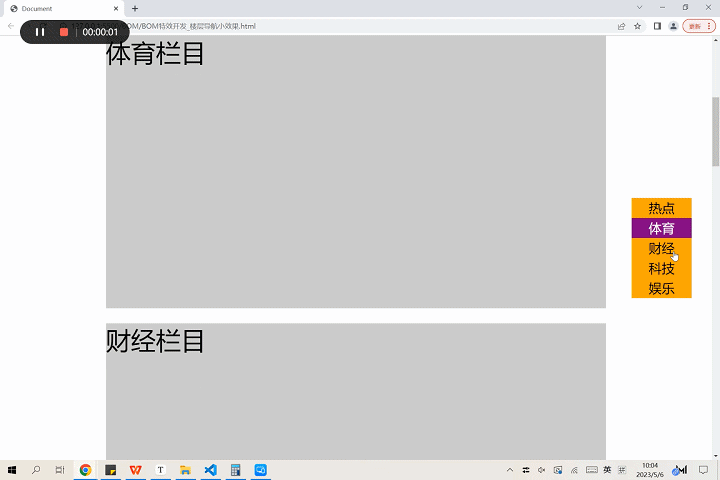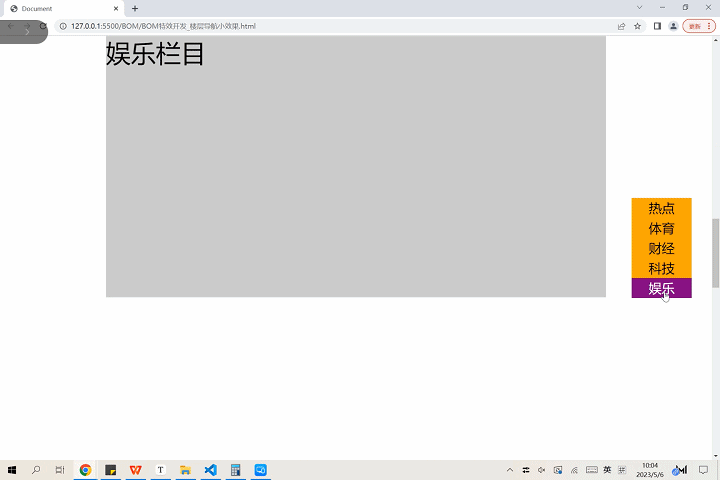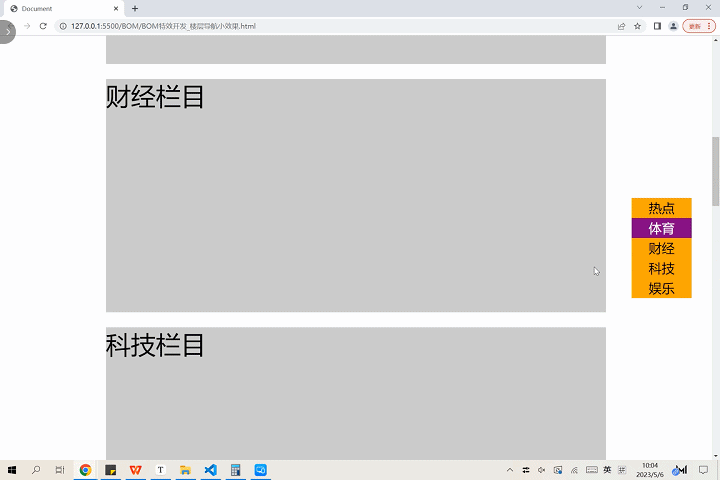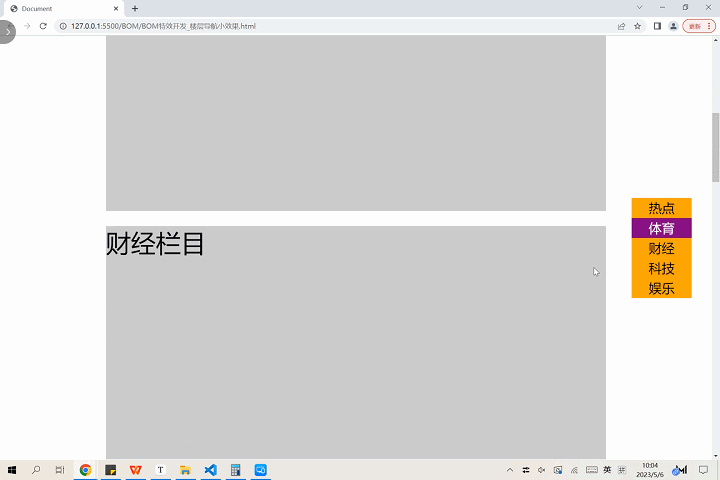
〖大前端 - 基础入门三大核心之JS篇㊽〗- BOM特效开发
说明:该文属于 大前端全栈架构白宝书专栏,目前阶段免费,如需要项目实战或者是体系化资源,文末名片加V!作者:哈哥撩编程,十余年工作经验, 从事过全栈研发、产品经理等工作,目前在公司…...

【扩散模型】ControlNet从原理到实战
ControlNet从原理到实战 ControlNet原理ControlNet应用于大型预训练扩散模型ControlNet训练过程ControlNet示例1 ControlNet与Canny Edge2. ControlNet与Depth3. ControlNet与M-LSD Lines4. ControlNet与HED Boundary ControlNet实战Canny Edge实战Open Pose 小结参考资料 Cont…...

AI并行计算:CUDA和ROCm
1 介绍 1.1 CUDA CUDA(Compute Unified Device Architecture)是Nvidia于2006年推出的一套通用并行计算架构,旨在解决在GPU上的并行计算问题。其易用性和便捷性能够方便开发者方便的进行GPU编程,充分利用GPU的并行能力࿰…...

2023五岳杯量子计算挑战赛数学建模思路+代码+模型+论文
目录 计算力网络(CPN)是一种新型的信息基础设施,完整论文代码见文末 问题描述 2.1 问题1 2.2 问题2 2.3 问题3 问题1的解答过程: 问题3的解答过程: 决策优化应用场景:人工智能模型超参数调优 背景信…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...

