LeetCode-面试题 05.02. 二进制数转字符串【数学,字符串,位运算】
LeetCode-面试题 05.02. 二进制数转字符串【数学,字符串,位运算】
- 题目描述:
- 解题思路一:简单暴力。小数点后面的二进制,now首先从0.5开始之和每次除以2。然后依次判断当前数是否大于now,是则答案加1。若等于now则可以直接返回。小于则答案加0。其实就是一个不断迭代计算小数的过程。
- 解题思路二:不断×2,左进一位,依次判断是0还是1。
- 解题思路三:0
题目描述:
二进制数转字符串。给定一个介于0和1之间的实数(如0.72),类型为double,打印它的二进制表达式。如果该数字无法精确地用32位以内的二进制表示,则打印“ERROR”。
示例1:
输入:0.625
输出:“0.101”
示例2:
输入:0.1
输出:“ERROR”
提示:0.1无法被二进制准确表示
提示:
32位包括输出中的 “0.” 这两位。
题目保证输入用例的小数位数最多只有 6 位
https://leetcode.cn/problems/bianry-number-to-string-lcci/description/
解题思路一:简单暴力。小数点后面的二进制,now首先从0.5开始之和每次除以2。然后依次判断当前数是否大于now,是则答案加1。若等于now则可以直接返回。小于则答案加0。其实就是一个不断迭代计算小数的过程。
class Solution {
public:string printBin(double num) {string ans="0.";double now=0.5;while(num>0){if(num>now){num-=now;ans+="1";}else if(now==num){ans+="1";return ans;}else{ans+="0";}if(now<0.0000001) return "ERROR";//题目保证输入用例的小数位数最多只有 6 位now/=2; }return "ERROR";}
};
时间复杂度:O(1)//加上剪枝的话最多循环6次
空间复杂度:O©//字符串。
解题思路二:不断×2,左进一位,依次判断是0还是1。
当 num的十进制的小数位数最多只有 6 位时,若 num 能表示为有限位二进制小数,则二进制的小数位数同样至多为 6 位。
证明见传送门!!!
class Solution {
public:string printBin(double num) {string bin = "0.";for (int i = 0; i < 6; ++i) { // 至多循环 6 次num *= 2;if (num < 1)bin += '0';else {bin += '1';if (--num == 0)return bin;}}return "ERROR";}
};
时间复杂度:O(1)//加上剪枝的话最多循环6次
空间复杂度:O(1)//字符串。
解题思路三:0
相关文章:

LeetCode-面试题 05.02. 二进制数转字符串【数学,字符串,位运算】
LeetCode-面试题 05.02. 二进制数转字符串【数学,字符串,位运算】题目描述:解题思路一:简单暴力。小数点后面的二进制,now首先从0.5开始之和每次除以2。然后依次判断当前数是否大于now,是则答案加1。若等于…...
pandas: 三种算法实现递归分析Excel中各列相关性
目录 前言 目的 思路 代码实现 1. 循环遍历整个SDGs列,两两拿到数据 2. 调用pandas库函数直接进行分析 完整源码 运行效果 总结 前言 博主之前刚刚被学弟邀请参与了2023美赛,这也是第一次正式接触数学建模竞赛,现在已经提交等待结果…...

【Python百日进阶-Web开发-Vue3】Day543 - Vue3 商城后台 03:登录页面初建
文章目录 一、创建登录页面 login.vue二、登录页面响应式处理,以适应不同大小的屏幕2.1 element-plus 的layout布局中关于响应式的说明2.2 修改login.vue文件2.2.1 :lg=16 大于1200px 横排 2:12.2.2 :md=12 大于992小于1200px 横排 1:12.2.3 小于992 竖排三、引入Element-plus…...
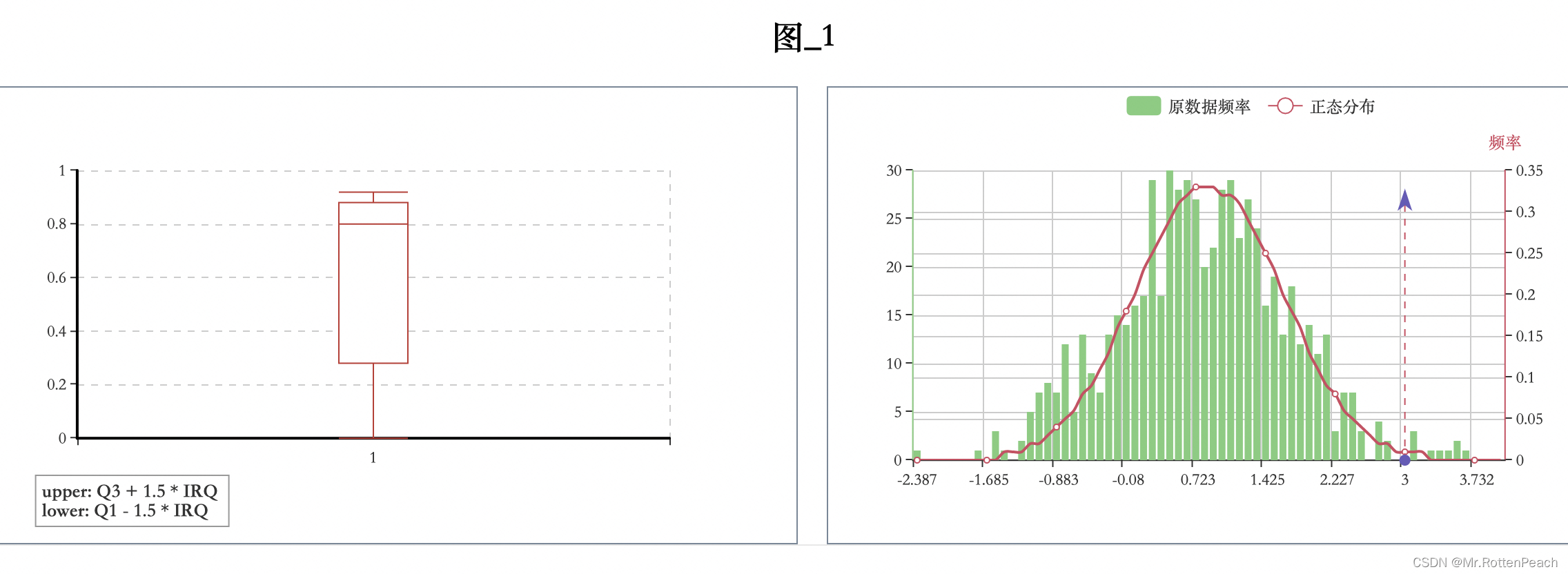
python画直方图,刻画数据分布
先展示效果 准备一维数据 n 个数据元素计算最大值,最小值、均值、标准差、以及直方图分组 import numpy as np data list() for i in range(640):data.append(np.random.normal(1)) print(data)z np.histogram(data, bins64) print(list(z[0])) ### 对应 x 轴数据…...
【学数学关键是要学会在什么情况下,知道使用什么工具。】)
几何学小课堂:非欧几何(广义相对论采用黎曼几何作为数学工具)【学数学关键是要学会在什么情况下,知道使用什么工具。】
文章目录 引言I 非欧几何1.1 黎曼几何1.2 共形几何1.3 罗氏几何II 黎曼几何的应用2.1 广义相对论2.2 超弦III 理解不同的几何体系的共存3.1 更扎实的欧氏几何3.2 殊途同归引言 公理有错会得到两种情况: 如果某一条自己设定的新公理和现有的公理相矛盾,那么相应的知识体系就建…...

Ubuntu配置静态IP的方法
Ubuntu配置静态IP的方法前言一、查看虚机分配的网卡IP二、查看网卡的网关IP三、配置静态IP1.配置IPv4地址2.执行netplan apply使改动生效3.配置的网卡未生效,修改50-cloud-init.yaml文件解决4.测试vlan网络通信总结前言 Ubuntu18.04 欧拉环境 vlan网络支持ipv6场景…...

90%的人都不算会爬虫,这才是真正的技术,从0到高手的进阶
很多人以为学会了urlib模块和xpath等几个解析库,学了Selenium就会算精通爬虫了,但到外面想靠爬虫技术接点私活,才发现寸步难行。 龙叔我做了近20年的程序员,今天就告诉你,真正的爬虫高手应该学哪些东西,就…...

排序之损失函数List-wise loss(系列3)
排序系列篇: 排序之指标集锦(系列1)原创 排序之损失函数pair-wise loss(系列2)排序之损失函数List-wise loss(系列3) 最早的关于list-wise的文章发表在Learning to Rank: From Pairwise Approach to Listwise Approach中,后面陆陆续续出了各种变形&#…...

js对象和原型、原型链的关系
JS的原型、原型链一直是比较难理解的内容,不少初学者甚至有一定经验的老鸟都不一定能完全说清楚,更多的"很可能"是一知半解,而这部分内容又是JS的核心内容,想要技术进阶的话肯定不能对这个概念一知半解,碰到…...
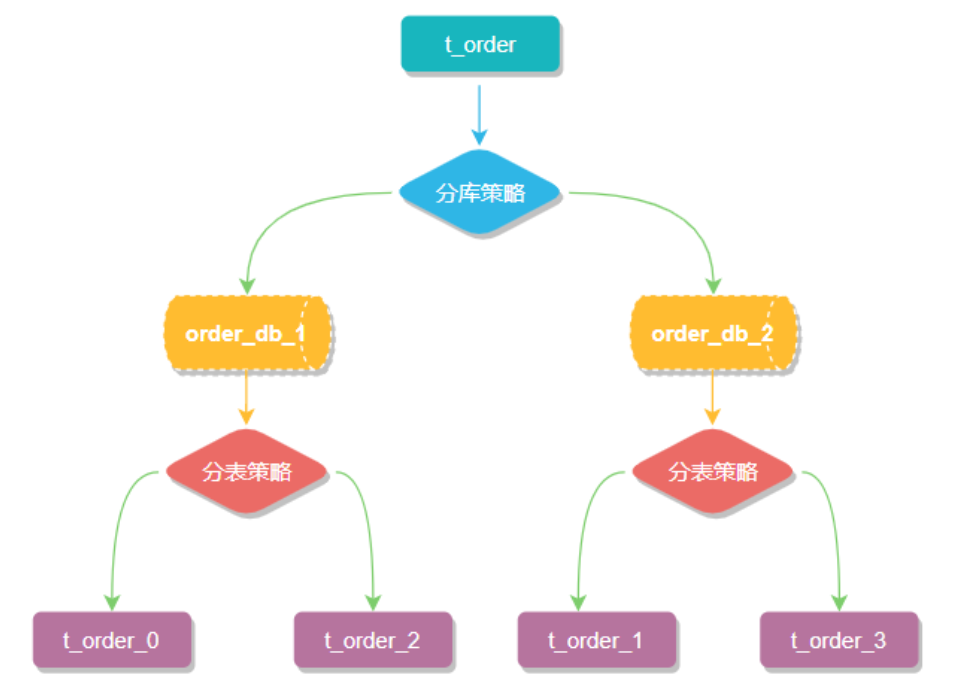
【SpringBoot高级篇】SpringBoot集成Sharding-JDBC分库分表
【SpringBoot高级篇】SpringBoot集成Sharding-JDBC分库分表Apache ShardingSphere分库分表分库分表的方式垂直切分垂直分表垂直分库水平切分水平分库水平分表分库分表带来的问题分库分表中间件Sharding-JDBCsharding-jdbc实现水平分表sharding-jdbc实现水平分库sharding-jdbc实…...

Shell特殊字符
shell语言,一些字符是有特殊意义的。 根据作用分为几种特殊符号 一、空白 shell调用函数,不像c语言那样用把参数放到括号里,用逗号分隔。而是用空格作为参数之间,参数与函数名之间的分隔符。 换行符也是特殊字符。换行符用作一条命…...

【计算机二级python】综合题目
计算机二级python真题 文章目录计算机二级python真题一、德国工业战略规划二、德国工业战略规划 第一问三、德国工业战略规划 第二问一、德国工业战略规划 描述:在右侧答题模板中修改代码,删除代码中的横线,填写代码,完成考试答案。…...

字节直播leader面
设计评论系统(缓存怎么做) mysql是否有主从延迟,如何解决 mysql有主从延迟 主从延迟主要因为mysql主从同步的机制,mysql有三种同步机制 同步复制:事务线程等待所有从库复制成功响应异步复制:事务不等待…...

PIC 单片机的时钟
注意:本文的内容无法保证绝对精确,后续可能会做改动,只是自己的笔记。这里的资料均源自数据手册本身。PIC18系列单片机的参考时钟可以选择三个基础时钟源:Primary Clock, OSC1 or OSC2,Secondary Clock,Inner clock.时钟源分为两个…...
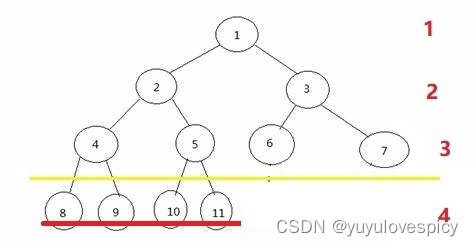
【数据结构】关于二叉树你所应该知道的数学秘密
目录 1.什么是二叉树(可以跳过 目录跳转) 2.特殊的二叉树(满二叉树/完全二叉树) 2.1 基础知识 2.2 满二叉树 2.3 完全二叉树 3.二叉树的数学奥秘(主体) 3.1 高度与节点个数 3.2* 度 4.运用二叉树的…...

哈希表题目:猜数字游戏
文章目录题目标题和出处难度题目描述要求示例数据范围解法一思路和算法代码复杂度分析解法二思路和算法代码复杂度分析题目 标题和出处 标题:猜数字游戏 出处:299. 猜数字游戏 难度 4 级 题目描述 要求 你在和朋友一起玩猜数字(Bulls…...
项目请求地址自动加上了本地ip的解决方式
一般情况下来说都是一些粗心大意的问题导致的 场景一:少加了/ 场景二:前后多加了空格 场景三:拼接地址错误
Vue3 企业级项目实战:项目须知与课程约定
本节内容很重要,希望大家能够耐心看完。 Vue3 企业级项目实战 - 程序员十三 - 掘金小册Vue3 Element Plus Spring Boot 企业级项目开发,升职加薪,快人一步。。「Vue3 企业级项目实战」由程序员十三撰写,2744人购买https://s.ju…...

传导EMI抑制-Π型滤波器设计
1 传导电磁干扰简介 在开关电源中,开关管周期性的通断会产生周期性的电流突变(di/dt)和电压突变(dv/dt),周期性的电流变化和电压变化则会导致电磁干扰的产生。 图1所示为Buck电路的电流变化,在Buck电路中上管电流和下…...

如何在excel中创建斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
