补档:红黑树代码实现+简略讲解
红黑树讲解和实现
- 1 红黑树介绍
- 1.1 红黑树特性
- 1.2 红黑树的插入
- 1.3 红黑树的删除
- 2 完整代码实现
- 2.1 rtbtree.h头文件
- 2.2 main.c源文件
1 红黑树介绍
红黑树( Red-Black tree,简称RB树)是一种自平衡二叉查找树,是计算机科学中常见的一种数据结构,其典型用途是实现关联数组。红黑树的结构复杂,但其操作有着良好的最坏情况运行时间,且在实践中有着较高的效率:它可以在O(log2n)时间内完成查找、插入和删除操作,其中的n是树中结点的数量。
红黑树(RB树)是二叉树中重要的知识点,因为在操作系统的内核中、C++的STL和Java的数据结构中都大量使用了红黑树,红黑树的增删查改的复杂度均为log2n。
1.1 红黑树特性
红黑树是每个结点都带有颜色属性的二叉查找树,颜色为红色或黑色,给结点进行染色的原因是用颜色和红黑树性质对树进行平衡,使得红黑树的任意一条路径长度都不可能超过其他路径的两倍。在二叉查找树的–般要求以外,对于任何有效的红黑树,我们额外增加了如下性质:
- 结点是红色的或黑色的。
- 根是黑色的。
- 所有叶子结点都是黑色的(叶子是NIL结点)。
- 每个红色结点必须有两个黑色的子结点(从每个叶子到根的所有路径上不能有两个连续的红色结点)。
- 从任意一个点到其每个叶子的所有简单路径都包含相同数量的黑色结点。
王道408考研的咸鱼学长总结了一个口诀:左根右、根叶黑、不红红、黑路同。
1.2 红黑树的插入
红黑树的插入结点,首先标记为红色,按照二叉排序树的方式插入后再做调整。红黑树的插入分为5种情况。
**情形一:**新结点N是树根没有子节点。这种空树的情况,直接将新结点作为根插入染成黑色即可。具体代码如下:
void insert_case1(node *n)
{if(n->parent == NULL)//如果新插入结点没有父结点,即此结点为根结点n->color = BLACK;//直接染黑else insert_case2(n);//否则转入情形2,即有父结点的情况
}
**情形二:**父结点为黑色,则直接将新结点插入,满足性质四不红红(即没有两个连续红色)。还满足性质5,不会增减该路径上黑色结点的数量。具体代码如下:
void insert_case2(node *n)
{if(n->parent->color == BLACK) //如果父结点为黑色,则直接插入return; //不需要调整else insert_case3(n); //如果父结点为红色,则需要调整
}
**情形三:**如果父结点和叔结点都是红色的,那么我们可以将父结点和叔结点都染黑(保证不红红性质4),然后将爷结点染红,插入的子结点仍然是红色(满足路黑同性质5)。此时需要考虑爷结点是否为根结点,如果爷结点为根结点,则需要将爷结点染黑,保证性质不变,如果爷结点不为根结点,则向上将爷结点(红)作为其父结点的新插入结点,递归情形一。下面给出图示和实现代码:
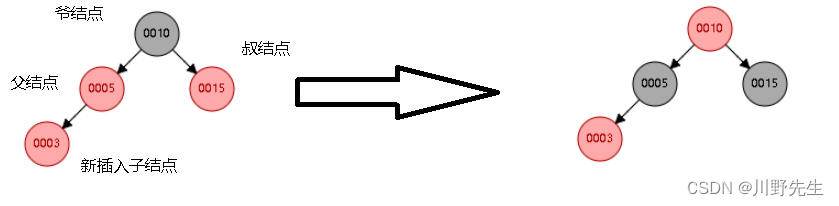
void insert_case3(node *n)
{if(uncle(n)!=NULL && uncle(n)->color == RED && n->parent->color == RED){//这里父结点颜色可以不考虑,否则违反黑路同性质5,为了和算法描述一致,也加入判断n->parent->color = BLACK;//将父结点染黑uncle(n)->color = BLACK;//将叔结点染黑grandparent(n)->color = RED;//将爷结点染红insert_case1(grandparent(n));//将红色的爷结点作为新结点,对上级进行调整}else insert_case4(n);//不满足情形3,则考虑情形4
}
**情形四:**父结点是红色,叔结点是黑色或者缺少的情况,并且新结点是父结点的右子节点,而父结点又是爷结点的左子节点。这种情况需要左旋调换新结点和父结点。
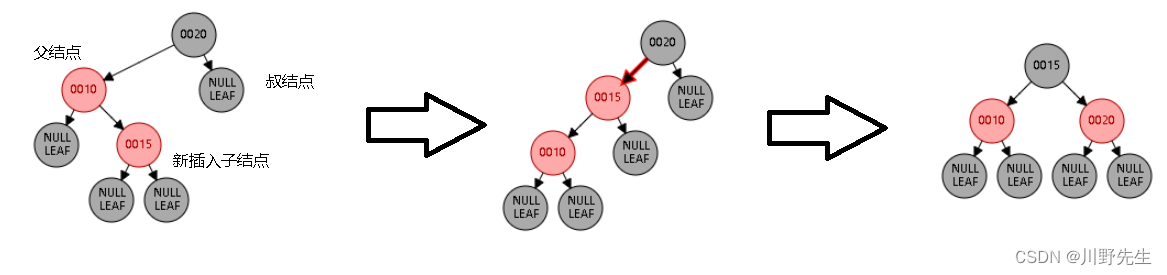
void insert_case4(node *n)
{if(n == n->parent->right && n->parent == grandparent(n)->left){roate_left(n->parent);n = n->left;}else if(n->parent->left && n->parent == grandparent(n)->right){rotate_right(n->parent);//上图中对称的情况父结点在爷结点右边,子结点在父结点左边n = n->right;}insert_case5(n);//情形5
}
**情形五:**父结点是红色,叔结点是黑色或缺少,子结点是父节点的左子节点,而父结点又是爷结点的左下结点。这种情况需要将爷结点右旋,并且改变相应结点的颜色完成插入。
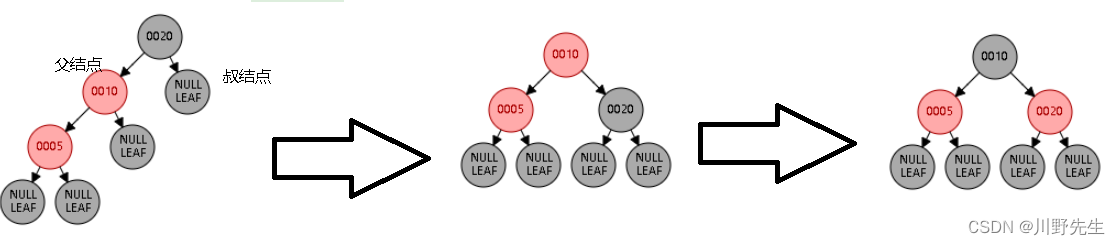
void insert_case5(node *n)
{n->parent->color = BLACK;grandparent(n)->color = RED;if(n->parent->left == n && n->parent == grandparent(n)->left){rotate_right(grandparent(n));}else if(n->parent->right == n && n->parent == grandparent(n)->right){//与上图中完全对称的情况rotate_left(grparent(n);}
}
插入修正函数: 对于上述情景3、4、5,红黑树插入结点后,可能会失去平衡,调用此函数保持性质。对于下图中情形三可以单独处理,而情形四可以通过旋转到情形五,进而调整。
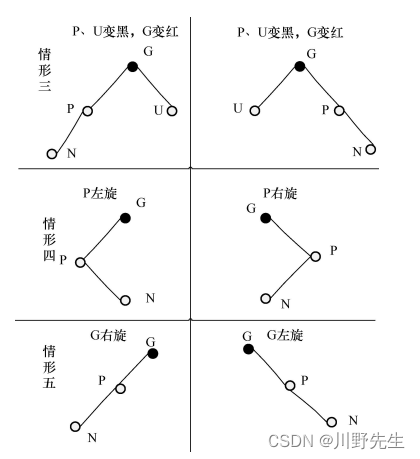
static void rbtree_insert_fixup(RBRoot *root, Node *node)
{Node *parent,*gparent;//如果父结点存在且为红色需要调整while((parent = rb_parent(node)) && rb_is_red(parent)){gparent = rb_parent(parent);//若父结点是爷结点的左孩子结点if(parent == gparent->left){//情况1条件:叔结点存在且为红色,这种是情形3Node *uncle = gparent->right;if(uncle && rb_is_red(uncle)){//将父结点和叔结点染黑,将爷结点染红rb_set_black(uncle);rb_set_black(parent);rb_set_red(gparent);node = gparent;//node调整完毕,回到父结点}}//情况2条件:叔结点是黑色或不存在,且当前结点是父节点的有孩子,情形4//父节点右旋,交换父子结点if (parent->right == node){Node *tmp;rbtree_left_rotate(root, parent);tmp = parent;parent = node;node = tmp;}//情形3条件:叔结点是黑色,且当前结点是父节点的左孩子结点。这里是情形 5rb_set_black(parent); //旋转前设置好颜色rb_set_red(gparent); //旋转前设置好颜色rbtree_right_rotate(root, gparent);//爷结点右旋} else{//若父结点是祖父结点的右孩子结点,则下面三种和上面的是对称的Node *uncle = gparent->left;if (uncle && rb_is_red(uncle)){rb_set_black(uncle);rb_set_black(parent);rb_set_red(gparent);node = gparent;continue; //继续进行调整}if (parent->left == node){Node *tmp;rbtree_right_rotate(root, parent);tmp = parent;parent = node;node = tmp;}//Case 3 条件:叔父结点是黑色的,且当前结点是右孩子结点。这里是情形 5rb_set_black(parent); //旋转前设置好颜色rb_set_red(gparent); //旋转前设置好颜色rbtree_left_rotate(root, gparent);}//将根结点设为黑色rb_set_black(root->node);
}
1.3 红黑树的删除
&emps;&emps;对于红黑树的删除中,考虑删除结点为黑色或红色,如果删除结点为红色则不需要做调整,正常删除,因为删除红色结点不会影响黑高。而删除黑色结点则比较复杂,需要考虑以下六种情形。
**注意:**接下来的删除讲解均按照此图进行,此图是指删除结点后红黑树,删除规则按照二叉平衡树的方式,之后未作其他的调整。我们把删除结点N后的替代的结点记为X。
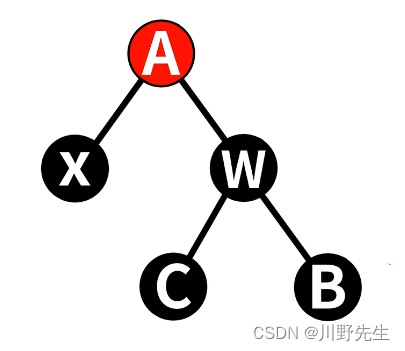
情形一: 红黑树仅有一个黑根,删除此根满足所有性质。代码如下:
void delete_case1(struct node *n)
{if(n->parent!=NULL)delete_case2(n);//如果删除的结点不是根
}
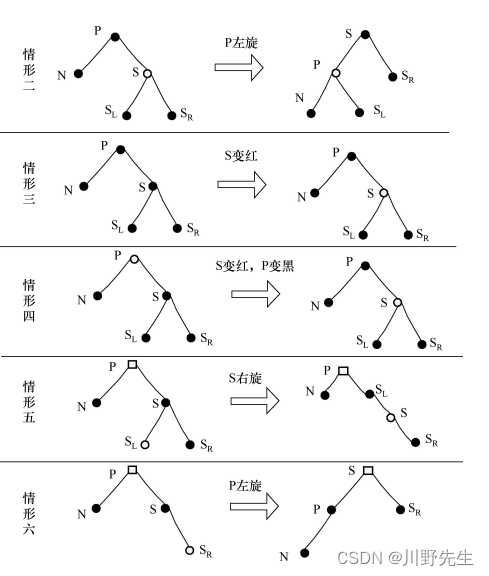
情形二: 被删除的黑色结点N,黑色结点X是N的顶替结点,X的兄弟结点W结点是红色。这种删除的情况会使左边黑高-1,破坏了黑路同性质5,所以需要做染色左旋操作。先将父结点染红,再将兄弟结点W染黑,然后对父结点进行左旋操作,这样不会破坏红黑树的性质。
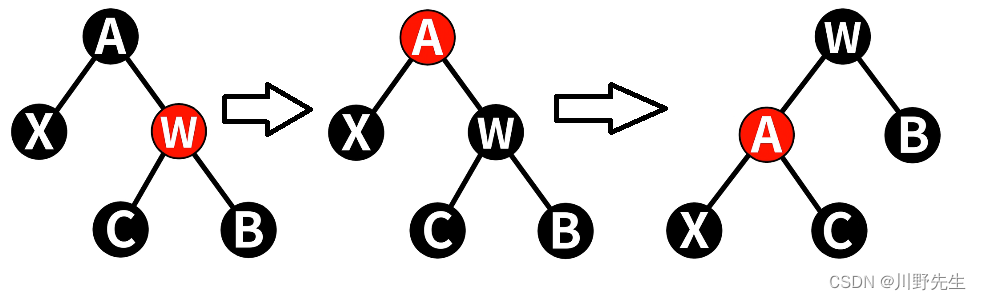
void delete_case2(struct node *n)
{struct node *s = sibling(n);//n的兄弟结点if(s->color == RED){//如果兄弟结点是红色n->parent->color = RED;//将父结点染红s->color = BLACK;//将父结点染黑if(n->parent->left == n)//如果n是左孩子rotate_ left(n->parent);//父结点左旋 else //如果n是右孩子rotate_right(n->parent);//父结点右旋}delete_case3(n);//考虑情景3}
情形三: 被删除的黑色结点N,黑色结点X是N的顶替结点,X的父结点、兄弟结点W及其子结点均为黑色。左侧黑高-1,破坏了黑路同性质5,此时将兄弟结点W染红,使得满足黑路同性质5,但是如果A树作为左子树或者右子树,整体黑高-1,此时需要将矛盾上移,在A结点上重新做平衡处理。代码如下:
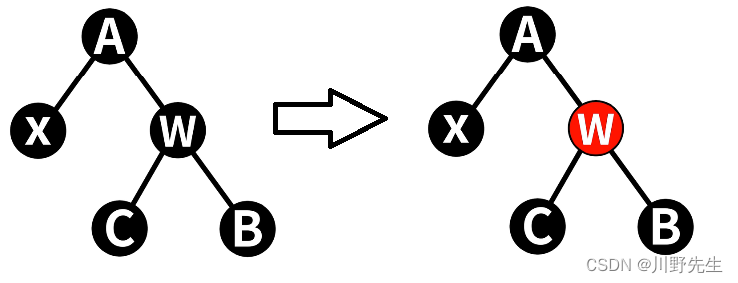
void delete_case3(struct node *n)
{struct node *s = sibling(n);if((n->parent->color == BLACK) && (S->color == BLACK) && (s->left->color == BLACK) && (s->right->color == BLACK)){s->color = RED;//将兄弟结点染红delete_case1(n->parent);//将父结点作为新的处理结点,从case1开始平衡}else delete_case4(n);//如果不符合情形三,请看情形4
}
**情形四:**被删除的黑色结点N,黑色结点X是N的顶替结点,父结点A是红色,兄弟结点W及其子结点都是黑色。此时左侧黑高-1,不满足黑路同性质5,所以需要调整,将父结点A染黑,兄弟结点W染红,则满足性质。代码如下:
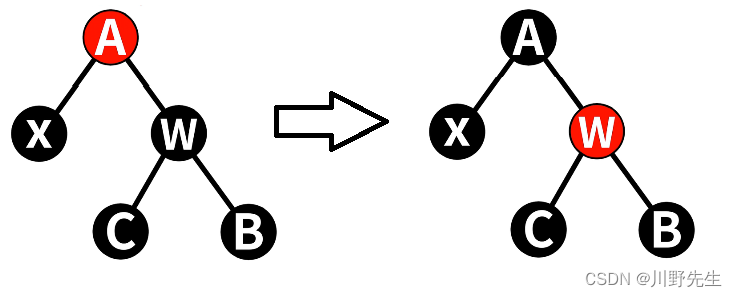
void delete_case4(struct node *n)
{struct node *s = sibling(n);if((n->parent->color == RED) && (S->color == BLACK) && (s->left->color == BLACK) && (s->right->color == BLACK)){s->color = RED;//将兄弟结点染红n->parent = BLACK;//将父结点染黑}else delete_case5(n);//如果不符合情形4,考虑情形五
}
情形五: 被删除的黑色结点N,黑色结点X是N的顶替结点,X的兄弟结点W是黑色,W结点的左子结点是红色,W结点的右子结点是黑色。此时将兄弟结点W染红,W的左子结点染黑,然后进行右旋操作,此时代替结点X和父结点A都不受右旋影响。然后继续情形六。代码如下:

void
delete_case5(struct node *n)
{struct node *s = sibling (n);if(s->color == BLACK){if((n == n->parent->left)&&(s->right->color == BLACK)&&(s->left->color == RED)) { // 这种情况下 n 结点是其父结点的左子结点,S 结点是其父结点的右子结s->color = RED;s->left->color = BLACK;rotate_right (s);} else if((n == n->parent->right)&&(s->left->color == BLACK)&&(s->right->color == RED)) {// 这种情况下 n 结点是其父结点的右子结点,S 结点是其父结点的左子结点s->color = RED;s->right->color = BLACK;rotate_left (s);}}delete_case6 (n); //调整完毕后,再通过情形 6 进行调整
}
情形六: 被删除的黑色结点N,黑色结点X是N的顶替结点,兄弟结点W结点是黑色的,W结点的右子结点是红色的,而替代结点X是其父结点A的左子结点。将兄弟结点W染红,将父结点A染黑,W的右子结点也染黑,然后W左旋操作。就达到了情形四的情况。代码如下:
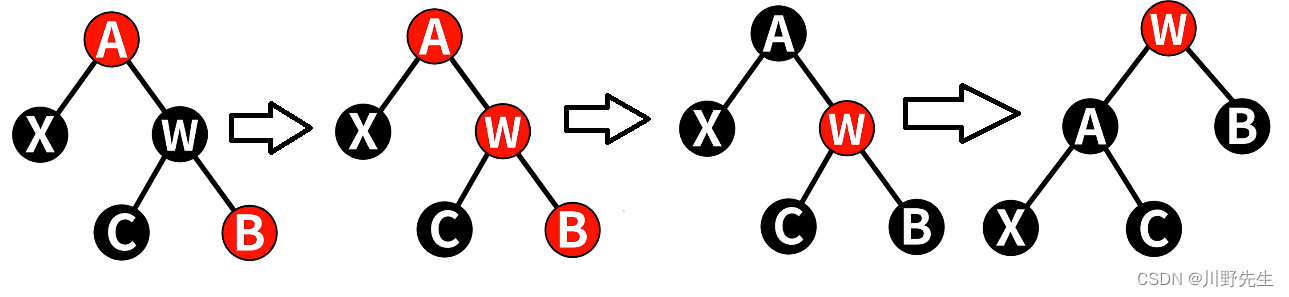
void delete_case6(struct node *n)
{struct node *s = sibling(n);s->color = n->parent->color;n->parent->color = BLACK;if(n->parent->left==n){s->right->color = BLACK;rotate_left(n->parent);}else{s->left->color = BLACK;rotate_right(n->parent);}
}
删除修正函数:
static void rbtree_delete_fixup(RBRoot *root, Node *node, Node *parent)
{Node *other;//下面的x说的是nodewhile ((!node || rb_is_black(node)) && node != root->node){if (parent->left == node){//删除other = parent->right;if (rb_is_red(other)){// Case 1: x的兄弟w是红色的,删除77 rb_set_black(other);rb_set_red(parent);rbtree_left_rotate(root, parent);other = parent->right;}if ((!other->left || rb_is_black(other->left)) &&(!other->right || rb_is_black(other->right))){// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的,删除65时,删除82时,二级进入循环rb_set_red(other);node = parent;parent = rb_parent(node);}else{if (!other->right || rb_is_black(other->right)){// Case 3: x的兄弟w是黑色的,并且w的右孩子为黑色。 rb_set_black(other->left);rb_set_red(other);rbtree_right_rotate(root, other);other = parent->right;}// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。rb_set_color(other, rb_color(parent));rb_set_black(parent);rb_set_black(other->right);rbtree_left_rotate(root, parent);node = root->node;break;}}else{//删除other = parent->left;if (rb_is_red(other)){// Case 1: x的兄弟w是红色的 rb_set_black(other);rb_set_red(parent);rbtree_right_rotate(root, parent);other = parent->left;}if ((!other->left || rb_is_black(other->left)) &&(!other->right || rb_is_black(other->right))){// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的,删除77 rb_set_red(other);node = parent;parent = rb_parent(node);}else{if (!other->left || rb_is_black(other->left)){//删除99时,应该是w的左孩子是黑色// Case 3: x的兄弟w是黑色的,并且w的左孩子是为黑色。 rb_set_black(other->right);rb_set_red(other);rbtree_left_rotate(root, other);other = parent->left;}// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。rb_set_color(other, rb_color(parent));rb_set_black(parent);rb_set_black(other->left);rbtree_right_rotate(root, parent);node = root->node;break;}}}if (node)rb_set_black(node);
}
2 完整代码实现
2.1 rtbtree.h头文件
#ifndef _RED_BLACK_TREE_H_
#define _RED_BLACK_TREE_H_#define RED 0 // 红色节点
#define BLACK 1 // 黑色节点typedef int Type;// 红黑树的节点
typedef struct RBTreeNode{unsigned char color; // 颜色(RED 或 BLACK)Type key; // 关键字(键值)struct RBTreeNode *left; // 左孩子struct RBTreeNode *right; // 右孩子struct RBTreeNode *parent; // 父结点
}Node, *RBTree;// 红黑树的根
typedef struct rb_root{Node *node;
}RBRoot;// 创建红黑树,返回"红黑树的根"!
RBRoot* create_rbtree();// 销毁红黑树
void destroy_rbtree(RBRoot *root);// 将结点插入到红黑树中。插入成功,返回0;失败返回-1。
int insert_rbtree(RBRoot *root, Type key);// 删除结点(key为节点的值)
void delete_rbtree(RBRoot *root, Type key);// 前序遍历"红黑树"
void preorder_rbtree(RBRoot *root);
// 中序遍历"红黑树"
void inorder_rbtree(RBRoot *root);
// 后序遍历"红黑树"
void postorder_rbtree(RBRoot *root);// (递归实现)查找"红黑树"中键值为key的节点。找到的话,返回0;否则,返回-1。
int rbtree_search(RBRoot *root, Type key);
// (非递归实现)查找"红黑树"中键值为key的节点。找到的话,返回0;否则,返回-1。
int iterative_rbtree_search(RBRoot *root, Type key);// 返回最小结点的值(将值保存到val中)。找到的话,返回0;否则返回-1。
int rbtree_minimum(RBRoot *root, int *val);
// 返回最大结点的值(将值保存到val中)。找到的话,返回0;否则返回-1。
int rbtree_maximum(RBRoot *root, int *val);// 打印红黑树
void print_rbtree(RBRoot *root);#endif
2.2 main.c源文件
/*** C语言实现的红黑树(Red Black Tree)** @author skywang* @date 2013/11/18*/#include <stdio.h>
#include <stdlib.h>
#include "rbtree.h"#define rb_parent(r) ((r)->parent)
#define rb_color(r) ((r)->color)
#define rb_is_red(r) ((r)->color==RED)
#define rb_is_black(r) ((r)->color==BLACK)
#define rb_set_black(r) do { (r)->color = BLACK; } while (0)
#define rb_set_red(r) do { (r)->color = RED; } while (0)
#define rb_set_parent(r,p) do { (r)->parent = (p); } while (0)
#define rb_set_color(r,c) do { (r)->color = (c); } while (0)/** 创建红黑树,返回"红黑树的根"!*/
RBRoot* create_rbtree()
{RBRoot *root = (RBRoot *)malloc(sizeof(RBRoot));root->node = NULL;return root;
}/** 前序遍历"红黑树"*/
static void preorder(RBTree tree)
{if(tree != NULL){printf("%d ", tree->key);preorder(tree->left);preorder(tree->right);}
}
void preorder_rbtree(RBRoot *root)
{if (root)preorder(root->node);
}/** 中序遍历"红黑树"*/
static void inorder(RBTree tree)
{if(tree != NULL){inorder(tree->left);printf("%d ", tree->key);inorder(tree->right);}
}void inorder_rbtree(RBRoot *root)
{if (root)inorder(root->node);
}/** 后序遍历"红黑树"*/
static void postorder(RBTree tree)
{if(tree != NULL){postorder(tree->left);postorder(tree->right);printf("%d ", tree->key);}
}void postorder_rbtree(RBRoot *root)
{if (root)postorder(root->node);
}/** (递归实现)查找"红黑树x"中键值为key的节点*/
static Node* search(RBTree x, Type key)
{if (x==NULL || x->key==key)return x;if (key < x->key)return search(x->left, key);elsereturn search(x->right, key);
}
int rbtree_search(RBRoot *root, Type key)
{if (root)return search(root->node, key)? 0 : -1;
}/** (非递归实现)查找"红黑树x"中键值为key的节点*/
static Node* iterative_search(RBTree x, Type key)
{while ((x!=NULL) && (x->key!=key)){if (key < x->key)x = x->left;elsex = x->right;}return x;
}
int iterative_rbtree_search(RBRoot *root, Type key)
{if (root)return iterative_search(root->node, key) ? 0 : -1;
}/* * 查找最小结点:返回tree为根结点的红黑树的最小结点。*/
static Node* minimum(RBTree tree)
{if (tree == NULL)return NULL;while(tree->left != NULL)tree = tree->left;return tree;
}int rbtree_minimum(RBRoot *root, int *val)
{Node *node;if (root)node = minimum(root->node);if (node == NULL)return -1;*val = node->key;return 0;
}/* * 查找最大结点:返回tree为根结点的红黑树的最大结点。*/
static Node* maximum(RBTree tree)
{if (tree == NULL)return NULL;while(tree->right != NULL)tree = tree->right;return tree;
}int rbtree_maximum(RBRoot *root, int *val)
{Node *node;if (root)node = maximum(root->node);if (node == NULL)return -1;*val = node->key;return 0;
}/* * 找结点(x)的后继结点。即,查找"红黑树中数据值大于该结点"的"最小结点"。*/
static Node* rbtree_successor(RBTree x)
{// 如果x存在右孩子,则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。if (x->right != NULL)return minimum(x->right);// 如果x没有右孩子。则x有以下两种可能:// (01) x是"一个左孩子",则"x的后继结点"为 "它的父结点"。// (02) x是"一个右孩子",则查找"x的最低的父结点,并且该父结点要具有左孩子",找到的这个"最低的父结点"就是"x的后继结点"。Node* y = x->parent;while ((y!=NULL) && (x==y->right)){x = y;y = y->parent;}return y;
}/* * 找结点(x)的前驱结点。即,查找"红黑树中数据值小于该结点"的"最大结点"。*/
static Node* rbtree_predecessor(RBTree x)
{// 如果x存在左孩子,则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。if (x->left != NULL)return maximum(x->left);// 如果x没有左孩子。则x有以下两种可能:// (01) x是"一个右孩子",则"x的前驱结点"为 "它的父结点"。// (01) x是"一个左孩子",则查找"x的最低的父结点,并且该父结点要具有右孩子",找到的这个"最低的父结点"就是"x的前驱结点"。Node* y = x->parent;while ((y!=NULL) && (x==y->left)){x = y;y = y->parent;}return y;
}/* * 对红黑树的节点(x)进行左旋转** 左旋示意图(对节点x进行左旋):* px px* / /* x y * / \ --(左旋)--> / \ #* lx y x ry * / \ / \* ly ry lx ly ***/
static void rbtree_left_rotate(RBRoot *root, Node *x)
{// 设置x的右孩子为yNode *y = x->right;// 将 “y的左孩子” 设为 “x的右孩子”;// 如果y的左孩子非空,将 “x” 设为 “y的左孩子的父亲”x->right = y->left;if (y->left != NULL)y->left->parent = x;// 将 “x的父亲” 设为 “y的父亲”y->parent = x->parent;if (x->parent == NULL)//修改红黑树的根节点{//tree = y; // 如果 “x的父亲” 是空节点,则将y设为根节点root->node = y; // 如果 “x的父亲” 是空节点,则将y设为根节点}else{if (x->parent->left == x) x->parent->left = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”elsex->parent->right = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”}// 将 “x” 设为 “y的左孩子”y->left = x;// 将 “x的父节点” 设为 “y”x->parent = y;
}/* * 对红黑树的节点(y)进行右旋转** 右旋示意图(对节点y进行左旋):* py py* / /* y x * / \ --(右旋)--> / \ #* x ry lx y * / \ / \ #* lx rx rx ry* */
static void rbtree_right_rotate(RBRoot *root, Node *y)
{// 设置x是当前节点的左孩子。Node *x = y->left;// 将 “x的右孩子” 设为 “y的左孩子”;// 如果"x的右孩子"不为空的话,将 “y” 设为 “x的右孩子的父亲”y->left = x->right;if (x->right != NULL)x->right->parent = y;// 将 “y的父亲” 设为 “x的父亲”x->parent = y->parent;if (y->parent == NULL) {//tree = x; // 如果 “y的父亲” 是空节点,则将x设为根节点root->node = x; // 如果 “y的父亲” 是空节点,则将x设为根节点}else{if (y == y->parent->right)y->parent->right = x; // 如果 y是它父节点的右孩子,则将x设为“y的父节点的右孩子”elsey->parent->left = x; // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”}// 将 “y” 设为 “x的右孩子”x->right = y;// 将 “y的父节点” 设为 “x”y->parent = x;
}/** 红黑树插入修正函数** 在向红黑树中插入节点之后(失去平衡),再调用该函数;* 目的是将它重新塑造成一颗红黑树。** 参数说明:* root 红黑树的根* node 插入的结点 // 对应《算法导论》中的z*/
static void rbtree_insert_fixup1(RBRoot *root, Node *node)
{Node *parent, *gparent;// 若“父节点存在,并且父节点的颜色是红色”while ((parent = rb_parent(node)) && rb_is_red(parent)){gparent = rb_parent(parent);//若“父节点”是“祖父节点的左孩子”if (parent == gparent->left){// Case 1条件:叔叔节点是红色{Node *uncle = gparent->right;if (uncle && rb_is_red(uncle))//没有节点进入该分支,如何构造?{rb_set_black(uncle);rb_set_black(parent);rb_set_red(gparent);node = gparent;continue;}}// Case 2条件:叔叔是黑色,且当前节点是右孩子,叔叔不存在,也认为是黑色if (parent->right == node)//插入80节点时,先左旋,后右旋{Node *tmp;rbtree_left_rotate(root, parent);tmp = parent;parent = node;node = tmp;}// Case 3条件:叔叔是黑色,且当前节点是左孩子。rb_set_black(parent);//旋转前设置好颜色rb_set_red(gparent);//旋转前设置好颜色rbtree_right_rotate(root, gparent);} else//若父节点是祖父节点的右孩子{// Case 1条件:叔叔节点是红色{Node *uncle = gparent->left;//当插入60时,调整颜色即可,调整颜色后不符合红黑树,递归进行if (uncle && rb_is_red(uncle)){rb_set_black(uncle);rb_set_black(parent);rb_set_red(gparent);node = gparent;continue;//继续进行调整}}// Case 2条件:叔叔是黑色,且当前节点是左孩子,插入30时,先右旋,后左旋if (parent->left == node){Node *tmp;rbtree_right_rotate(root, parent);tmp = parent;parent = node;node = tmp;}// Case 3条件:叔叔是黑色,且当前节点是右孩子。rb_set_black(parent);//旋转前设置好颜色rb_set_red(gparent);//旋转前设置好颜色rbtree_left_rotate(root, gparent);}}// 将根节点设为黑色rb_set_black(root->node);
}static void rbtree_insert_fixup(RBRoot *root, Node *node)
{Node* parent;Node *tmp;while((parent = rb_parent(node))&&parent->color==RED){Node *gparent=rb_parent(parent);if(gparent->left==parent){//情形三Node *uncle=gparent->right;if(uncle&&rb_is_red(uncle)){rb_set_black(parent);rb_set_black(uncle);rb_set_red(gparent);node=gparent;continue;}//情形四if(parent->right==node){rbtree_left_rotate(root,parent);tmp=parent;parent=node;node=tmp;}//情形五rbtree_right_rotate(root,gparent);rb_set_black(parent);rb_set_red(gparent);}else{//情形三Node *uncle=gparent->left;if(uncle&&rb_is_red(uncle)){rb_set_black(parent);rb_set_black(uncle);rb_set_red(gparent);node=gparent;continue;}//情形四if(parent->left==node){rbtree_right_rotate(root,parent);tmp=parent;parent=node;node=tmp;}//情形五rbtree_left_rotate(root,gparent);rb_set_black(parent);rb_set_red(gparent);}}rb_set_black(root->node);
}/** 添加节点:将节点(node)插入到红黑树中** 参数说明:* root 红黑树的根* node 插入的结点 // 对应《算法导论》中的z*/
static void rbtree_insert(RBRoot *root, Node *node)
{Node *y = NULL;Node *x = root->node;// 1. 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。while (x != NULL){y = x;if (node->key < x->key)x = x->left;elsex = x->right;}rb_parent(node) = y;//找到父节点并把要插入节点的父节点的指针修改//修改父节点的子节点指针if (y != NULL){if (node->key < y->key)y->left = node; // 情况2:若“node所包含的值” < “y所包含的值”,则将node设为“y的左孩子”elsey->right = node; // 情况3:(“node所包含的值” >= “y所包含的值”)将node设为“y的右孩子” }else{root->node = node; // 情况1:若y是空节点,则将node设为根}// 2. 设置节点的颜色为红色node->color = RED;// 3. 将它重新修正为一颗rb树rbtree_insert_fixup(root, node);
}/** 创建结点** 参数说明:* key 是键值。* parent 是父结点。* left 是左孩子。* right 是右孩子。*/
static Node* create_rbtree_node(Type key, Node *parent, Node *left, Node* right)
{Node* p;if ((p = (Node *)malloc(sizeof(Node))) == NULL)return NULL;p->key = key;p->left = left;p->right = right;p->parent = parent;p->color = BLACK; // 默认为黑色return p;
}/* * 新建结点(节点键值为key),并将其插入到红黑树中** 参数说明:* root 红黑树的根* key 插入结点的键值* 返回值:* 0,插入成功* -1,插入失败*/
int insert_rbtree(RBRoot *root, Type key)
{Node *node; // 新建结点// 不允许插入相同键值的节点。// (若想允许插入相同键值的节点,注释掉下面两句话即可!)if (search(root->node, key) != NULL)return -1;// 如果新建结点失败,则返回。if ((node=create_rbtree_node(key, NULL, NULL, NULL)) == NULL)return -1;rbtree_insert(root, node);return 0;
}/** 红黑树删除修正函数** 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数;* 目的是将它重新塑造成一颗红黑树。** 参数说明:* root 红黑树的根* node 待修正的节点*/
static void rbtree_delete_fixup(RBRoot *root, Node *node, Node *parent)
{Node *other;//下面的x说的是nodewhile ((!node || rb_is_black(node)) && node != root->node){if (parent->left == node){//删除other = parent->right;if (rb_is_red(other)){// Case 1: x的兄弟w是红色的,删除77 rb_set_black(other);rb_set_red(parent);rbtree_left_rotate(root, parent);other = parent->right;}if ((!other->left || rb_is_black(other->left)) &&(!other->right || rb_is_black(other->right))){// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的,删除65时,删除82时,二级进入循环rb_set_red(other);node = parent;parent = rb_parent(node);}else{if (!other->right || rb_is_black(other->right)){// Case 3: x的兄弟w是黑色的,并且w的右孩子为黑色。 rb_set_black(other->left);rb_set_red(other);rbtree_right_rotate(root, other);other = parent->right;}// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。rb_set_color(other, rb_color(parent));rb_set_black(parent);rb_set_black(other->right);rbtree_left_rotate(root, parent);node = root->node;break;}}else{//删除other = parent->left;if (rb_is_red(other)){// Case 1: x的兄弟w是红色的 rb_set_black(other);rb_set_red(parent);rbtree_right_rotate(root, parent);other = parent->left;}if ((!other->left || rb_is_black(other->left)) &&(!other->right || rb_is_black(other->right))){// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的,删除77 rb_set_red(other);node = parent;parent = rb_parent(node);}else{if (!other->left || rb_is_black(other->left)){//删除99时,应该是w的左孩子是黑色// Case 3: x的兄弟w是黑色的,并且w的左孩子是为黑色。 rb_set_black(other->right);rb_set_red(other);rbtree_left_rotate(root, other);other = parent->left;}// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。rb_set_color(other, rb_color(parent));rb_set_black(parent);rb_set_black(other->left);rbtree_right_rotate(root, parent);node = root->node;break;}}}if (node)rb_set_black(node);
}/* * 删除结点** 参数说明:* tree 红黑树的根结点* node 删除的结点*/
void rbtree_delete(RBRoot *root, Node *node)
{Node *child, *parent;int color;// 被删除节点的"左右孩子都不为空"的情况。if ( (node->left!=NULL) && (node->right!=NULL) ) {// 被删节点的后继节点。(称为"取代节点")// 用它来取代"被删节点"的位置,然后再将"被删节点"去掉。Node *replace = node;// 获取后继节点,右分支最左的结点就是我们要找的replace = replace->right;while (replace->left != NULL)replace = replace->left;// "node节点"不是根节点(只有根节点不存在父节点),开始替换if (rb_parent(node)){if (rb_parent(node)->left == node)rb_parent(node)->left = replace;elserb_parent(node)->right = replace;} else // "node节点"是根节点,更新根节点。删除60在这里root->node = replace;// child是"取代节点"的右孩子,也是需要"调整的节点"。// "取代节点"肯定不存在左孩子!因为它是一个后继节点。child = replace->right;parent = rb_parent(replace);// 保存"取代节点"的颜色color = rb_color(replace);// "被删除节点"是"它的后继节点的父节点"if (parent == node){parent = replace;} else{// child不为空if (child)rb_set_parent(child, parent);//因为结点要移到删除位,所以它的右节点,变为其父亲的左结点parent->left = child;replace->right = node->right;rb_set_parent(node->right, replace);}replace->parent = node->parent;replace->color = node->color;replace->left = node->left;node->left->parent = replace;//移除一个红色结点不需要调整,但是移除一个黑色结点,红黑树平衡就会打破if (color == BLACK)rbtree_delete_fixup(root, child, parent);free(node);return ;}//删除结点有一边是NULLif (node->left !=NULL)child = node->left;else child = node->right;//获取删除结点的父亲parent = node->parent;// 保存"取代节点"的颜色color = node->color;if (child)child->parent = parent;// "node节点"不是根节点if (parent){//在父亲的左边,就把自己孩子放左边,在右边,就把自己孩子放右边if (parent->left == node)parent->left = child;elseparent->right = child;}elseroot->node = child;//如果是根,孩子就变为根if (color == BLACK)rbtree_delete_fixup(root, child, parent);free(node);
}/* * 删除键值为key的结点** 参数说明:* tree 红黑树的根结点* key 键值*/
void delete_rbtree(RBRoot *root, Type key)
{Node *z, *node; if ((z = search(root->node, key)) != NULL)rbtree_delete(root, z);
}/** 销毁红黑树*/
static void rbtree_destroy(RBTree tree)
{if (tree==NULL)return ;if (tree->left != NULL)rbtree_destroy(tree->left);if (tree->right != NULL)rbtree_destroy(tree->right);free(tree);
}void destroy_rbtree(RBRoot *root)
{if (root != NULL)rbtree_destroy(root->node);free(root);
}/** 打印"红黑树"** tree -- 红黑树的节点* key -- 节点的键值 * direction -- 0,表示该节点是根节点;* -1,表示该节点是它的父结点的左孩子;* 1,表示该节点是它的父结点的右孩子。*/
static void rbtree_print(RBTree tree, Type key, int direction)
{if(tree != NULL){if(direction==0) // tree是根节点printf("%2d(B) is root\n", tree->key);else // tree是分支节点printf("%2d(%s) is %2d's %6s child\n", tree->key, rb_is_red(tree)?"R":"B", key, direction==1?"right" : "left");rbtree_print(tree->left, tree->key, -1);rbtree_print(tree->right,tree->key, 1);}
}void print_rbtree(RBRoot *root)
{if (root!=NULL && root->node!=NULL)rbtree_print(root->node, root->node->key, 0);
}/*** C语言实现的红黑树(Red Black Tree)** @author skywang* @date 2013/11/18*/#define CHECK_INSERT 1 // "插入"动作的检测开关(0,关闭;1,打开)
#define CHECK_DELETE 1 // "删除"动作的检测开关(0,关闭;1,打开)
#define LENGTH(a) ( (sizeof(a)) / (sizeof(a[0])) )void main()
{int a[] = {10, 40, 30, 60, 90, 70, 20, 50, 80,65};//int a[] = {10, 40, 30, 60, 90, 70, 20, 50, 80,65,66,45,77,99,82,23,55,88,33,47};int i, ilen=LENGTH(a);RBRoot *root=NULL;root = create_rbtree();//给指针申请对应的结构体空间printf("== 原始数据: ");for(i=0; i<ilen; i++)printf("%d ", a[i]);printf("\n");for(i=0; i<ilen; i++){insert_rbtree(root, a[i]);
#if CHECK_INSERTprintf("== 添加节点: %d\n", a[i]);printf("== 树的详细信息: \n");print_rbtree(root);printf("\n");
#endif}printf("== 前序遍历: ");preorder_rbtree(root);printf("\n== 中序遍历: ");inorder_rbtree(root);printf("\n== 后序遍历: ");postorder_rbtree(root);printf("\n");if (rbtree_minimum(root, &i)==0)printf("== 最小值: %d\n", i);if (rbtree_maximum(root, &i)==0)printf("== 最大值: %d\n", i);printf("== 树的详细信息: \n");print_rbtree(root);printf("\n");#if CHECK_DELETEfor(i=0; i<ilen; i++){printf("== 删除节点: %d\n", a[i]);delete_rbtree(root, a[i]);if (root){printf("== 树的详细信息: \n");print_rbtree(root);printf("\n");}}
#endifdestroy_rbtree(root);
}
相关文章:

补档:红黑树代码实现+简略讲解
红黑树讲解和实现1 红黑树介绍1.1 红黑树特性1.2 红黑树的插入1.3 红黑树的删除2 完整代码实现2.1 rtbtree.h头文件2.2 main.c源文件1 红黑树介绍 红黑树( Red-Black tree,简称RB树)是一种自平衡二叉查找树,是计算机科学中常见的一种数据结构,…...
FirePower X2 14.0.1 for RAD Studio Alexandria
介绍 FirePower X2 FirePower X2 集成了 RAD Studio 11.0 Alexandria 中的新功能,并预览了我们的新特色组件 TwwDataGrouper。 FirePower X2 还允许您为 Apple 的新 M1 芯片构建应用程序,这样您就可以进一步利用 M1 芯片来提高本机应用程序的性能&#x…...
)
二十九、MongoDB 恢复数据( mongorestore )
MongoDB mongorestore 脚本命令可以用来恢复备份的数据 语法 MongoDB mongorestore 命令脚本语法如下 $ mongorestore -h <hostname><:port> -d dbname <path> 参数说明 -h <:port>, -h<:port> MongoDB 所在服务器地址,默认为 l…...

【数据分析】缺失数据如何处理?pandas
本文目录1. 基础概念1.1. 缺失值分类1.2. 缺失值处理方法2. 缺失观测及其类型2.1. 了解缺失信息2.2. 三种缺失符号2.3. Nullable类型与NA符号2.4. NA的特性2.5. convert_dtypes方法3. 缺失数据的运算与分组 3.1. 加号与乘号规则3.2. groupby方法中的缺失值4. 填充与剔除4.1. fi…...
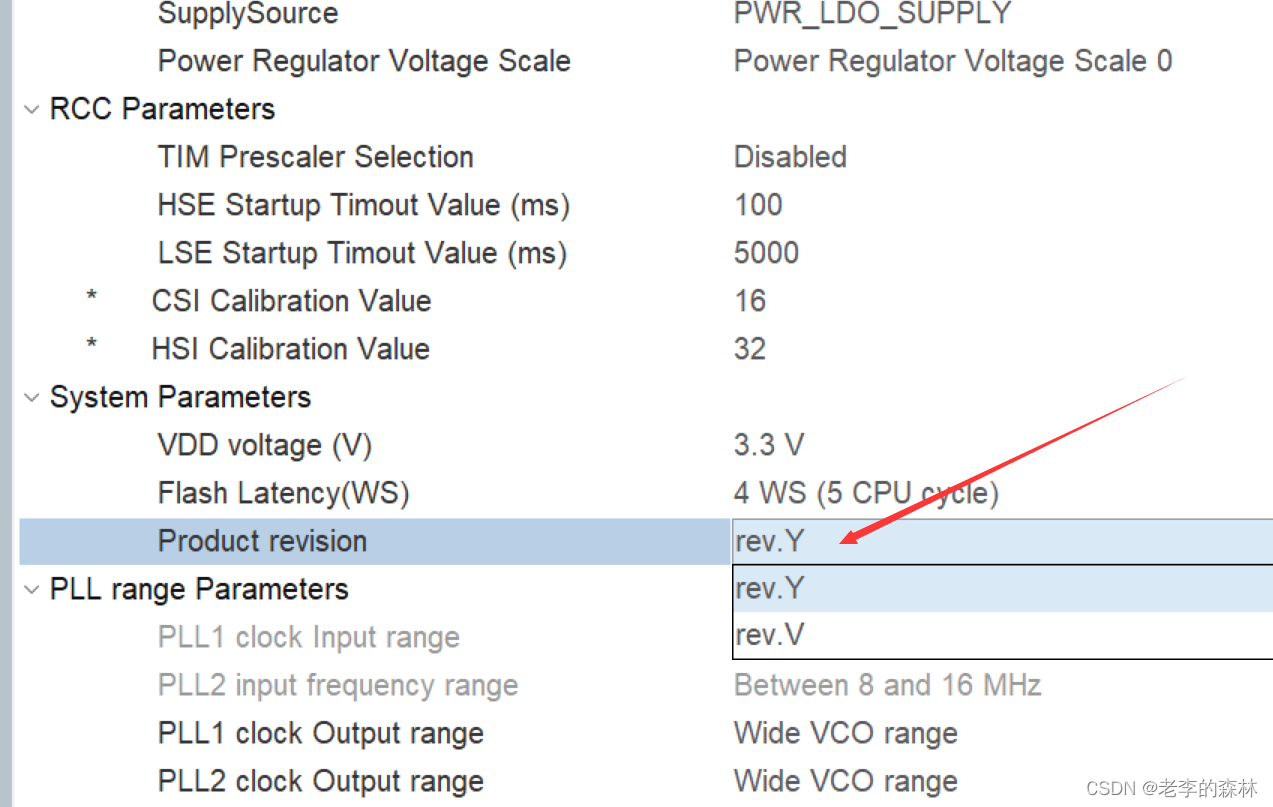
嵌入式开发--STM32H750VBT6开发中,新版本CubeMX的时钟问题,不能设置到最高速度480MHZ
嵌入式开发–STM32H750VBT6开发中,新版本CubeMX的时钟问题,不能设置到最高速度480MHZ 问题描述 之前开发的项目,开发环境是CubeMX6.6.1,H7系列的支持包版本是1.10.0。跑得没问题,最近需要对项目做修改,同…...

一文读懂PaddleSpeech中英混合语音识别技术
语音识别技术能够让计算机理解人类的语音,从而支持多种语音交互的场景,如手机应用、人车协同、机器人对话、语音转写等。然而,在这些场景中,语音识别的输入并不总是单一的语言,有时会出现多语言混合的情况。例如&#…...

问题三十四:傅立叶变换——高通滤波
高通滤波器是一种可以通过去除图像低频信息来增强高频信息的滤波器。在图像处理中,高通滤波器常常用于去除模糊或平滑效果,以及增强边缘或细节。在本篇回答中,我们将使用Python和OpenCV实现高通滤波器。 Step 1:加载图像并进行傅…...
)
flink 键控状态(keyed state)
github开源项目flink-note的笔记。本博客的实现代码都写在项目的flink-state/src/main/java/state/keyed/KeyedStateDemo.java文件中。 项目github地址: github 1. flink键控状态 flink键控状态是作用与flink KeyedStream上的,也就是说需要将DataStream先进行keyby之后才能使…...
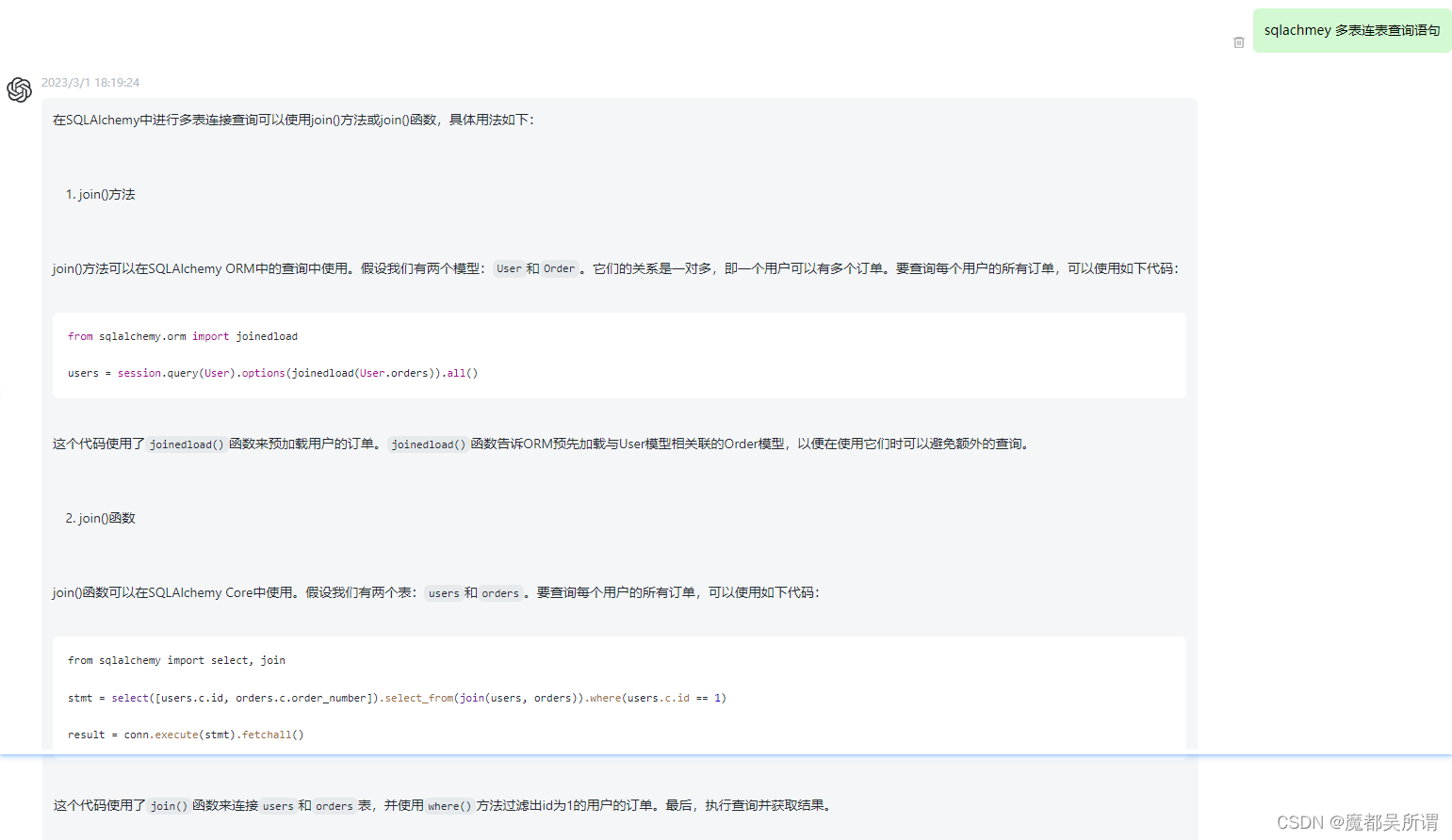
【ChatGPT】sqlachmey 多表连表查询语句
感受下科技带来的魅力,这篇文章是通过ChatGPT自动生成的,不得不说技术强大!!! 在SQLAlchemy中进行多表连接查询可以使用join()方法或join()函数,具体用法如下: join()方法 join()方法可以在SQLAlchemy ORM中的查询中使用。假设…...

win11 系统登录问题,PIN 设置问题
我的电脑配置是华为MateBook X Pro 12,i7处理器,16G,1T,win11 系统通过微软账户登录,下午一直登录不进去,网络能连外网,分析应该是连微软服务器不行。连续登录几十次,偶尔可能有一次…...
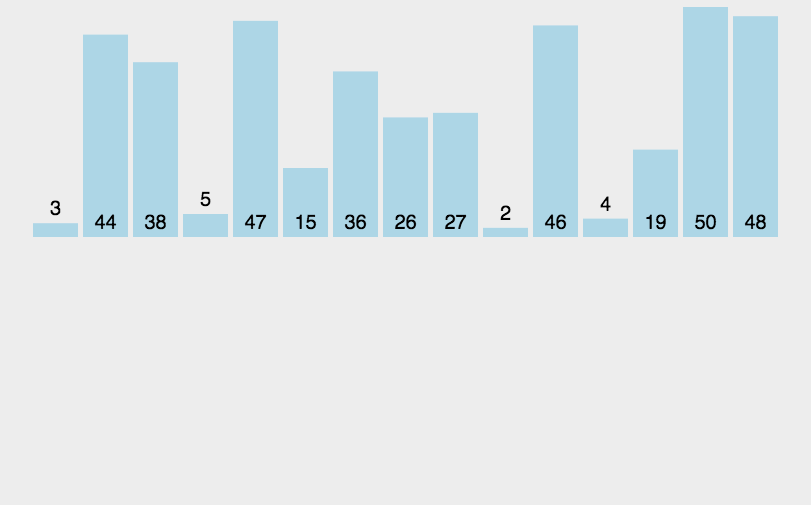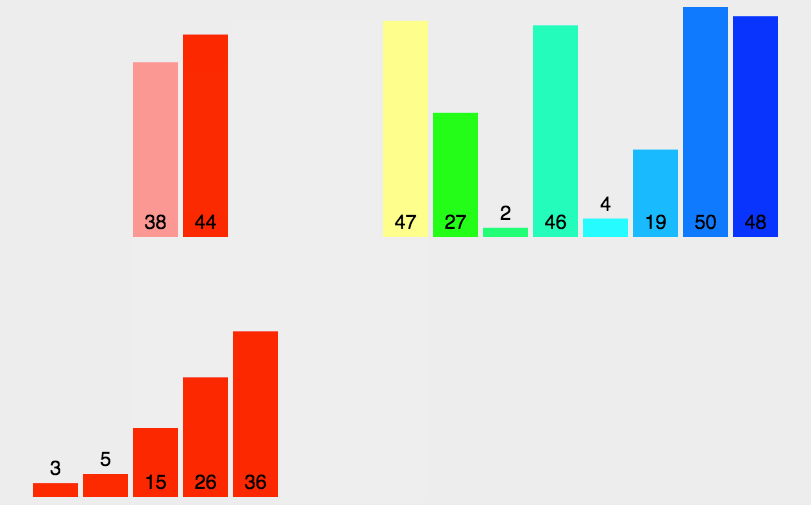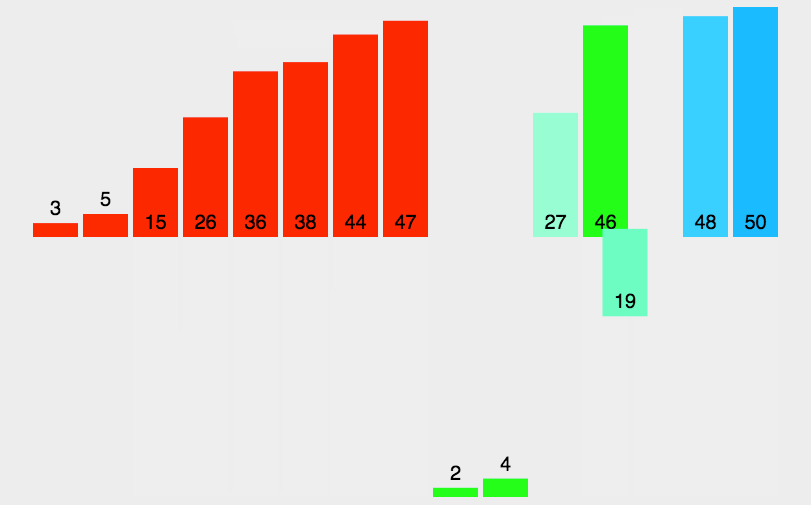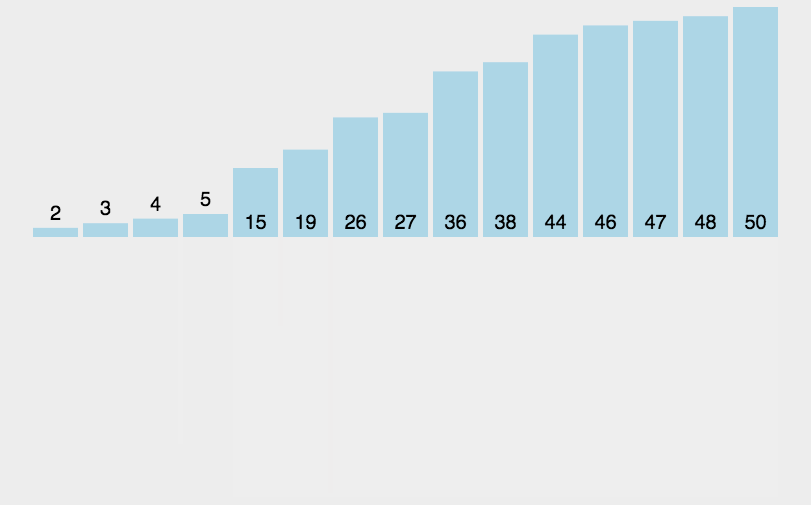
数据结构六大排序
1.插入排序 思路: 从第一个元素开始认为是有序的,去一个元素tem从有序序列从后往前扫描,如果该元素大于tem,将该元素一刀下一位,循环步骤3知道找到有序序列中小于等于的元素将tem插入到该元素后,如果已排序…...

快速生成QR码的方法:教你变成QR Code Master
目录 简介: 具体实现步骤: 一、可以使用Python中的qrcode和tkinter模块来生成QR码。以下是一个简单的例子,演示如何在Tkinter窗口中获取用户输入并使用qrcode生成QR码。 1)首先需要安装qrcode模块,可以使用以下命令在终端或命令…...

tensorflow1.14.0安装教程--保姆级
//方法不止一种,下面仅展示一种。 注:本人电脑为win11,anaconda的python版本为3.9,但tensorflow需要python版本为3.7,所以下面主要阐述将python版本改为3.7后的安装过程以及常遇到的问题。 1.首先电脑安装好anaconda…...

AcWing算法提高课-3.1.3香甜的黄油
宣传一下算法提高课整理 <— CSDN个人主页:更好的阅读体验 <— 题目传送门点这里 题目描述 农夫John发现了做出全威斯康辛州最甜的黄油的方法:糖。 把糖放在一片牧场上,他知道 N 只奶牛会过来舔它,这样就能做出能卖好价…...

私库搭建1:Nexus 安装 Docker 版
本文内容以语雀为准 文档 https://hub.docker.com/r/sonatype/nexus3Docker 安装:https://www.yuque.com/xuxiaowei-com-cn/gitlab-k8s/docker-install 安装 创建文件夹 由于 Nexus 的数据可能会很大,比如:作为 Docker、Maven 私库时&…...

LeetCode-面试题 05.02. 二进制数转字符串【数学,字符串,位运算】
LeetCode-面试题 05.02. 二进制数转字符串【数学,字符串,位运算】题目描述:解题思路一:简单暴力。小数点后面的二进制,now首先从0.5开始之和每次除以2。然后依次判断当前数是否大于now,是则答案加1。若等于…...
pandas: 三种算法实现递归分析Excel中各列相关性
目录 前言 目的 思路 代码实现 1. 循环遍历整个SDGs列,两两拿到数据 2. 调用pandas库函数直接进行分析 完整源码 运行效果 总结 前言 博主之前刚刚被学弟邀请参与了2023美赛,这也是第一次正式接触数学建模竞赛,现在已经提交等待结果…...

【Python百日进阶-Web开发-Vue3】Day543 - Vue3 商城后台 03:登录页面初建
文章目录 一、创建登录页面 login.vue二、登录页面响应式处理,以适应不同大小的屏幕2.1 element-plus 的layout布局中关于响应式的说明2.2 修改login.vue文件2.2.1 :lg=16 大于1200px 横排 2:12.2.2 :md=12 大于992小于1200px 横排 1:12.2.3 小于992 竖排三、引入Element-plus…...
python画直方图,刻画数据分布
先展示效果 准备一维数据 n 个数据元素计算最大值,最小值、均值、标准差、以及直方图分组 import numpy as np data list() for i in range(640):data.append(np.random.normal(1)) print(data)z np.histogram(data, bins64) print(list(z[0])) ### 对应 x 轴数据…...
【学数学关键是要学会在什么情况下,知道使用什么工具。】)
几何学小课堂:非欧几何(广义相对论采用黎曼几何作为数学工具)【学数学关键是要学会在什么情况下,知道使用什么工具。】
文章目录 引言I 非欧几何1.1 黎曼几何1.2 共形几何1.3 罗氏几何II 黎曼几何的应用2.1 广义相对论2.2 超弦III 理解不同的几何体系的共存3.1 更扎实的欧氏几何3.2 殊途同归引言 公理有错会得到两种情况: 如果某一条自己设定的新公理和现有的公理相矛盾,那么相应的知识体系就建…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
